1.为什么我们需要红黑树?
在开始深入红黑树之前,我们先来思考一个问题:为什么普通的 二叉搜索树(Binary Search Tree, BST) 还不够好?
一个理想的BST,每次插入和查找都能将问题规模减半,其操作的时间复杂度是 O(log n)。但BST有一个致命的弱点:它对插入数据的顺序非常敏感。如果插入一个有序序列(例如 1, 2, 3, 4, 5),BST会退化成一个 链表。
在这种情况下,所有的操作(查找、插入、删除)的时间复杂度都会恶化到 O(n),这与我们使用树形结构的初衷背道而驰。
为了解决这个问题,平衡二叉搜索树(Balanced BST) 应运而生。它的核心思想是:在每次插入或删除节点后,通过一系列的调整操作,确保树始终保持一个“大致平衡”的状态,从而将树的高度维持在 O(log n) 级别。
红黑树(Red-Black Tree, RBT) 就是其中最著名和应用最广泛的一种。它不是一种“绝对平衡”的树(比如AVL树),而是一种“弱平衡”或“大致平衡”的树。它通过引入颜色属性和几条简单的规则,在维护平衡和调整成本之间取得了绝佳的折衷。在C++ STL中,我们熟知的 std::map, std::set, std::multimap, std::multiset 等关联式容器,其底层实现正是红黑树。
2.红黑树的规则
1.每个节点要么是红色,要么是黑色。
2.根节点一直是黑色。
3.如果一个节点是红色的,那么它的子节点必须是黑色的。
4.从任意节点到每个叶子节点的路径必须包含相同的黑色节点。
正是这四条规则,共同确保了红黑树中最长路径不会超过最短路径的两倍,从而保证了其 O(log n) 的时间复杂度。
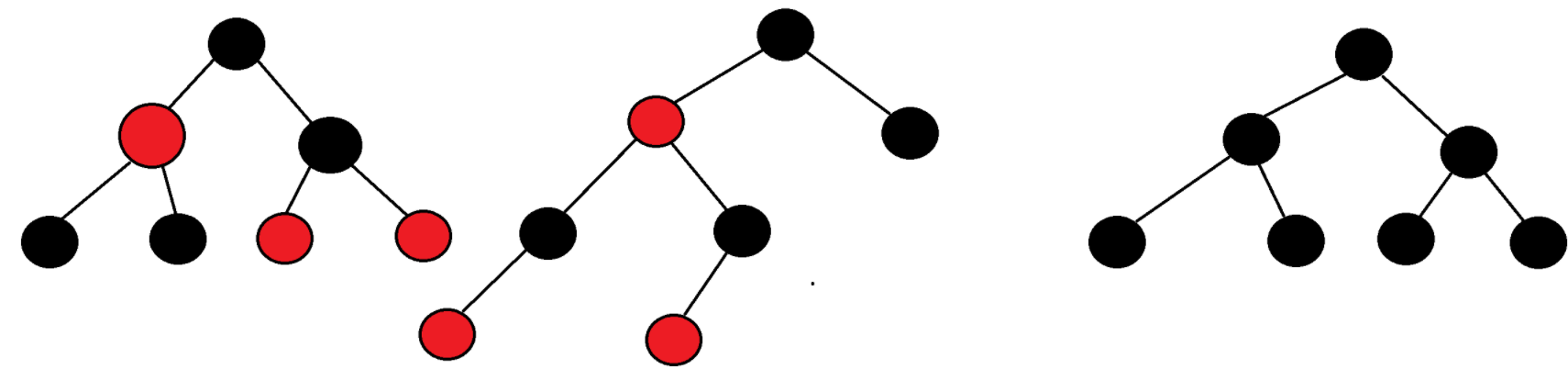
下图三种示例都符合红黑树规则:
3.红黑树的实现
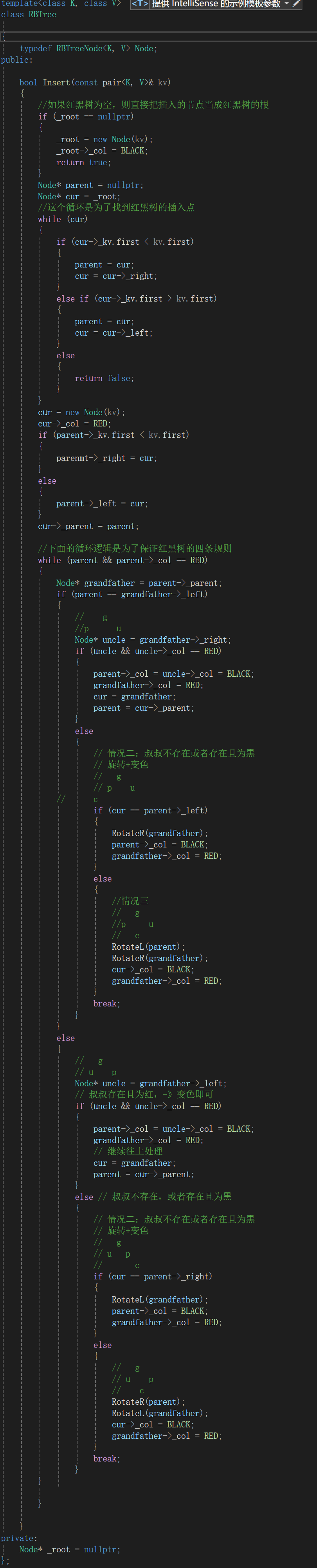
3.1 红⿊树树插⼊⼀个值的⼤概过程
1. 插⼊⼀个值按⼆叉搜索树规则进⾏插⼊,插⼊后我们只需要观察是否符合红⿊树的4条规则。
2. 如果是空树插⼊,新增结点是⿊⾊结点。如果是⾮空树插⼊,新增结点必须红⾊结点,因为⾮空树插⼊,新增⿊⾊结点就破坏了规则4,规则4是很难维护的。
3. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是⿊⾊的,则没有违反任何规则,插⼊结束
4. ⾮空树插⼊后,新增结点必须红⾊结点,如果⽗亲结点是红⾊的,则违反规则3。进⼀步分析,c是 红⾊,p为红,g必为⿊,这三个颜⾊都固定了,关键的变化看u的情况,需要根据u分为以下⼏种 情况分别处理。
说明:下图中假设我们把新增结点标识为c (cur),c的⽗亲标识为p(parent),p的⽗亲标识为
g(grandfather),p的兄弟标识为u(uncle)
解释一下为什么新增节点必须为红色:
1 . 如果新增节点是黑色的话,就破坏了规则4
2. 如果新增节点是红色的话,就有两种情况:如果父节点是黑色,那么这个插入就是符合规则的,如果父节点是红色,我们就需要考虑下面的情况,视情况变色或者旋转。
3.2 红黑树的结构
为了更好的了解红黑树的旋转和变色情况,我们先来了解一下红黑树的结构:

3.3 旋转和变色(重点!!!)
当我插入一个红色的节点,我们在特定情况下,要把红黑树进行旋转或者变色,主要为了保证红黑树的结构,符合4大规则,一共有三种情况需要我们来做出改变,下面我会详细介绍每一种情况:
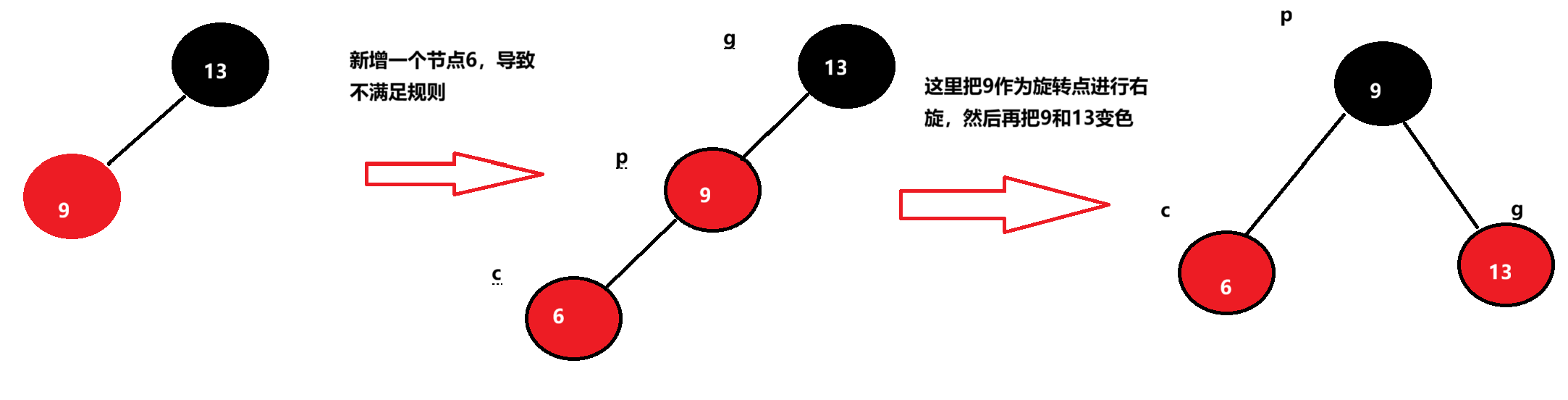
3.3.1 只变色
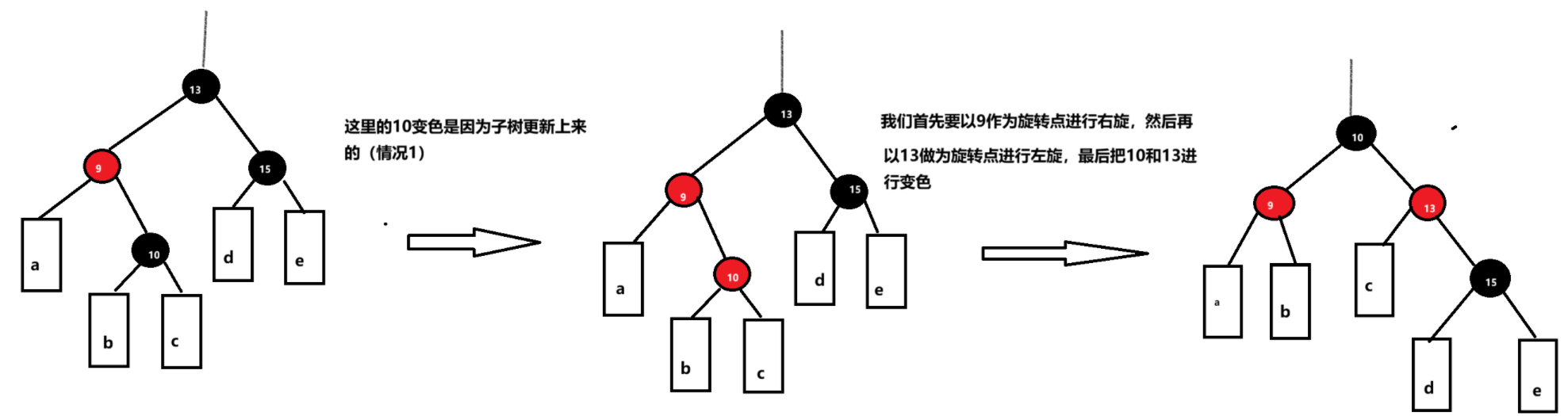
下面情况不满足条件三,所以我们需要把u和p变为黑色,把g变为红色,然后把g当成新的c,继续向上,直到满足所有规则。
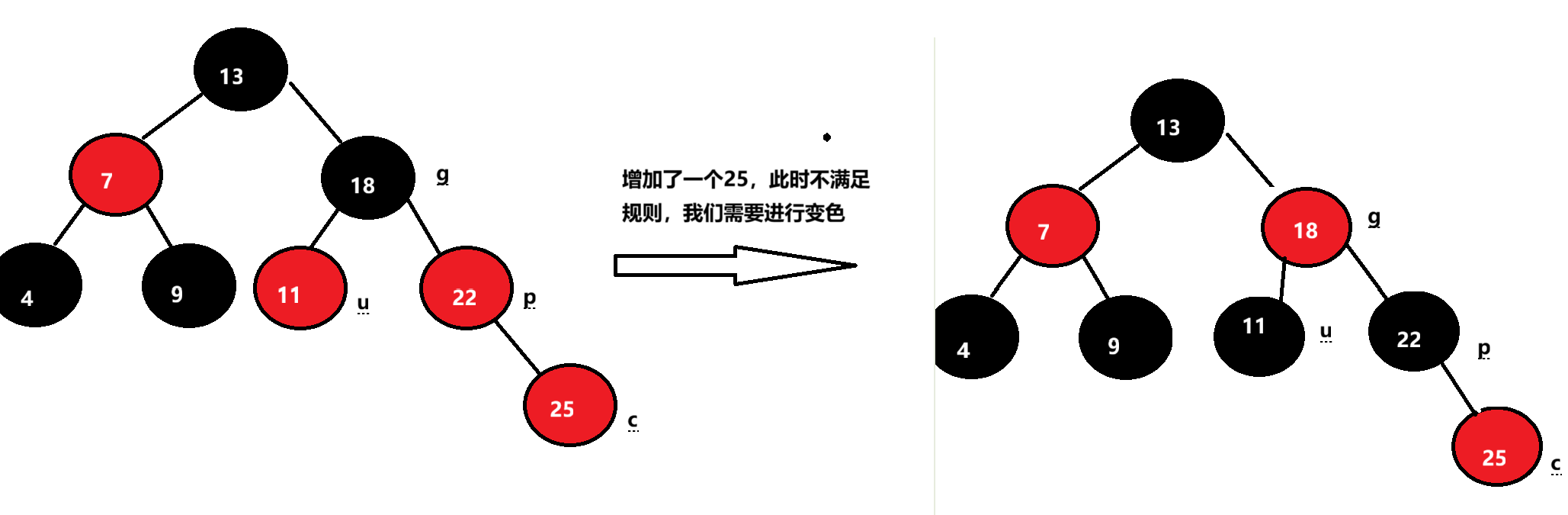
上图是一个具体的情况,其实很多时候,我们需要向上更新多次,才能达到满足规则的效果,下面展示一下抽象的示例:

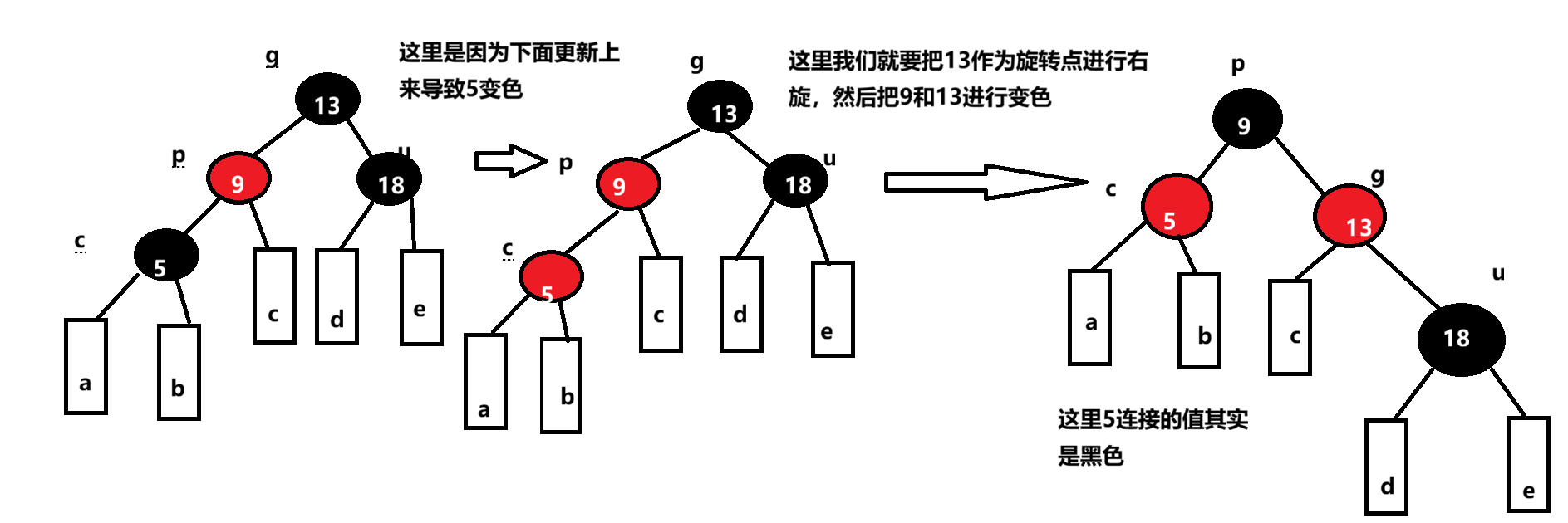
3.3.2 变色加单旋
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点,u存在且为⿊,则 c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上来的。(符合下面的情况都按这个规则进行变色加旋转,前提是颜色符合上述)
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解决问题,需要旋转+变⾊。
下面是实际图:
u不存在:
u存在且为黑:
注意:需要把下面连接的长方体想象成一个大的子树,每个图片都可以想象成一颗子树
旋转完后c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且
不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。
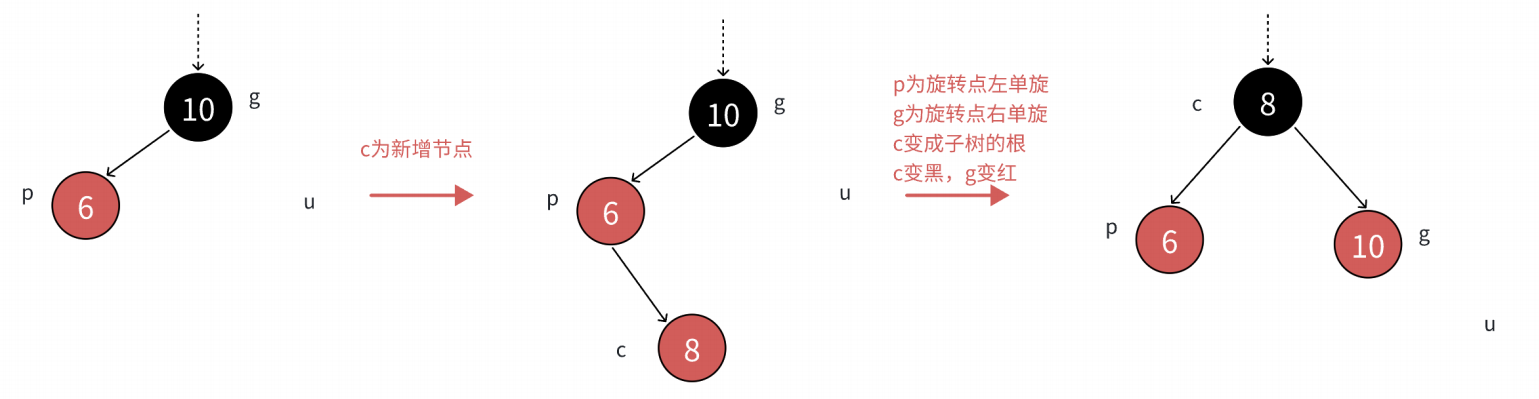
3.3.3 双旋加变色:
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点,u存在且为⿊,则 c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上来的。
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解决问题,需要旋转+变⾊。
u不存在的情况:
u存在且为黑:
旋转完后c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且
不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。
3.4 红黑树的插入代码实现
注意:这里面的左旋函数和右旋函数在AVL里面有相似实现,这里我就不一一截图了。
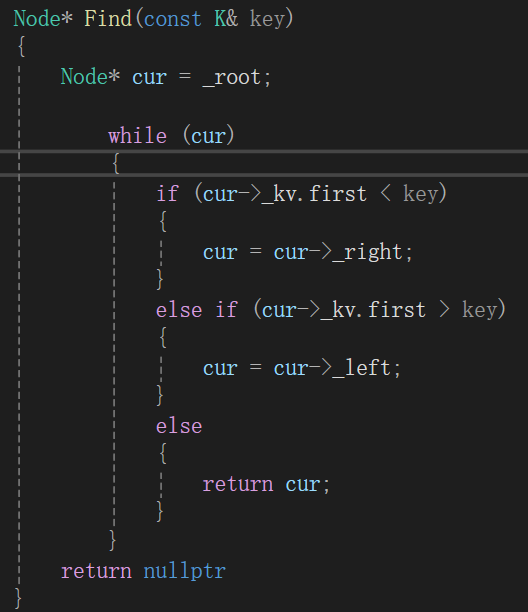
4. 红⿊树的查找
按⼆叉搜索树逻辑实现即可,搜索效率为 O(logN)
5.红黑树的验证
这⾥获取最⻓路径和最短路径,检查最⻓路径不超过最短路径的2倍是不可⾏的,因为就算满⾜这个条件,红⿊树也可能颜⾊不满⾜规则,当前暂时没出问题,后续继续插⼊还是会出问题的。所以我们还是去检查4点规则,满⾜这4点规则,⼀定能保证最⻓路径不超过最短路径的2倍。
1. 规则1枚举颜⾊类型,天然实现保证了颜⾊不是⿊⾊就是红⾊。
2. 规则2直接检查根即可
3. 规则3前序遍历检查,遇到红⾊结点查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲的颜⾊就⽅便多了。
4. 规则4前序遍历,遍历过程中⽤形参记录跟到当前结点的blackNum(⿊⾊结点数量),前序遍历遇到⿊⾊结点就++blackNum,⾛到空就计算出了⼀条路径的⿊⾊结点数量。再任意⼀条路径⿊⾊结点数量作为参考值,依次⽐较即可。
总结:
红黑树是 “工程化的平衡 BST”:它没有 AVL 树那么 “严格”,但更贴近实际开发的需求;它的核心是 5 条颜色特性,所有操作都是对这些特性的维护;它的价值不在于 “理论最优”,而在于 “实战高效”—— 这也是它能成为底层开发 “万金油” 数据结构的根本原因。