[信号与系统个人笔记]第三章 连续时间信号与系统的频域分析 Part 4
- 2025.8.31
- 3.1 连续时间周期信号的傅里叶级数
- 2025.9.1
- 3.2 连续时间周期信号的频谱分析
- 2025.9.2
- 3.3 连续时间信号的傅里叶变换 part1
- 2025.9.3
- 3.3 连续时间信号的傅里叶变换 part2
- 2025.9.9
- 3.4 傅里叶变换的性质 I
- 2025.9.14
- 3.4 傅里叶变换的性质 ll
- 2025.9.18
- 3.4 傅里叶变换的性质 III
- 3.4* 信号的能量谱与功率谱
- 2025.9.29
- 3.5 周期信号的傅里叶变换
- 3.6 抽样定理
3.5 周期信号的傅里叶变换
一般周期信号的傅里叶变换
周期为TTT的周期信号可以展开为指数形式的傅里叶级数:
fT(t)=∑n=−∞+∞FnejnΩt,Ω=2πTF[fT(t)]=F[∑n=−∞+∞FnejnΩt]
\begin{align}
&f_{T}(t)=\sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t},\Omega=\frac{2\pi}{T}\\ \\
&\mathcal{F}[f_{T}(t)]=\mathcal{F}\left[ \sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t} \right]
\end{align}
fT(t)=n=−∞∑+∞FnejnΩt,Ω=T2πF[fT(t)]=F[n=−∞∑+∞FnejnΩt]
而FnF_{n}Fn与ttt无关,因此:
F[fT(t)]=∑n=−∞+∞FnF[ejnΩt]而1↔2πδ(ω) ⟹ ejnΩ↔2πδ(ω−nΩ)
\begin{align}
&\mathcal{F}[f_{T}(t)]=\sum_{n=-\infty}^{+\infty}F_{n}\mathcal{F}[e^{jn\Omega t}]\\ \\
&而1\leftrightarrow 2\pi \delta(\omega)\\ \\
&\implies e^{jn\Omega}\leftrightarrow 2\pi \delta(\omega-n\Omega)
\end{align}
F[fT(t)]=n=−∞∑+∞FnF[ejnΩt]而1↔2πδ(ω)⟹ejnΩ↔2πδ(ω−nΩ)
一般周期信号的傅里叶变换:
F[ft(t)]=2π∑nm=−∞+∞Fnδ(ω−nΩ),Ω=2πT
\begin{align}
&\mathcal{F}[f_{t}(t)]=2\pi \sum_{nm=-\infty }^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega= \frac{2\pi}{T}
\end{align}
F[ft(t)]=2πnm=−∞∑+∞Fnδ(ω−nΩ),Ω=T2π
- 周期信号的频谱密度由冲激序列组成
- 冲激位置:ω=nΩ\omega=n\Omegaω=nΩ,谐波频率处
- 冲激强度:2πFn2\pi F_{n}2πFn由傅里叶系数确定
例
求周期冲激序列δT(t)=∑n=−∞+∞δ(t−nT)\delta_{T}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)δT(t)=∑n=−∞+∞δ(t−nT)的傅里叶变换
Fn=1T∫−T2T2δT(t)e−jnΩtdt=1T[e−jnΩt]∣t=0=1T而fT(t)↔2π∑n=−∞+∞δ(t−nT)δT(t)↔2π∑n=−∞+∞Fnδ(ω−nΩ)=2πT∑n=−∞+∞δ(ω−nΩ)=ΩδΩ(ω)
\begin{align}
&F_{n}= \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}\delta_{T}(t)e^{-jn\Omega t}dt=\frac{1}{T}[e^{-jn\Omega t}]\bigg|_{t=0}=\frac{1}{T}\\ \\
&而f_{T}(t)\leftrightarrow 2\pi \sum_{n=-\infty}^{+\infty}\delta(t-nT) \\ \\
&\delta_{T}(t)\leftrightarrow 2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega)= \frac{2\pi}{T}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)=\Omega \delta_{\Omega}(\omega)
\end{align}
Fn=T1∫−2T2TδT(t)e−jnΩtdt=T1[e−jnΩt]t=0=T1而fT(t)↔2πn=−∞∑+∞δ(t−nT)δT(t)↔2πn=−∞∑+∞Fnδ(ω−nΩ)=T2πn=−∞∑+∞δ(ω−nΩ)=ΩδΩ(ω)
结论:
δT(t)=∑n=−∞+∞δ(t−nT)↔Ω∑n=−∞+∞δ(ω−nΩ)=ΩδΩ(ω),Ω=2πT
\delta_{T}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT) \leftrightarrow \Omega \sum_{n=-\infty }^{+\infty}\delta(\omega-n\Omega)=\Omega \delta_{\Omega}(\omega),\Omega=\frac{2\pi}{T}
δT(t)=n=−∞∑+∞δ(t−nT)↔Ωn=−∞∑+∞δ(ω−nΩ)=ΩδΩ(ω),Ω=T2π
周期信号傅里叶系数与傅里叶变化的关系
任意周期为TTT的周期信号fT(t)f_{T}(t)fT(t)可以表示为第一个周期内的脉冲信号f0(t)f_{0}(t)f0(t)和周期冲激序列卷积的结果
ft(t)=f0(t)∗δT(t)=f0(t)∗∑n=−∞+∞δ(t−nT)F(jω)=F0(jω)⋅Ω∑n=−∞+∞δ(ω−nΩ)=Ω∑n=−∞+∞δ(ω−nΩ)=Ω∑n=−∞+∞F0(jmΩ)δ(ω−nΩ)而F(jω)=2π∑n=−∞+∞Fnδ(ω−nΩ) ⟹ 2πFn=ΩF0(jnΩ) ⟹ Fn=1TF0(jnΩ)=1TF0(jω)∣ω=nΩ
\begin{align}
&f_{t}(t)=f_{0}(t)*\delta_{T}(t)=f_{0}(t)*\sum_{n=-\infty}^{+\infty}\delta(t-nT)\\ \\
&F(j\omega)=F_{0}(j\omega)\cdot \Omega \sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)=\Omega \sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega)\\ \\
&=\Omega \sum_{n=-\infty}^{+\infty}F_{0}(jm\Omega)\delta(\omega-n\Omega)\\ \\
&而F(j\omega)=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega)\\ \\
&\implies 2\pi F_{n}=\Omega F_{0}(jn\Omega)\implies F_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}
\end{align}
ft(t)=f0(t)∗δT(t)=f0(t)∗n=−∞∑+∞δ(t−nT)F(jω)=F0(jω)⋅Ωn=−∞∑+∞δ(ω−nΩ)=Ωn=−∞∑+∞δ(ω−nΩ)=Ωn=−∞∑+∞F0(jmΩ)δ(ω−nΩ)而F(jω)=2πn=−∞∑+∞Fnδ(ω−nΩ)⟹2πFn=ΩF0(jnΩ)⟹Fn=T1F0(jnΩ)=T1F0(jω)ω=nΩ
求解周期信号傅里叶变换的方法
F[fT(t)]=2π∑n=−∞+∞Fnδ(ω−nΩ),Ω=2πTFn=1TF0(jnΩ)=1TF0(jω)∣ω=nΩ \begin{align} &\mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega=\frac{2\pi}{T}\\ \\ &F_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega} \end{align} F[fT(t)]=2πn=−∞∑+∞Fnδ(ω−nΩ),Ω=T2πFn=T1F0(jnΩ)=T1F0(jω)ω=nΩ
- 找周期信号在第一个周期内的单体f0(t)f_{0}(t)f0(t)
- 求f0(t)f_{0}(t)f0(t)对应的傅里叶变换F0(jω)F_{0}(j\omega)F0(jω)
- 周期信号的傅里叶系数为Fn=1TF0(jnΩ)=1TF0(jω)∣ω=nΩF_{n}=\frac{1}{T}F_{0}(jn\Omega)=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}Fn=T1F0(jnΩ)=T1F0(jω)ω=nΩ
- 周期信号的傅里叶变换F[fT(t)]=2π∑n=−∞+∞Fnδ(ω−nΩ),Ω=2πT\mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega-n\Omega),\Omega=\frac{2\pi}{T}F[fT(t)]=2π∑n=−∞+∞Fnδ(ω−nΩ),Ω=T2π
例
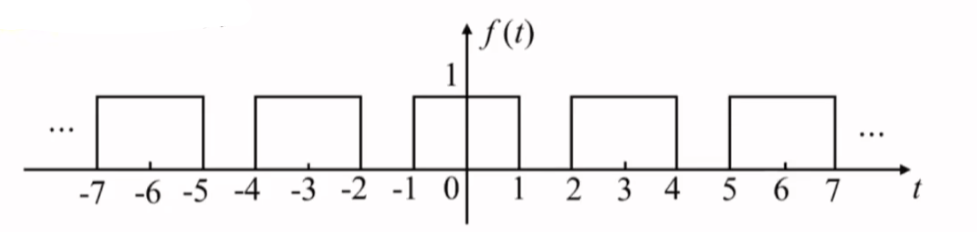
已知周期举行脉冲信号如图所示,求此信号的傅里叶变换与指数形式的傅里叶级数
f0(t)=g2(t), T=3, Ω=2πT=2π3f0(t)↔2Sa(ω)=F0(jω)Fn=1TF0(jω)∣ω=nΩ=23Sa(2π3n)∴F[fT(t)]=2π∑n=−∞+∞Fnδ(ω−nΩ)=4π3∑n=−∞+∞Sa(2π3n)⋅δ(ω−2π3n)∴f(t)=∑n=−∞+∞FnejnΩt=23∑n=−∞+∞Sa(2π3n)ej2π3nt
\begin{align}
&f_{0}(t)=g_{2}(t),\ T=3,\ \Omega=\frac{2\pi}{T}= \frac{2\pi}{3}\\ \\
&f_{0}(t)\leftrightarrow 2Sa(\omega)=F_{0}(j\omega)\\ \\
&F_{n}=\frac{1}{T}F_{0}(j\omega)\bigg|_{\omega=n\Omega}=\frac{2}{3}Sa\left( \frac{2\pi}{3}n \right)\\ \\
&\therefore \mathcal{F}[f_{T}(t)]=2\pi \sum_{n=-\infty}^{+\infty}F_{n}\delta(\omega- n\Omega)\\ \\
&=\frac{4\pi}{3}\sum_{n=-\infty}^{{+\infty}}Sa\left( \frac{2\pi}{3}n \right)\cdot \delta\left( \omega-\frac{2\pi}{3}n \right)\\ \\
&\therefore f(t)=\sum_{n=-\infty}^{+\infty}F_{n}e^{jn\Omega t}=\frac{2}{3}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{2\pi}{3}n \right)e^{j \frac{2\pi}{3}nt}
\end{align}
f0(t)=g2(t), T=3, Ω=T2π=32πf0(t)↔2Sa(ω)=F0(jω)Fn=T1F0(jω)ω=nΩ=32Sa(32πn)∴F[fT(t)]=2πn=−∞∑+∞Fnδ(ω−nΩ)=34πn=−∞∑+∞Sa(32πn)⋅δ(ω−32πn)∴f(t)=n=−∞∑+∞FnejnΩt=32n=−∞∑+∞Sa(32πn)ej32πnt
- 注意f0(t)f_{0}(t)f0(t)的定义域不一定要从原点开始取
- 将周期函数展开为傅里叶级数多了一种新思路:求基波信号的傅里叶变换,再求原函数的傅里叶级数系数,从而得到傅里叶级数
3.6 抽样定理
理想抽样及其信号的频谱
抽样的概念
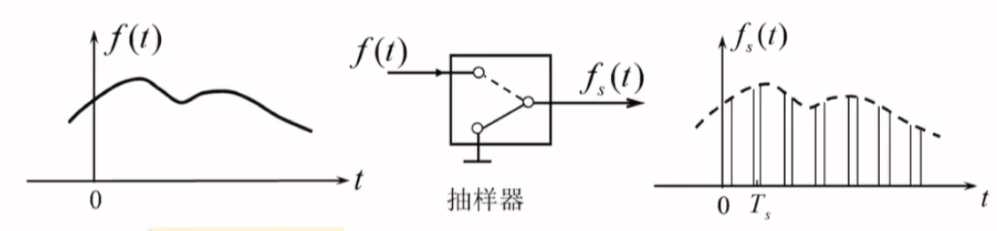
抽样可以将模拟信号转化为一系列事件离散的样值信号。实际中多采用均匀抽样,抽样间隔TsT_{s}Ts即为抽样周期,fs=1Tf_{s}=\frac{1}{T}fs=T1称为抽样频率
fs(t)=f(t)⋅s(t)
f_{s}(t)=f(t)\cdot s(t)
fs(t)=f(t)⋅s(t)
理想抽样信号及其频谱
冲激脉冲序列:s(t)=δTs(t)=∑n=−∞+∞δ(t−nTs)理想抽样信号:fs(t)=f(t)⋅δT(t)=f(t)⋅∑n=−∞+∞δ(t−nTs)=∑n=−∞+∞f(nTs)δ(t−nTs) \begin{align} 冲激脉冲序列:s(t)&=\delta_{T_{s}}(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\\ \\ 理想抽样信号:f_{s}(t)&=f(t)\cdot \delta_{T}(t)=f(t)\cdot \sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\\ \\ &=\sum_{n=-\infty} ^{+\infty}f(nT_{s})\delta(t-nT_{s})\end{align} 冲激脉冲序列:s(t)理想抽样信号:fs(t)=δTs(t)=n=−∞∑+∞δ(t−nTs)=f(t)⋅δT(t)=f(t)⋅n=−∞∑+∞δ(t−nTs)=n=−∞∑+∞f(nTs)δ(t−nTs)
- 理想抽样信号由一个个冲激信号组成
s(t)=∑n=−∞+∞δ(t−nTs)↔S(jω)=Ωs∑n=−∞+∞δ(ω−nΩs),Ωs=2πTsfs(t)=f(t)⋅s(t)↔Fs(jω)=12πF(jω)∗S(jω)=12πF(jω)∗Ωs∑n=−∞+∞δ(ω−nΩs)=1Ts∑n=−∞+∞F[j(ω−nΩs)]
\begin{align}
s(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})\leftrightarrow S(j\omega)&=\Omega_{s}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega_{s}),\Omega_{s}=\frac{2\pi}{T_{s}}\\ \\
f_{s}(t)=f(t)\cdot s(t)\leftrightarrow F_{s}(j\omega)&=\frac{1}{2\pi}F(j\omega)*S(j\omega)\\ \\
&=\frac{1}{2\pi}F(j\omega)*\Omega_{s}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\Omega_{s})\\ \\
&=\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}F[j(\omega-n\Omega_{s})]
\end{align}
s(t)=n=−∞∑+∞δ(t−nTs)↔S(jω)fs(t)=f(t)⋅s(t)↔Fs(jω)=Ωsn=−∞∑+∞δ(ω−nΩs),Ωs=Ts2π=2π1F(jω)∗S(jω)=2π1F(jω)∗Ωsn=−∞∑+∞δ(ω−nΩs)=Ts1n=−∞∑+∞F[j(ω−nΩs)]
结论:
Fs(jω)=1Ts∑n=−∞+∞F[j(ω−nΩs)]
F_{s}(j\omega)=\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}F[j(\omega-n\Omega_{s})]
Fs(jω)=Ts1n=−∞∑+∞F[j(ω−nΩs)]
- Fs(jω)F_{s}(j\omega)Fs(jω)为信号频谱F(jω)F(j\omega)F(jω)以Ωs\Omega_{s}Ωs为周期延拓
- 频谱幅度变为原先的1T\frac{1}{T}T1
理想抽样信号及其频谱示意图:
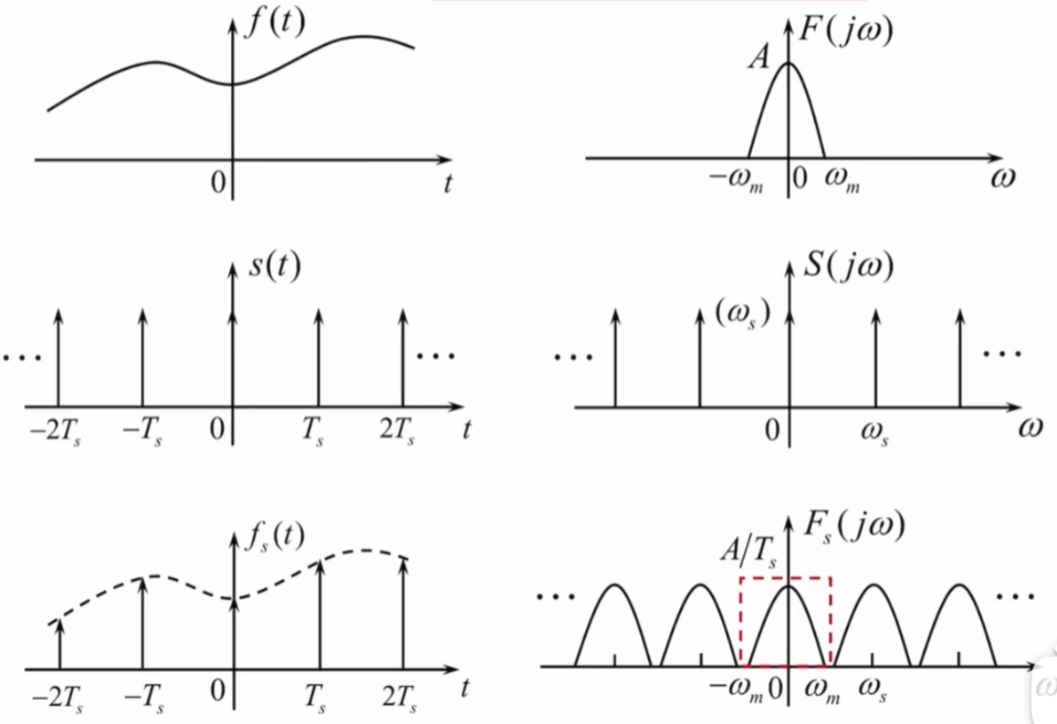
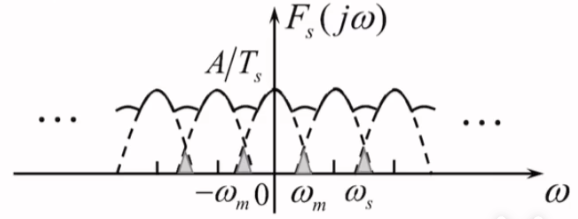
-
fs≥2fmf_{s}\geq 2f_{m}fs≥2fm时,各个频谱之间无混叠,可以分离出原信号的频谱
- 由抽样序列{f(nTs)}\{ f(nT_{s}) \}{f(nTs)}可以无失真地恢复出f(t)f(t)f(t)
-
fs<2fmf_{s}<2f_{m}fs<2fm时,频谱之间产生混叠,无法分离出原信号的频谱
- 由{f(nTs)}\{ f(nT_{s}) \}{f(nTs)}不能无失真地恢复f(t)f(t)f(t)
-
其中ωm\omega_{m}ωm为原式连续信号的最高角频率,代表频谱的有效带宽
例

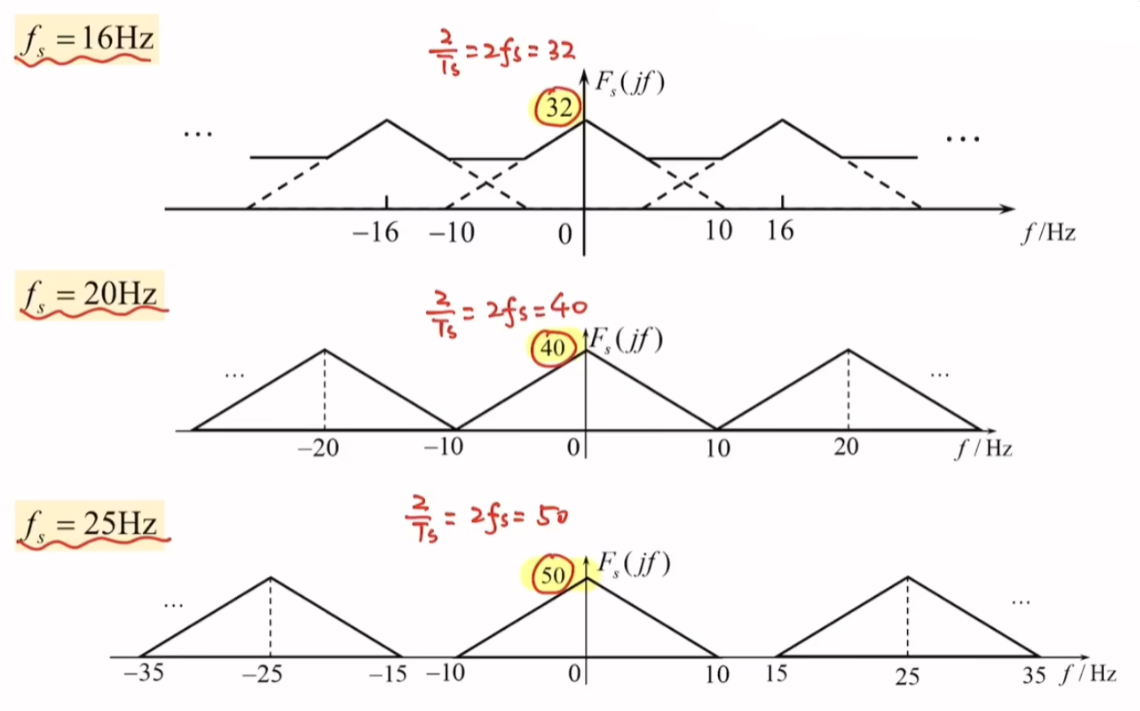
- 当fs<2fmf_{s}<2f_{m}fs<2fm时,频谱图像会存在重叠
矩形抽样及其信号的频谱
矩形抽样的定义:
抽样脉冲为矩形脉冲,此时抽样信号的脉冲顶部随着原信号f(t)f(t)f(t)变化,这样的抽样称为矩形抽样
矩形抽样的频谱:
设矩形脉冲脉宽为τ\tauτ,周期为TTT
s(t)=gτ(t)∗δT(t)S(jω)=τSa(ωτ2)⋅2πT∑n=−∞+∞δ(ω−nωs)=2πτTs∑n=−∞+∞Sa(nωsτ2)δ(ω−nωs)而fs(t)=f(t)⋅s(t)则Fs(jω)=12πF(jω)∗S(jω)=τT∑n=−∞+∞Sa(nωsτ2)F[j(ω−nωs)]
\begin{align}
s(t)&=g_{\tau}(t)*\delta_{T}(t)\\ \\
S(j\omega)&=\tau Sa\left( \frac{\omega \tau}{2} \right)\cdot \frac{2\pi}{T}\sum_{n=-\infty}^{+\infty}\delta(\omega-n\omega_{s})=\frac{2\pi \tau}{T_{s}}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)\delta(\omega-n\omega_{s})\\ \\
而f_{s}(t)&=f(t)\cdot s(t)\\ \\
则F_{s}(j\omega)&=\frac{1}{2\pi}F(j\omega)*S(j\omega)=\frac{\tau}{T}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)F[j(\omega-n\omega_{s})]
\end{align}
s(t)S(jω)而fs(t)则Fs(jω)=gτ(t)∗δT(t)=τSa(2ωτ)⋅T2πn=−∞∑+∞δ(ω−nωs)=Ts2πτn=−∞∑+∞Sa(2nωsτ)δ(ω−nωs)=f(t)⋅s(t)=2π1F(jω)∗S(jω)=Tτn=−∞∑+∞Sa(2nωsτ)F[j(ω−nωs)]
结论:
Fs(jω)=τTs∑n=−∞+∞Sa(nωsτ2)F[j(ω−nωs)]
F_{s}(j\omega)=\frac{\tau}{T_{s}}\sum_{n=-\infty}^{+\infty}Sa\left( \frac{n\omega_{s}\tau}{2} \right)F[j(\omega-n\omega_{s})]
Fs(jω)=Tsτn=−∞∑+∞Sa(2nωsτ)F[j(ω−nωs)]
- Fs(jω)F_{s}(j\omega)Fs(jω)为SaSaSa函数加权,包络满足SaSaSa函数的变化规律
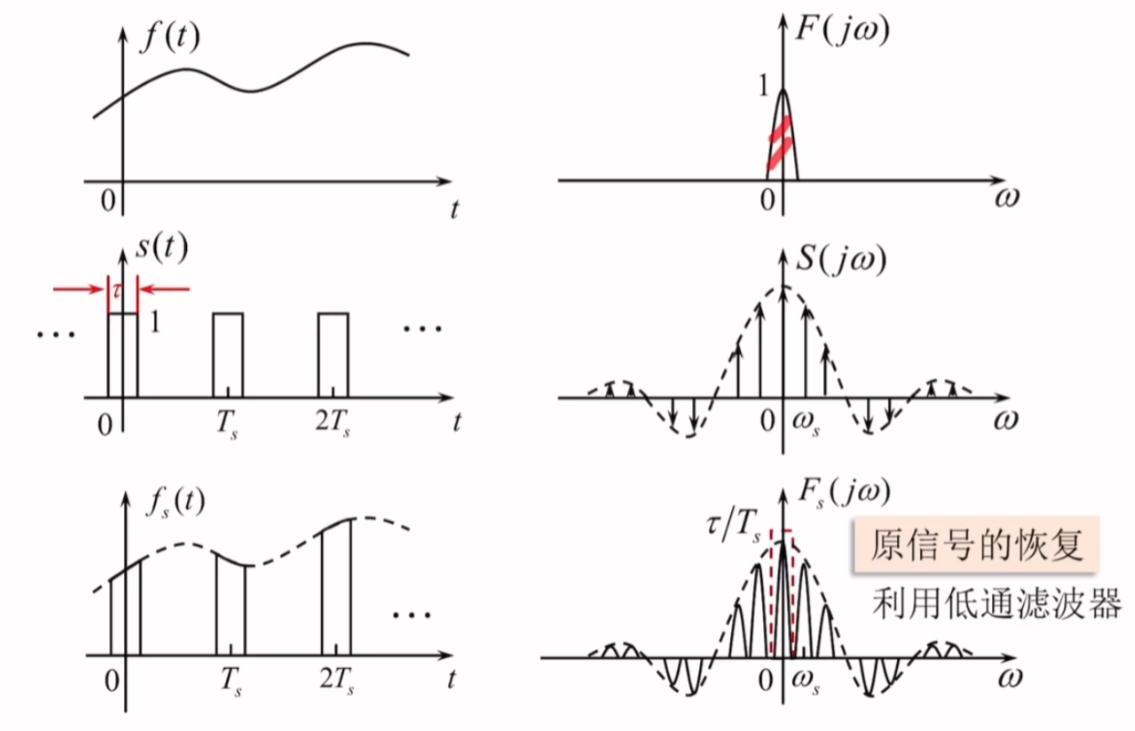
- 当fs≥2fmf_{s}\geq2 f_{m}fs≥2fm时,同样可以通过低通滤波器来还原出原信号
理想抽样与矩形抽样的异同点
相同点:
- 均为无穷多个间隔为ωs\omega_{s}ωs的F(jω)F(j\omega)F(jω)叠加而成的
- 抽样频率满足要求时,均可以通过低通滤波器恢复原信号
不同点:
- 矩形理想抽样信号频谱被常数加权,带宽无穷大
- 矩形抽样信号频谱被SaSaSa函数加权,最终收敛于0,第一过零点带宽为Bω=2πτ(rad/s)B_{\omega}=\frac{2\pi}{\tau}(rad/s)Bω=τ2π(rad/s)或Bf=1τ(Hz)B_{f}=\frac{1}{\tau}(Hz)Bf=τ1(Hz)
提高传输速度⇔矛盾压缩传输带宽 提高传输速度\xLeftrightarrow{矛盾}压缩传输带宽 提高传输速度矛盾压缩传输带宽
时域抽样定理
- fs≥2fmf_{s}\geq{2}f_{m}fs≥2fm时,各个频谱之间没有混叠,可以分离出原信号的频谱
- fs<2fmf_{s}<2f_{m}fs<2fm时,频谱之间产生混叠,无法分离出原信号的频谱
定理:
一个频带限制在(0,fm)(0,f_{m})(0,fm)内的低通信号f(t)f(t)f(t),如果以fs≥2fmf_{s}\geq2 f_{m}fs≥2fm的速率进行均匀抽样,则由抽样序列{f(nTs)}\{ f(nT_{s}) \}{f(nTs)}可以无失真恢复出f(t)f(t)f(t)
奈奎斯特抽样速率:fs=2fm ⟹ 最小抽样速率奈奎斯特抽样间隔:Ts=12fm ⟹ 最大抽样间隔
\begin{align}
&奈奎斯特抽样速率:f_{s}=2f_{m}\implies最小抽样速率\\ \\
&奈奎斯特抽样间隔:T_{s}=\frac{1}{2f_{m}}\implies最大抽样间隔
\end{align}
奈奎斯特抽样速率:fs=2fm⟹最小抽样速率奈奎斯特抽样间隔:Ts=2fm1⟹最大抽样间隔
在工程中,若信号不是频带有限信号,则往往通过截止频率fmf_{m}fm的低通滤波器让其频带有限,称为抗混叠滤波
例
若信号f1(t)f_{1}(t)f1(t)和f2(t)f_{2}(t)f2(t)的最高角频率分别为3π×105rad/s3\pi \times 10^{5}rad/s3π×105rad/s和2π×105rad/s2\pi \times 10^5rad/s2π×105rad/s,试求下列信号进行时域抽样时的奈奎斯特抽样频率
1)f1(12t)f_{1}\left( \frac{1}{2}t \right)f1(21t)
f1=ω1m2π=1.5×105Hz,f2=ω2m2π=105Hzf1(12t)↔2F1(j⋅2ω)→拉伸fm=12f1=7.5×104Hz ⟹ fs=2fm=1.5×105Hz
\begin{align}
&f_{1}=\frac{\omega_{1m}}{2\pi}=1.5\times 10^{5}Hz,f_{2}=\frac{\omega_{2m}}{2\pi}=10^{5}Hz\\ \\
&f_{1}\left( \frac{1}{2}t \right)\leftrightarrow 2F_{1}(j\cdot 2\omega)\xrightarrow{拉伸} f_{m}=\frac{1}{2}f_{1}=7.5\times 10^{4}Hz\\ \\
&\implies f_{s}=2f_{m}=1.5\times 10^{5}Hz
\end{align}
f1=2πω1m=1.5×105Hz,f2=2πω2m=105Hzf1(21t)↔2F1(j⋅2ω)拉伸fm=21f1=7.5×104Hz⟹fs=2fm=1.5×105Hz
- 角频率有两种单位rad,Hzrad,Hzrad,Hz,其中radradrad单位除以2π2\pi2π后可以转换成HzHzHz
2)f23(t)f_{2}^{3}(t)f23(t)
f23(t)↔1(2π)2[F2(jω)∗F2(jω)∗F2(jω)] ⟹ fm=3f2=3×105Hz ⟹ fs=2fm=6×105Hz
\begin{align}
&f_{2}^{3}(t)\leftrightarrow \frac{1}{(2\pi)^{2}}[F_{2}(j\omega)*F_{2}(j\omega)*F_{2}(j\omega)]\\ \\
&\implies f_{m}=3f_{2}=3\times 10^{5}Hz\\ \\
&\implies f_{s}=2f_{m}=6\times 10^{5}Hz
\end{align}
f23(t)↔(2π)21[F2(jω)∗F2(jω)∗F2(jω)]⟹fm=3f2=3×105Hz⟹fs=2fm=6×105Hz
- 利用卷积积分的定义域叠加性质:
- 若f(t)f(t)f(t)定义域为[t1,t2][t_{1},t_{2}][t1,t2],g(t)g(t)g(t)的定义域为[t3,t4][t_{3},t_{4}][t3,t4]
- 则f(t)∗g(t)f(t)*g(t)f(t)∗g(t)定义域为[t1+t3,t2+t4][t_{1}+t_{3},t_{2}+t_{4}][t1+t3,t2+t4]
- 三次自卷积后,最高角频率扩大三倍
3)f1(t)⋅f2(t)f_{1}(t)\cdot f_{2}(t)f1(t)⋅f2(t)
f1(t)⋅f2(t)↔12πF1(jω)∗F2(jω)fm=f1+f2=2.5×105Hz ⟹ fs=2fm=5×105Hz
\begin{align}
&f_{1}(t)\cdot f_{2}(t)\leftrightarrow \frac{1}{2\pi}F_{1}(j\omega)*F_{2}(j\omega)\\ \\
&f_{m}=f_{1}+f_{2}=2.5\times 10^{5}Hz\\ \\
&\implies f_{s}=2f_{m}=5\times 10^{5}Hz
\end{align}
f1(t)⋅f2(t)↔2π1F1(jω)∗F2(jω)fm=f1+f2=2.5×105Hz⟹fs=2fm=5×105Hz
4)f1(t)∗f2(2t)f_{1}(t)*f_{2}(2t)f1(t)∗f2(2t)
f1(t)∗f2(2t)↔F1(jω)⋅12F2(12jω)fm=min{f1,2f2}=f1=3×105Hz
\begin{align}
&f_{1}(t)*f_{2}(2t)\leftrightarrow F_{1}(j\omega)\cdot \frac{1}{2}F_{2}\left( \frac{1}{2}j\omega \right)\\ \\
&f_{m}=min\{ f_{1},2f_{2} \}=f_{1}=3\times 10^{5}Hz
\end{align}
f1(t)∗f2(2t)↔F1(jω)⋅21F2(21jω)fm=min{f1,2f2}=f1=3×105Hz
- 两个信号做乘法,新信号的最高角频率为两个原信号最高角频率中的最小值
5)f1(t)+f2(2t)f_{1}(t)+f_{2}(2t)f1(t)+f2(2t)
f1(t)+f2(2t)↔F1(jω)+12F2(12jω) ⟹ fm=max{f1,2f2}=2×105Hz
\begin{align}
&f_{1}(t)+f_{2}(2t)\leftrightarrow F_{1}(j\omega)+\frac{1}{2}F_{2}\left( \frac{1}{2}j\omega \right)\\ \\
&\implies f_{m}=max\{ f_{1},2f_{2} \}=2\times 10^{5}Hz
\end{align}
f1(t)+f2(2t)↔F1(jω)+21F2(21jω)⟹fm=max{f1,2f2}=2×105Hz
- 两个信号做加法,新信号的最高角频率为两个原信号的最高角频率中的最大值

- 注意F(j⋅ωα)F\left( j\cdot \frac{\omega}{\alpha} \right)F(j⋅αω)所对应的最高角频率为∣α∣ω|\alpha|\omega∣α∣ω
时域原信号的恢复
利用低通滤波器来恢复原信号
H(jω)={Ts,∣ω∣≤ωc0,∣ω∣>ωc=Ts⋅g2ωc(ω)
\begin{align}
H(j\omega)&=\begin{cases}
T_{s},\quad |\omega|\leq \omega_{c}\\ \\
0,\quad |\omega|>\omega_{c}
\end{cases}\\ \\
&=T_{s}\cdot g_{2\omega _{c}}(\omega)
\end{align}
H(jω)=⎩⎨⎧Ts,∣ω∣≤ωc0,∣ω∣>ωc=Ts⋅g2ωc(ω)
截止频率需要满足:
ωm≤ωc≤ωs−ωm
\omega_{m}\leq \omega_{c}\le \omega_{s}-\omega_{m}
ωm≤ωc≤ωs−ωm
- 恰好卡在最大角频率与下一个周期开始的位置之间
例
带限信号f(t)f(t)f(t)的最高频率为300Hz300Hz300Hz,若对y(t)=12[f(t3)∗f(2t)]⋅f(t)y(t)=\frac{1}{2}\left[ f\left( \frac{t}{3} \right)*f(2t) \right]\cdot f(t)y(t)=21[f(3t)∗f(2t)]⋅f(t)以Ts=1msT_{s}=1msTs=1ms进行抽样,低通滤波器的截止频率fcf_{c}fc应该满足什么范围?
若f(t)∼fm则f(t3)∼fm3 , f(2t)∼2fmf(t3)∗f(2t)↔F(t3)⋅F(2t)∼min{fm3,2fm}=fm3[f(t3)∗f(2t)]⋅f(t)↔12π[F(t3)⋅F(2t)]∗F(t)∼fm3+fm∴y(t)∼fm′=43fmfm′≤fc≤fs−fm′
\begin{align}
&若f(t)\sim f_{m}\\ \\
&则f\left( \frac{t}{3} \right)\sim \frac{f_{m}}{3}\ ,\ f(2t)\sim 2f_{m}\\ \\
&f\left( \frac{t}{3} \right)*f(2t)\leftrightarrow F\left( \frac{t}{3} \right)\cdot F(2t)\sim min\left\{ \frac{f_{m}}{3},2f_{m} \right\}=\frac{f_{m}}{3}\\ \\
&\left[ f\left( \frac{t}{3} \right)*f(2t) \right]\cdot f(t)\leftrightarrow \frac{1}{2\pi}\left[ F\left( \frac{t}{3} \right)\cdot F(2t) \right]*F(t)\sim \frac{f_{m}}{3}+f_{m}\\ \\
&\therefore y(t)\sim f_{m}'=\frac{4}{3}f_{m}\\ \\
&f'_{m}\leq f_{c}\leq f_{s}-f_{m}'
\end{align}
若f(t)∼fm则f(3t)∼3fm , f(2t)∼2fmf(3t)∗f(2t)↔F(3t)⋅F(2t)∼min{3fm,2fm}=3fm[f(3t)∗f(2t)]⋅f(t)↔2π1[F(3t)⋅F(2t)]∗F(t)∼3fm+fm∴y(t)∼fm′=34fmfm′≤fc≤fs−fm′
内插公式
假设fs=2fm,ωc=ωmf_{s}=2f_{m},\omega_{c}=\omega_{m}fs=2fm,ωc=ωm:
F(jω)=F(jω)⋅H(jω)↔f(t)=fs(t)∗h(t)H(jω)={Ts∣ω∣≤ωm0∣ω∣>ωm=Tsg2ωm(ω)↔h(t)=Tssinωmtπt=Sa(ωmt) ⟹ f(t)=fs(t)∗h(t)=∑n=−∞+∞f(nTs)δ(t−nTs)∗Sa(ωmt)=∑n=−∞+∞f(nTs)Sa[ωm(t−nTs)]
\begin{align}
&F(j\omega)=F(j\omega)\cdot H(j\omega)\leftrightarrow f(t)=f_{s}(t)*h(t)\\ \\
&H(j\omega)=\begin{cases}
T_{s}\quad |\omega|\leq \omega_{m}\\ \\
0\quad | \omega|>\omega_{m}
\end{cases}=T_{s}g_{2\omega_{m}}(\omega)\leftrightarrow h(t)=T_{s} \frac{\sin \omega_{m}t}{\pi t}=Sa(\omega_{m}t)\\ \\
\implies f(t)&=f_{s}(t)*h(t)=\sum_{n=-\infty}^{+\infty}f(nT_{s})\delta(t-nT_{s})*Sa(\omega_{m}t)\\ \\
&=\sum_{n=-\infty}^{+\infty}f(nT_{s})Sa[\omega_{m}(t-nT_{s})]
\end{align}
⟹f(t)F(jω)=F(jω)⋅H(jω)↔f(t)=fs(t)∗h(t)H(jω)=⎩⎨⎧Ts∣ω∣≤ωm0∣ω∣>ωm=Tsg2ωm(ω)↔h(t)=Tsπtsinωmt=Sa(ωmt)=fs(t)∗h(t)=n=−∞∑+∞f(nTs)δ(t−nTs)∗Sa(ωmt)=n=−∞∑+∞f(nTs)Sa[ωm(t−nTs)]
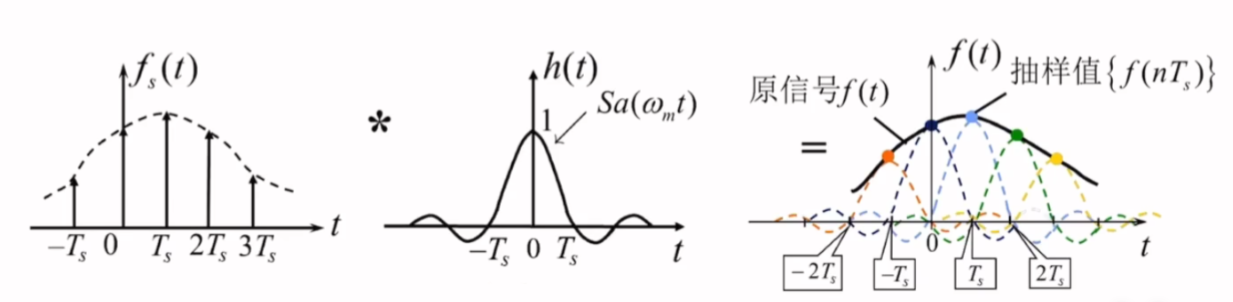
- 其中,Sa[ωm(t−nTs)]Sa[\omega_{m}(t-nT_{s})]Sa[ωm(t−nTs)]称为内插函数
- 在恢复原信号的时候,抽样时刻t=nTst=nT_st=nTs的值由抽样值f(nTs)f(nT_{s})f(nTs)确定,抽样时刻之外的信号值是无穷项内插函数的加权和
- 内插函数在取kTskT_{s}kTs时,只有nTsnT_{s}nTs时为1,其余时刻为0,因此不同的内插函数求和时不会影响kTskT_{s}kTs的值