量子计算学习笔记(2)
这里写目录标题
- 量子计算核心原理学习笔记(2)
- 量子计算的基本定义回顾
- 狄拉克符号、内积与外积
- 可逆计算
- 量子计算的核心假设
量子计算核心原理学习笔记(2)
量子计算的基本定义回顾
经典比特与量子比特的区别。
经典比特是一个确定的0或1,物理上可通过三极管的高低电平实现。
而量子计算的基本单位是量子比特 (Qubit),它是一个量子态,可以表示为两个基本计算基矢 ∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 的线性叠加。
其数学形式为一个二维复数向量:∣ψ⟩=a∣0⟩+b∣1⟩|\psi\rangle = a|0\rangle + b|1\rangle∣ψ⟩=a∣0⟩+b∣1⟩,其中 aaa 和 bbb 是复数概率幅,必须满足归一化条件 ∣a∣2+∣b∣2=1|a|^2 + |b|^2 = 1∣a∣2+∣b∣2=1。在向量表示法中,基矢定义为 ∣0⟩≡(10)|0\rangle \equiv \begin{pmatrix} 1 \\ 0 \end{pmatrix}∣0⟩≡(10) 和 ∣1⟩≡(01)|1\rangle \equiv \begin{pmatrix} 0 \\ 1 \end{pmatrix}∣1⟩≡(01),因此任意量子态可写作 ∣ψ⟩=(ab)|\psi\rangle = \begin{pmatrix} a \\ b \end{pmatrix}∣ψ⟩=(ab)。
∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 为一组计算基 (computational basis)。
狄拉克符号、内积与外积
量子力学中广泛使用狄拉克符号。其中,∣ψ⟩|\psi\rangle∣ψ⟩ (ket)代表一个列向量。
与之对应,其共轭转置(一个行向量)被称为bra,记作⟨ψ∣\langle\psi|⟨ψ∣。
若∣ψ⟩=(ab)|\psi\rangle = \begin{pmatrix} a \\ b \end{pmatrix}∣ψ⟩=(ab),则⟨ψ∣=(a∗,b∗)\langle\psi| = (a^*, b^*)⟨ψ∣=(a∗,b∗)。这个命名源于将括号(bracket)拆分为bra和ket两部分。

内积 (Inner Product):由一个bra和一个ket构成,如⟨ϕ∣ψ⟩\langle\phi|\psi\rangle⟨ϕ∣ψ⟩,结果是一个标量(复数)。
外积 (Outer Product):由一个ket和一个bra构成,如∣ψ⟩⟨ϕ∣|\psi\rangle\langle\phi|∣ψ⟩⟨ϕ∣,结果是一个矩阵或算符。例如,∣0⟩⟨0∣+∣1⟩⟨1∣=(10)(1,0)+(01)(0,1)=(1000)+(0001)=(1001)=I|0\rangle\langle0| + |1\rangle\langle1| = \begin{pmatrix} 1 \\ 0 \end{pmatrix}(1, 0) + \begin{pmatrix} 0 \\ 1 \end{pmatrix}(0, 1) = \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} + \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = I∣0⟩⟨0∣+∣1⟩⟨1∣=(10)(1,0)+(01)(0,1)=(1000)+(0001)=(1001)=I,这是单位矩阵。
可逆计算
要理解如何对量子比特进行操作,可以先从经典计算中的逻辑门出发。
诸如与门 (AND)、或门 (OR) 和非门 (NOT) 构成了经典计算的基础。一个重要的概念是通用门集合 (Universal Gate Set),即能够通过组合实现任意布尔函数的一组门。例如,{与门, 或门, 非门} 就是一个通用集合,而与非门 (NAND) 本身也是通用的。
经典计算的一个关键特点是其操作通常不可逆。
例如,一个与门的输出为0,我们无法反推出其输入是(0,0), (0,1)还是(1,0),这个过程丢失了信息。然而,量子力学中的演化是可逆的,因此量子计算也必须是可逆计算 (Reversible Computation)。
为了解决这个问题,可以通过引入额外的比特,即 Ancilla 比特,来将任意不可逆的经典计算转化为可逆计算。
一个典型的可逆通用门是Toffoli门。它有三个输入和三个输出 (x,y,z)(x, y, z)(x,y,z),其操作定义为将输入映射到 (x,y,z⊕(x∧y))(x, y, z \oplus (x \land y))(x,y,z⊕(x∧y))。通过巧妙设置输入,例如将 zzz 设为0,第三个输出就变成了 x∧yx \land yx∧y,从而实现了与门的功能。由于Toffoli门是可逆且通用的,这证明了任何经典计算都可以被一个可逆的计算过程所模拟。
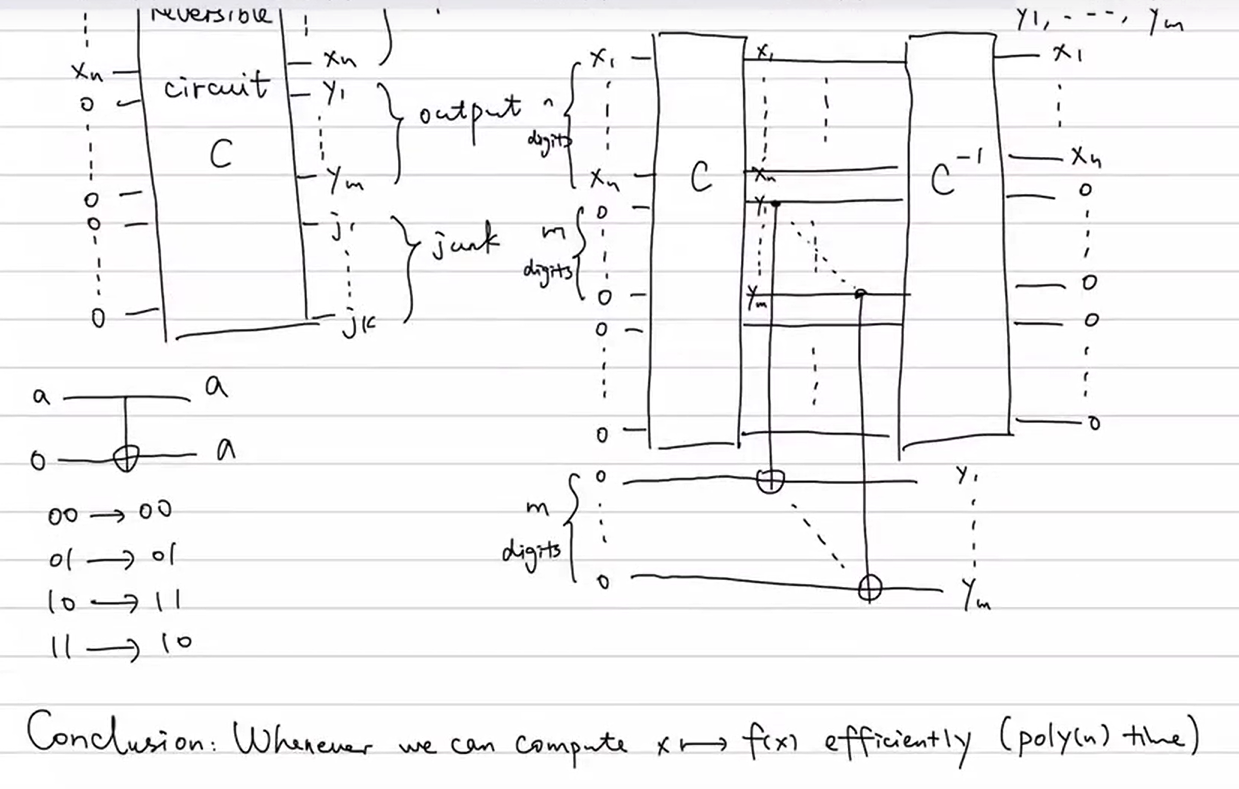
在可逆计算中,Ancilla比特在完成计算后会变成不再需要的“垃圾”信息。清理这些垃圾比特的标准方法是先将计算结果复制出来,然后逆向运行同样的计算电路,这会将Ancilla比特恢复到初始的零状态。
量子计算的核心假设
量子计算遵循量子力学的基本假设,这些假设构成了其数学和物理框架。
-
假设一:量子态 (State Space)
一个孤立量子系统的状态由一个复数向量空间中的单位向量(也称态向量)完全描述。
对于单个量子比特,这是一个二维复向量空间。
该状态可以通过布洛赫球面 (Bloch Sphere) 进行几何可视化。球面上任意一点都对应一个纯态,其参数化形式为:
∣ψ⟩=cos(θ2)∣0⟩+eiϕsin(θ2)∣1⟩|\psi\rangle = \cos(\frac{\theta}{2})|0\rangle + e^{i\phi}\sin(\frac{\theta}{2})|1\rangle∣ψ⟩=cos(2θ)∣0⟩+eiϕsin(2θ)∣1⟩
其中,全体相位因子 eiαe^{i\alpha}eiα 不影响物理实在,因此可以忽略。∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 分别对应球面的北极和南极。XXX轴的正方向对应∣+⟩=12(∣0⟩+∣1⟩)|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)∣+⟩=21(∣0⟩+∣1⟩),YYY轴的正方向对应12(∣0⟩+i∣1⟩)\frac{1}{\sqrt{2}}(|0\rangle + i|1\rangle)21(∣0⟩+i∣1⟩)。
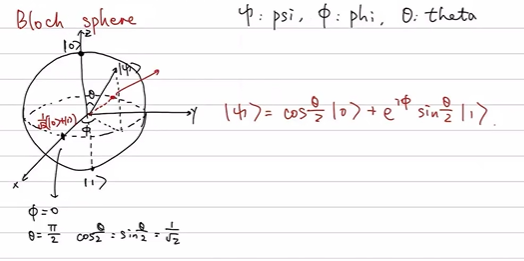
-
假设二:量子演化 (Quantum Dynamics)
一个封闭量子系统的演化过程是线性的,并且可以用一个幺正变换 (Unitary Transformation) 来描述。
如果系统在 t1t_1t1 时刻的状态是 ∣ψ1⟩|\psi_1\rangle∣ψ1⟩,在 t2t_2t2 时刻的状态是 ∣ψ2⟩|\psi_2\rangle∣ψ2⟩,那么必然存在一个幺正矩阵 UUU 使得 ∣ψ2⟩=U∣ψ1⟩|\psi_2\rangle = U|\psi_1\rangle∣ψ2⟩=U∣ψ1⟩。幺正矩阵的定义是 U†U=UU†=IU^\dagger U = UU^\dagger = IU†U=UU†=I,其中 U†U^\daggerU† 是 UUU 的共轭转置。
这种幺正演化保证了系统的总概率(即向量的范数)守恒。这个规则来源于物理学中的薛定谔方程。

常见的单比特量子门,如Pauli门、Hadamard门(H)、Phase门(S)和T门,都是幺正矩阵的例子。

-
假设三:复合系统 (Composite Systems)
当多个量子系统组合成一个复合系统时,其状态空间是各个子系统状态空间的张量积 (Tensor Product)。
例如,一个由两个量子比特组成的系统,其状态空间是两个二维空间的张量积,形成一个四维空间。
如果第一个量子比特的状态是 ∣ψ⟩=a∣0⟩+b∣1⟩|\psi\rangle = a|0\rangle + b|1\rangle∣ψ⟩=a∣0⟩+b∣1⟩,第二个是 ∣ϕ⟩=c∣0⟩+d∣1⟩|\phi\rangle = c|0\rangle + d|1\rangle∣ϕ⟩=c∣0⟩+d∣1⟩,那么复合系统的状态就是:∣ψ⟩⊗∣ϕ⟩=(a∣0⟩+b∣1⟩)⊗(c∣0⟩+d∣1⟩)=ac∣00⟩+ad∣01⟩+bc∣10⟩+bd∣11⟩|\psi\rangle \otimes |\phi\rangle = (a|0\rangle + b|1\rangle) \otimes (c|0\rangle + d|1\rangle) = ac|00\rangle + ad|01\rangle + bc|10\rangle + bd|11\rangle∣ψ⟩⊗∣ϕ⟩=(a∣0⟩+b∣1⟩)⊗(c∣0⟩+d∣1⟩)=ac∣00⟩+ad∣01⟩+bc∣10⟩+bd∣11⟩。

这种可以写成两个子系统张量积形式的状态被称为乘积态 (Product State)。
然而,并非所有复合系统的状态都是乘积态。那些不能被分解为子系统张量积的状态,被称为纠缠态 (Entangled State),例如著名的贝尔态 12(∣00⟩+∣11⟩)\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)21(∣00⟩+∣11⟩) 就是一个纠缠态。

