CF Yamakasi (前缀和+双指针）

https://codeforces.com/contest/2121/problem/F

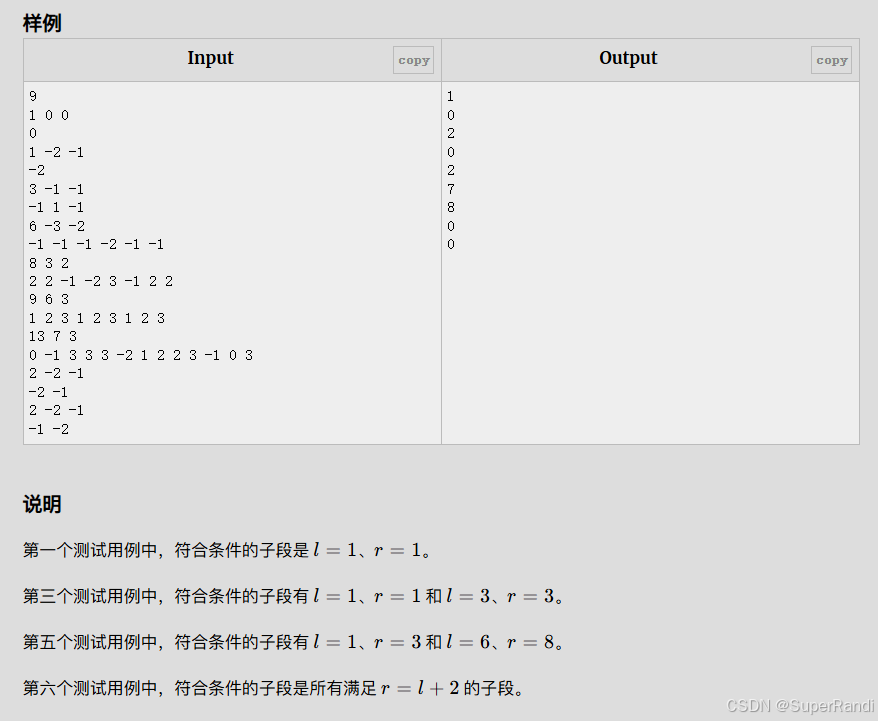
思路：这道题是在求子段和为s的个数问题上增加了子段的最大值得为x的条件

           如果单纯地要我们计算子段和为s的个数那怎么求呢，首先子段和快速求解得用到前缀和，所以我们可以得到式子pre[r]-pre[l]=s，即区间[l+1,r]满足和为s,我们可以通过计算l<r中满足pre[l]=pre[r]-s的左端点个数，从而得到以r为右端点的子段和为s的个数，这样我们只需要O(n)的时间就可以得到整个数组满足子段和为s的个数。

          但题目增加了子段中的最大值必须为x的限制，因为pre[r]-pre[l]=s，所以在[l+1,r]的区间中必须含有x，而l一定在x的左边，只有当碰到新的x时l才能向右移动计数，或者碰到比x大的数l直接等于这个更大的数的位置，直到碰到x才进行更新。同时我们要对该区间x是否为最大值进行标记，只有当区间最大值为x时才能对答案进行加pre[r]-s个数的操作。

Code:

void solve()
{int n,s,x;cin>>n>>s>>x;vector<int> v(n+1),pre(n+1,0);for(int i=1;i<=n;i++){cin>>v[i];pre[i]=pre[i-1]+v[i];}map<int,int> mp;int cnt=0;bool st=false;int l=0;for(int i=1;i<=n;i++){if(v[i]==x){st=true;while(l<i) mp[pre[l++]]++;}if(v[i]>x){st=false;l=i;mp.clear();}if(st) cnt+=mp[pre[i]-s];}cout<<cnt<<endl;
}