得物笔试题

选择题

什么是装饰器模式？

装饰器模式（Decorator Pattern）是面向对象设计模式中的一种结构型模式。它的核心思想是：在不修改原有对象代码的前提下，动态地给对象添加新的功能或职责。

继承（Inheritance）：
是静态的，在编译时就确定了。
如果功能组合很多（如咖啡+牛奶、咖啡+糖、咖啡+牛奶+糖、咖啡+巧克力…），你需要创建大量的子类，导致类爆炸。
不灵活，难以在运行时改变行为。
装饰器模式（Composition）：
是动态的，在运行时通过组合来添加功能。
功能可以自由组合，避免了类爆炸。
更加灵活和可扩展。

如何理解文法二义性？

理解文法的二义性（Ambiguity in Grammar）是编译原理和形式语言理论中的一个核心概念。简单来说，如果一个文法可以为同一个句子生成多棵不同的语法树（或最左/最右推导），那么这个文法就是二义性的。

最小生成树算法？

最小生成树（Minimum Spanning Tree, MST）是图论中的一个经典问题。给定一个连通、无向、带权图，最小生成树是原图的一个子图，它满足：

是一棵树：无环且连通。
包含所有顶点：覆盖图中的每一个顶点。
总权重最小：所有边的权重之和是所有可能生成树中最小的。
最小生成树在实际中有广泛应用，如：

设计成本最低的网络（公路、电网、通信网）。
聚类分析。
近似算法的基础（如旅行商问题）。
解决最小生成树问题主要有两种经典算法：Kruskal 算法 和 Prim 算法。

Kruskal 算法

**核心思想：**贪心 + 并查集。按边的权重从小到大排序，依次选择边，如果这条边连接的两个顶点不在同一个连通分量中（即不会形成环），就将其加入 MST。
算法步骤：
将图中的所有边按权重升序排序。
初始化一个空的 MST 集合。
初始化一个并查集 (Union-Find) 数据结构，用于管理顶点的连通性。
遍历排序后的每一条边 (u, v, weight)：
使用并查集检查 u 和 v 是否属于同一个连通分量。
如果不属于（即不会形成环），则将这条边加入 MST，并在并查集中将 u 和 v 合并。
如果属于，则跳过这条边（避免成环）。
当 MST 中的边数达到 V-1（V 是顶点数）时，算法结束。
时间复杂度：(O(E \log E))，主要消耗在边的排序上（E 是边数）。
**适用场景：**稀疏图（边数远小于顶点数的平方）表现良好。

Prim 算

核心思想： 贪心 + 优先队列。从一个起始顶点开始，维护一个MST 集合。每次选择一条连接 MST 集合与非 MST 集合的权重最小的边（称为“横切边”），将其加入 MST，直到所有顶点都被包含。
算法步骤：
选择一个起始顶点（通常选 0），将其加入 MST 集合。
使用一个优先队列（最小堆） 来存储所有从 MST 集合指向非 MST 集合的边，按权重排序。
当 MST 集合未包含所有顶点时：
从优先队列中取出权重最小的边 (u, v, weight)，其中 u 在 MST 中，v 不在。
将顶点 v 和这条边加入 MST。
将 v 的所有邻接边（指向非 MST 顶点的）加入优先队列。
重复直到 MST 包含所有顶点。
时间复杂度：
使用邻接矩阵 + 数组：(O(V^2))。
使用邻接表 + 优先队列（堆）：(O((V + E) \log V))。
**适用场景：**稠密图（边数接近 (V^{2)）时，(O(V}2)) 的 Prim 算法可能比 Kruskal 更优。

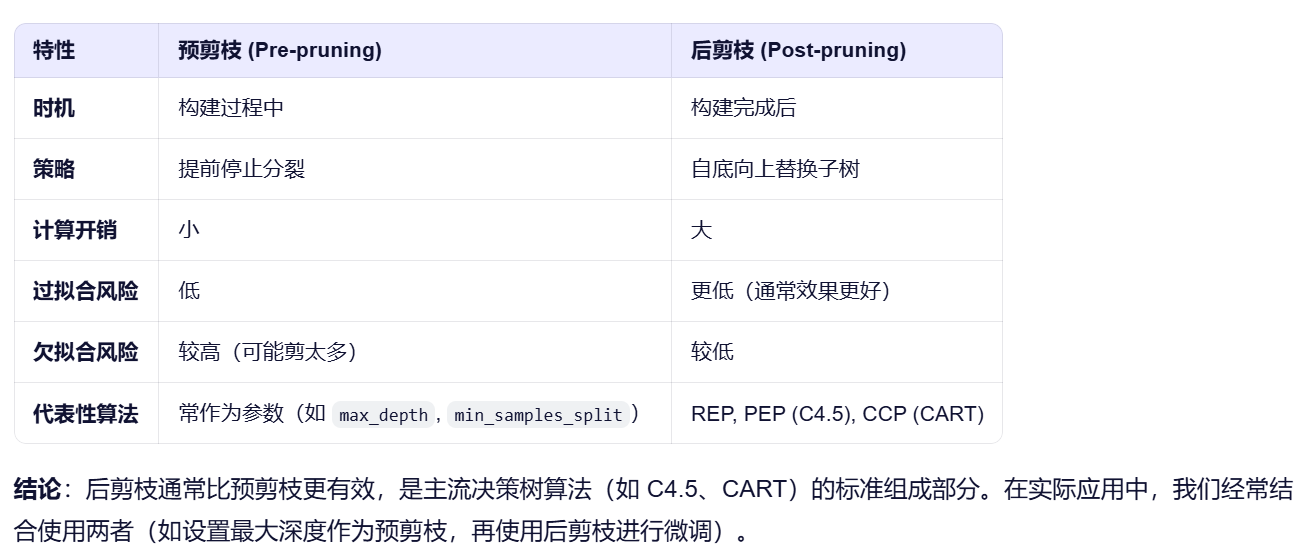
决策树剪枝？

决策树剪枝（Decision Tree Pruning）是机器学习中用于防止决策树过拟合（Overfitting） 的关键技术。它通过主动移除决策树中一些对分类贡献不大或仅针对训练数据噪声的分支，来简化树的结构，从而提高模型在未知数据（测试集）上的泛化能力。

过拟合问题：
决策树算法（如 ID3、C4.5、CART）通常会递归地分裂节点，直到每个叶节点都尽可能“纯净”（即包含同一类别的样本）。
这会导致生成一棵非常深、非常复杂的树，完美拟合了训练数据，包括其中的噪声和异常值。
这样的树在训练集上表现很好，但在新数据上表现很差，即泛化能力差。
模型复杂度与泛化能力的权衡：
剪枝通过降低模型复杂度，牺牲一部分训练集精度，来换取更好的测试集性能。

Q-Learning

Q-Learning 是一种无模型（Model-Free） 的 强化学习（Reinforcement Learning, RL） 算法，用于解决马尔可夫决策过程（Markov Decision Process, MDP） 问题。它的核心目标是让智能体（Agent）通过与环境的交互，学习一个最优策略，从而最大化长期累积奖励。

如何理解蒙特卡洛，时间差？

“蒙特卡洛”（Monte Carlo, MC）和“时间差分”（Temporal Difference, TD）是强化学习中两种核心的学习方法，用于估计价值函数（如状态价值 V(s)或动作价值 Q(s,a)）。它们都基于贝尔曼方程的思想，但在如何获取目标值（Target）来更新当前估计方面有本质区别。

算法

对于 n 个选手，每个选手都有攻击值和防御值，例如 i 选手的攻击值和防御值分别为a_i和b_i, j选手的攻击值和防御值分别为 a_j和b_j,当且仅当a_i * b_j > a_j * b_i 时，认为i选手能够赢j选手，求每个人选手能赢的人？

给定一个数组以及一个值x,你可以对数组做以下两种操作：将数组中的某个值加一，将数组中的某个数字清除，问最少经过多少个操作可以使得数组的和刚好为x的倍数？

问题分析
给定：

一个数组 arr。
一个整数 x。
两种操作：
加一：将数组中某个元素 +1，代价为 1。
清除：将数组中某个元素移除，代价为 1。
目标：使剩余数组元素的和是 x 的倍数（即 sum % x == 0），并求最小操作次数。

关键观察
“清除”操作：移除一个元素 arr[i]，相当于从总和中减去 arr[i]，但代价是 1（操作次数）。
“加一”操作：对一个元素 +1，总和增加 1，代价是 1。我们可以对同一个元素多次加一。
模运算：我们只关心最终和对 x 取模的结果。目标是让 sum ≡ 0 (mod x)。
状态定义：我们可以用 dp[r] 表示当前数组和模 x 等于 r 时，所需的最小操作次数。