【数据结构】二叉树-图解深度优先搜索(递归法、迭代法)
二叉树的遍历方式
二叉树的遍历策略可以分为两种:深度优先(DFS)与 广度优先(BFS),递归法与迭代法则作为这类策略的实现方式。它们之间的关系可以形容为:遍历策略是“目标”,而实现方式是“手段”,且一种遍历策略可以用不同的实现方式来完成。
这里就先来讲解一下深度优先遍历。
深度优先遍历
深度优先搜索既可以使用递归法实现(基于 栈 结构实现),也可以使用迭代法实现(同样也基于 栈 结构实现)。前序遍历、中序遍历、后序遍历都属于深度优先遍历。
前序遍历(中 左 右)
二叉树的前序遍历,就是先输出根节点,再遍历左子树,最后遍历右子树(也就是中左右),遍历左子树和右子树的时候,同样遵循前序遍历的规则。
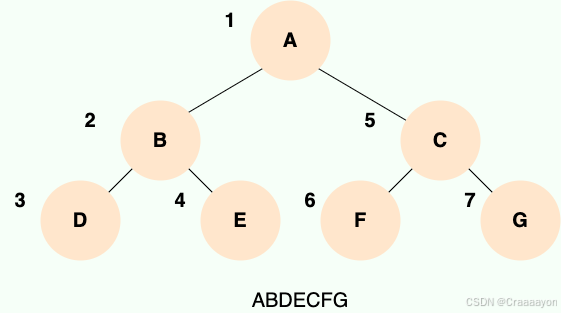
递归法思路如下:
public void preOrder(TreeNode root){if(root == null){return;}system.out.println(root.data);preOrder(root.left);preOrder(root.right);
}
迭代法思路如下:
- 根节点入栈
- 循环(栈不为空):
- 栈顶元素出栈并访问
- 右子节点入栈(如果存在)
- 左子节点入栈(如果存在)
为什么总是先右后左?因为栈是后进先出的,先压入右节点,再压入左节点,在出栈时就会先弹出左节点,再弹出右节点,这样就保证了"根→左→右"的访问顺序。
流程图及代码如下:

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>(); // 数组存储遍历结果if (root == null) return result;Deque<TreeNode> stack = new ArrayDeque<>(); // 双端队列作为栈stack.push(root); // 根节点入栈while (!stack.isEmpty()) {TreeNode node = stack.pop(); // 弹出栈顶元素result.add(node.val); // 访问当前节点// 先右后左,保证出栈时先左后右if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return result;
}
中序遍历(左 中 右)
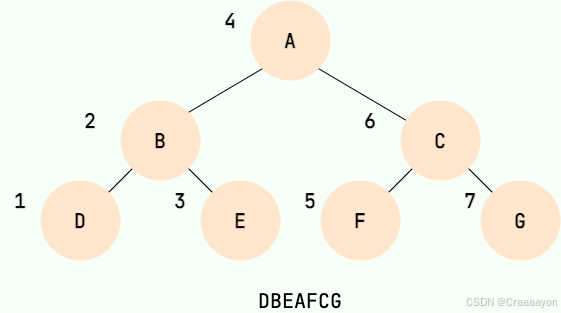
二叉树的中序遍历,就是先递归中序遍历左子树,再输出根结点的值,再递归中序遍历右子树(也就是左中右),大家可以想象成一巴掌把树压扁,父结点被拍到了左子节点和右子节点的中间,如下图所示:

递归法思路如下:
public void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);system.out.println(root.data);inOrder(root.right);
}
迭代法思路如下:
中序遍历的逻辑比较特别,因为在这里我们访问节点的顺序与处理的顺序不一样了,所以需要另外借助一个指针来帮助我们遍历二叉树。
- 进入循环,从根节点开始,将所有左子节点入栈
- 循环内(栈不为空 或 当前节点不为空):
- 将当前节点的所有左子节点入栈
- 弹出栈顶节点并访问
- 转向右子节点
流程图及代码如下:

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();Deque<TreeNode> stack = new ArrayDeque<>();TreeNode current = root; // 当前节点指针while (!stack.isEmpty() || current != null) {// 将当前节点的所有左子节点入栈while (current != null) {stack.push(current);current = current.left;}// 弹出栈顶节点(最左节点)current = stack.pop();result.add(current.val); // 访问该节点// 转向右子树current = current.right;}return result;
}
后序遍历(左 右 中)
二叉树的后序遍历,就是先递归后序遍历左子树,再递归后序遍历右子树(也就是左右中),最后输出根节点的值。
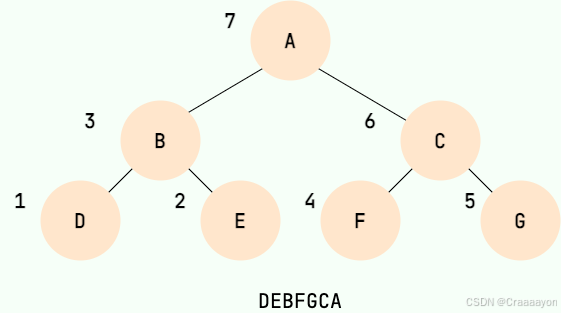
递归法思路如下:
public void postOrder(TreeNode root){if(root == null){return;}postOrder(root.left);postOrder(root.right);system.out.println(root.data);
}
迭代法思路如下:
- 根节点入栈
- 循环(栈不为空):
- 栈顶元素出栈并访问
- 左子节点入栈(如果存在)
- 右子节点入栈(如果存在)
- 翻转集合/数组
后续遍历的实现思路与前序遍历非常相似,简单来说我们就是需要将"中左右"的顺序转换为"左右中",可以分为以下两步来实现:1.将节点的入栈顺序改为先左后右,即"中右左";2.再反转集合/数组,即"左右中"。
流程图及代码如下:
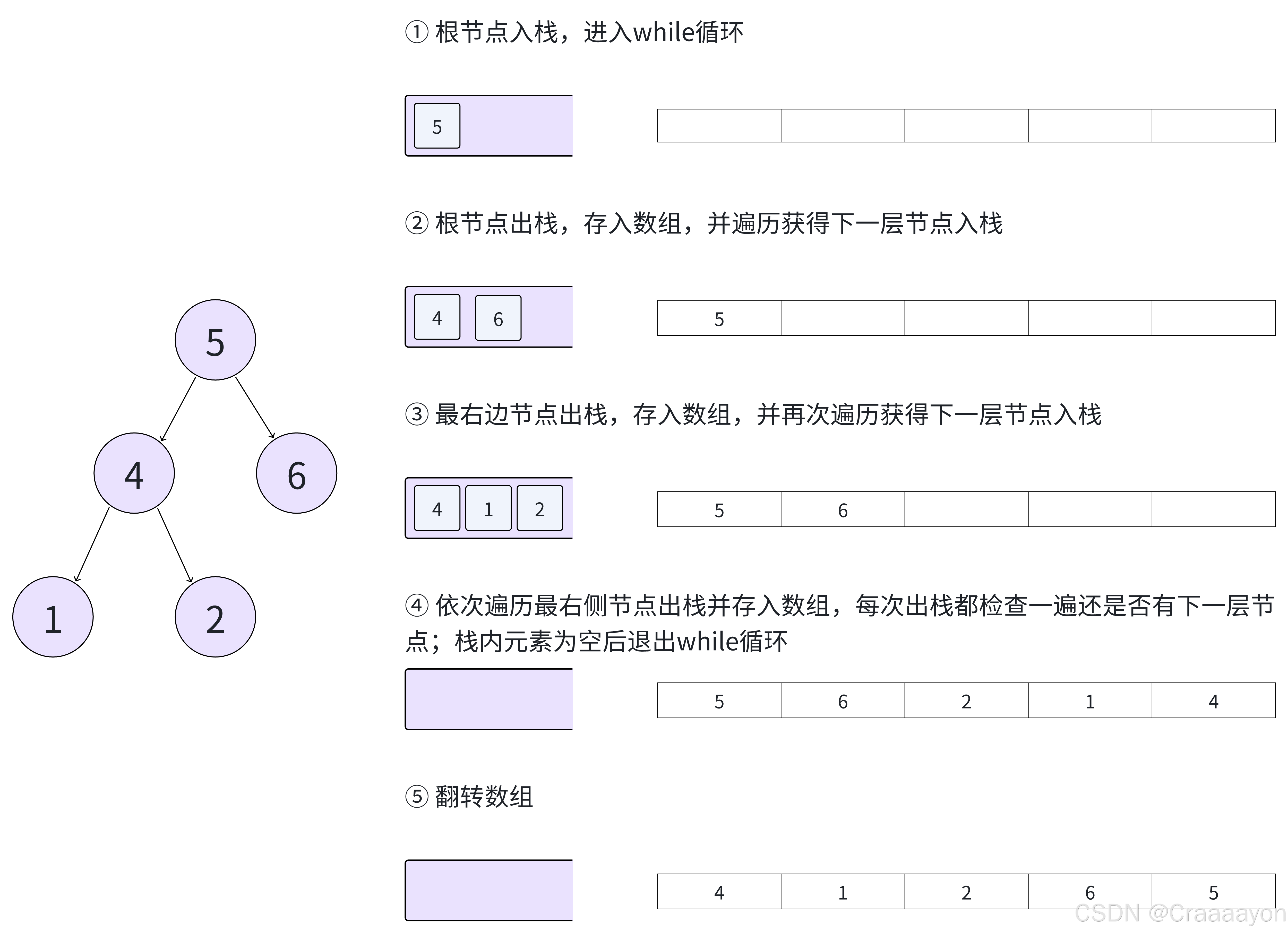
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>(); // 数组存储遍历结果if (root == null) return result;Deque<TreeNode> stack = new ArrayDeque<>(); // 双端队列作为栈stack.push(root); // 根节点入栈while (!stack.isEmpty()) {TreeNode node = stack.pop(); // 弹出栈顶元素result.add(node.val); // 访问当前节点// 先右后左,保证出栈时先左后右if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}// 反转结果:从左 -> 右 -> 根 变成 左 -> 右 -> 根Collections.reverse(result);return result;
}
