DeepSDF论文复现2---深入解析与代码复现2---原理分析与代码实现
DeepSDF论文复现2—深入解析与代码复现2—原理分析与代码实现
上一篇文章DeepSDF论文复现2—原理解析与代码复现1—官方代码运行 我们介绍了如何将DeepSDF的官方代码跑起来并进行可视化,不过没有涉及具体的实现原理,本篇我们将结合论文和官方代码来解析其实现原理。
原理解析
关于如何描述一个空间中的三维体,常用的为显式方法,有如下几种:
基于点云:三维体表面或者内部的点的集合
基于网格:将三个点连接为三角形,这样一个三角形表示三维体的一个表面对象,我们玩3D游戏看到的各种物体基本都是通过在网格上贴图然后添加光照的方式实现的
基于体素:类似于2D图像中的像素,把3D空间分割成类似256*256*256这样的一个个小方块,然后用方块是否存在标识三维体。《我的世界》这个游戏用的就是这个数据结构
这些方法存在的问题主要在于精度、处理速度和存储容量难以兼顾。比如,究竟要用多少个点才能比较好的表征三维体?用多了要存储和处理的数据就巨多,用少了又丢失很多细节。网格也是类似的,可以直接感受下下面两个游戏画面:

而体素比图像多了一个维度,数据量更是爆表,速度和精度难以兼得。
为了解决这些问题,最近这些年发展了很多通过神经网络来描述三维体的隐式表达方法。DeepSDF就是其中一个,它的源头是SDF(连续有符号距离函数),意思是使用公式来表述空间中的一个点到三维体表面的距离,如果这个点在三维体内部则为负值,否则为正值。另外,越靠近三维体表面值就越接近于0,如下面这张图描述的那样:
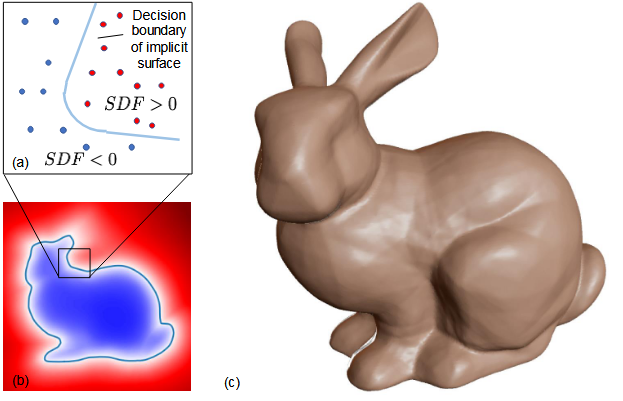
这个方法在早期没有发展的很好,原因在于要用公式描述一个空间点距离三维体表面的距离这件事实在太难了,想想都可怕。不要说三维体,就是描述二维平面一个点到物体表面的距离也不太好整。好就好在神经网络这些年发展起来了,它是一个能力超级强的公式拟合器,可以模拟任何巨变态的公式。因此DeepSDF论文的作者就提出了使用全连接神经网络来干这个活,结构如下面的图3(a):
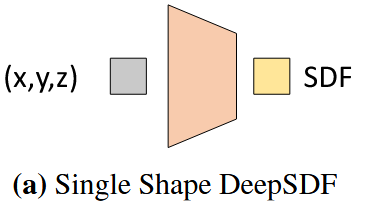
和之前手搓公式的逻辑是一模一样的,只是中间这个公式直接变成全连接神经网络。训练的方式也很简单,在数据集构建的时候就先计算出一堆空间点与三维体表面的距离,然后输入空间点,得到一个SDF值与SDF真值对比得到loss进行训练即可。
然而如果光这样子干的话,文章可能写四页就写完了,审稿人也会破口大骂。因此作者又进一步提出可以通过添加潜在向量的方式给同一类三维体进行编码,然后直接让网络学习整个类的物体的特征以及类中个体的具体表达,操作如图3(b):
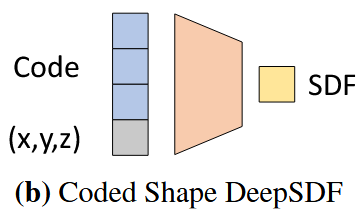
与前图的不同在于前图训练的是一个模型,而这个图训练的是一类模型。具体的,给一类模型中的每一个个体进行编号(文章称之为潜在向量,简单点说,假设一类模型,比如飞机,其中有2000个飞机的具体模型,我们就将其编号成1-2000),然后将个体编号与xyz一起扔进去网络进行训练。由于一类物体通常会有一些共同点,因此这个网络在理想的情况下既可以学到此类物体的一些共性又可以学到某个个体的特性。论文到此可以说平平无奇,不值一提。
接下来是论文比较出彩的地方,如图4(b):
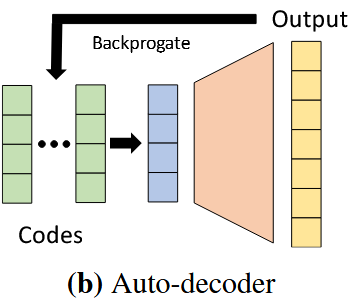
作者说,如果我们已经将一个DeepSDF模型训练好了,那么它理论上就可以表达一类模型的所有可能外观。因此当我们遇到一个没见过的这一类的模型,我们只需要找到该模型在这个训练好的网络的编号(潜向量)就可以了。因此,问题定位到怎么去找这个潜向量。作者提出了用一个Auto-decode模型来实现。具体的操作是,先随机生成一个潜向量,然后和已经知道SDF值的空间点一起扔进去模型得到一个预测SDF值,然后根据LOSS来调整潜向量以使得预测的SDF值与真实的SDF值尽可能靠近。
确定潜向量后,就可以拿这个模型来预测一些还不知道SDF值的点的SDF值了。这样就可以实现模型的重建和补全,如图6和图8:
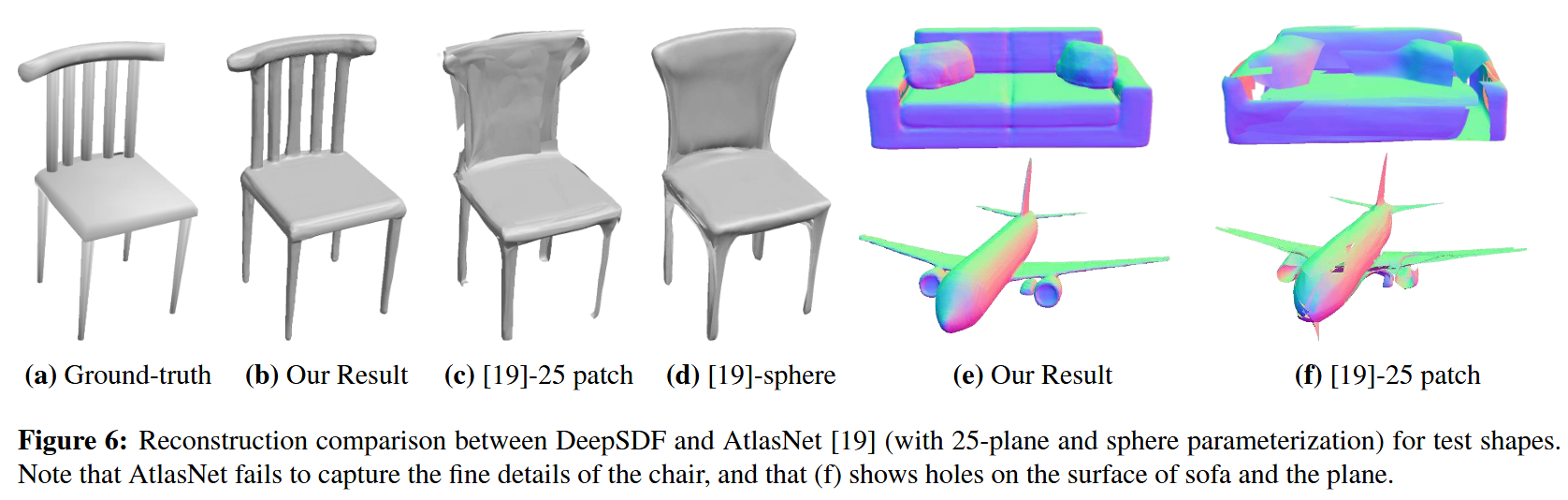
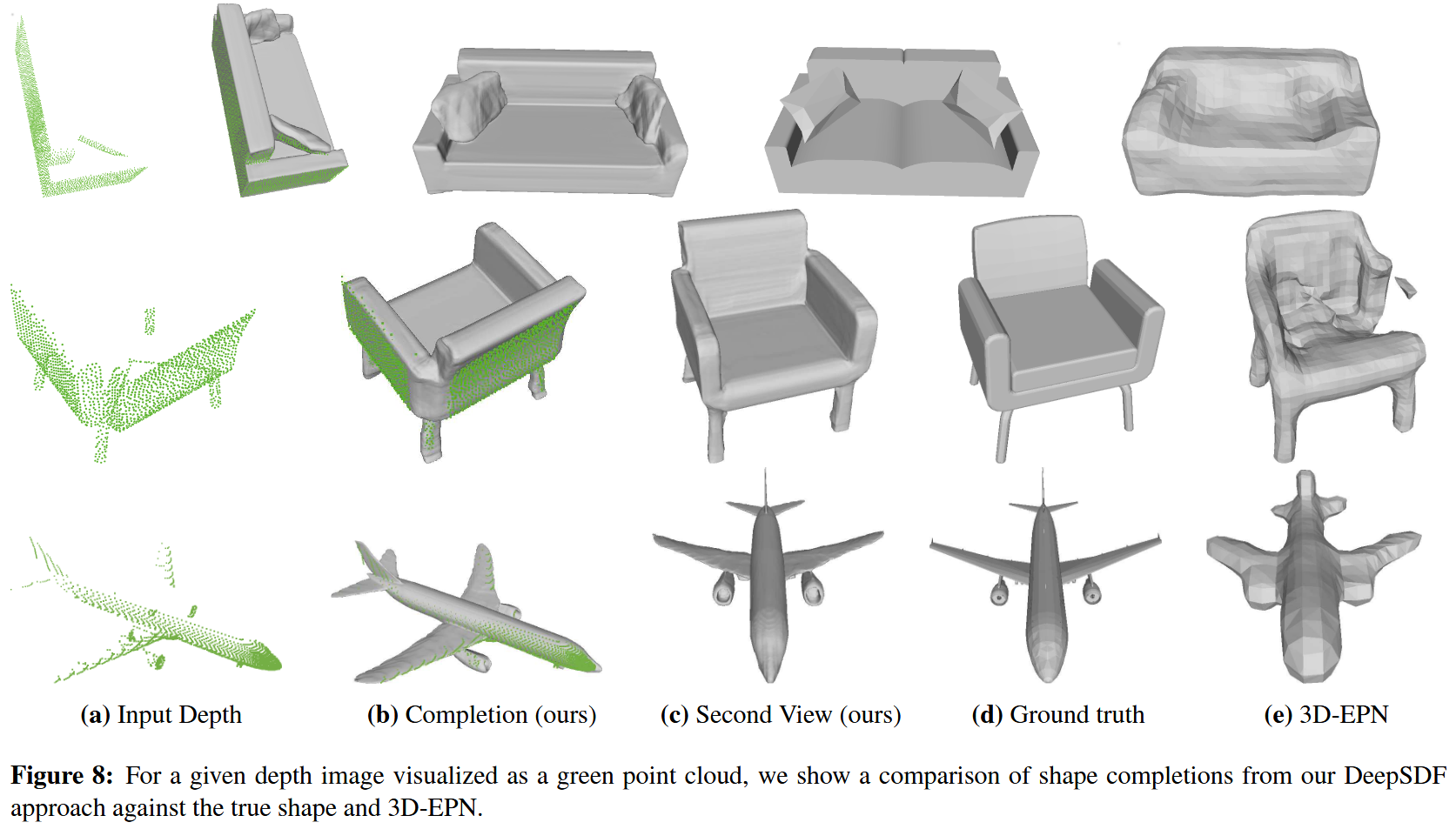
到此,原理解析就告一段落。值得一提的是,论文假设的情况比较理想,大多数时候,我们是不知道测试集的点的SDF值的。。。当然啦,总体还是瑕不掩瑜的。
代码实现
下面这部分我们将简要复现(或摘抄)一下DeepSDF的代码。
数据加载
这部分用于加载之前数据生成的npz文件,有一句说一句,npz文件的加载效率非常一般。如果有老哥希望提高训练效率,可能先改改这边的文件格式是好主意。数据加载的代码放在deep_sdf/data.py中,下面是本人稍作修改并加入注释的版本:
import logging
import numpy as np
import os
import random
import torch
import torch.utils.data# 遍历目录结构收集NPZ文件路径。数据集的划分信息写在一个JSON文件中,比如chairs分类写在"examples/splits/sv2_chairs_train.json"中
def get_instance_filenames(data_source, split):npzfiles = []for dataset in split:for class_name in split[dataset]:# 这里虽然写了for,但是实际上只会有一个数据集for instance_name in split[dataset][class_name]:instance_filename = os.path.join(dataset, class_name, instance_name + ".npz")if not os.path.isfile(os.path.join(data_source, instance_filename)):logging.warning("Requested non-existent file '{}'".format(instance_filename))npzfiles += [instance_filename]return npzfiles# 去除没有获取到SDF值的无用数据
def remove_nans(tensor):tensor_nan = torch.isnan(tensor[:, 3])#查看所有的第四列的值(也就是SDF值)是否为nan,是的话返回True,否则返回Falsereturn tensor[~tensor_nan, :]# 从NPZ文件中读取SDF样本
def unpack_sdf_samples(filename, subsample=None):npz = np.load(filename)if subsample is None:return npzpos_tensor = remove_nans(torch.from_numpy(npz["pos"]))neg_tensor = remove_nans(torch.from_numpy(npz["neg"]))half = int(subsample / 2) # 每个样本采集一半外部点和一半内部点# torch.rand(half)生成half个[0, 1)之间的随机数random_pos = (torch.rand(half) * pos_tensor.shape[0]).long()# 随机采样内部点random_neg = (torch.rand(half) * neg_tensor.shape[0]).long()sample_pos = torch.index_select(pos_tensor, 0, random_pos)sample_neg = torch.index_select(neg_tensor, 0, random_neg)# 拼接内部点和外部点samples = torch.cat([sample_pos, sample_neg], 0)return samplesdef read_sdf_samples_into_ram(filename):npz = np.load(filename)pos_tensor = torch.from_numpy(npz["pos"])neg_tensor = torch.from_numpy(npz["neg"])return [pos_tensor, neg_tensor]# 从内存中读取SDF样本
def unpack_sdf_samples_from_ram(data, subsample=None):if subsample is None:return datapos_tensor = data[0]neg_tensor = data[1]# split the sample into halfhalf = int(subsample / 2)pos_size = pos_tensor.shape[0]neg_size = neg_tensor.shape[0]pos_start_ind = random.randint(0, pos_size - half)sample_pos = pos_tensor[pos_start_ind : (pos_start_ind + half)]if neg_size <= half:random_neg = (torch.rand(half) * neg_tensor.shape[0]).long()sample_neg = torch.index_select(neg_tensor, 0, random_neg)else:neg_start_ind = random.randint(0, neg_size - half)sample_neg = neg_tensor[neg_start_ind : (neg_start_ind + half)]samples = torch.cat([sample_pos, sample_neg], 0)return samples# 定义SDFSamples类,继承自torch.utils.data.Dataset,以方便神经经网络训练时的数据加载
class SDFSamples(torch.utils.data.Dataset):def __init__(self, data_source, split, subsample, print_filename=False, num_files=1000000):self.subsample = subsample # 每个样本采样子集大小self.data_source = data_sourceself.npyfiles = get_instance_filenames(data_source, split) # 获取NPZ路径列表,传入参数为数据集地址和划分信息# 打印文件数量和数据源logging.debug("using " + str(len(self.npyfiles)) + " shapes from data source " + data_source)def __len__(self):return len(self.npyfiles)def __getitem__(self, idx):filename = os.path.join(self.data_source, self.npyfiles[idx])return unpack_sdf_samples(filename, self.subsample), idx
网络模型
网络模型部分官方代码为了可以参数化设置写的比较复杂,但网络结构非常简单。可以安装onnx,然后将模型导出为onnx格式进行可视化。操作如下:
pip install onnx
在networks/deep_sdf_decoder.py的末尾加入如下代码以导出模型:
import torch.onnx
if __name__ == "__main__":decoder = Decoder(latent_size = 256, # 潜在向量的维度dims = [512, 512, 512, 512, 512, 512, 512, 512], # 每层隐藏层的神经元数量,总共8层隐藏层dropout = [0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用dropoutdropout_prob = 0.2, # dropout概率norm_layers = [0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用归一化latent_in = [4], # 在这些层的输入中加入潜在向量weight_norm = True, # 使用权重归一化xyz_in_all = False, # 不在所有层的输入中加入xyz坐标use_tanh = False, # 不在输出层使用tanh激活函数latent_dropout = True # 在潜在向量上使用dropout)x = torch.randn(1, 259) # 随机生成一个输入torch.onnx.export(decoder, x, "model.onnx", input_names=["INPUT"], output_names=["OUTPUT"]) # 将 pytorch 模型以 onnx 格式导出并保存
最后用Netron导入保存的模型进行可视化:

可以看到,网络结构就是简单的全连接的叠加(代码在输入的时候将xyz和潜在向量进行分离,因此Netron中出现了Slice的模块,可以无视)。网络的输入为xyz坐标以及256个潜在向量(即同类对象中不同个体的词编码)的组合。
网络输入参数之后经过4个全连接层,全连接层的神经元个数除了首层外(输入层与输入个数相等,为259个)皆是512个。神经元的输出前三层也是512,最后一层为了可以和输入的259个数再次合并,降为253。经过4个全连接层之后,将输入与前4个全连接层合并之后再次输入到5层神经元中进行编码,最后一层输出SDF的值。
模型训练
模型训练代码放在train_deep_sdf.py中,整体流程可以说平平无奇,比较有意思的是其将潜在向量也进行了训练。本人一开始看论文的时候以为将实例与潜在向量对应起来之后潜在向量的值就不变了,直到看了代码才发现每个实例的训练都会更新其对应的潜在向量的值。这么做的好处应该是通过网络的学习将外形接近的实例的潜在向量值拉进,而明显不同的实例的潜在向量值推远。
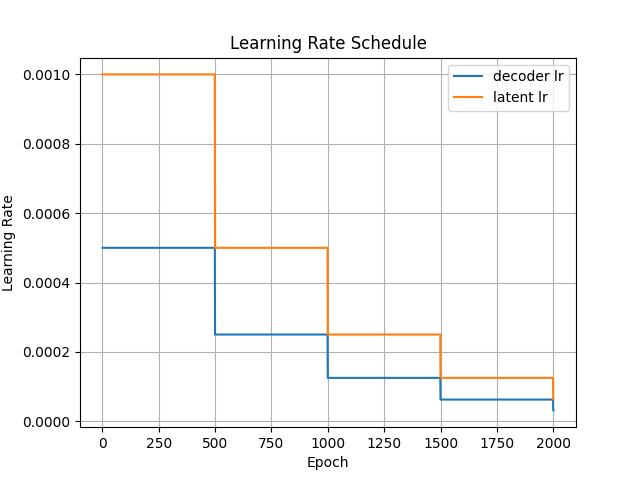
学习率设置
DeepSDF写了好几个类来封装学习率的设置,不过拆开来也就下面这两句代码。训练的时候更新的除了正常的网络参数外,还有一个个体对应的潜在向量值。
def get_learning_rate(initial, interval, factor, epoch):return initial * (factor ** (epoch // interval))
可视化出来如下图所示:
简化代码
为了更清晰的了解整个流程,这里对代码进行了简化。注意,这个代码虽然可以训练,但没有保存网络参数和潜在向量,如果有兴趣那这块代码进行训练需要加上。
import deep_sdf # 核心算法模块
import json
import logging
import torch
import torch.utils.data as data_utils # 数据加载工具
from tqdm import tqdm # 进度条显示
import time
import math
import networks.deep_sdf_decoder as network # 网络结构模块
import matplotlib.pyplot as plt######################### 学习率调度器 #########################
def get_learning_rate(initial, interval, factor, epoch):return initial * (factor ** (epoch // interval))loss_l1 = torch.nn.L1Loss(reduction="sum") # L1损失函数######################### 主程序 #########################
if __name__ == "__main__":logging.basicConfig(level=logging.DEBUG) # 设置日志输出级别为DEBUGdata_source = "data/SDFdata_train/SdfSamples"num_samp_per_scene = 16384#train_split_file = "examples/splits/sv2_planes_train.json"train_split_file = "examples/splits/sv2_planes_train_one.json"with open(train_split_file, "r") as f:train_split = json.load(f)sdf_dataset = deep_sdf.data.SDFSamples(data_source, train_split, num_samp_per_scene) # 创建SDF样本数据集类,实现数据集的加载和预处理# 创建适用于神经网络训练的数据加载器sdf_loader = data_utils.DataLoader(sdf_dataset,batch_size = 8, # 每个批次的场景数,设置为32shuffle = True, # 随机打乱数据num_workers = 8, # 多线程加载数据,设置为8drop_last = False, # 丢弃最后一个不完整的批次pin_memory = True, # 将数据加载到锁页内存中,提高数据传输速度)num_epochs = 2001 # 训练的总轮数start_epoch = 1 # 从第1轮开始训练# SDF值的截断距离,超过该距离的SDF值将被截断。这么做是为了防止极端值对训练产生不良影响,但也可能会丢失一些细节信息。# 比如一个点如果真的离表面很远,那么它的SDF值就会很大,如果我们把它截断到0.1,那么模型就无法学习到这个点的真实距离信息。# 这么做本人觉得不太靠谱,但这是DeepSDF的原始做法clamp_dist = 0.1 minT = -clamp_distmaxT = clamp_dist############# 设置神经网络 #############latent_size = 256 # 潜在向量的维度decoder = network.Decoder(latent_size = latent_size, # 潜在向量的维度dims=[512, 512, 512, 512, 512, 512, 512, 512], # 每层隐藏层的神经元数量,总共8层隐藏层dropout=[0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用dropoutdropout_prob=0.2, # dropout概率norm_layers=[0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用归一化latent_in=[4], # 在这些层的输入中加入潜在向量weight_norm=True, # 使用权重归一化xyz_in_all=False, # 不在所有层的输入中加入xyz坐标use_tanh=False, # 不在输出层使用tanh激活函数latent_dropout=True # 在潜在向量上使用dropout).cuda()############# 设置潜在向量 #############num_scenes = len(sdf_dataset)code_bound = 1.0 # 潜在向量的最大范数为1,约束潜在向量的范围# 创建一个可以学习的潜在向量矩阵,每个场景对应一个潜在向量lat_vecs = torch.nn.Embedding(num_scenes, latent_size, max_norm=code_bound).cuda()# 用均值为 0,标准差为 1.0 / sqrt(latent_size) 的正态分布,初始化潜在向量矩阵 lat_vecs 的权重# latent_size越大,则标准差越小,初始化的潜在向量越接近0。这个函数对每个场景都进行一次随机初始化torch.nn.init.normal_(lat_vecs.weight.data, 0.0, 1.0 / math.sqrt(latent_size))# lr = [{"Initial": 0.0005,"Interval": 500,"Factor": 0.5},# {"Initial": 0.001, "Interval": 500, "Factor": 0.5}]lr = [{"Initial": 2e-4,"Interval": 500,"Factor": 0.5},{"Initial": 1e-5, "Interval": 500, "Factor": 0.5}]# 设置优化器optimizer_all = torch.optim.Adam([{"params": decoder.parameters(),"lr": lr[0]["Initial"], # 设置参数的学习率为0.0005},{"params": lat_vecs.parameters(),"lr": lr[1]["Initial"], # 设置词向量的学习率为0.001},])# lr_history_0 = []# lr_history_1 = []for epoch in range(start_epoch, num_epochs + 1):# 记录每轮训练的开始时间start = time.time()decoder.train() # 确保模型启用训练模式(如激活Dropout和BatchNorm)# 调整学习率for i, param_group in enumerate(optimizer_all.param_groups):param_group["lr"] = get_learning_rate(lr[i]["Initial"], lr[i]["Interval"], lr[i]["Factor"], epoch) # 调整学习率# print(f"Epoch {epoch} learning rate for param group {i}: {param_group['lr']}")# # 记录学习率# if i == 0:# lr_history_0.append(param_group["lr"])# elif i == 1:# lr_history_1.append(param_group["lr"])loss_sum = 0.0 # 累计损失初始化为0# 创建进度条pbar = tqdm(total=len(sdf_loader), desc="Training Progress", unit="batch")for sdf_data, indices in sdf_loader: # 加载批次数据sdf_data = sdf_data.cuda()indices = indices.cuda()# 训练模型# sdf_data的形状是(B, N, 4),B是批次大小,N是每个场景的采样点数,4表示每个采样点的3D坐标和对应的SDF值# 这里我们并不关心数据在Batch维度上的划分,因此将其展平为(B*N, 4)形式sdf_data = sdf_data.reshape(-1, 4) # 将数据转换为(N,4)形式,前3列为坐标,第4列为目标值num_sdf_samples = sdf_data.shape[0] # 计算样本数量,即B*N=点数sdf_data.requires_grad = False # 不需要梯度计算。显式设置 requires_grad = False 可以确保 PyTorch 不会为它分配额外的计算资源用于梯度追踪,节省内存和计算。# 将xyz坐标和SDF值分开xyz = sdf_data[:, 0:3] # 3D坐标sdf_gt = sdf_data[:, 3].unsqueeze(1) # SDF真值sdf_gt = torch.clamp(sdf_gt, minT, maxT) # 限制SDF值范围optimizer_all.zero_grad() # 梯度清零# 获得对应的潜在向量# # indices.unsqueeze(-1)把 indices 从 (B,) 变成 (B, 1),增加一个维度。# .repeat(1, num_samp_per_scene)把每个场景编号在第二个维度上重复 num_samp_per_scene 次,得到 (B, num_samp_per_scene)。# .view(-1)把 (B, num_samp_per_scene) 展平为 (B * num_samp_per_scene,)。这样每个采样点都能对应到它所属场景的编号。indices = indices.unsqueeze(-1).repeat(1, num_samp_per_scene).view(-1) # 通过场景编号从潜在向量矩阵中获取对应的潜在向量latent_vec = lat_vecs(indices) # (B, N, latent_size)# 将潜在向量和坐标拼接作为网络输入 将潜在向量和xyz坐标拼接为输入inputs = torch.cat([latent_vec, xyz], 1)pred_sdf = decoder(inputs) # 前向传播pred_sdf = torch.clamp(pred_sdf, minT, maxT)# 限制预测的SDF值范围chunk_loss = loss_l1(pred_sdf, sdf_gt) / num_sdf_samplesl2_size_loss = torch.sum(torch.norm(latent_vec, dim=1))# 计算潜在向量的L2范数之和reg_loss = (1e-4 * min(1, epoch / 100) * l2_size_loss) / num_sdf_samples# 潜在向量正则化损失,随着训练进行逐渐增加。添加这个loss是为了防止潜在向量变得过大,从而影响模型的稳定性和泛化能力chunk_loss = chunk_loss + reg_loss.cuda()chunk_loss.backward() # 梯度反向传播optimizer_all.step() # 优化器更新参数。因为 PyTorch 的自动求导和优化器机制,需要先调用 backward() 计算梯度,然后再调用 step() 更新参数loss_sum += chunk_loss.item() # 累计损失,这里的 item() 是把张量转换为Python数值。为什么batch设置的不一样最后得到的值是一样的pbar.update(1)# update(1)表示进度条前进一步pbar.close()# 记录每轮训练的结束时间end = time.time()# 打印每轮训练时间print(f"Epoch {epoch} completed in {end - start:.2f} seconds.")# 打印每轮训练的平均损失print(f"Epoch {epoch} average loss: {loss_sum / len(sdf_loader):.6f}")# plt.plot(range(start_epoch, num_epochs + 1), lr_history_0, label='decoder lr')# plt.plot(range(start_epoch, num_epochs + 1), lr_history_1, label='latent lr')# plt.xlabel('Epoch')# plt.ylabel('Learning Rate')# plt.title('Learning Rate Schedule')# plt.legend()# plt.grid()# plt.show()
数据预测和可视化
这篇论文巧妙的地方主要集中在数据的预测部分,文章认为完成了模型训练,潜在向量配合网络就足够用来表达一类三维体,比如飞机。因此只要通过优化潜在向量的值,使得从某个飞机实例上采样得到的点(xyz)经过网络后的SDF值与真实SDF值尽可能接近,则优化后的潜在向量就可以直接描述该飞机。因为这个特性,网络即可以用来做点云的补全任务,又可以用来直接描述三维体(因为只需要点云和其对应的SDF真值,因此对该网络来说,所有任务本质上都是补全任务)。另外,只要传输双方都保有网络参数和结构,要传输一个三维体就只需要传输潜在向量这极小的值,三维体需要的存储、网络带宽资源将得到巨大的压缩。
这部分的实现内容比较简单,主要流程是:优化潜在向量→使用优化好的潜在向量进行三维重建
数据预测
第一部分代码比较简单,主要在reconstruct.py中,可将代码简化如下(这样一次只能重建一个对象,而且需要手动设置路径,好处就是看着比较简单):
import networks.deep_sdf_decoder as network # 网络结构模块
import logging
import time
import torch
import deep_sdf
import matplotlib.pyplot as plt# 进行三维重建的函数,返回最终的损失值和潜在向量。后续可以通过潜在向量进行三维重建
def reconstruct(decoder,# 网络模型num_iterations,# 迭代次数latent_size,# 潜在向量维度test_sdf,# SDF样本数据stat,# 潜在向量初始化的标准差clamp_dist,# SDF值截断距离num_samples=30000,# 每次迭代采样的点数lr=5e-4,# 学习率l2reg=False,# 是否使用L2正则化
):# 学习率调整函数#lr_history = []def adjust_learning_rate(initial_lr, optimizer, num_iterations, decreased_by, adjust_lr_every):lr = initial_lr * ((1 / decreased_by) ** (num_iterations // adjust_lr_every))#lr_history.append(lr)for param_group in optimizer.param_groups:param_group["lr"] = lrdecreased_by = 10 # 学习率衰减因子adjust_lr_every = int(num_iterations / 2) # 每多少次迭代调整一次学习率if type(stat) == type(0.1):latent = torch.ones(1, latent_size).normal_(mean=0, std=stat).cuda()# 用均值为0,标准差为stat的正态分布初始化潜在向量else:latent = torch.normal(stat[0].detach(), stat[1].detach()).cuda()# 用给定的均值和标准差初始化潜在向量latent.requires_grad = True # 需要计算潜在向量的梯度optimizer = torch.optim.Adam([latent], lr=lr)# 添加潜在向量作为优化器的参数loss_num = 0 # 记录损失值loss_l1 = torch.nn.L1Loss() # L1损失函数for e in range(num_iterations):decoder.eval() # 设置为评估模式,关闭dropout、批归一化等训练才开启的特性。sdf_data = deep_sdf.data.unpack_sdf_samples_from_ram(test_sdf, num_samples).cuda()# 获得待生成数据的采样点xyz = sdf_data[:, 0:3]# 提取xyz坐标sdf_gt = sdf_data[:, 3].unsqueeze(1)# 提取SDF真值,并增加一个维度以匹配网络输出sdf_gt = torch.clamp(sdf_gt, -clamp_dist, clamp_dist)# 限制SDF值范围在[-clamp_dist, clamp_dist]之间adjust_learning_rate(lr, optimizer, e, decreased_by, adjust_lr_every)# 调整学习率optimizer.zero_grad()# 梯度清零latent_inputs = latent.expand(num_samples, -1)# 扩展潜在向量以匹配采样点数量inputs = torch.cat([latent_inputs, xyz], 1).cuda()# 拼接潜在向量和坐标作为网络输入pred_sdf = decoder(inputs)# 前向传播pred_sdf = torch.clamp(pred_sdf, -clamp_dist, clamp_dist)# 限制预测的SDF值范围在[-clamp_dist, clamp_dist]之间loss = loss_l1(pred_sdf, sdf_gt)# 计算L1损失if l2reg: # 使用L2正则化loss += 1e-4 * torch.mean(latent.pow(2)) # L2正则化项,目的是防止过拟合。将潜在向量的值限制在较小范围内,避免过大或过小的值影响重建效果。loss.backward()# 反向传播计算梯度optimizer.step()# 优化器更新参数loss_num = loss.cpu().data.numpy()# 获取当前损失值# plt.plot(range(0, num_iterations), lr_history, label='latent lr')# plt.xlabel('Epoch')# plt.ylabel('Learning Rate')# plt.title('Learning Rate Schedule')# plt.legend()# plt.grid()# plt.show()return loss_num, latentif __name__ == "__main__":################# 网络模型加载 #################latent_size = 256decoder = network.Decoder(latent_size = latent_size, # 潜在向量的维度dims = [512, 512, 512, 512, 512, 512, 512, 512], # 每层隐藏层的神经元数量,总共8层隐藏层dropout = [0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用dropoutdropout_prob = 0.2, # dropout概率norm_layers = [0, 1, 2, 3, 4, 5, 6, 7], # 在这些层后面使用归一化latent_in = [4], # 在这些层的输入中加入潜在向量weight_norm = True, # 使用权重归一化xyz_in_all = False, # 不在所有层的输入中加入xyz坐标use_tanh = False, # 不在输出层使用tanh激活函数latent_dropout = True # 在潜在向量上使用dropout)################# 训练参数加载 #################saved_model_state = torch.load("examples/planes/ModelParameters/2000.pth")# 因为训练的时候官方用了DataParallel,所以参数字典的key前面会多一个"module."# 这里需要去掉才能加载到没有用DataParallel的模型中new_state_dict = {}for k, v in saved_model_state["model_state_dict"].items():new_key = k.replace("module.", "") if k.startswith("module.") else knew_state_dict[new_key] = vdecoder.load_state_dict(new_state_dict)decoder = decoder.cuda()################# 需要进行三维重建的文件加载 #################test_filename=r"G:\DeepSDF\Code\data\SDFdata_test\SdfSamples\ShapeNetV2\02691156\d6b4ad58a49bb80cd13ef00338ba8c52.npz"data_sdf = deep_sdf.data.read_sdf_samples_into_ram(test_filename)# 对内部点和外部点进行随机打乱重排data_sdf[0] = data_sdf[0][torch.randperm(data_sdf[0].shape[0])]data_sdf[1] = data_sdf[1][torch.randperm(data_sdf[1].shape[0])]################# 根据输入点云迭代潜在向量的值以使得sdf值尽可能接近真值 #################start = time.time()iterations=800 # 迭代次数默认为800次err, latent = reconstruct(decoder, int(iterations), latent_size, data_sdf, 0.01, 0.1, num_samples=8000, lr=5e-3, l2reg=True)decoder.eval()# 设置为评估模式,关闭dropout等################# 使用迭代完成的潜在向量值进行三维重建 #################mesh_filename=r"G:\DeepSDF\Code\examples\planes\Reconstructions\2000\d6b4ad58a49bb80cd13ef00338ba8c52_mesh.ply"start = time.time()with torch.no_grad():deep_sdf.mesh.create_mesh(decoder, latent, mesh_filename, N=256, max_batch=int(2 ** 18))logging.debug("total time: {}".format(time.time() - start))
学习率的调整细节如下:
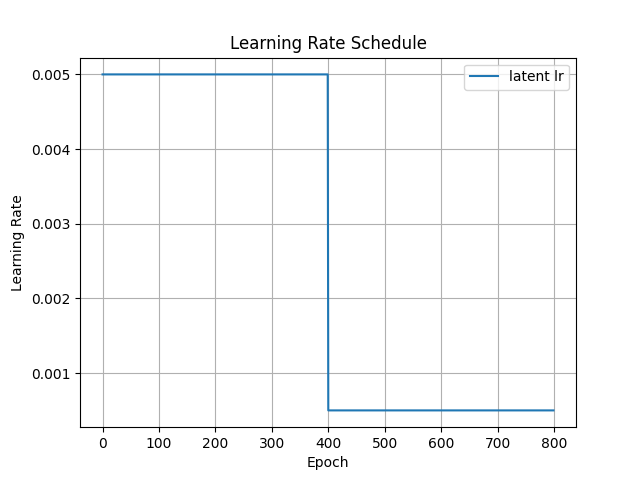
三维重建与可视化
使用优化好的潜在向量进行三维重建的代码放在metrics/mesh.py中。
主要的流程是创建256*256*256大小的体素,然后计算出这些体素的SDF值。得到SDF值之后直接交给skimage.measure.marching_cubes这个函数进行三维表面重建,该函数会根据输入的SDF值自动计算出三维体表面点和三角形索引。具体的算法因为和这篇论文没有关系就不展开了。
总结
到此我们对DeepSDF论文的解读,总的来说作为第一篇用神经网络进行SDF实现的论文表现是可圈可点的。虽然从现在的视角来看,除了潜在向量的自动解码操作比较有意思外,其他的操作比较直线,但第一个做的总归是牛逼的。
从实际应用的角度看,文章实现的效果处于不可用的状态,三维体重建存在着比较严重的不连续问题,需要后续研究的进一步改进。
