特殊矩阵的压缩存储
对于矩阵,我们可以很方便的用一维或者二维数组存储。还有一些特殊的矩阵,它们的存储需要一些其他的方法;
普通矩阵的存储

这是一个普通的矩阵,我们可以通过二维数组,一维数组或者是二维指针储存矩阵中的元素。但显然一维数组是最方便的最简洁的存储方式;
用一维数组存储矩阵中的数据有两种策略,第一种是行优先,一行一行的存储进数组。另一种是列优先,一列一列的将数据存进数组。两种策略没有什么区别,以下所有的内容都默认使用行优先
但是直接使用一维数组储存会存在一个弊端:不能直接通过二维数组的方式访问。不过也很好解决,只需要我们给矩阵元素的下标和储存数组的下标做一组映射即可:
- 假设我们将上面的矩阵存入了一维数组
B[m * n],如果我们要访问元素aij,根据下标可以计算出它是第i * n + j个储存进数组b的结果,所以访问B[i * n + j]即可- 根据这个规律就可以得到矩阵下标和数组下标之间的映射关系从而通过访问矩阵的方式查看储存在一维数组中的元素;
对称矩阵的压缩储存
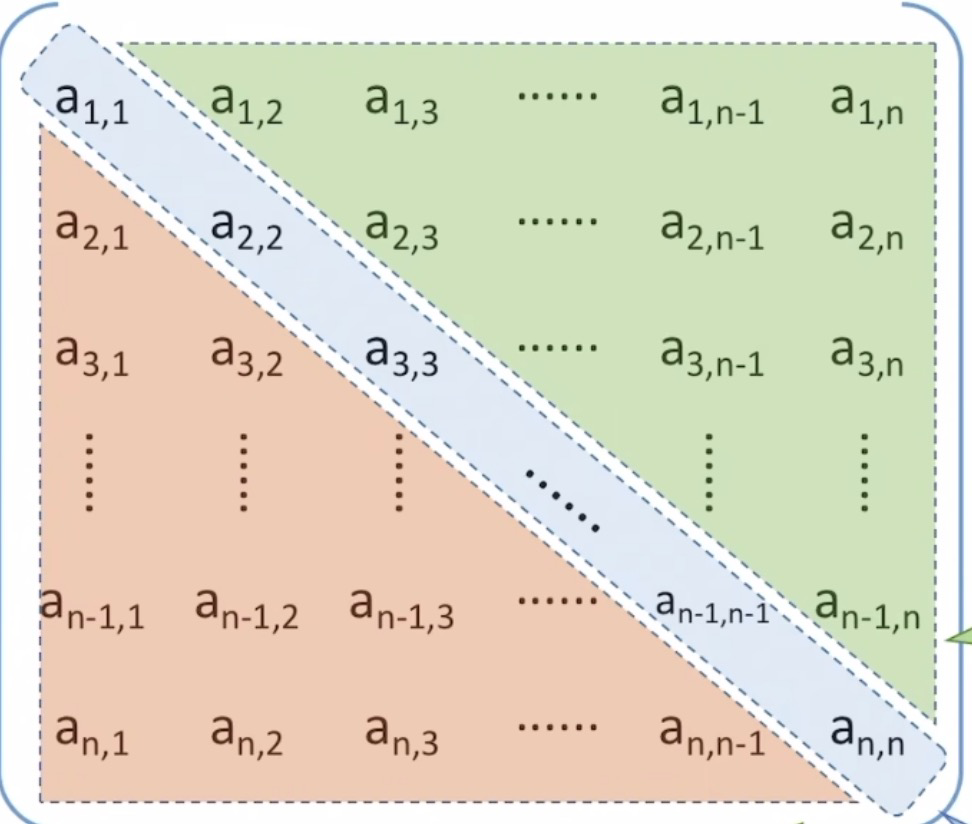
当矩阵中的元素都满足
aij = aji时就是一个对称矩阵,上下两个的三角形内对称的元素都是相等的,所以为了节省储存空间我们只需要储存其中一个三角形和对角线中的元素即可;
如何确定一维数组的规模:
- 只存储下三角区域和对角线区域,从上往下依次相加可以看到是满足等差数列的规律的,所以数组的规模为
n * (n - 1) / 2 * 数据类型的大小通过映射以二维数组的方式访问一维数组中的元素:
- 访问
aij时,除去本行前面每行依次有1, 2, ... , (i - 1)个元素,在本行中前面还有j - 1个元素,所以aij是第i * (i - 1) / 2 + j个进入数组的,访问一维数组下标为i * (i - 1) / 2 + j - 1的位置即可;- 如果需要访问
aji(j > i),根据对称性,访问B[i * (i - 1) / 2 + j]即可
三角矩阵的压缩存储
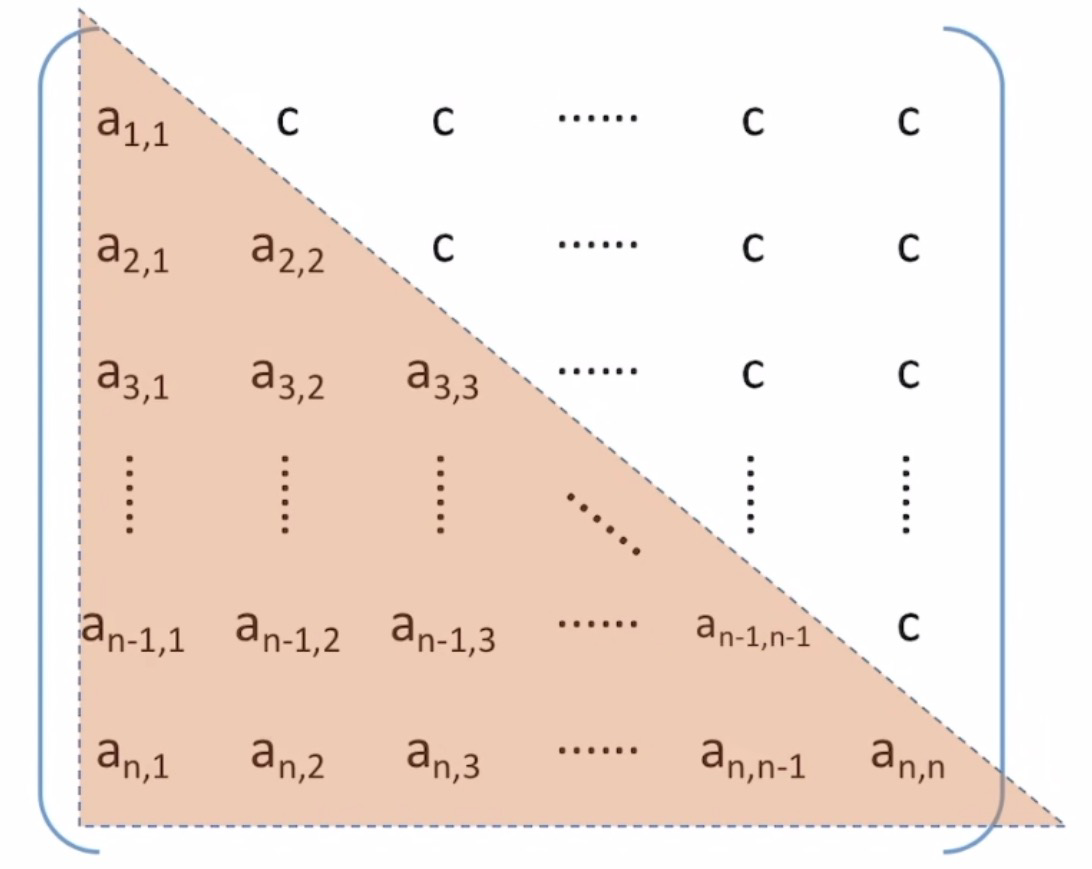
三角矩阵如图。可以说三角矩阵就是一个特殊的对称矩阵,只不过存储数组的规模会大一个对应数据类型的大小用来存储多出来的常数c;
访问下三角区域的方式和对称矩阵相同,而上三角矩阵即行标小于列标的位置只需要直接输出常数c即可;
三对角矩阵(带状矩阵)的压缩存储
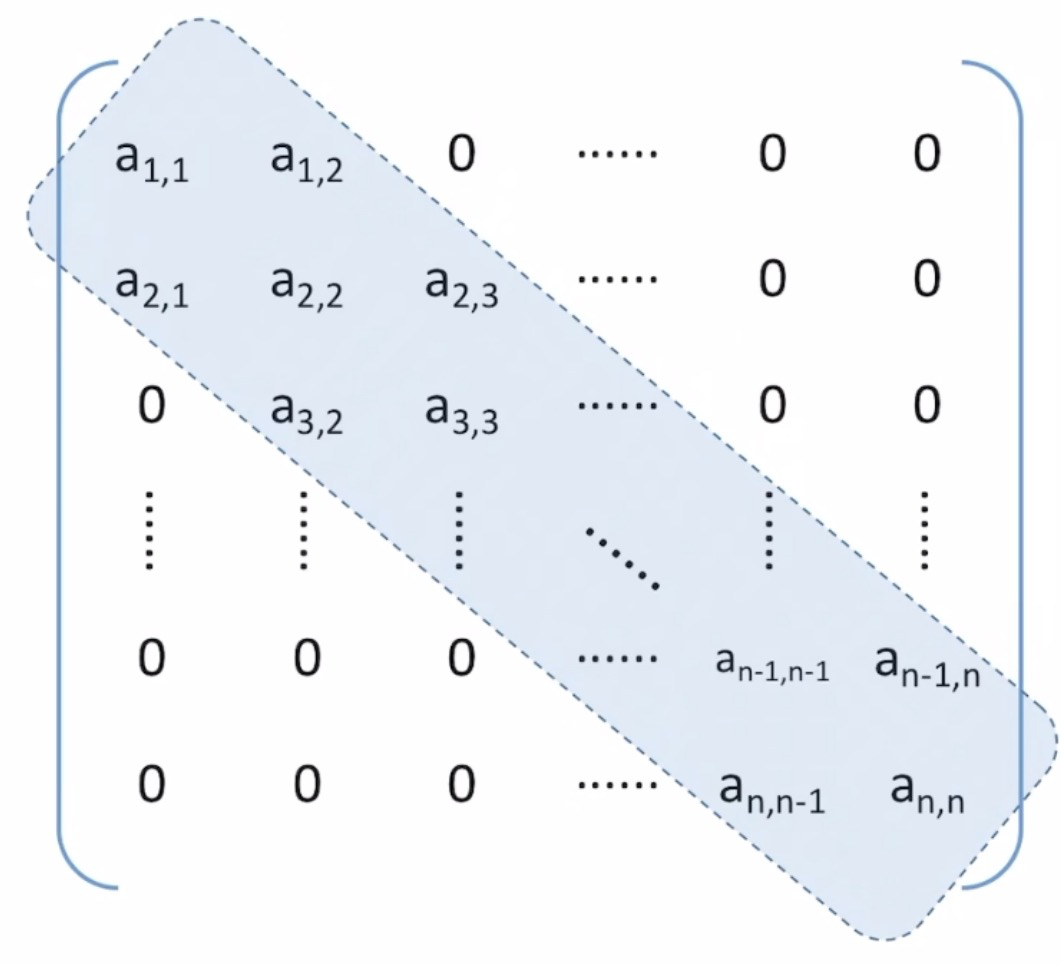
三对角矩阵如图所示。在该矩阵中除了行标和列标的差值的绝对值等于一的元素,其他元素全部为零;所以每一行我们只需要存储带状区域的元素。
存储数组的规模:
3n - 2,3n是指n行中每行有三个要存储的元素,-2是首尾行多算的两个;
矩阵下标与储存数组下标的映射关系(行优先原则):
aij对应数组中的第3 * (i - 1) - 1 + j - i + 1个元素,3 * (i - 1) - 1是算前面的几行的元素数量,j - i + 1是计算本行中在该元素前面的元素的数量,所以映射关系为:aij = B[2 * i + j - 3];- 行标和列标的关系不满足定义的则都为零;
已知
B[k],如何求aij?
- 根据定义,k + 1应该满足:
3 * (i - 1) - 1 < k + 1 <= 3 * i - 1;
则有(k + 2 ) / 3 + 1 > i >= (k + 2) / 3,可见不等式的两端距离只有1,而i又一定为整数,所以将(k + 2) / 3向上取整即可
稀疏矩阵的压缩存储

稀疏矩阵如图,该矩阵中的非零元素远远少于零元素,所以我们就只需要开辟空间储存非零元素即可。
策略一:
顺序存储
- 由于非零元素的出现是没有规律的,所以元素的行标和列标不能和一维数组的下标建立有效的映射关系。因此我们用链式结构来存储这些元素,要将元素的行标和列标一起储存
- 只需要定义节点
sturct Node{ int row; int col; value_type vlaue;}分别储存非零元素的行标,列标和值然后再定义Node类型的数组即可;
策略二:
十字链表法
- 相对于顺序存储,用链式结构存储将更加的方便并且即使没有映射关系也可以通过行标和列标再链表中定位元素;
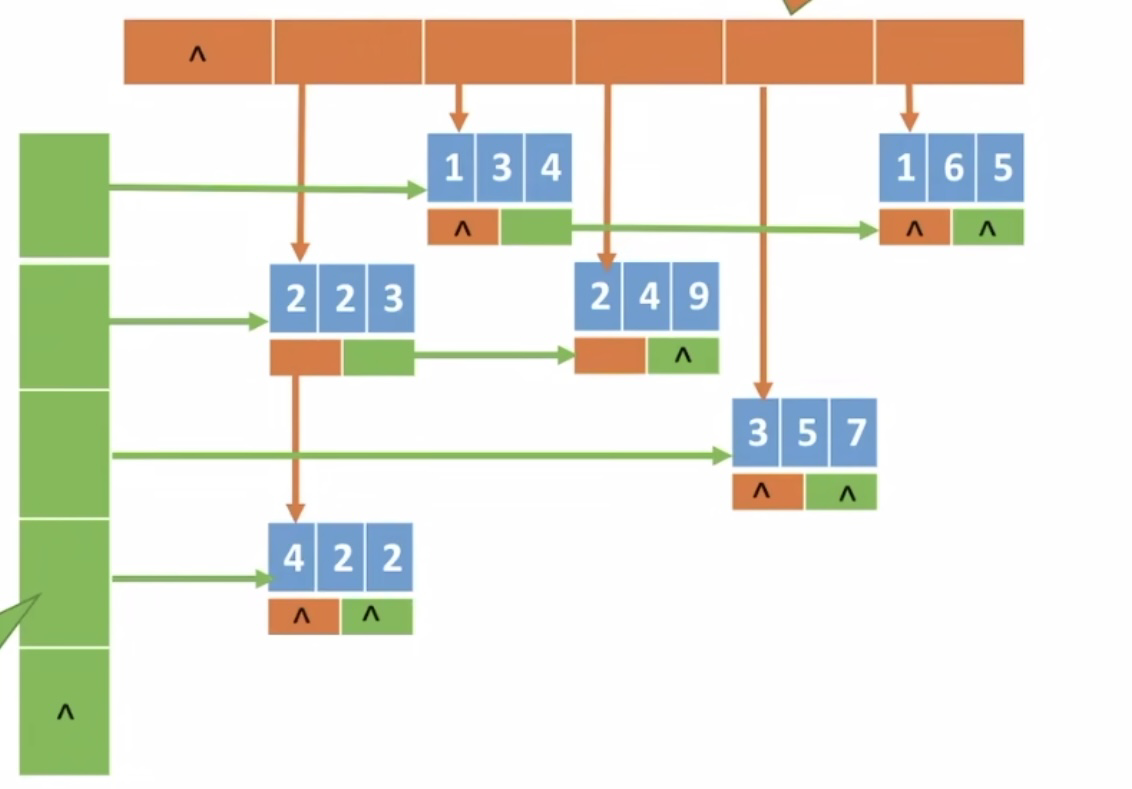
十字链表的结构如图,上边橙色和右边绿色的部分是链表的向下域和向右域;链表节点储存的内容:
- 行标
row,列标col,值value,同一列下一个元素的地址down,同一行下一个元素的地址right;遍历某一行或者某一列的方法:
- 向下域中的每一个节点中都存储着本列第一个元素的地址,通过该地址遍历即可;
同样的向右域则储存了本行中第一个元素的地址,以此遍历即可;通过行列号定位某个结点的方法
- 先通过向下域中的节点定位到对应的列标,然后遍历该列的元素,找到行标
row符合要求的即可;- 如果先定位行通过向右域遍历再找对应的列标即可;
总结:
- 十字链表储存相对于用普通的链表储存来说可以进行行遍历和列遍历,更符合矩阵的功能需求;
- 十字链表的向下域和向右域实际上也是两个链表,它们结点的个数和矩阵的行列数相同,它们的功能相当于直角坐标系;