算法题（219）：纪念品

审题：
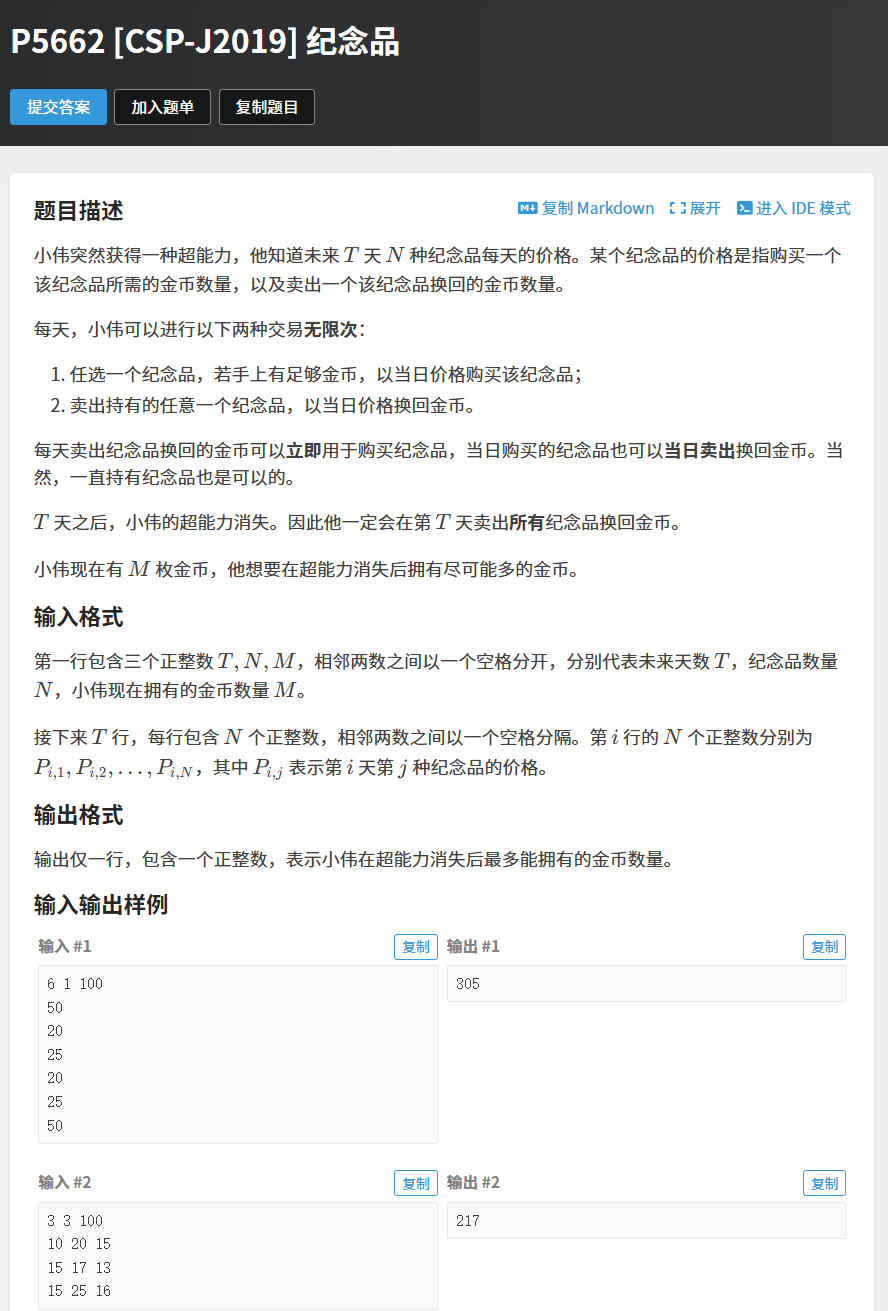
本题需要我们帮助小伟根据股票1~t天的股票价格进行操作，最终在第t天获得最多金币

思路：
方法一：贪心+动态规划

本题的股票交易分为两种：

情况1：隔天操作

情况2：隔n天操作

但是其实我们可以将情况2看成进行“多次”隔天操作，题目中允许当天买当天卖

eg：

我们看到将第一天买，第四天卖转化成：
1：买

2：卖+买

3：卖+买

4：卖

且由于第二天和第三天的买卖价值一样，所以2,3天对利润没有任何影响

综上：某天买，多天后卖 == 某天买，隔天卖（循环进行）

贪心策略：

由于此时已经将跨天卖归并到隔天卖了，所以我们只需要考虑某天买隔天卖的情况

当隔天卖可以赚钱，我们就买，否则不买，也就是每次情况都要是最优的，所以我们对每种情况都遍历进行判断

动态规划：
考虑到这里有多件不限量股票（物品数量），且本金有限（限定条件），所以本题也属于完全背包问题

（1）状态表示：

f[i][j]表示当天在1~n范围内选择若干股票购买，在总消耗金额不超过m的情况下，第二天卖出后所能获得的最大利润

（2）状态转移方程：
情况1：不购买第i个股票

f[i][j] = f[i-1][j]

情况2：购买第i个股票

f[i][j] = f[i][j-v[i]] + w[i]-v[i]

注意只有j >= v[i]的时候才有情况2

（3）初始化：
都初始化为0即可，但是由于我们的动态规划是需要进行多次的，所以dp数组f需要进行数据清空

（4）填表顺序：
状态转移方程依赖于上一行以及当前行的左侧数据，所以从上到下，从左到右进行填表

（5）答案输出：
直接返回m+f[n][m]，因为最终返回的是拥有的金币数量（当期利润加本金）

（6）空间优化：
本题的是完全背包，且限定条件是小于等于

故：降维后仍按照从上到下，从左到右填表

解题：
 

#include<iostream>
#include<cstring>
using namespace std;
const int N = 110, M = 1e4 + 10;
int t, n, m;
int p[N][N];
int f[M];
int solve(int v[], int w[], int m)//返回操作完这一次操作后的总剩余金额
{memset(f, 0, sizeof f);//多组处理，清空残余数据for (int i = 1; i <= n; i++){for (int j = v[i]; j <= m; j++){f[j] = max(f[j], f[j - v[i]] + w[i] - v[i]);}}return m + f[m];
}
int main()
{//数据录入cin >> t >> n >> m;for (int i = 1; i <= t; i++){for (int j = 1; j <= n; j++){cin >> p[i][j];}}//贪心策略：每次交易都要最优for (int i = 1; i < t; i++){m = solve(p[i], p[i + 1], m);}//答案输出cout << m << endl;return 0;
}

P5662 [CSP-J2019] 纪念品 - 洛谷