数据结构——基本排序算法
目录
前言
一、基本概念
二、排序算法的性能分析
三、排序算法的种类
1、插入算法
(1)核心思路
(2)图解
(3)示例代码
2、冒泡排序
(1)核心思路
(2)图解
(3)示例代码
3、选择排序
(1)核心思路
(2)图解
(3)示例代码
4、快速排序
(1)核心思路
(2)图解
(3)示例代码
5、希尔排序
(1)核心思路
(2)图解
(3)示例代码
前言
在计算机科学的世界里,排序是一项无处不在、至关重要的基础操作。无论是数据库索引的快速查询,还是社交媒体的信息流展示,抑或是电商网站的商品列表,其背后都离不开高效排序算法的支撑。排序算法的优劣,直接决定了程序的响应速度和资源消耗,是衡量程序员内功深浅的重要标尺。
本篇文章将带领大家踏入排序算法的殿堂,聚焦于那些最经典、最常用的基本排序算法。我们从最直观的“冒泡排序”和“选择排序”入手,理解算法是如何一步步通过比较和交换来让数据变得有序;然后探讨“插入排序”,体会它在处理“近乎有序”数据时的惊人效率。我们不仅会探讨它们的思路和实现,更会深入分析其时间/空间复杂度,并通过生动的图解来化解理解上的难点。
理解这些“基础”算法并非只是为了解决特定的问题,更重要的是,它们蕴含着分治、递归、增量处理等核心算法思想,是通往更高级算法(如快速排序、归并排序、堆排序)的必经之路。让我们从这些基石开始,一起揭开算法效率背后的奥秘。
一、基本概念
说明:
排序是计算中最基础、最核心的数据处理操作之一。其目的非常直观:将一组“无序”的数据元素序列,按照某个特定的规则重新排列,使其成为“有序”的序列。
这里的关键在于“特定的规则”,通常它指的是数据元素中某个可比较的字段(也称为关键字)。例如,一个学生数据节点可能包含学号、姓名、成绩等多个字段。我们可以选择学号作为关键字进行升序排序,也可以选择成绩作为关键字进行降序排序。排序算法的任务,就是根据指定的关键字,高效地完成重新排列。
稳定性:
稳定性是衡量排序算法特性的一个重要指标,它的定义如下:
在一组待排序的序列中,如果存在两个或多个具有相同关键字的数据元素,在排序完成之后,这些相等元素的相对位置(即它们原本的先後顺序)保持不变,那么我们就称这个排序算法是稳定的;反之,则称为不稳定的。
举例说明:
假设我们有一组学生数据,需要按“成绩”排序,但原始顺序中成绩同为90分的张三在李四之前。如果排序后,张三依然排在李四之前,则该算法稳定;如果李四可能排到张三之前,则该算法不稳定。在某些场景下(例如先按成绩排序,再按学号排序),稳定性至关重要。
内排序和外排序:
根据排序算法过程中数据存放的位置,排序算法可分为两类:
内排序:
指待排序的所有数据可以一次性全部加载到计算机的内存中进行处理的排序算法。这是我们平时讨论最多的排序方式,适用于数据量不大的情况
外排序:
当数据量非常庞大,以至于无法全部放入内存时,就需要使用外排序。这类算法需要将数据分批次地从外部存储器(如硬盘)读入内存进行处理,中间结果再写回外部存储。外排序的核心是“归并”思想,通常涉及内存与外部存储之间复杂的数据交换。
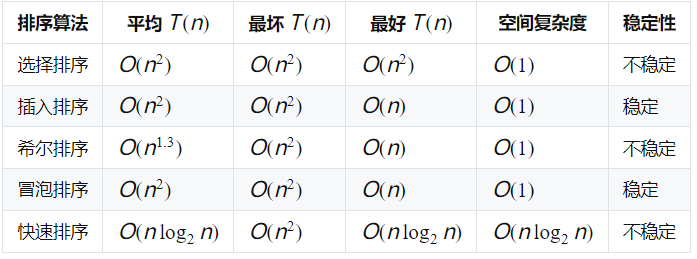
二、排序算法的性能分析
我们可以得到一些简单的思路指导:
简单排序算法(选择排序、插入排序、冒泡排序):
-
特点: 思路直观易懂,是学习算法思想的良好入门。
-
性能: 它们的平均和最差时间复杂度均为 O(n²),这意味着当数据量n增大时,效率会显著下降。因此,它们仅适用于数据样本量非常小(例如 n < 100)的场合。
-
优势: 一个显著的共同优点是空间效率高。它们通常只需要常数级别的额外空间(即空间复杂度为 O(1)),属于“原地排序”,不需要额外开辟大量内存。
希尔排序:
-
特点: 希尔排序是插入排序的改进版,它通过引入“增量”序列,对数据进行分组预排序,使得元素能够大跨度地移动,从而有效减少了后续直接插入排序的工作量。
-
性能: 它的时间复杂度分析较为复杂,但在平均情况下的性能远优于简单的 O(n²) 算法,介于 O(n log n) 和 O(n²) 之间。它同样是一种原地排序算法。
-
注意: 希尔排序是一种不稳定的排序算法。
快速排序:
-
特点: 快排采用了分治策略,是目前实践中平均性能最优越的排序算法之一。
-
性能: 其平均时间复杂度为 O(n log n),效率非常高。
-
代价: 这种高效率的代价是对内存空间的消耗。由于快排通常通过递归实现,在数据量非常大时,递归调用栈会消耗较多的内存空间(平均空间复杂度为 O(log n),最坏情况下为 O(n))。因此,当数据量极大而内存资源紧张时,需要权衡这一因素。
三、排序算法的种类
1、插入算法
(1)核心思路
算法可以形象地理解为:对于一个序列,我们总是维护一个位于序列前端的有序子序列。开始时,这个有序子序列只包含第一个元素(单个元素自然有序)。
初始状态: 将数组的第一个元素视为一个已排序的序列。
遍历插入: 从第二个元素(索引
i = 1)开始,将其视为待插入的新牌。寻找位置并插入: 将待插入元素与它前面的有序序列从后向前逐一比较,找到第一个不大于它的元素,并将其插入到该位置之后。在这个过程中,比待插入元素大的元素都需要依次向后移动一位,为它腾出空间。
重复过程: 重复步骤2和3,直到最后一个元素也被插入到前面的有序序列中,整个数组排序完成。
简单来说:
假设数组前 i 个元素已经有序,那么我们的任务就是将第 i+1 个元素插入到这个有序序列的合适位置。由于第一个元素自身就是有序的,因此我们从第二个元素开始,不断地将新元素插入到前面的有序序列中,直到整个数组有序。
(2)图解
假设总共有n个节点,那么总共需要将n-1节点插入到有序序列中,而插入节点时需要找到合适地位置,显然这个查找的过程的时间复杂度是O(n-i),因此插入排序的时间复杂度是O(n-1)(n-1),即O(n的2次方)
(3)示例代码
/********************************************************************************* @file insert_sort.c* @author feng* @version V0.0.1* @date 2025.09.26* @brief 插入排序的实现* ******************************************************************************* @attention** 本文档只供装逼学习使用,不得商用,违者必究** github: https://github.com/(求我拿链接)* CSDN: https://blog.csdn.net/(嘻嘻)* gitee: https://gitee.com/(求我拿链接)* 微信公众号: 测试中....* 有疑问或者建议:1740219515@qq.com** *******************************************************************************/#include <stdio.h>
#include <time.h>
#include <stdlib.h>/*** @brief 获取随机数,并返回* @note None* @param size: rand函数随机数范围的最大值* @retval 成功:返回获取到的随机数的值* 失败:返回-1*/
int INSERTION_SORT_RandNum(int size)
{if (size>32767){return -1;}return rand() % (size+1);}/*** @brief 显示数据* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval */
void INSERT_SORT_SHOW(int *data_p,int len)
{for (int i = 0; i < len; i++){printf("%d ",*(data_p+i));}printf("\n");
}/*** @brief 插入排序* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval */
void INSERT_SORT(int *data_p,int len)
{if (len<1){return;}int tmp_data=0;int i=0;int j=0;for (i = 1; i < len; i++){tmp_data=data_p[i];for (j = i-1; j >=0; j--){if (tmp_data<data_p[j]){data_p[j+1]=data_p[j];}else{break;}}data_p[j+1]=tmp_data;}}int main(int argc, char const *argv[])
{srand(time(NULL));int test_data[128];for (int i = 0; i < sizeof(test_data)/sizeof(test_data[0]); i++){test_data[i] = INSERTION_SORT_RandNum(100);}printf("随机序列: \n");INSERT_SORT_SHOW(test_data, sizeof(test_data)/sizeof(test_data[0]));printf("插入排序: \n");INSERT_SORT(test_data, sizeof(test_data)/sizeof(test_data[0]));INSERT_SORT_SHOW(test_data, sizeof(test_data)/sizeof(test_data[0]));return 0;
}
2、冒泡排序
(1)核心思路
冒泡排序是最基础和直观的排序算法之一,其名称源于排序过程中,较小的(或较大的)元素会经由交换慢慢“浮”到数列的顶端,如同水中的气泡一样。
在深入算法之前,我们先明确两个关键概念:
顺序: 如果序列中两个数据的位置关系符合最终的排序要求(例如,在升序排序中,前面的元素小于等于后面的元素),则称这两个数据是顺序的。
逆序: 如果序列中两个数据的位置关系不符合最终的排序要求(例如,在升序排序中,前面的元素大于后面的元素),则称这两个数据是逆序的。
排序算法的核心工作,就是通过一系列操作,消除序列中的所有逆序对。
冒泡排序的思路非常直接:重复地遍历待排序序列,一次比较两个相邻元素,如果它们是逆序的,就交换它们的位置。
初始状态: 整个序列为待排序区域。
单轮冒泡: 从序列的起始位置开始,比较每一对相邻元素。如果它们的顺序错误(即逆序),就交换它们。这一轮遍历结束后,当前待排序区域中最大(或最小)的元素就像气泡一样“冒”到了正确的位置(序列末端)。
缩小待排序区域: 此时,序列末尾的元素已经有序,将其排除在下一轮的待排序区域之外。
重复过程: 重复步骤2和3,每次遍历都会将当前待排序区域中的极值元素归位。直到在某一次遍历中,没有发生任何元素交换,说明序列已经完全有序,排序结束。
简单来说: 通过相邻元素的两两比较和交换,在每一轮中将一个极值元素归位,直到整个序列有序。
(2)图解
假如序列中有n个数据,那么在最极端情况下,只需要经过n-1轮的比较,则一定可以将所有的数据排序完毕,冒泡排序的时间复杂度O(n的2次方)
(3)示例代码
/********************************************************************************* @file babble_sort.c* @author feng* @version V0.0.1* @date 2025.09.26* @brief 冒泡排序的实现* ******************************************************************************* @attention** 本文档只供装逼学习使用,不得商用,违者必究** github: https://github.com/(求我拿链接)* CSDN: https://blog.csdn.net/(嘻嘻)* gitee: https://gitee.com/(求我拿链接)* 微信公众号: 测试中....* 有疑问或者建议:1740219515@qq.com** *******************************************************************************/#include <stdio.h>
#include <time.h>
#include <stdlib.h>/*** @brief 获取随机数,并返回* @note None* @param size: rand函数随机数范围的最大值* @retval 成功:返回获取到的随机数的值* 失败:返回-1*/
int BUBBLE_SORT_RandNum(int size)
{if (size>32767){return -1;}return rand() % (size+1);}/*** @brief 显示数据* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval */
void BUBBLE_SORT_SHOW(int *data_p,int len)
{for (int i = 0; i < len; i++){printf("%d ",*(data_p+i));}printf("\n");
}/*** @brief 冒泡排序* @note None* @param data_p:指向要排序数据内存的指针* len:数据的内存长度* @retval 成功:返回0* 失败:返回-1*/ int BUBBLE_SORT(int *data_p,int len)
{if ((data_p==NULL)||(len<=1)){return -1;}int i=0;int j=0;int temp=0;for (i = 0; i < len-1; i++){for ( j = 0; j < len-1-i; j++){if (data_p[j]>data_p[j+1]){temp=data_p[j];data_p[j]=data_p[j+1];data_p[j+1]=temp;}}}return 0;
}int main(int argc, char const *argv[])
{srand(time(NULL)); int test_data[128]={0};for (int i = 0; i < sizeof(test_data)/sizeof(test_data[0]); i++){test_data[i] = BUBBLE_SORT_RandNum(100);}printf("数据:\n");BUBBLE_SORT_SHOW(test_data,sizeof(test_data)/sizeof(test_data[0]));printf("冒泡排序:\n");BUBBLE_SORT(test_data,sizeof(test_data)/sizeof(test_data[0]));BUBBLE_SORT_SHOW(test_data,sizeof(test_data)/sizeof(test_data[0]));return 0;
}
3、选择排序
(1)核心思路
选择排序是一种直观易懂的排序算法,其核心思想是:不断地从待排序序列中选出最小(或最大)的元素,将其放到已排序序列的末尾。与我们平时按身高排队时,每次从队伍中选出最矮的人排到最前面的思路如出一辙。
算法的执行过程可以清晰地分为以下几个步骤:
初始状态: 整个序列为待排序区域,已排序区域为空。
寻找极值: 在当前的待排序区域中,从头到尾遍历一遍,找到其中最小(升序排序)或最大(降序排序)的元素。
放置元素: 将找到的这个极值元素,与待排序区域的第一个元素进行交换。此时,这个极值元素就被放置在了其最终的正确位置上。
缩小区域: 此时,序列前端的这个元素已经有序,将其纳入已排序区域。待排序区域随之缩小。
重复过程: 重复步骤2至4,每次都为缩小的待排序区域找到一个新的极值元素并归位。直到待排序区域只剩下一个元素时,整个序列就已经有序了。
简单来说: 它的策略就是“选择-交换-缩小”,依次从头到尾挑选合适的元素放到序列的前面。
(2)图解
如果总共有n个节点,那么选择一个合适的节点需要比较n次,因此总的时间复杂度O(n的2次方)
(3)示例代码
/********************************************************************************* @file select_sort.c* @author feng* @version V0.0.1* @date 2025.09.26* @brief 选择排序的实现* ******************************************************************************* @attention** 本文档只供装逼学习使用,不得商用,违者必究** github: https://github.com/(求我拿链接)* CSDN: https://blog.csdn.net/(嘻嘻)* gitee: https://gitee.com/(求我拿链接)* 微信公众号: 测试中....* 有疑问或者建议:1740219515@qq.com** *******************************************************************************/#include <stdio.h>
#include <time.h>
#include <stdlib.h>/*** @brief 获取随机数,并返回* @note None* @param size: rand函数随机数范围的最大值* @retval 成功:返回获取到的随机数的值* 失败:返回-1*/
int SELECT_SORT_RandNum(int size)
{if (size>32767){return -1;}return rand() % (size+1);}/*** @brief 显示数据* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval None*/
void SELECT_SORT_SHOW(int *data_p,int len)
{for (int i = 0; i < len; i++){printf("%d ",*(data_p+i));}printf("\n");
}/*** @brief 选择排序* @note None* @param data_p:指向要排序数据内存的指针* len:数据的内存长度* @retval 成功:返回0* 失败:返回-1*/ int SELECT_SORT(int *data_p,int len){if ((data_p==NULL) || (len<=0)){return -1;}int i=0;int j=0;int temp=0;int min_num=0;for ( i = 0; i < len; i++){min_num=i;for ( j = i; j < len; j++){if (data_p[j]<data_p[min_num]){min_num=j;}}if (min_num!=i){temp=data_p[i];data_p[i]=data_p[min_num];data_p[min_num]=temp;}}return 0;
}int main(int argc, char const *argv[])
{srand(time(NULL)); int test_data[128]={0};for (int i = 0; i < sizeof(test_data)/sizeof(test_data[0]); i++){test_data[i] = SELECT_SORT_RandNum(100);}printf("排序前:\n");SELECT_SORT_SHOW(test_data,sizeof(test_data)/sizeof(test_data[0]));SELECT_SORT(test_data,sizeof(test_data)/sizeof(test_data[0]));printf("排序后:\n");SELECT_SORT_SHOW(test_data,sizeof(test_data)/sizeof(test_data[0]));return 0;
}4、快速排序
(1)核心思路
快速排序是当今实践中最快、应用最广泛的通用排序算法之一。它由Tony Hoare于1960年提出,其核心是分治策略。正如您所说,虽然它是一种递归算法,需要额外的栈空间,但其语句执行频度(即平均时间复杂度)在比较排序算法中是最优的,因此理论上的时间效率最高。
快速排序的流程可以概括为三个步骤:选择支点 -> 划分 -> 递归。
选择支点:
从待排序序列中任意选取一个数据作为基准元素,称为 "支点"。选择策略可以很简单(如总是选第一个元素),也可以很复杂(如三数取中法)。
划分:
这是快速排序的核心操作。目标是重新排列序列,使得所有比支点小的元素都放在支点的左边,所有比支点大的元素都放在支点的右边。操作结束后,支点就处于其最终的正确位置上。
这个操作称为 "一次划分"。
递归:
一次划分之后,序列呈现出一种基本有序的状态:支点左子序列 < 支点 < 支点右子序列。虽然左右两个子序列内部可能是无序的,但我们可以将它们视为两个独立的、规模更小的排序问题。
然后,递归地将相同的算法应用于左子序列和右子序列。
递归基: 当子序列的长度小于等于1时,它自然就是有序的,递归终止。
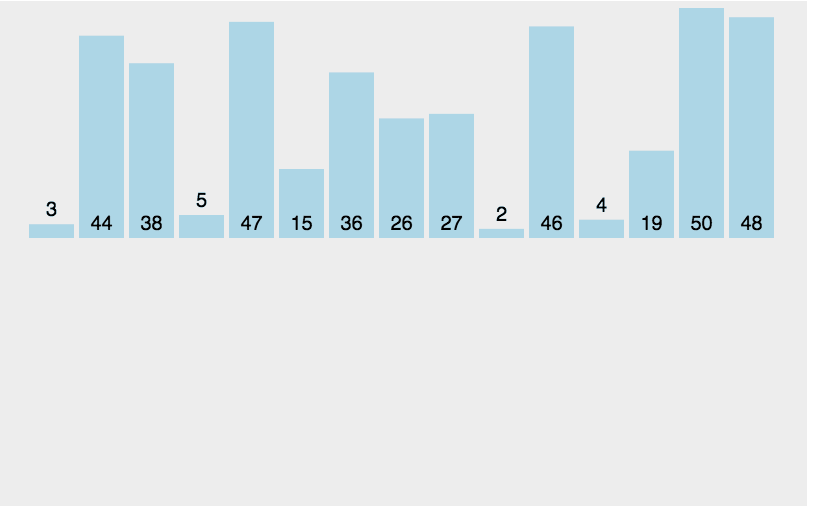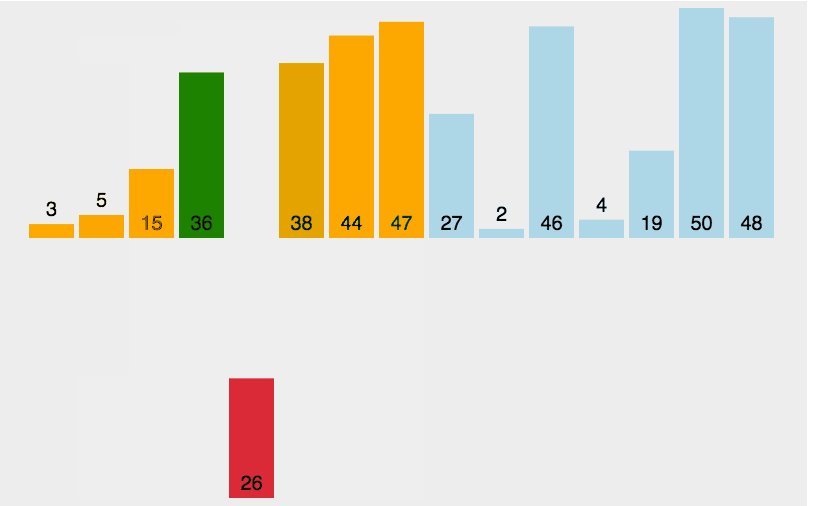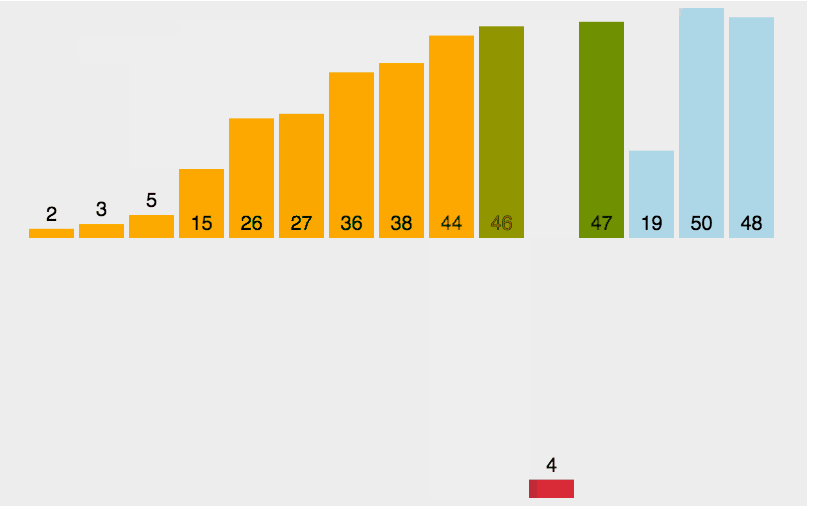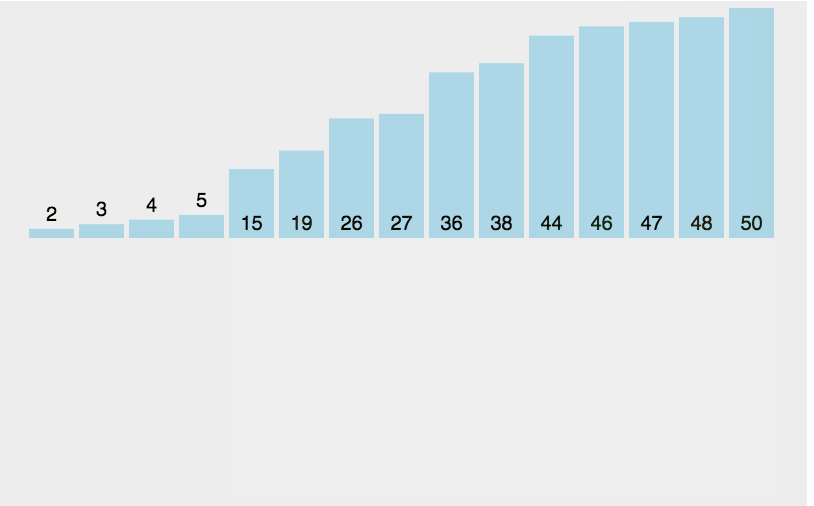
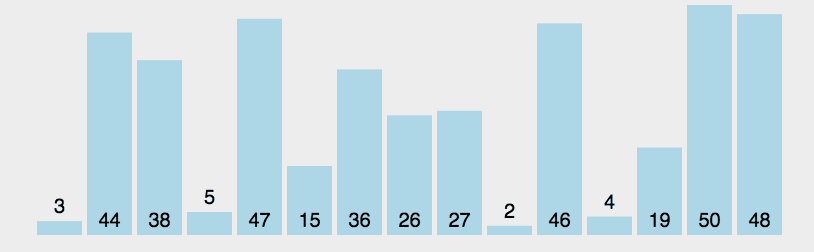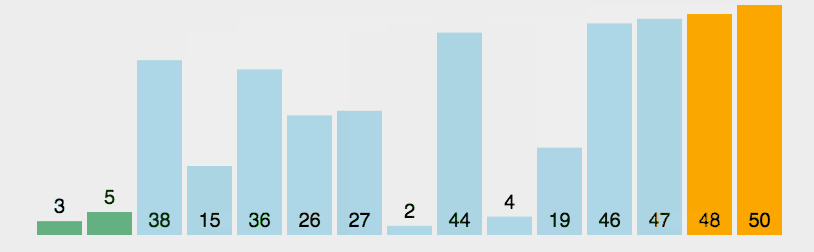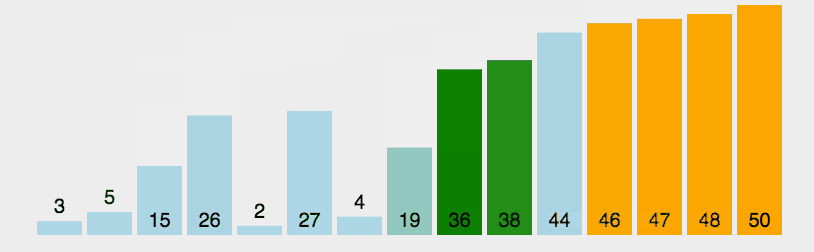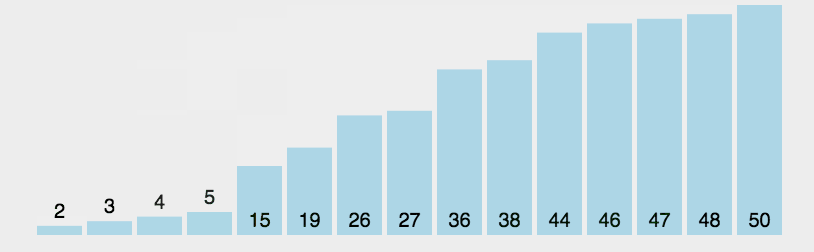
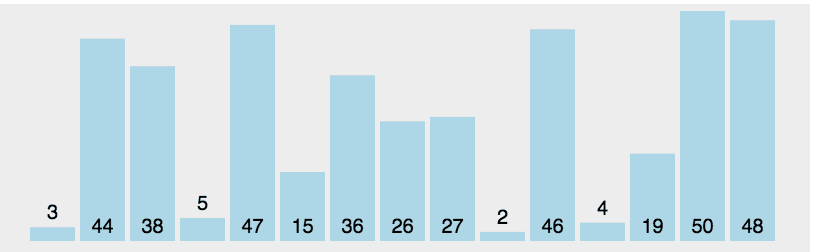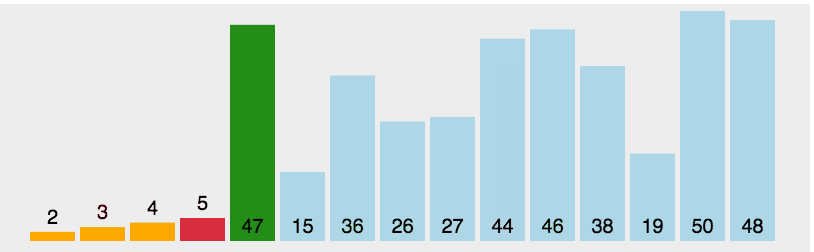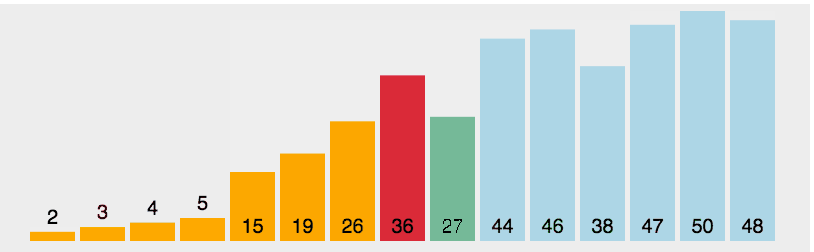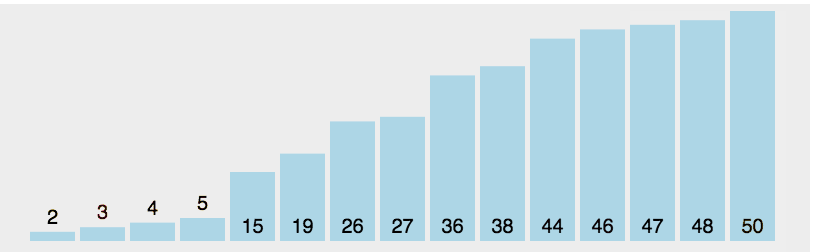
(2)图解
- 黄色:支点
- 绿色:比支点小的数据
- 紫色:比支点大的数据
- 红色:用来和支点比较大小的(现在比的位置)
- 橙色:已经比较好的数据
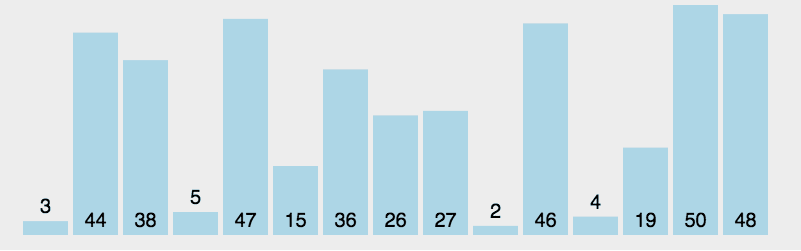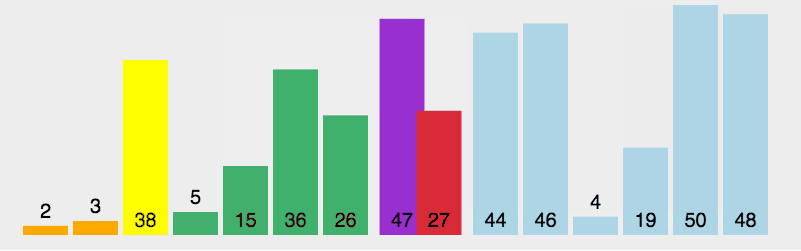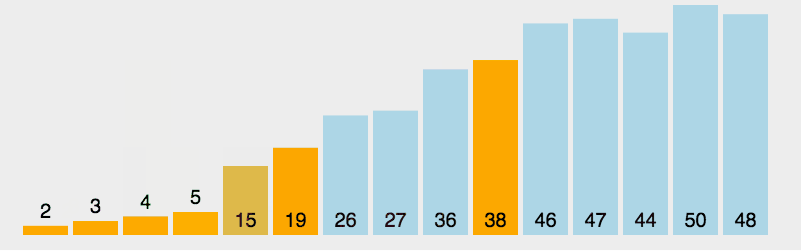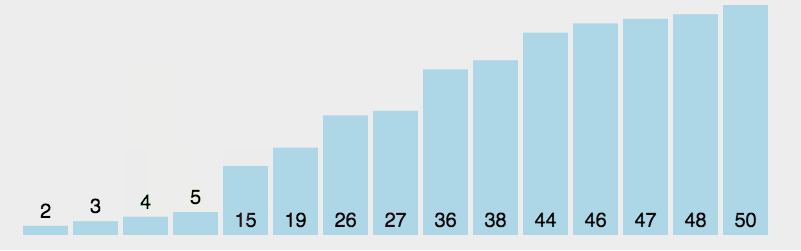
(3)示例代码
/********************************************************************************* @file quick_sort.c* @author feng* @version V0.0.1* @date 2025.09.26* @brief 快速排序的实现******************************************************************************** @attention** 本文档只供装逼学习使用,不得商用,违者必究** github: https://github.com/(求我拿链接)* CSDN: https://blog.csdn.net/(嘻嘻)* gitee: https://gitee.com/(求我拿链接)* 微信公众号: 测试中....* 有疑问或者建议:1740219515@qq.com** *******************************************************************************/#include <stdio.h>
#include <time.h>
#include <stdlib.h>/*** @brief 获取随机数,并返回* @note None* @param size: rand函数随机数范围的最大值* @retval 成功:返回获取到的随机数的值* 失败:返回-1*/
int QUICK_SORT_RandNum(int size)
{if (size > 32767){return -1;}return rand() % (size + 1);
}/*** @brief 显示数据* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval None*/
void QUICK_SORT_SHOW(int *data_p, int len)
{for (int i = 0; i < len; i++){printf("%d ", *(data_p + i));}printf("\n");
}/*** @brief 快速排序* @note None* @param data_p:指向要排序数据内存的指针* len:数据的内存长度* @retval 成功:返回0* 失败:返回-1*/
int QUICK_SORT(int *data_p, int len)
{if (len <= 1){return 0;}int i = 0;int j = len - 1;int temp = 0;while (i < j){while ((i < j) && (data_p[i] <= data_p[j])){j--;}if (i < j){temp = data_p[i];data_p[i] = data_p[j];data_p[j] = temp;}while ((i < j) && (data_p[i] <= data_p[j])){i++;}if (i < j){temp = data_p[i];data_p[i] = data_p[j];data_p[j] = temp;}}QUICK_SORT(data_p, i);QUICK_SORT(data_p + i + 1, len - i - 1);
}int main(int argc, char const *argv[])
{srand(time(NULL)); int test_data[128]={0};for (int i = 0; i < sizeof(test_data)/sizeof(test_data[0]); i++){test_data[i] = QUICK_SORT_RandNum(100);}printf("排序前:\n");QUICK_SORT_SHOW(test_data, sizeof(test_data) / sizeof(test_data[0]));printf("排序后:\n");QUICK_SORT(test_data, sizeof(test_data) / sizeof(test_data[0]));QUICK_SORT_SHOW(test_data, sizeof(test_data) / sizeof(test_data[0]));return 0;
}
5、希尔排序
(1)核心思路
希尔排序,以其发明者Donald Shell的名字命名,是插入排序的一种高效改进版本。它冲破了简单排序算法时间复杂度为O(n²)的屏障。其核心思想在于:让元素能够大跨度地移动,而不是像简单插入排序那样只能相邻移动,从而尽早地消除那些距离较远的逆序对,使序列宏观上快速接近有序。
普通的插入排序效率不高的一个原因是,它每次只能将元素移动一位。如果一个小元素位于序列的末端,则需要经过n-1次比较和移动才能到达正确位置,成本很高。
希尔排序的妙计是引入一个“增量序列”,通过分组插入排序来解决这个问题:
选择增量序列: 首先确定一个递减的增量序列,例如
..., 5, 3, 1。最后一个增量必须为1。增量决定了分组时元素之间的间隔。按增量分组并进行插入排序: 对于每个增量(例如Δ=5),将整个序列中所有相距为Δ的元素视为一组。然后分别对这些逻辑上的子序列进行插入排序。
减小增量,重复过程: 完成一轮排序后,减小增量(例如变为Δ=3),重复步骤2。随着增量的减小,每组包含的元素越来越多,序列也越来越有序。
最终进行一次标准的插入排序: 当增量减至1时,整个序列就是一组,进行最后一次标准的插入排序。由于此时序列已经“几乎有序”,这次插入排序的效率会非常高(接近O(n))。
简单来说: 希尔排序不是“一次成形”,而是通过“大步调”的预排序,使数据快速接近其最终位置,最后再用“小碎步”进行微调,从而大幅提高效率。
(2)图解
我们以序列 [84, 83, 88, 87, 61, 50, 70, 60, 80, 99] 进行升序排序为例:
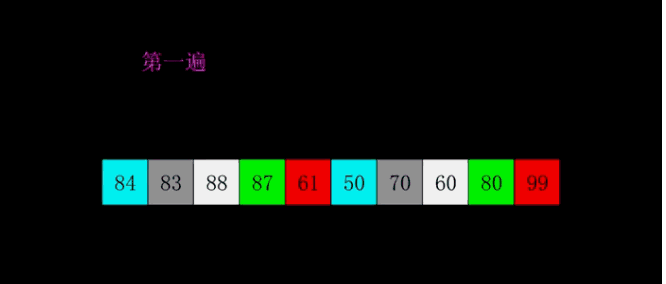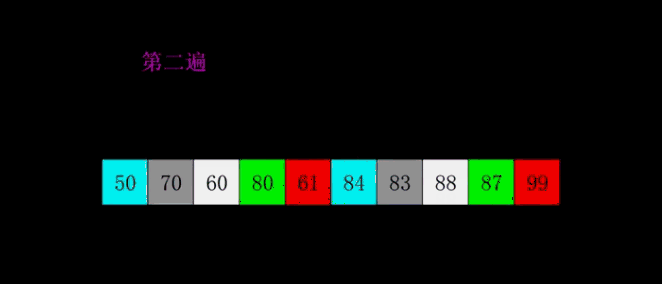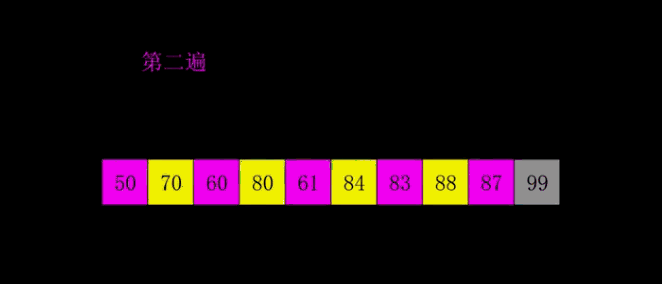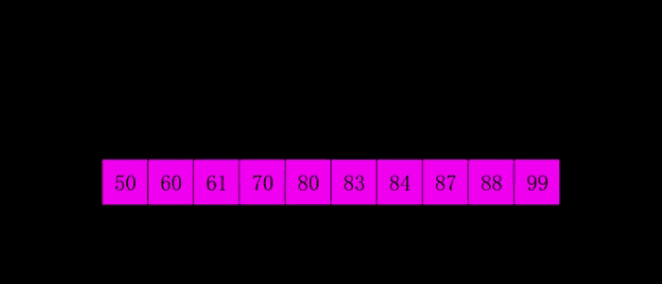
- 第一遍,先取间隔为(Δ=5Δ=5),即依次对以下5组数据进行排序:
- 第二遍,接下去缩小间隔重复如上过程。例如让间距Δ=3Δ=3:
- 第N遍,接下去继续不断减小间隔,最终令Δ=1Δ=1
(3)示例代码
/********************************************************************************* @file quick_sort.c* @author feng* @version V0.0.1* @date 2025.09.26* @brief 希尔排序的实现******************************************************************************** @attention** 本文档只供装逼学习使用,不得商用,违者必究** github: https://github.com/(求我拿链接)* CSDN: https://blog.csdn.net/(嘻嘻)* gitee: https://gitee.com/(求我拿链接)* 微信公众号: 测试中....* 有疑问或者建议:1740219515@qq.com** *******************************************************************************/#include <stdio.h>
#include <time.h>
#include <stdlib.h>/*** @brief 获取随机数,并返回* @note None* @param size: rand函数随机数范围的最大值* @retval 成功:返回获取到的随机数的值* 失败:返回-1*/
int SHELL_SORT_RandNum(int size)
{if (size > 32767){return -1;}return rand() % (size + 1);
}/*** @brief 显示数据* @note None* @param data_p:指向要显示数据内存的指针* len:数据的内存长度* @retval None*/
void SHELL_SORT_SHOW(int *data_p, int len)
{for (int i = 0; i < len; i++){printf("%d ", *(data_p + i));}printf("\n");
}/*** @brief 希尔排序* @note None* @param data_p:指向要排序数据内存的指针* len:数据的内存长度* delta:间隔排序数* @retval 成功:返回0* 失败:返回-1*/
int SHELL_SORT_DataSort(int *data_p, int len, int delta)
{if ((len <= 1) || (delta <= 0)){return -1;}int i=0;int j=0;int temp=0;for (i = delta; i < len*delta; i+=delta){temp = data_p[i];for (j = i-delta; j >= 0; j-=delta){if (temp < data_p[j]){data_p[j+delta] = data_p[j];}else{break;}}data_p[j+delta] = temp;}return 0;
}/*** @brief 希尔排序* @note None* @param data_p:指向要排序数据内存的指针* len:数据的内存长度* @retval 成功:返回0* 失败:返回-1*/int SHELL_SORT(int *data_p, int len){if ((data_p == NULL) || (len <= 1)){return -1;}for (int delta = len/2; delta > 0; delta/=2){for (int i = 0; i < delta; i++){SHELL_SORT_DataSort(data_p , len/delta, delta);}}}int main(int argc, char const *argv[]){srand(time(NULL)); int test_data[128]={0};for (int i = 0; i < sizeof(test_data)/sizeof(test_data[0]); i++){test_data[i] = SHELL_SORT_RandNum(100);}printf("排序前:\n");SHELL_SORT_SHOW(test_data, sizeof(test_data) / sizeof(test_data[0]));SHELL_SORT(test_data, sizeof(test_data) / sizeof(test_data[0]));printf("排序后:\n");SHELL_SORT_SHOW(test_data, sizeof(test_data) / sizeof(test_data[0]));return 0;}