未来做那些网站能致富一类电商平台都有哪些

前言

“数据驱动”的本质并非“堆砌数据”，而是让数据从“记录过去”的工具，转变为“指导未来”的决策依据。而实现这一转变的关键技术支点，正是以 “假设检验”为核心的统计推断体系。今天，我们将从技术运用到方法论心得，进行一场深度拆解。

---

第一章 数据驱动的基石：统计推断的技术框架全景

1.1 为什么假设检验是数据驱动的“钥匙”？

数据本身是沉默的，它不会直接告诉你“该做什么决策”。比如，新功能上线后日活有波动，这波动是“偶然”还是“必然”？此时，数据驱动的核心需求是：从杂乱现象中提炼可量化的“证据”，以此支持决策。

假设检验以“反证法”为逻辑核心：先对研究对象提出“初始假设”，再通过数据计算“若初始假设为真，观察到当前结果的概率”，最终判断“是否有足够证据推翻初始假设”。

业务场景示例

- 电商平台验证“个性化推荐是否提升点击率”：H0（原假设）为“个性化推荐与普通推荐点击率无差异”，H1（备择假设）为“个性化推荐点击率更高”。

- 医疗团队验证“新药是否降低并发症发生率”：H0为“新药与安慰剂并发症发生率无差异”，H1为“新药并发症发生率更低”。

假设检验将“业务问题”转化为“统计问题”，让数据以“概率”为语言，回答“要不要做某件事”。

1.2 思维导图的技术地图：从概念到工具的全局视角

假设检验技术体系：

-核心中枢：假设检验的核心逻辑（反证法、小概率事件原理）。

-基础概念分支：原假设、备择假设、检验统计量、显著性水平  α等，是理解检验的“语法规则”。

-置信区间分支：用“区间”描述“参数的可能范围”，是假设检验的“互补视角”（通过置信区间是否包含H0参数，可辅助决策）。

-检验方法分支：Z检验、t检验、卡方检验、方差分析等，是针对不同数据类型（连续/分类）、样本情况（大/小样本、单/多组）的“武器库”。

- p值与决策分支：p值的计算、解读，及结合α做决策的规则，是“从统计到业务”的关键环节。

-方法论延伸分支：非参数检验、多重比较、检验效力等，是解决复杂场景与实践陷阱的“进阶技巧”。

第二章 假设检验的技术实战：从原理到代码落地

2.1 基本概念拆解：原假设、备择假设与“反证法”逻辑

假设检验的逻辑是“反证法”：先假定H0为真，再观察“现实数据与H0的冲突程度”。

-原假设H0：通常是“无差异”“无效果”的假设（如“两组均值相等”“变量间无关联”），是我们要“挑战”的对象。

-备择假设H1：是真正想验证的“结论方向”（如“均值A > 均值B”“变量间有关联”），分单侧（方向明确，如“更高”“更低”）和双侧（方向不明，如“有差异”）。

为何这样设定？因为“证明存在”比“证明不存在”更简单。我们无法直接证明“个性化推荐有效”，但可通过“若无效，当前高点击率是小概率事件”，间接支持“有效”的结论。

案例：某APP更新登录界面，旧版本平均登录时长30秒。检验新版本是否“更快”：

-H0：μ= 30（新版本与旧版本时长无差异）。

-H1：μ< 30（新版本时长更短，单侧检验）。

2.2 检验统计量与分布：Z检验与t检验的“技术选择”

检验统计量是“衡量数据与H0差异程度”的量化指标，核心是“样本统计量与H0中参数的差异，除以统计量的标准误”（即“差异是标准误的多少倍”）。

2.2.1 Z检验：大样本或已知总体方差的场景

当总体方差σ2已知，或样本量 n ≥30 （中心极限定理，样本均值近似正态分布）时，用Z检验。统计量公式：Z=x-μ0σ/n 

其中，x为样本均值， μ0 为 H0中的总体均值， σ为总体标准差， n为样本量。

Python实战（Z检验）

某电商平台历史转化率15%（μ0=0.15），新策略下抽1000个用户（n=1000），转化率16.5%（x=0.165），已知总体标准差 σ=0.1。检验新策略是否提升转化率（单侧检验）。

```python

import numpy as np

from scipy import stats

mu0 = 0.15

x_bar = 0.165

sigma = 0.1

n = 1000

z_stat = (x_bar - mu0) / (sigma / np.sqrt(n))

p_value = 1 - stats.norm.cdf(z_stat)  # 单侧检验，取Z分布右侧面积

print(f"Z统计量：{z_stat:.4f}")

print(f"p值：{p_value:.6f}")

```

若p值 < 0.05（设 α=0.05），则拒绝H0，认为新策略有显著提升。

2.2.2 t检验：小样本且总体方差未知的场景

当样本量n < 30且总体方差未知时，用t检验（依赖t分布，自由度  df = n-1）。统计量公式：

t=x-μ0s/n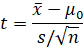

其中， s为样本标准差。

Python实战（单样本t检验）

某工厂零件标准长度5cm，随机抽10个零件，测量值：[4.8, 5.1, 4.9, 5.0, 5.2, 4.7, 4.9, 5.0, 5.1, 4.8]。检验是否符合标准（双侧检验，H0:μ=5；H1:μ≠5）。

```python

import numpy as np

from scipy.stats import ttest_1samp

sample = np.array([4.8, 5.1, 4.9, 5.0, 5.2, 4.7, 4.9, 5.0, 5.1, 4.8])

mu0 = 5.0

t_stat, p_value = ttest_1samp(sample, mu0)

print(f"t统计量：{t_stat:.4f}")

print(f"p值：{p_value:.4f}")

```

若p值 > 0.05，则不拒绝H0，认为零件长度符合标准。

2.3 置信区间：用“区间”描述“不确定性”的艺术

假设检验回答“是否有差异”，置信区间则回答“差异有多大，或参数在什么范围内”。定义：重复抽样时，若构造100个置信区间，约95个会包含真实总体参数（以95%置信水平为例）。

置信区间与假设检验的关系

若置信区间不包含H0中的参数，则拒绝H0；若包含，则不拒绝。例如，检验“μ=5”，若95%置信区间为(4.8, 4.9)，则拒绝μ=5的假设。

计算与可视化（Z检验的置信区间）

公式： x±Zα/2×σn（双侧95%置信水平时，Zα/2=1.96）。

Python实战

用前文电商转化率案例，计算95%置信区间并可视化。

```python

import numpy as np

import matplotlib.pyplot as plt

x_bar = 0.165

sigma = 0.1

n = 1000

z_critical = 1.96  # 95%置信水平

margin_error = z_critical * (sigma / np.sqrt(n))

ci_lower = x_bar - margin_error

ci_upper = x_bar + margin_error

print(f"95%置信区间：({ci_lower:.4f}, {ci_upper:.4f})")

# 可视化误差棒图

plt.errorbar(x=0, y=x_bar, yerr=margin_error, fmt='o', capsize=5)

plt.axhline(y=0.15, color='r', linestyle='--', label='原转化率')

plt.legend()

plt.title('新策略转化率的95%置信区间')

plt.ylabel('转化率')

plt.show()

```

若红色虚线（原转化率0.15）不在误差棒区间内，说明新策略与原策略有显著差异。

2.4 卡方检验：分类数据的“关联与分布”检验

当数据是分类变量（如性别：男/女；用户等级：青铜/白银/黄金）时，用卡方检验，分为“卡方拟合优度检验”（检验分类数据是否符合某一分布）和“卡方独立性检验”（检验两个分类变量是否有关联）。

卡方独立性检验：原理与实战

核心公式（Pearson卡方统计量）：

χ2=i,jOij-Eij2Eij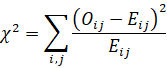

其中，Oij 为观察频数，Eij为“变量独立时的期望频数”。

业务案例：检验“用户性别”与“购买品类（电子产品/服装/家居）”是否有关联，数据如下：

|          | 电子产品 | 服装 | 家居 | 合计 |

|----------|----------|------|------|------|

| 男       | 40       | 25   | 15   | 80   |

| 女       | 20       | 30   | 30   | 80   |

| 合计     | 60       | 55   | 45   | 160  |

Python实战

```python

from scipy.stats import chi2_contingency

import numpy as np

contingency_table = np.array([

    [40, 25, 15],

    [20, 30, 30]

])

chi2, p_value, df, expected = chi2_contingency(contingency_table)

print(f"卡方统计量：{chi2:.4f}")

print(f"p值：{p_value:.4f}")

print(f"自由度：{df}")

print("期望频数：")

print(expected)

```

若p值 < 0.05，则拒绝“性别与购买品类独立”的原假设，认为两者有关联。

第三章 p值：数据驱动决策的“量化标尺”

3.1 p值的本质：“证据强度”的数值表达

p值定义：在原假设H0为真的前提下，观察到当前样本结果（或更极端结果）的概率。

常见误解澄清

- p值不是“原假设为真的概率”（原假设是“假定为真”，而非“有多少概率为真”）。

- p值小，说明“若H0为真，当前数据是小概率事件”，因此有理由怀疑H0。

案例：抛硬币检验是否公平（H0:p=0.5，H1:p≠0.5)。抛10次，出现9次正面。计算p值：“更极端的结果”包括“9次正面、10次正面、1次正面、0次正面”。用二项分布计算概率：

PX≥9 或 X≤1=PX=9+PX=10+PX=0+PX=1

计算得p值约0.021 < 0.05，因此拒绝“硬币公平”的假设。

3.2 p值与显著性水平α：决策的“边界”在哪里？

显著性水平α是预先设定的“小概率阈值”（常用0.05、0.01、0.1），代表“允许的误判风险”（第一类错误：H0为真却被拒绝的概率）。

- 若p ≤α：拒绝H0，认为“有显著证据支持H1”。

- 若p > α：不拒绝H0，认为“证据不足，无法推翻H0”。

α的选择逻辑

- 业务风险高（如医疗、金融）：选更小的α（如0.01），降低“假阳性”风险。

- 业务需快速迭代（如互联网A/B测试）：可接受稍大的α（如0.05甚至0.1），平衡“决策效率”与“风险”。

3.3 从p值到业务行动：A/B测试的“决策链”案例

场景：某互联网公司测试两个APP首页版本（A版：原版本；B版：新设计版），核心指标“用户停留时长”。

1. 设定假设

H0：μA=μB（两版本停留时长无差异）；

    H1：μB>μA（B版停留时长更长，单侧检验）。

2.数据收集

    随机分配1000名用户到A组，1000名到B组，收集24小时内停留时长数据。

3.统计检验

    用双样本t检验（假设方差未知），得统计量t=2.35，p值=0.0096（α=0.05）。

4.决策与行动

    因p值 < 0.05，拒绝H0，认为B版显著提升停留时长。产品团队全量上线B版，并基于此提出新假设“B版的某一模块（如推荐流）是提升关键”，进入下一轮测试。

第四章 高级技术拓展：从“单维度”到“多维度”推断

4.1 双样本检验与方差分析：“多组数据”的比较艺术

4.1.1 双样本t检验：两组数据的差异检验

需比较“两组独立样本”（如“新用户”与“老用户”购买频次）或“配对样本”（如“同一用户使用功能前后的满意度”）时，用双样本t检验。

    -独立双样本t检验：假设两组方差相等或不等（通过方差齐性检验判断），统计量基于两组均值差。

-配对t检验：关注“差值的均值是否为0”，能有效控制个体差异（如同一用户的前后对比）。

Python实战（独立双样本t检验）

```python

from scipy.stats import ttest_ind

np.random.seed(42)

a_group = np.random.normal(5.2, 1.5, 500)  # 老用户平均5.2次

b_group = np.random.normal(4.8, 1.2, 500)  # 新用户平均4.8次

t_stat, p_value = ttest_ind(a_group, b_group, equal_var=False)  # 不假设方差相等

print(f"t统计量：{t_stat:.4f}")

print(f"p值：{p_value:.4f}")

```

若p值 < 0.05，认为两组购买频次有显著差异。

4.1.2 方差分析（ANOVA）：多组数据的“同时比较”

需比较三组及以上数据（如“青铜、白银、黄金会员的消费额”）时，若用多次双样本t检验，会增加“假阳性”概率（多重比较问题）。此时用方差分析，通过“分解方差”判断“组间差异是否大于组内差异”。

核心逻辑：若“组间方差”远大于“组内方差”，则认为组间存在显著差异。

Python实战（单因素方差分析）

```python

import statsmodels.api as sm

from statsmodels.formula.api import ols

import pandas as pd

import numpy as np

# 模拟三组会员消费额数据

np.random.seed(42)

bronze = np.random.normal(100, 20, 200)

silver = np.random.normal(150, 25, 200)

gold = np.random.normal(220, 30, 200)

# 合并数据为DataFrame

data = pd.DataFrame({

    'consumption': np.concatenate([bronze, silver, gold]),

    'member_level': ['bronze']*200 + ['silver']*200 + ['gold']*200

})

# 拟合方差分析模型

model = ols('consumption ~ C(member_level)', data=data).fit()

anova_table = sm.stats.anova_lm(model, typ=2)

print(anova_table)

```

若“PR(>F)”（p值） < 0.05，说明不同会员等级的消费额存在显著差异。

4.2 非参数检验：突破“分布假设”的限制

参数检验（如t检验、Z检验）依赖“数据服从特定分布”的假设（如正态分布）。当数据不满足正态分布（如小样本、严重偏态、存在异常值）时，需用非参数检验（不依赖分布假设）。

常见非参数检验方法

-单样本/配对样本：Wilcoxon符号秩检验（替代配对t检验）。

-独立样本：Mann-Whitney U检验（替代独立双样本t检验）。

-多组样本：Kruskal-Wallis检验（替代方差分析）。

案例与实战

某小样本数据（n=12）严重右偏，需检验“中位数是否大于20”。用Wilcoxon符号秩检验：

```python

from scipy.stats import wilcoxon

np.random.seed(42)

sample = np.random.exponential(scale=30, size=12) + 10  # 偏态分布，中位数约25

diff = sample - 20

stat, p_value = wilcoxon(diff, alternative='greater')

print(f"Wilcoxon统计量：{stat}")

print(f"p值：{p_value:.4f}")

```

若p值 < 0.05，认为中位数显著大于20。

第五章 数据驱动的方法论心得：从“技术”到“思维”的升华

掌握技术只是第一步，更重要的是把统计推断的逻辑内化为“数据驱动的思维方式”。以下是实战中沉淀的方法论心得。

5.1 技术不是目的，“对齐业务目标”才是

假设检验是工具，而非“为了检验而检验”。每次开展统计推断前，必须明确：

-业务问题是什么？ （如“新功能是否提升付费率？”）

-假设如何从业务问题中提炼？（\( H_0 \)：“付费率无变化”；\( H_1 \)：“付费率提升”）

-统计结果如何指导业务行动？（若p<0.05，全量上线；否则，优化后再测）

反例警示：曾有团队为“做出显著结果”，反复调整样本、修改假设，最终得到“p<0.05”，但业务上线后数据暴跌——因脱离“提升付费率”的核心目标，陷入“p值陷阱”。

5.2 拥抱“不确定性”：统计思维的核心

数据驱动不是追求“绝对正确”，而是量化不确定性，并在不确定性下做“最优决策”。

- 用“置信区间”替代“点估计”：不说“新策略提升2%点击率”，而说“在95%置信水平下，点击率提升1.2%-3.5%”——既传达“提升”结论，又明确“提升幅度的波动范围”。

- 向业务方“翻译”统计结果：避免“p<0.05”等技术术语，改用“有95%的把握，新策略能提升点击率”。

5.3 迭代与验证：数据驱动的“闭环思维”

一次假设检验不是终点，而是“数据驱动闭环”的起点： 提出假设→检验→解读结果→提炼新假设→再检验 。

案例

- 第一次检验：“个性化推荐 vs 普通推荐，点击率是否有差异？” → 结论：有差异。

- 第二次检验：“个性化推荐的‘算法A’ vs ‘算法B’，哪种点击率更高？” → 结论：算法A更好。

- 第三次检验：“算法A在‘早高峰’ vs ‘晚高峰’推送，哪个时段效果更好？” → 持续优化...

通过“小步快跑，快速迭代”，让数据驱动从“单次决策”变成“持续优化”。

5.4 规避统计陷阱：实战中的“避坑指南”

陷阱1：p-hacking（为显著结果而“折腾”数据）

表现：反复调整样本（如只选“活跃用户”）、修改假设（从双侧改单侧）、多次检验后挑p值最小的结果。

应对：预先注册分析计划（明确样本、假设、方法），或用“多重比较校正”（如Bonferroni校正）。

陷阱2：忽视样本量与“检验效力”

表现：样本量太小，可能导致“第二类错误”（H0为假却未被拒绝，即“漏检真实效果”）。

应对：提前做“检验效力分析”，计算所需最小样本量（如用`statsmodels`的`power.tt_ind_solve_power`）。

陷阱3：“显著”≠“重要”

表现：统计显著（p<0.05）不代表业务重要。如，新策略使点击率提升0.1%（p=0.04），但投入产出比极低，此时“显著”无业务价值。

应对：同时关注“效应量”（如 Cohen's d、R²），结合业务ROI判断。

第六章 实战案例全景：从“电商”到“医疗”的 data-driven 故事

6.1 电商场景：推荐算法的“效果闭环”

背景：电商平台优化“首页推荐算法”，目标提升“用户点击推荐商品的概率”。

步骤1：提出假设

H0：“新算法与旧算法的点击概率无差异”；

H1：“新算法点击概率更高”（单侧检验）。

步骤2：实验设计

- 流量分割：1%用户随机分两组，A组（旧算法，n=5000），B组（新算法，n=5000）。

- 指标定义：“推荐商品的点击率”（点击数/推荐曝光数）。

步骤3：数据收集与检验

- 旧算法点击率：3.2%；新算法点击率：3.8%。

- 用Z检验（大样本，单侧），得p值=0.002 < 0.05，拒绝 H0。

步骤4：业务行动与迭代

- 结论：新算法显著提升点击率，全量上线。

- 迭代：基于新算法数据，发现“女性用户点击率提升更明显”，提出新假设“针对女性用户的推荐策略是否更优？”，进入下一轮测试。

6.2 医疗场景：新药疗效的“严谨验证”

背景：药企研发新药，验证“是否能降低高血压患者的收缩压”。

步骤1：提出假设

H0：“新药与安慰剂的收缩压降低值无差异”；

H1：“新药降低值更大”（单侧检验）。

步骤2：实验设计（RCT）

- 随机双盲：200名患者随机分两组，每组100人，A组服新药，B组服安慰剂。

- 指标：服药8周后，收缩压的“降低值”（基线值 - 8周后值）。

步骤3：数据收集与检验

- 新药组平均降低值：15.2mmHg，标准差4.3；安慰剂组平均降低值：8.7mmHg，标准差3.9。

- 用双样本t检验（独立样本，方差齐性），得t=10.2，p<0.001，拒绝 \( H_0 \)。

步骤4：临床与统计的“交叉解读”

- 统计结论：新药显著降低收缩压。

- 临床结论：降低15.2mmHg具有临床意义（高血压治疗中，5mmHg的降低就有健康获益），因此新药可进入下一阶段试验。

6.3 制造业场景：产品质量的“过程控制”

背景：汽车零部件厂监控“零件直径”是否符合标准（50±0.5mm）。

步骤1：实时检验假设

每次抽样n=10个零件，检验H0：“直径均值=50mm”； H1：“直径均值≠50mm”。

步骤2：统计过程与行动

- 若某批次t检验p<0.05：拒绝H0，启动“过程调查”（如检查机床、原材料）。

- 同时，计算95%置信区间：若区间包含50但接近边界（如49.9-50.1），则提前调整工艺，预防“即将不合格”。

价值：从“事后检验次品”升级为“事前预防偏差”，用数据驱动实现“质量的持续稳定”。

第七章 工具链与生态：让数据驱动“更高效”

7.1 Python生态：从“scipy”到“statsmodels”的利器

- `scipy.stats`：基础统计检验（t检验、卡方检验、非参数检验等）的“瑞士军刀”。

- `statsmodels`：更复杂的统计模型（方差分析、线性回归、时间序列等），输出更详细的统计结果（如ANOVA表、回归系数的置信区间）。

- `pandas`：数据预处理（分组、聚合、缺失值处理），为检验提供“干净的数据”。

- `matplotlib/seaborn`：结果可视化（箱线图、误差棒图、森林图等），让统计结论“一目了然”。

7.2 可视化辅助：让“统计结果”更易理解

- 箱线图+散点图：展示多组数据的分布与差异，直观判断“是否有异常值”。

- 森林图：展示多组置信区间，对比“不同分组的效应范围”。

- 功率曲线：展示“样本量-检验效力”的关系，辅助实验设计。

Python实战（森林图绘制）

```python

import matplotlib.pyplot as plt

import numpy as np

# 模拟多组置信区间数据

groups = ['A', 'B', 'C', 'D']

means = [2.5, 3.2, 1.8, 4.0]

std_errors = [0.3, 0.4, 0.25, 0.5]

ci_lower = [m - 1.96*se for m, se in zip(means, std_errors)]

ci_upper = [m + 1.96*se for m, se in zip(means, std_errors)]

# 绘制森林图

plt.figure(figsize=(8, 6))

plt.errorbar(means, range(len(groups)), xerr=[[m - l for m, l in zip(means, ci_lower)],

                                              [u - m for m, u in zip(means, ci_upper)]],

             fmt='o', capsize=5, color='black')

plt.axvline(x=0, color='r', linestyle='--')  # 参考线（如H0中的参数）

plt.yticks(range(len(groups)), groups)

plt.xlabel('效应值（及95%置信区间）')

plt.title('多组效应的森林图')

plt.show()

```

7.3 自动化与 Pipeline：“大规模场景”的效率提升

当需处理成百上千次检验（如“全链路指标监控”“多变量A/B测试”）时，手动逐个检验效率极低。此时需构建**自动化的统计检验Pipeline：

1.数据层：从数仓/数据库批量读取待检验的数据集。

2.假设生成层：根据业务规则自动生成假设（如“每个页面的转化率是否高于基准值”）。

3.检验执行层：用循环/并行计算，对每个假设自动执行检验（t检验、卡方检验等）。

4.结果汇总层：将p值、置信区间、效应量等结果汇总成报表。

5.可视化层：自动生成Dashboard，高亮“显著结果”。

代码框架示例（简化版）

```python

import pandas as pd

from scipy.stats import ttest_1samp

import numpy as np

# 1. 读取多组数据（示例：多个页面的转化率）

data = pd.read_excel("multiple_pages_data.xlsx")

pages = data['page_id'].unique()

# 2. 基准值（整体平均转化率）

baseline = data['conversion_rate'].mean()

# 3. 批量检验

results = []

for page in pages:

    page_data = data[data['page_id'] == page]['conversion_rate']

    t_stat, p_value = ttest_1samp(page_data, baseline)

    ci_lower = page_data.mean() - 1.96 * (page_data.std() / np.sqrt(len(page_data)))

    ci_upper = page_data.mean() + 1.96 * (page_data.std() / np.sqrt(len(page_data)))

    results.append({

        'page_id': page,

        'mean_conv': page_data.mean(),

        't_stat': t_stat,

        'p_value': p_value,

        'ci_lower': ci_lower,

        'ci_upper': ci_upper

    })

# 4. 结果汇总与输出

results_df = pd.DataFrame(results)

results_df['is_significant'] = results_df['p_value'] < 0.05

results_df.to_csv("page_conversion_tests.csv", index=False)

```

---

结语：数据驱动的未来，统计推断的“永恒价值”

在AI大模型、大数据技术层出不穷的今天，有人会问：“假设检验这些‘传统统计方法’，还重要吗？”

答案是：更重要了。

因为数据驱动的本质，是“用理性代替直觉，用证据指导决策”。而统计推断，正是“量化证据、管理不确定性”的核心逻辑。大模型能生成“看似合理”的结论，但假设检验能告诉你“这个结论在统计上是否可靠”；大数据能提供“海量信息”，但统计推断能帮你“提炼出决策所需的关键证据”。

掌握假设检验的技术，更要内化其背后的“数据驱动思维”——技术是工具，业务是目的；不确定性是常态，量化与迭代是应对之道。唯有如此，才能让数据真正成为“驱动业务增长、创造价值”的引擎，而不是躺在数据库里的冰冷数字。

希望这篇从技术到方法的深度拆解，能让你在“数据驱动”的道路上，走得更扎实、更清醒。