振动力学|01 单自由度系统的振动分析
振动力学|01 单自由度系统的振动分析
⭐ 🌟 💫
文章目录
- 振动力学|01 单自由度系统的振动分析
- 单自由度系统的自由振动
- 无粘性阻尼的自振动
- 有粘性阻尼的自由振动
- 单自由度系统的简谐强迫振动
- 简谐激励力下的强迫振动
- 旋转不平衡质量引起的强迫振动
- 基础运动引起的强迫振动
- 非简谐激励强迫振动
- 周期激励下的强迫振动
- 一般激励下的系统响应
- 一般激励力下的系统响应
- 一般基础运动激励下的系统响应
单自由度系统的自由振动
最典型的单自由度系统的自由振动是弹簧质量系统。
无粘性阻尼的自振动
对于不计阻尼的单自由度系统,仅有刚度kkk的无质弹簧与质点只可沿弹簧轴线方向运动,以平衡位置为坐标原点的运动微分方程:
x¨+ωn2x=0\ddot{x}+\omega_n^2x=0x¨+ωn2x=0
其中,ωn=km=gλs\omega_{n}=\sqrt{\dfrac {k}{m}}=\sqrt{\dfrac{g}{\lambda_s}}ωn=mk=λsg。
定理:任意时刻初始信息推导全局运动方程。
设t=τt=\taut=τ时刻的初始位移和初始速度:xτx_{\tau}xτ与x˙τ\dot{x}_{\tau}x˙τ。有:
x(t)=xτcos(ωn(t−τ))+x˙τωnsin(ωn(t−τ))x(t)=x_{\tau}\cos{(\omega_{n}(t-\tau))}+\frac{\dot{x}_{\tau}}{\omega_n}\sin{(\omega_n(t-\tau))}x(t)=xτcos(ωn(t−τ))+ωnx˙τsin(ωn(t−τ))
除了通过矢量力学的方法,还可以通过能量方法求得系统的运动微分方程,设系统任意一个时刻的动能为TTT以及势能UUU,由机械能守恒:
d(T+U)dt=0\frac{\mathrm{d}(T+U)}{\mathrm{dt}}=0dtd(T+U)=0
由于实际工程问题中,弹性元件的质量不可忽略,因此需要在一定的振动时的形状假设下,进行更精确的计算。设质量为mmm的单位位移时弹簧距离非自由端sss处的位移f(s)f(s)f(s),那么在该点处的位移函数:
η(s,t)=x(t)f(s),0≤s≤l\eta(s,t)=x(t)f(s),\quad 0 \leq s \leq lη(s,t)=x(t)f(s),0≤s≤l
因此,相关的物理量计算如下。
首先,弹簧上一点的速度计算为:
η˙(s,t)=x˙(t)f(s)\dot{\eta}(s,t)=\dot{x}(t)f(s)η˙(s,t)=x˙(t)f(s)
其次,弹簧整体的动能:
Tk=∫0l12ρη˙2(s,t)ds=12ρx˙2∫0lf2(s)ds\begin{align*}T_k&=\int_{0}^{l}\frac{1}{2}\rho \dot{\eta}^2(s,t)\mathrm{d}s\\ &=\frac{1}{2}\rho \dot{x}^2\int_0^{l}f^2(s)\mathrm{d}s \end{align*} Tk=∫0l21ρη˙2(s,t)ds=21ρx˙2∫0lf2(s)ds
记弹簧等效质量:me=∫0lf2(s)dsm_e=\int_{0}^{l}f^{2}(s)\mathrm{d}sme=∫0lf2(s)ds
有粘性阻尼的自由振动
最常用的一种阻尼模型是粘性阻尼,或者称粘滞阻尼,其特性为与相对速度大小成正比,即:
Pd=cvP_d=cvPd=cv
其中,PdP_dPd是粘性阻尼力,vvv是相对速度,ccc是阻尼系数。
这里详细介绍一下粘性阻尼的生成机制
如图展示了一个直径为DDD长度为LLL的活塞,带有nnn和直径为ddd的小孔。油的黏度为μ\muμ,密度为ρ\rhoρ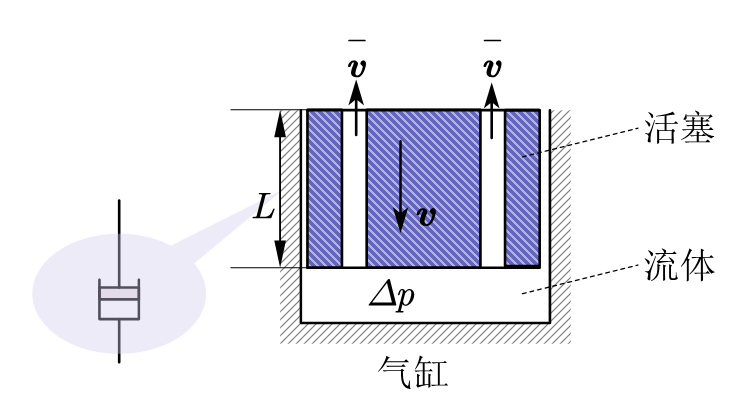
由Hagen - Poiseuille 公式:
Δp=32Lμv‾d2\Delta p=\frac{32L\mu\overline{v}}{d^2}Δp=d232Lμv
由流体的连续性假设:
v‾=1n(Dd)2v\overline{v}=\frac{1}{n}\left(\frac{D}{d}\right)^2vv=n1(dD)2v
将v‾=1n(Dd)2v\overline{v}=\frac{1}{n}\left(\frac{D}{d}\right)^2vv=n1(dD)2v代入Hagen - Poiseuille 公式:
Δp=32LμnD2(Dd)4v\Delta p=\frac{32 L\mu}{nD^2}\left(\frac{D}{d}\right)^4vΔp=nD232Lμ(dD)4v
对活塞受力分析忽略活塞重力并由压强的定义,知道作用于活塞上的阻力FdF_dFd:
Δp=Fdπ4d2\Delta p=\frac{F_d}{\frac{\pi}{4}d^2}Δp=4πd2Fd
代入即可得到:
Fd=4πLμ(Dd)4vF_d=4\pi L \mu \left(\frac{D}{d}\right)^4vFd=4πLμ(dD)4v
加上方向有:
Fd=−4πLμ(Dd)4v\boldsymbol{F}_d=-4\pi L \mu \left(\frac{D}{d}\right)^4\boldsymbol{v}Fd=−4πLμ(dD)4v
对于粘性阻尼的自由振动,我们可以得到如下运动微分方程:
mx¨+cx˙+kx=0m\ddot{x}+c\dot{x}+kx=0mx¨+cx˙+kx=0
记:
{ξ≜c2mωnωn≜km\begin{cases} \xi \triangleq \frac{c}{2m\omega_n}\\ \omega_n \triangleq \sqrt{\frac{k}{m}} \end{cases} {ξ≜2mωncωn≜mk
上述动力学方程转化为:
x¨+2ξωnx+ωn2x=0\ddot{x}+2\xi \omega_n{x}+\omega_n^2x=0x¨+2ξωnx+ωn2x=0
接下来需要对这个微分方程进行分析,这里介绍两种不同的角度:
角度一:从特征方程方法确定解的性质
这一部分要求熟悉高数的二阶常系数线性齐次微分方程求解方法。
关于这一部分可以去我的“分析与几何专栏下的ODE查看”。这里做简要的介绍:
| 特征方程根 r2+pr+q=0r^2 + pr + q = 0r2+pr+q=0 的情况 | 微分方程 y′′+py′+qy=0y'' + py' + qy = 0y′′+py′+qy=0 通解公式 |
|---|---|
| 相异实根 r1≠r2r_1 \neq r_2r1=r2 | y=C1er1x+C2er2xy = C_1 e^{r_1 x} + C_2 e^{r_2 x}y=C1er1x+C2er2x |
| 相等实根 r1=r2r_1 = r_2r1=r2 | y=(C1+C2x)er1xy = (C_1 + C_2 x) e^{r_1 x}y=(C1+C2x)er1x |
| 一对共轭复根 r1,2=α±iβr_{1,2} = \alpha \pm i\betar1,2=α±iβ | y=eαx(C1cosβx+C2sinβx)y = e^{\alpha x}(C_1 \cos\beta x + C_2 \sin\beta x)y=eαx(C1cosβx+C2sinβx) |
有阻尼情况下的振动方程的特征方程为:
r2+2ξωnr+ωn2=0r^2+2\xi \omega_n r+\omega_n^2 =0r2+2ξωnr+ωn2=0
特征值为:
r1,2=(−ξ±ξ2−1)ωnr_{1,2}=\left(-\xi \pm \sqrt{\xi^2-1}\right)\omega_nr1,2=(−ξ±ξ2−1)ωn
如图对不同的阻尼比进行讨论,可以得到不同形式的初解:
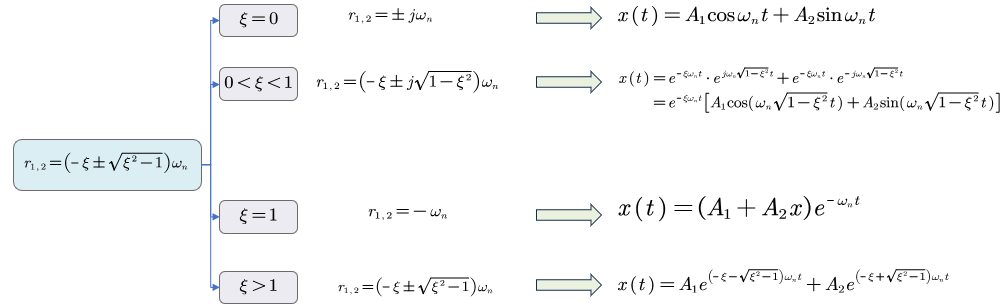
- 当ξ=0\xi =0ξ=0,时:
r1,2=±jωnr_{1,2}=\pm j\omega _nr1,2=±jωn
此时的解为:
x(t)=C1ejωnt+C2e−jωnt=eiθ=cosθ+isinθA1cosωnt+A2sinωntx(t)=C_1e^{j\omega _n t}+C_2e^{-j\omega _n t}\stackrel{e^{i\theta}=\cos{\theta}+i\sin{\theta}}{=}A_1\cos{\omega _n}t + A_2\sin{\omega _n}t x(t)=C1ejωnt+C2e−jωnt=eiθ=cosθ+isinθA1cosωnt+A2sinωnt
其中,C1,C2∈CC_1,C_2\in \mathbb{C}C1,C2∈C,A1,A2∈RA_1,A_2\in \mathbb{R}A1,A2∈R。
- 当 ξ∈[0,1)\xi \in [0,1)ξ∈[0,1)
r1,2=(−ξ±j1−ξ2)ωnr_{1,2}=\left( -\xi \pm j\sqrt{1-\xi ^2} \right) \omega _nr1,2=(−ξ±j1−ξ2)ωn
此时的解为:
x(t)=e−ξωnt⋅ejωn1−ξ2t+e−ξωnt⋅e−jωn1−ξ2t=e−ξωnt[A1cos(ωn1−ξ2t)+A2sin(ωn1−ξ2t)]\begin{align*} x(t) &= e^{-\xi\omega_n t} \cdot e^{j\omega_n\sqrt{1-\xi^2} t} +e^{-\xi\omega_n t} \cdot e^{-j\omega_n\sqrt{1-\xi^2} t} \\ &=e^{-\xi\omega_n t} \left[ A_1\cos( \omega_n\sqrt{1-\xi^2} t) + A_2\sin( \omega_n\sqrt{1-\xi^2} t) \right] \end{align*}x(t)=e−ξωnt⋅ejωn1−ξ2t+e−ξωnt⋅e−jωn1−ξ2t=e−ξωnt[A1cos(ωn1−ξ2t)+A2sin(ωn1−ξ2t)]
- ξ=1\xi =1ξ=1时,
r1,2=−ωnr_{1,2}=-\omega _nr1,2=−ωn
此时的解为:
x(t)=(A1+A2x)e−ωntx(t)=\left(A_1+A_2x\right)e^{-\omega _n t }x(t)=(A1+A2x)e−ωnt
- 当 ξ>1\xi > 1ξ>1时,
r1,2=(−ξ±ξ2−1)ωnr_{1,2}=\left( -\xi \pm \sqrt{\xi ^2-1} \right) \omega _nr1,2=(−ξ±ξ2−1)ωn
此时的解为:
x(t)=A1e(−ξ−ξ2−1)ωnt+A2e(−ξ+ξ2−1)ωntx(t)=A_1e^{\left( -\xi - \sqrt{\xi ^2-1} \right) \omega _n t}+A_2e^{\left( -\xi + \sqrt{\xi ^2-1} \right) \omega _n t}x(t)=A1e(−ξ−ξ2−1)ωnt+A2e(−ξ+ξ2−1)ωnt
角度二:使用L\mathscr{L}L变换
以后说。
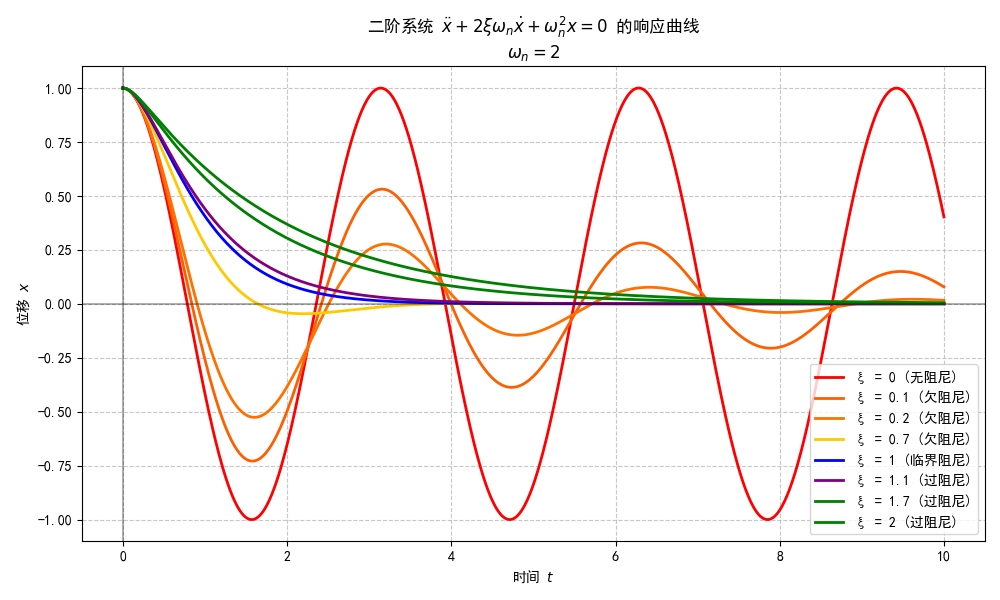
对以上不同阻尼比下的动力学方程进行仿真如图所示:
单自由度系统的简谐强迫振动
简谐激励力下的强迫振动
对于单自由度的系统而言,现考虑其受到正弦激励P0sinωtP_0\sin{\omega t}P0sinωt,由矢量力学得:
mx¨+cx˙+kx=P0sinωtm\ddot{x}+c\dot{x}+kx=P_0\sin{\omega t}mx¨+cx˙+kx=P0sinωt
记相对阻尼系数为ζ\zetaζ,ζ=nωn=c2mωn\zeta = \dfrac {n}{\omega_n}=\dfrac{c}{2m\omega_n}ζ=ωnn=2mωnc,将公式mx¨+cx˙+kx=P0sinωtm\ddot{x}+c\dot{x}+kx=P_0\sin{\omega t}mx¨+cx˙+kx=P0sinωt转化:
x¨+2ζωnx˙+ωn2x=P0sinωtm\ddot{x}+2\zeta \omega_n\dot{x}+\omega_n^2x=\frac{P_0\sin{\omega t}}{m}x¨+2ζωnx˙+ωn2x=mP0sinωt
延拓复数域后,原方程转化为:
X¨+2ζωnX˙+ωn2X=P0ejωtm\ddot{X}+2\zeta \omega_n\dot{X}+\omega_n^2X=\frac{P_0e^{j\omega t}}{m}X¨+2ζωnX˙+ωn2X=mP0ejωt
设特解的形式为:
X~(t)=X~ejωt\widetilde{X}(t)=\widetilde{X}e^{j\omega t}X(t)=Xejωt
其中,X~\widetilde{X}X为复振幅。
可以求得:
X~(t)=P0mejωtωn2−ω2+j2ζωnω\widetilde{X}(t)=\frac{P_0}{m}\frac{e^{j\omega t}}{\omega_n^2-\omega^2+j2\zeta\omega_n\omega}X(t)=mP0ωn2−ω2+j2ζωnωejωt
化简后为:
X~(t)=P0m(ωn2−ω2)2+(2ζωnω)2ej(ωt−arctan2ζωnωωn2−ω2)\widetilde{X}(t)=\frac{P_0}{m\sqrt{\left(\omega_n^2-\omega^2\right)^2+\left(2\zeta \omega_n \omega\right)^2}}e^{j\left(\omega t-\arctan\frac{2\zeta \omega_n \omega}{\omega_n^2-\omega^2}\right)}X(t)=m(ωn2−ω2)2+(2ζωnω)2P0ej(ωt−arctanωn2−ω22ζωnω)
若记频率比r=ωωnr=\dfrac{\omega}{\omega_n}r=ωnω,特解可化简为:
X~(t)=P0k(1−r2)2+(2ζr)2ej(ωt−arctan2ζr1−r2)\widetilde{X}(t)=\frac{\frac{P_0}{k}}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}e^{j\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right)}X(t)=(1−r2)2+(2ζr)2kP0ej(ωt−arctan1−r22ζr)
由于力是取虚部,因此实际位移为虚部,得到实特解:
x~(t)=Im[P0k(1−r2)2+(2ζr)2ej(ωt−arctan2ζr1−r2)]=P0k(1−r2)2+(2ζr)2sin(ωt−arctan2ζr1−r2)\begin{align*} \widetilde{x}(t)&=\text{Im}\left[\frac{\frac{P_0}{k}}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}e^{j\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right)}\right]\\ &=\frac{\frac{P_0}{k}}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}\sin\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right) \end{align*}x(t)=Im[(1−r2)2+(2ζr)2kP0ej(ωt−arctan1−r22ζr)]=(1−r2)2+(2ζr)2kP0sin(ωt−arctan1−r22ζr)
我们称MMM为振幅放大因子:
M=1(1−r2)2+(2ζr)2M=\frac{1}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}M=(1−r2)2+(2ζr)21
我们对放大因子MMM与阻尼比ζ\zetaζ和频率比rrr之间进行如图所示数值仿真:
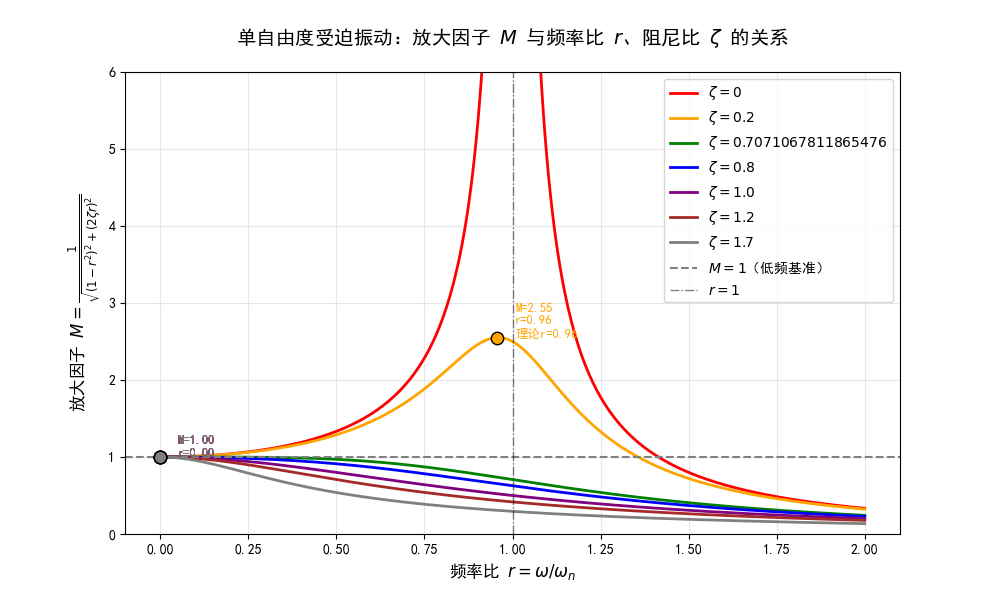
当r=1−2ζ2r=\sqrt{1-2\zeta^2}r=1−2ζ2的时候,MMM达到最大值:
Mmax=M∣r=1−2ζ2=12ζ1−ζ2M_{max}=M|_{r=\sqrt{1-2\zeta^2}}=\frac{1}{2\zeta\sqrt{1-\zeta^2}}Mmax=M∣r=1−2ζ2=2ζ1−ζ21
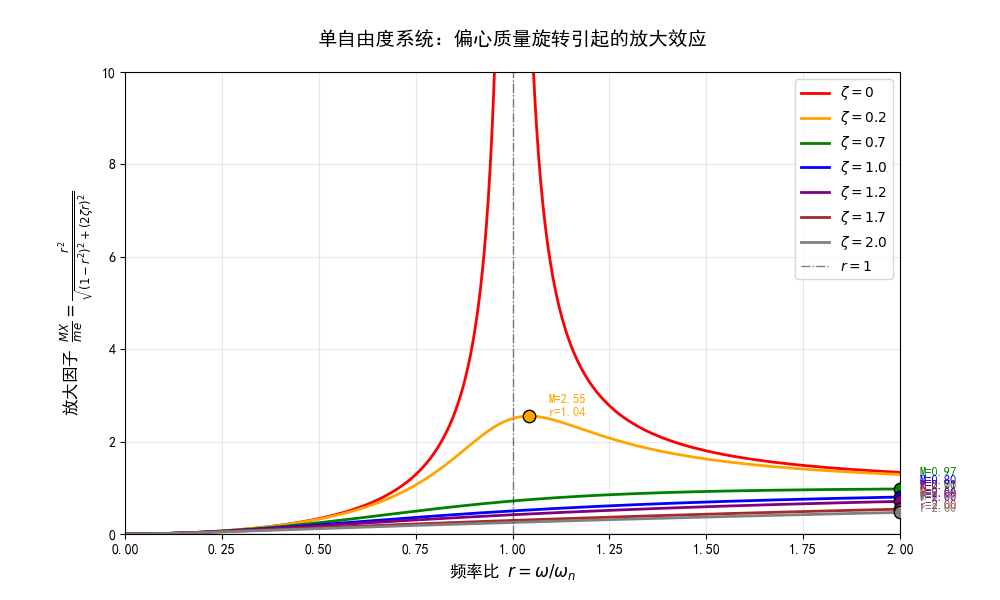
旋转不平衡质量引起的强迫振动

如图是一个质量MMM的系统,其中mmm的偏心质量绕某点旋转,偏心距离为eee,对M−mM-mM−m分析则这个系统的运动微分方程为:
(M−m)d2xdt2+md2dt2(x+esinωt)+cdxdt+kx=0\left(M-m\right)\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+m\frac{\mathrm{d}^2}{\mathrm{d}t^2}\left(x+e\sin\omega t\right)+c\frac{\mathrm{d}x}{\mathrm{d}t}+kx=0(M−m)dt2d2x+mdt2d2(x+esinωt)+cdtdx+kx=0
整理后得到:
Mx¨+cx˙+kx=meω2sinωtM\ddot{x}+c\dot{x}+kx=me\omega^2\sin\omega tMx¨+cx˙+kx=meω2sinωt
容易得到特解:
x~(t)=Im[meω2k(1−r2)2+(2ζr)2ej(ωt−arctan2ζr1−r2)]=meω2k(1−r2)2+(2ζr)2sin(ωt−arctan2ζr1−r2)=mMer2(1−r2)2+(2ζr)2sin(ωt−arctan2ζr1−r2)\begin{align*} \widetilde{x}(t)&=\text{Im}\left[\frac{\frac{me\omega^2}{k}}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}e^{j\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right)}\right]\\ &=\frac{\frac{me\omega^2}{k}}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}\sin\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right)\\ &=\frac{\frac{m}{M}er^2}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}\sin\left(\omega t-\arctan\frac{2\zeta r}{1-r^2}\right) \end{align*}x(t)=Im[(1−r2)2+(2ζr)2kmeω2ej(ωt−arctan1−r22ζr)]=(1−r2)2+(2ζr)2kmeω2sin(ωt−arctan1−r22ζr)=(1−r2)2+(2ζr)2Mmer2sin(ωt−arctan1−r22ζr)
那么这一波的放因子定义为:
MXme=r2(1−r2)2+(2ζr)2\frac{MX}{me}=\frac{r^2}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}meMX=(1−r2)2+(2ζr)2r2
对其数值仿真如图所示:
基础运动引起的强迫振动
如图为基础运动引起的强迫振动示意图,首先是机架以y=Ysinωty=Y\sin{\omega t}y=Ysinωt的形式振动,可知系统的运动微分方程:
mx¨=−k(x−y)−c(x˙−y˙)m\ddot{x}=-k(x-y)-c(\dot{x}-\dot{y})mx¨=−k(x−y)−c(x˙−y˙)
这个方程转化为:
mx¨+cx˙+kx=cy˙+kym\ddot{x} +c\dot{x} +kx =c\dot{y}+kymx¨+cx˙+kx=cy˙+ky
任然使用拓展到复数域的方法,设:
{YejωtX~(t)=Xejωt\begin{cases} Ye^{j\omega t}\\ \widetilde{X}(t)=Xe^{j\omega t} \end{cases} {YejωtX(t)=Xejωt
不拿求出特解:
X~(t)=Y1+(2ζr)2(1−r2)2+(2ζr)2ej(ωt−arctan2ζr31−r2+4ζ2r2)\widetilde{X}(t)=Y\sqrt{\frac{1+(2\zeta r)^2}{(1-r^2)^2+(2\zeta r)^2}}e^{j\left(\omega t -\arctan \frac{2\zeta r^3}{1-r^2+4\zeta^2r^2}\right)}X(t)=Y(1−r2)2+(2ζr)21+(2ζr)2ej(ωt−arctan1−r2+4ζ2r22ζr3)

非简谐激励强迫振动
周期激励下的强迫振动
各激励力的共同作用引起的线性系统响应与各激励力的分作用引起的线性系统响应和。对于满足傅里叶展开条件的函数,可以以TTT展开:
F(t)=A0+∑k=1∞[Akcos(kω0t)+Bksin(kω0t)]F(t) = A_0 + \sum_{k=1}^{\infty} \left[ A_k \cos(k\omega_0 t) + B_k \sin(k\omega_0 t) \right] F(t)=A0+k=1∑∞[Akcos(kω0t)+Bksin(kω0t)]
其中
A0=1T∫t0t0+TF(t)dtA_0 = \frac{1}{T} \int_{t_0}^{t_0+T} F(t) \, \mathrm{d}t A0=T1∫t0t0+TF(t)dt
Ak=2T∫t0t0+TF(t)cos(kω0t)dt(k=1,2,…)A_k = \frac{2}{T} \int_{t_0}^{t_0+T} F(t) \cos(k\omega_0 t) \, \mathrm{d}t \quad (k=1,2,\dots)Ak=T2∫t0t0+TF(t)cos(kω0t)dt(k=1,2,…)
Bk=2T∫t0t0+TF(t)sin(kω0t)dt(k=1,2,…)B_k = \frac{2}{T} \int_{t_0}^{t_0+T} F(t) \sin(k\omega_0 t) \, \mathrm{d}t \quad (k=1,2,\dots)Bk=T2∫t0t0+TF(t)sin(kω0t)dt(k=1,2,…)
对每一个激励都进行计算,进而求和得到最后结果。
x(t)=A02k+∑n=1∞Ank(1−rn2)2+(2ζrn)2cos(nωt−φn)+∑n=1∞Bnk(1−rn2)2+(2ζrn)2sin(nωt−φn)\begin{aligned} x(t) =& \frac{A_0}{2k} + \sum_{n=1}^{\infty} \frac{A_n}{k \sqrt{(1 - r_n^2)^2 + (2\zeta r_n)^2}} \cos(n\omega t - \varphi_n) \\ &+ \sum_{n=1}^{\infty} \frac{B_n}{k \sqrt{(1 - r_n^2)^2 + (2\zeta r_n)^2}} \sin(n\omega t - \varphi_n) \end{aligned}x(t)=2kA0+n=1∑∞k(1−rn2)2+(2ζrn)2Ancos(nωt−φn)+n=1∑∞k(1−rn2)2+(2ζrn)2Bnsin(nωt−φn)
其中,rn=nrr_n=nrrn=nr,φn=arctan2ζrn1−rn2\varphi_n=\arctan\frac{2\zeta r_n}{1-r_n^2}φn=arctan1−rn22ζrn。
一般激励下的系统响应
一般激励力下的系统响应
x(t)=1mωd∫0tF(τ)e−ζωn(t−τ)sinωd(t−τ)dτx(t) = \frac{1}{m\omega_d} \int_{0}^{t} F(\tau) \mathrm{e}^{-\zeta\omega_n (t - \tau)} \sin\omega_d (t - \tau) \mathrm{d}\tau x(t)=mωd1∫0tF(τ)e−ζωn(t−τ)sinωd(t−τ)dτ
一般基础运动激励下的系统响应
x(t)=1mωd∫0t[cy˙(τ)+ky(τ)]e−ζωn(t−τ)sinωd(t−τ)dτx(t) = \frac{1}{m\omega_d}\int_{0}^{t} \left[c\dot{y}(\tau) + ky(\tau)\right]\mathrm{e}^{-\zeta\omega_n(t - \tau)}\sin\omega_d(t - \tau)\mathrm{d}\taux(t)=mωd1∫0t[cy˙(τ)+ky(τ)]e−ζωn(t−τ)sinωd(t−τ)dτ
