运筹学——整数规划之0-1型整数线性规划，分支定界法，割平面法

整数规划问题的提出

由于在实际应用中，通常会遇到解必须是整数才符合要求，因此，对求最优整数解的问题就要单独讨论了。比如集装箱装运输货物，因为有体积和重量的限制，所以在最后的求解中，若是求得了一个小数，就不符合实际问题，由此就引出整数线性规划问题解的特点。

整数规划问题解的特点

在原来的可行解集合中加上了一个决策变量取整的约束条件，因此，整数规划问题的解一定是松弛问题可行解集合的一个子集。松弛问题的可行域是一个凸集，但是整数线性规划问题的可行域不一定是凸集。

整数线性规划的分类

1，若要求所有的变量都限制为（非负）整数，就称作纯整数线性规划，或者全整数线性规划。
2，若只要求一部分变量限制为整数，那么就叫做混合整数规划。
3，特殊的是，变量取值只能取0，或者1，这就是0-1规划。

0-1 型整数线性规划

变量只能取0或1，就是0-1型整数规划

建模方法：

若有m个互相排斥的约束条件，a_i1x₁ + a_i2x₂ + ···+a_inx_n ≤b_i，i=1,2,3···m
要想使得这些约束条件只有一个成立，那么就需要引入m个0-1变量y_i（I，2,3，···m)和一个充分大的数M，所有就有：
a_i1x₁ + a_i2x₂ + ···+a_inx_n ≤b_i+y_iM，i=1,2,3···m
并且，引入的m个变量和原变量之间有如下关系：
y₁ + y₂+ ···+y_m= m -1

因为只能有一个式子成立，所以只能有一个y_i 为0 ，其他均为1，因此y_i之和就是m-1，

举例：
某工厂用集装箱托运甲乙两种货物，每箱的体检、重量、可获利润、以及托运所受限制情况如表所示：

货物	体积（m³/箱）	重量（100kg/箱）	利润（100元/箱）
甲	5	2	20
乙	4	5	10
托运限制	车运24m³	1300kg

车运的体积限制为：5x₁ + 4x₂ ≤ 24
船运的体积限制为：7x₁ + 3x₂ ≤ 45

求：两种货物托运多少箱能够利润最大？
解：
引入一个0-1变量y表示托运方式：

假设x₁,x₂分别表示甲乙两种货物运输的数量，此时，对于运输方式就有如下方程：
5x₁ + 4x₂ ≤ 24 + y M（车辆运输的限制）
7x₁ + 3x₂ ≤ 45 + (1-y) M（船运输的限制）
其中，M是充分大的数。
（观察发现y=0时，第二个式子有效，y=1时，第一个式子有效）
上面的例子是≤的类型，若是≥的类型，就更改y前的符号：
5x₁ + 4x₂ ≥ 24 - y M
7x₁ + 3x₂≥ 45 - (1-y) M
后面的步骤就和之前求解的内容一样了。

分支定界法

基本原理

通过不断的将整数规划的松弛问题的可行域划分为两个分支并利用两个分支的解来不断更新目标函数值的上下界，一直到获得整数规划的最优解为止

使用方法

先不考虑整数约束条件，解出所有的解，画出解可行域，再对每个变量分别进行约束，每增加一个约束条件，就对应得到一个新的分支，直到分解到的解满足x_i整数约束条件时停止

举个简单的例子进行说明

求解A：

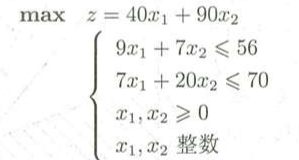
在不考虑x₁,x₂必须为整数时，解得 x₁ = 4.81, x₂ = 1.82，z₀ =356，在平面上表示A问题的可行域为：

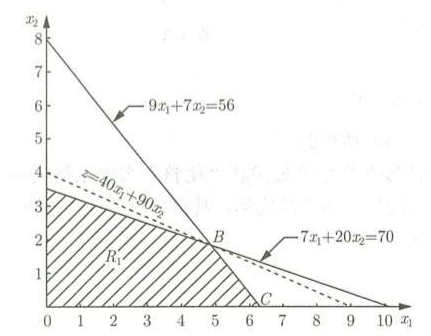
此时，这些解不符合整数的约束条件，z₀ = 356是A的目标函数值z^*d 的上界，x₁=0,x₂=0是A的一个整数可行解，对应的z=0是z^*的一个下界。
分支界定法就是基于非整数变量的解进行分支的，比如，x₁ =4.81，对原问题增加两个约束条件：x₁≤4，x₁≥5，如图：

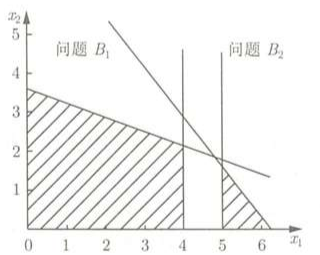
如此可以把原来的问题分解成两个子问题，也就是增加了两个分支，每一个分支上都有一个约束条件，这个过程称为第一次迭代，迭代结果如下：

B1	B2
z1 = 349	z2 = 341
x1 = 4	x1 = 5
x2 = 2.1	x2 =1.57

目前只是x₁符合整数条件，x₂没有符合整数约束条件，并且这时还没有得到全部变量是整数的解。又因为z₁ > z₂，所以z^*的上界此时换为349，就有 0 ≤ z^* ≤349，继续对B₁,B₂这两个分支再进行分解，由上表可知z₁ > z₂，所以先分解B₁，增加对x₂的约束条件，x₂≤2，x₂≥3，分别为B₃，B₄，这是第二次迭代，然后再分解B₂，增加约束条件 x₂ ≤ 1，x₂ ≥ 2，依次进行分解下去，就可以得到这个整数规划问题的最优解为：x₁ = 4，x₂ = 2，z = 340，具体分解如下图：

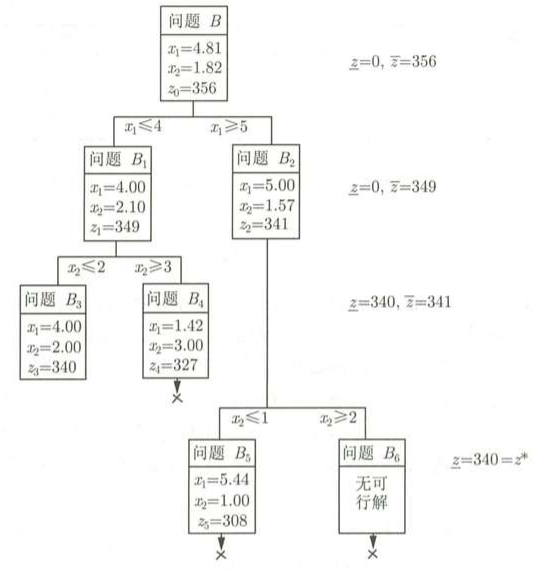
割平面法

基本原理

将松弛问题的可行域进行分割，不满足整数约束条件的最优解逐步进行剥离，直到剩下的可行域中最优解是整数为止。这个逐步递进的过程姚满足：
1，剥离出不符合整数要求的线性规划最优解
2，凡是整数的可行解都要保留

使用方法

先不考虑x_i整数约束这一条件，先按普通的方式解出所有的解，若得到的不是整数最优解，就增加能割去非整数解的线性约束条件，使得原可行域中能够切割掉一部分，并且割去的部分只能包含非整数解，没有切割掉任何整数可行解，这个过程就叫割平面

举个简单的例子加以说明
求解以下线性规划问题：

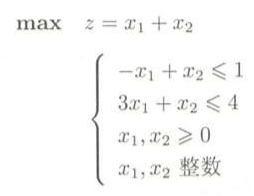
不考虑x₁，x₂的整数约束条件，得到的解为：x₁ = 3/4，x₂ = 7/4，max z = 10/4，对应图中的可行域R里面的极点A，虽然是最优解，但是不符合整数约束条件

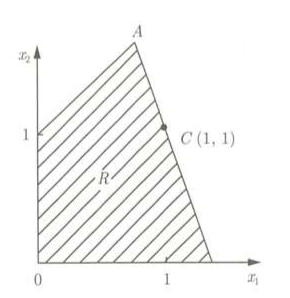
接下来的工作就是找到一条直切割线CD，把可行域R区去掉非整数部分，并且切割后恰好在边界，这样就可以得到原来问题的整数最优解，如下图：

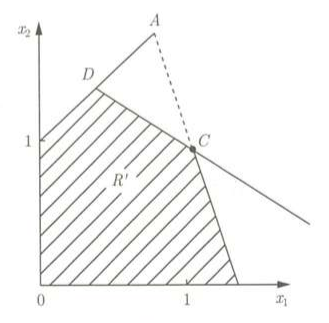
此时，我们在原问题中增加两个非负松弛变量x₃，x₄，使其变成等式约束：

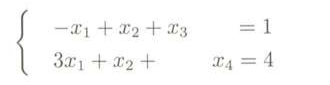
这时，用单纯形表来解出这个方程：

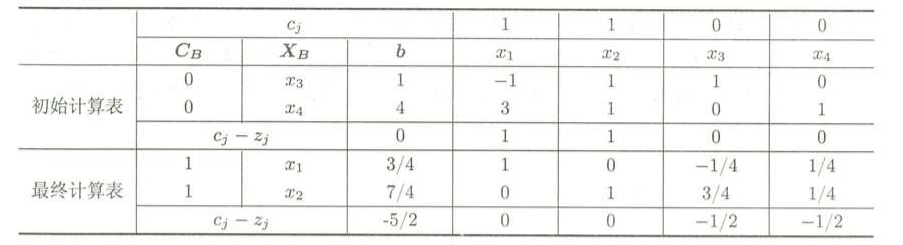
此时就得到最优解是：x₁ = 3/4，x₂ = 7/4，x₃ = x₄ = 0，z = 5/2，不能满足整数最优解的要求，按照表格中对于各个变量的约束，可以写出：

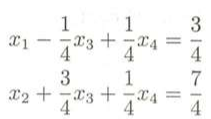
在上面关系式中，第一个式子的x₃前面是负号，所以要把这个式子的系数和常数项部分都分解为整数和非负真分数之和，第二个式子中的常数项是假分数，所以要把这个假分数的常数项分解为整数与非负真分数之和，如下：
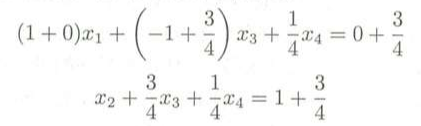把整数和分数两个部分分别进行整理：

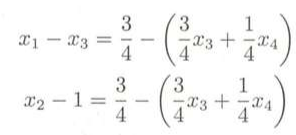
因为x₁,x₂，x₃,x₄都是非负整数，所以等式左边是整数，等式右边也应该是整数，括号里面的是正数，所以等式右边是非正数，故右边的整数值最大为零，即有：

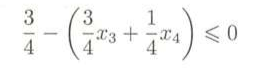
由这个方程就可以得到一个切割方程为：

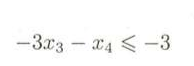
也叫做切割约束，将这个作为新增加的约束条件，那么就需要再引入一个松弛变量x₅，得到等式：

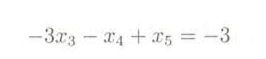
把这个新增的约束方程添加到单纯形表里，得到：

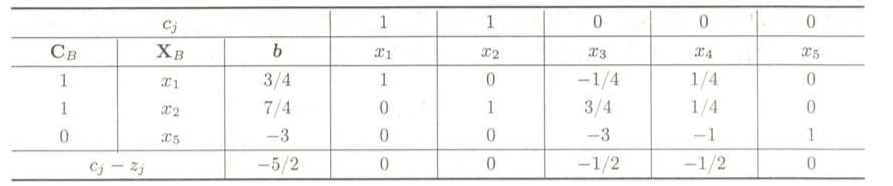
从b列可以看出x₁ = 3/4，x₂ = 7/4，都不是整数，x₅ = - 3 ，是负数，因此这时得到的解就是非可行解，用对偶单纯形法继续进行计算，最终的单纯性表如下：

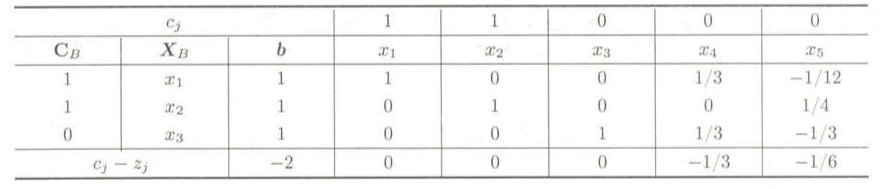
这时，x₁ = 1，x₂ = 1，x₃ = 1 ，这三个都是整数，那么这个解就是可行解。

割平面方法解决线性规划问题的步骤总结
1，先忽略整数约束条件，用单纯形表求出线性规划的最优解
2，引入松弛变量，或者是剩余变量，将不等式约束变成等式约束，等式约束作为新的约束条件，再放入单纯形表中求解
3，把得到的非整数的最优解进行分解，分解为整数和非负真分数两个部分，并分别放在等式的左右两端
4，等式左右两端应该均为非负整数，所以等式右端的部分最大为0，这样就可以得到一个不等式：（等式右端部分）≤0，这个约束方程就是切割方程，或者叫做切割约束
5，切割方程中再引入一个变量，将不等式约束变为等式约束，这个新的等式方程再加入单纯形表中进行计算，一直到最终的解全部为整数解为止。

未完代更