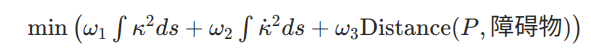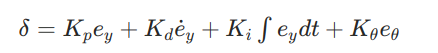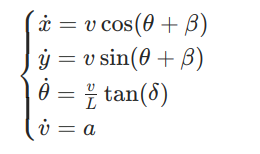当前位置：首页 > news >正文

路径平滑连接方法

news 2025/9/27 11:31:52

问题描述：

当目标路径 A 和 B 在过渡处存在横向偏差时，可通过以下方法实现平滑连接，避免控制模块出现方向盘抖动。

解决方案思路：

解决方案思路：
路径平滑：在两条路径的过渡段之间插入一条平滑的曲线，使得横向偏差被平滑过渡。常用的曲线有多项式曲线（如五次多项式）、贝塞尔曲线、样条曲线等。
控制方案：采用基于路径跟踪的控制算法，如纯跟踪（Pure Pursuit）或模型预测控制（MPC），并在过渡段考虑横向误差和航向误差的平滑变化。
具体步骤：
一、路径平滑方法
假设我们有两段路径，分别用路径A和路径B表示，它们在过渡点附近有横向偏差。我们可以在两段路径之间设计一个过渡路径，将两条路径连接起来。
常用方法：
使用多项式插值（如三次样条或五次多项式）来连接两个路径段。五次多项式可以保证位置、速度和加速度（即曲率）的平滑性。
设定过渡段的起始状态（从路径A的终点取状态：位置、方向、曲率）和终止状态（到路径B的起点取状态），然后利用五次多项式生成一条平滑的过渡曲线。
使用贝塞尔曲线或样条曲线。贝塞尔曲线可以通过控制点来调整曲线形状，且计算效率高。
二、控制方案
在生成平滑路径后，我们需要一个控制方案来保证车辆能够平滑地跟踪这条路径，特别是在过渡段。
纯跟踪控制（Pure Pursuit）：
纯跟踪控制基于车辆当前位姿和路径上的目标点（look-ahead point）来计算前轮转角。通过调整前瞻距离，可以控制跟踪的平滑性。
在过渡段，可以自适应地调整前瞻距离：在曲率较大的地方减小前瞻距离以提高跟踪精度，在曲率较大的过渡段，减小前瞻距离可以避免过冲，但可能会引起抖动，所以需要平衡。也可以采用变前瞻距离的纯跟踪算法。
模型预测控制（MPC）：
MPC通过求解一个有限时域的最优控制问题，能够考虑车辆的动力学约束和路径跟踪要求。由于MPC可以处理路径的曲率变化和车辆状态，因此在过渡段可以生成平滑的控制指令。
在MPC的代价函数中，我们可以加大对于转向变化率的权重，以抑制方向盘的抖动。
斯坦利控制（Stanley）：
斯坦利控制是一种基于横向误差和航向误差的控制方法，通过非线性反馈律计算转向角。为了平滑过渡，可以对斯坦利控制律进行改进，例如对误差进行滤波或引入积分项以减少稳态误差。
三、综合考虑
为了最大限度地减少方向盘抖动，我们可以在路径平滑和控制算法两个方面同时采取措施：
路径平滑：确保过渡段的曲率连续且变化平缓，避免曲率的突变。
控制方案：采用预测控制（如MPC）或者改进的纯跟踪控制，并考虑以下因素：
- 在控制算法中加入转向角变化率的限制，避免方向盘快速变化。
- 使用滤波器（如低通滤波器）对计算出的转向角指令进行平滑处理。
推荐方案：
路径平滑：使用五次多项式曲线连接两段路径，保证位置、方向和曲率的连续。
控制方案：采用模型预测控制（MPC），并在优化问题中考虑转向角变化率的约束，同时可以在控制输出后加入一阶低通滤波器进行平滑。
详细说明：
路径平滑步骤：
假设路径A的终点状态为（x0, y0, θ0, k0），路径B的起点状态为（x1, y1, θ1, k1）。我们使用五次多项式曲线来连接，参数为：
x(s) = a0 + a1*s + a2*s^2 + a3*s^3 + a4*s^4 + a5*s^5
y(s) = b0 + b1*s + b2*s^2 + b3*s^3 + b4*s^4 + b5*s^5
其中s为弧长参数，归一化到[0,1]。根据起点和终点的边界条件（位置、方向、曲率）求解系数。
控制方案（MPC）：
建立车辆动力学模型（如自行车模型），设计MPC控制器，其优化目标包括：
- 最小化路径跟踪的横向误差和航向误差。
- 最小化控制量（转向角）及其变化率。
约束包括：
- 车辆动力学约束。
- 转向角幅度和转向变化率的约束。
通过以上方法，可以实现在过渡段的平滑转向，避免方向盘抖动。

1. 具体实施步骤
1.1 离线路径预处理
检测过渡段：识别路径A和B的连接点
曲线拟合：插入平滑过渡曲线（长度5-15米）
曲率检查：确保最大曲率在车辆可行范围内
1.2 在线控制策略
def smooth_transition_control(current_pose, path_A, path_B):# 1. 路径选择逻辑if distance_to_transition < threshold:active_path = generate_transition_curve(path_A, path_B)else:active_path = current_active_path# 2. MPC路径跟踪control_input = mpc_controller(active_path, current_pose)# 3. 转向指令后处理smoothed_steering = low_pass_filter(control_input.steering)return apply_rate_limit(smoothed_steering)
2. 关键参数整定建议
2.1 平滑过渡参数
过渡段长度：车速×2.0-3.0秒
最大曲率变化率：＜0.1 m⁻¹/m
转向角速率限制：＜15°/s
2.2 控制器参数
MPC预测时域：3-5秒
控制权重：Δδ权重 > δ权重
滤波器截止频率：2-5 Hz
3. 验证方法
3.1 仿真测试
阶跃响应测试：验证抗抖动性能
曲率连续测试：检查路径平滑性
极端工况测试：大偏差情况下的稳定性
3.2 实车调试
逐步增加车速：从低速到高速验证
传感器反馈监测：监控实际转向角波动
主观评价：驾驶员舒适度评估
推荐方案组合
首选：Clothoid曲线过渡 + MPC控制
备选：五次多项式过渡 + 自适应纯跟踪/斯坦利控制
这种方案能有效解决方向盘抖动问题，同时保证路径跟踪精度和乘坐舒适性。

一、几何曲线连接法

1. 贝塞尔曲线插值
原理：通过调整控制点生成光滑曲线，三阶贝塞尔曲线可保证曲率连续（C²），五阶贝塞尔曲线可实现曲率导数连续（C³）。
实现步骤：
确定偏差点 P₀（路径 A 终点）和 P₃（路径 B 起点），在其外侧添加辅助控制点 P₁和 P₂，使 P₀-P₁-P₂-P₃形成控制多边形。
确保连接处切线方向一致（P₁-P₀与路径 A 末端切线平行，P₂-P₃与路径 B 起始切线平行）。
通过调整 P₁、P₂的位置优化曲线形状，避免曲率突变。
优势：灵活适配复杂几何约束，支持多段曲线拼接，适合局部路径规划。
应用案例：自动驾驶中车道变换场景，通过两段三阶贝塞尔曲线实现车道中心线的平滑过渡。
2. Clothoid 曲线（欧拉螺线）
原理：曲率随弧长线性变化，满足 G² 连续性（位置、切向、曲率连续），符合车辆转向时的角加速度特性。
参数设计：
前段 Clothoid 曲线曲率从 κ₀线性增加至中间曲率 κ_m，后段从 κ_m 线性减少至 κ₁（路径 B 曲率）。
通过 Fresnel 积分计算曲线位移和转向角，确保终点坐标与路径 B 精确对齐。
优势：显著降低高速行驶时的横向加速度变化率（jerk），提升乘坐舒适性。
工程实现：利用牛顿迭代法求解非线性方程组，确定两段 Clothoid 的弧长 L₁、L₂和中间曲率 κ_m。
3. 三次样条插值
原理：通过分段三次多项式保证 C² 连续性，插值点处的一阶导数（切向）和二阶导数（曲率）连续。
约束条件：
路径 A 终点和路径 B 起点的位置、切向、曲率必须作为边界条件输入。
中间节点的曲率变化率需平滑过渡，避免出现拐点。
优势：数学表达式简洁，计算效率高，适合实时性要求较高的场景。
局限性：若原始路径曲率变化剧烈，可能需要增加插值节点以避免振荡。

二、参数化优化方法：

1. Frenet 框架解耦优化
步骤：
将笛卡尔坐标系下的路径偏差转换为 Frenet 坐标系中的横向位移 d 和纵向位移 s。
对横向位移 d 进行五次多项式优化，确保 d、d'（横向速度）、d''（横向加速度）在过渡段连续。
结合车辆动力学约束（如最大侧向加速度）调整优化权重，生成平滑的横向轨迹。
优势：将二维路径规划问题分解为独立的一维优化，降低计算复杂度。
应用场景：高速公路弯道过渡段，通过 Frenet 框架生成符合向心加速度限制的轨迹。
2. 带约束的优化算法
目标函数：
其中，κ 为曲率，ω₁-ω₃为权重系数，分别控制路径平滑度、曲率变化率和避障优先级。
约束条件：
几何约束：路径必须经过 P₀和 P₃，且与路径 A、B 的切线方向一致。
动力学约束：曲率 κ ≤ 1 / 最小转弯半径，横向加速度 a_y ≤ μ・g（μ 为路面附着系数）。
求解方法：采用序列二次规划（SQP）或内点法迭代求解最优路径参数。

三、控制策略协同：

1. 预瞄 - 跟随 PID 控制
原理：通过预瞄距离 L_p 预测未来路径偏差，结合 PID 控制器动态调整方向盘转角。
偏差计算：
侧向偏差 e_y = 车辆当前位置到预瞄点的横向距离。
航向偏差 e_θ = 车辆航向与预瞄点切线方向的夹角。
控制律：
其中，K_p、K_d、K_i 为 PID 参数，K_θ 为航向补偿系数。
参数调整：
增大 K_p 可减小稳态偏差，但可能导致超调；增大 K_d 可抑制振荡，提升响应速度。
预瞄距离 L_p 应根据车速调整（L_p = v・T_p，T_p 为预瞄时间常数）。
2. 模型预测控制（MPC）
原理：在有限时域内预测车辆状态，滚动优化生成最优控制序列，同时考虑路径平滑性和约束。
状态方程：
其中，β 为质心侧偏角，L 为轴距，a 为纵向加速度。
优化目标：
最小化路径跟踪误差、方向盘转角变化率（避免机械磨损）和能耗。
约束条件包括转向角范围、轮胎侧偏刚度限制等。

四、工程实践要点：

误差容限设计：
根据车辆类型和行驶速度，设定最大允许横向偏差（如 ±0.2m），超过时触发路径重规划。
采用滑动窗口滤波处理传感器数据，减少高频噪声对路径生成的影响。
多算法融合：
全局路径规划采用 A或 Hybrid A生成粗略路径，局部路径优化使用 Clothoid 曲线或五次多项式。
结合 Reeds-Shepp 曲线处理需要倒车的场景，如停车场入库。
实时性保障：
采用并行计算架构（如 GPU 加速）提升优化算法速度，确保控制周期≤50ms。
对计算资源受限的嵌入式系统，可预先离线计算常见过渡段的最优参数表。

五、典型应用场景：

高速公路匝道连接：
使用 Clothoid 曲线连接主线与匝道，曲率从 0 线性增加至匝道设计值，确保车辆以恒定角加速度转向。
配合预瞄 - 跟随 PID 控制，将方向盘转角变化率限制在 0.5°/s 以内，避免乘客晕车。
城市道路交叉口转向：
采用五阶贝塞尔曲线平滑连接直道与弯道，通过优化控制点使曲率变化率≤0.02 rad/m²。
结合 MPC 预测对向车辆轨迹，动态调整路径以保持安全距离。
工业 AGV 路径纠偏：
当激光雷达检测到路径偏差时，触发三次样条插值生成修正路径，同时通过 PID 控制器调整电机转速差。
预瞄距离设为 AGV 轴距的 1.5 倍，确保转向平稳性。
通过上述方法，可在保证路径几何连续性的同时，满足车辆动力学约束，有效抑制方向盘抖动。实际应用中需根据具体场景选择合适的算法组合，并通过实车测试优化参数，以达到最佳控制效果。