【生成式模型】VAE变分自编码器分析

概念分析

众所周知，我们可以用足够多的高斯分布去拟合任意同维度的函数
即
$$P(x)=\sum _{m}P(m)P(x\mid m)$$
其中$P(x\mid m)$表示编号为m的高斯分布，$P(m)$表示该高斯分布被采样到的概率

进一步的，我们将离散的高斯分布换成大量连续的高斯分布（即服从某一连续分布的高斯分布）
$$P(x)={\int }_{z}P(z)P(x\mid z)dz$$

因此，编码器Decoder主要任务是拟合$\mu (z)$和$\sigma (z)$，即拟合出每个高斯分布的高斯分布（当然也可以是别的分布，这里以高斯分布举例），最终得到对目标对象的拟合

简单来讲

假设目标对象为X和潜变量为Z，
其中，目标对象可以是任何可以用函数表达的集合，比如一幅画（RGB编码），一句话（ASCII编码），一段音频（傅里叶变换）等；
但是用这些编码来表达对象时过于复杂

因此，我们注意到：P(Z|X)可用于实现encoder，P(X|Z)可用于实现decoder
（规范地讲，在VAE中，用Q(Z|X)表示encoder，用P(X|Z)表示decoder）
所谓encoder，就是输入目标对象，返回一个潜向量，潜向量本身并不具有可解释性，它更类似于encoder和decoder之间的“暗号”，但是我们也可以认为这个潜向量就是该对象在低维度的潜在表示
而decoder的意义就是在拿到encoder的“暗号”后，将其还原成一个完整的对象；当然了，既然是有损压缩后解压，最后得到的对象和原对象肯定有区别；
当然了，在生成式模型中，我们要的就是这个“不一样”，如此才能让生成的内容具有多样性

更进一步

从上面来看，VAE似乎只能用于模仿：生成相似的画或者音频等；但事实上，VAE可以做到跨模态生成。

因为VAE 并没有要求输入和输出必须一致，约束只是：潜变量 z 同时捕捉了输入模态和输出模态的关键信息
只要能定义出合适的 似然模型 $p_{\theta }(y\mid z)$，就可以让 Decoder 生成任意类型的数据（图像、语音、文本、特征向量…）
换句话说，Encoder 负责“推断潜变量”，Decoder 负责“生成目标数据”，两边的数据类型可以不一样

实操

用KL散度衡量两个分布的差异，并以此构建损失函数

证据下界（ELBO）有如下关系：（过程不管，只需要知道）
$$\log p_{\theta }(x)=ELBO(x)+KL(q_{\varphi }(z|x)\Vert p_{\theta }(z|x))$$
其中：

• $q_{\varphi }(z|x)$：近似后验，由 encoder 给出
• $p_{\theta }(x|z)$：生成模型，由 decoder 给出
• $p(z)$：潜变量的先验

则有：

• 右边第二项是真实后验 $p_{\theta }(z|x)$ 和近似后验 $q_{\varphi }(z|x)$ 的 KL 散度
• 因为 KL 散度非负，所以 ELBO ≤ $\log p_{\theta }(x)$
• 优化时，我们最大化 ELBO，相当于：
  • 尽量让重构项大（数据能重构得好）；
  • 同时让 KL 散度项小（近似后验 $q_{\varphi }(z|x)$ 靠近真实后验）。

一言以蔽之：ELBO 最大化 ↔ 真实后验 $p_{\theta }(z|x)$ 与近似后验 $q_{\varphi }(z|x)$ 更接近，也就是拟合的和实际的更加接近

什么是ELBO

我们想最大化观测数据的对数似然：

$$\log p_{\theta }(x)=\log \int p_{\theta }(x,z)dz$$

但这个积分往往不可解（高维、非线性），无法直接得到
因此，引入一个容易采样的分布 $q_{\varphi }(z|x)$（近似后验），通过 Jensen 不等式可以得到：

$$\log p_{\theta }(x)=\log \int q_{\varphi }(z|x)\frac{p_{\theta }(x,z)}{q_{\varphi }(z|x)}dz\ge {\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x,z)-\log q_{\varphi }(z|x)]$$
右边这个期望，就是 ELBO：
$$\text{ELBO}(x)={\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]-KL(q_{\varphi }(z|x)\Vert p(z))$$
其中：

• 第一项（重构项）
  ${\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]$
  → 保证从潜变量 $z$ 解码出来的 $x$ 尽可能接近真实输入。

• 第二项（KL 正则项）
  $-KL(q_{\varphi }(z|x)\Vert p(z))$
  → 约束近似后验分布不要偏离先验 $p(z)$，让潜在空间结构化、可采样。

如何最大化ELBO

由于需要最大化，因此我们沿ELBO的负梯度方向迭代
$$\mathcal{L}(x)=-{\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]+KL(q_{\varphi }(z|x)\Vert p(z))$$
那么如何求这两项呢？

第一项：重构损失Reconstruction Loss

$${\mathcal{L}}_{recon}=-{\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]$$
这一项代表了重构损失。它的直观意义是：从后验分布 $q_{\varphi }(z|x)$ 中采样一个隐变量 $z$，然后用这个 $z$ 通过解码器 $p_{\theta }(x|z)$ 重构出原始输入 $x$。我们希望重构出来的 $\hat{x}$ 与原始的 $x$ 尽可能一致。$-\log p_{\theta }(x|z)$ 就是衡量这种一致性的损失。期望 $\mathbb{E}$ 表示我们希望对于所有可能的 $z$（从编码器结果中采样）都能很好地重构。

直接计算这个期望通常不太可能，因此我们通常使用蒙特卡洛采样来近似它。
在实践中，为了简化计算，每个数据点通常只采样一次（$L=1$），具体实现如下：

• 编码 (Encoding): 将输入数据 $x$ 送入编码器网络（由参数 $\varphi$ 定义），然后输出该x对应的z的分布参数，比如，如果我们认为z应当服从高斯分布，则此时应该得到该分布的均值 ${\mu }_x$ 和对数方差 $\log ({\sigma }_x^2)$。编码器的作用是学习后验分布 $q_{\varphi }(z|x)$。
• 采样 (Sampling) with Reparameterization Trick: 我们需要从 $q_{\varphi }(z|x)=\mathcal{N}(z;{\mu }_x,{\sigma }_x^2)$ 中采样一个 $z$。但直接采样是随机操作，梯度无法回传。因此我们使用重参数技巧：
  1. 从标准正态分布 $\mathcal{N}(0,I)$ 中采样一个随机噪声 $ϵ$。
  2. 计算隐变量 $z={\mu }_x+{\sigma }_x\odot ϵ$。（其中 ${\sigma }_x=\exp (0.5\cdot \log ({\sigma }_x^2))$）
     这样，随机性被转移到了 $ϵ$ 上，而 $z$ 的计算过程对于 ${\mu }_x$ 和 ${\sigma }_x$ 是可导的。
• 解码 (Decoding): 将采样得到的 $z$ 送入解码器网络（由参数 $\theta$ 定义），得到重构的输出 $\hat{x}$。
• 计算损失: 损失的具体形式取决于输入数据 $x$ 的类型：
  • 对于二值数据 (Binary Data)，如 MNIST 手写数字（像素值为0或1）：我们假设 $p_{\theta }(x|z)$ 是一个伯努利分布 (Bernoulli distribution)。此时，负对数似然等价于二元交叉熵 (Binary Cross-Entropy, BCE) 损失。
    $${\mathcal{L}}_{recon}=\sum _{i=1}^D-[x_i\log ({\hat{x}}_i)+(1-x_i)\log (1-{\hat{x}}_i)]$$
    其中 $D$ 是数据维度（例如图片像素总数），$x_i$ 是原始像素值，${\hat{x}}_i$ 是解码器输出的对应像素值。
  • 对于连续数据 (Continuous Data)，如经过归一化到 [0, 1] 区间的彩色图片：我们通常假设 $p_{\theta }(x|z)$ 是一个高斯分布。如果假设其方差是固定的，那么负对数似然就等价于均方误差 (Mean Squared Error, MSE) 损失。
    $${\mathcal{L}}_{recon}=\sum _{i=1}^D(x_i-{\hat{x}}_i{)}^2$$

关于采样的定义：

• 输入 x：你想找的书，比如《物种起源》。
• 编码器：图书管理员。你把书名《物种起源》告诉他，他不会让你在整个图书馆里随机乱找。他会告诉你：“这本书在三楼，科学区，第五个书架（这就是 ${\mu }_x$），那附近的书都差不多（这就是 ${\sigma }_x^2$）”。
• 采样 z：你根据管理员的指示，走到那个特定的位置，然后在那个书架上随机抽一本。你抽到的很可能是《物种起源》，也可能是它旁边的《遗传的奥秘》，但绝对不可能抽到一楼的《哈利波特》。

换句话说，采样不是在整个隐空间中（整个图书馆）随机采样 z，而是在x 决定的采样区域（哪个书架）。采样这个动作本身是随机的，但它被严格限制在 x 所定义的那个小区域内。

关于重参数部分

首先需要明确一点：当一个参数带有随机性时，它就不能求导，随机采样的结果也因随机性而带有离散的特征。
因此，重参数的核心思想是：将随机性与模型参数分离
想象一下在教一个机器人射箭。

• 旧方法（无法学习）: 你告诉机器人：“瞄准靶心位置 $\mu$，并在这个位置附近随机抖动 $\sigma$ 来射击”。机器人射出了一箭 $z$。如果射偏了，你怎么告诉机器人调整 $\mu$ 和 $\sigma$？你很难说清楚这次射偏是因为 $\mu$ 不对，还是因为随机抖动 $\sigma$ 的运气不好（因为随机性被包含在了变量中）。
• 重参数技巧（可以学习）: 你告诉机器人：“首先，在你的正前方（位置0）随机抖动一下（这相当于 $ϵ\sim \mathcal{N}(0,1)$），得到一个抖动量 $ϵ$。然后，把你的弓整体平移 $\mu$ 个单位，再把抖动的幅度缩放 $\sigma$ 倍，最后把箭射出去（$z=\mu +\sigma \cdot ϵ$）”。
  现在，如果射偏了，学习机制就非常清晰了。你可以明确地计算出：为了让最终落点 $z$ 更接近靶心，我的平移量 $\mu$ 和缩放量 $\sigma$ 应该如何调整（随机性部分因为不受控制而被排除，我们仅考虑我们可以控制的部分）。

第二项：KL 散度

$${\mathcal{L}}_{KL}=KL(q_{\varphi }(z|x)\Vert p(z))$$

• 作用：
  这一项是正则化项 (Regularization Term)。它衡量了编码器产生的后验分布 $q_{\varphi }(z|x)$ 与我们预先设定的先验分布 $p(z)$ 之间的距离。我们通常选择一个简单、易于处理的先验分布，最常见的选择是标准正态分布 $p(z)=\mathcal{N}(0,I)$。
  这一项的作用是约束编码器，使得它生成的隐变量分布在结构上趋向于一个标准正态分布，这有助于形成一个规整、连续且有意义的隐空间 (Latent Space)。

• 具体计算
  当 $q_{\varphi }(z|x)$ 是对角高斯分布 $\mathcal{N}({\mu }_x,\text{diag}({\sigma }_x^2))$，而 $p(z)$ 是标准正态分布 $\mathcal{N}(0,I)$ 时，它们之间的 KL 散度有一个解析解 (Analytical Solution)，无需采样近似。这大大简化了计算。

公式如下：
$$KL(\mathcal{N}({\mu }_x,{\sigma }_x^2)\Vert \mathcal{N}(0,I))=\frac{1}{2}\sum _{j=1}^J({\sigma }_{x,j}^2+{\mu }_{x,j}^2-\log ({\sigma }_{x,j}^2)-1)$$
其中：

• $J$ 是隐空间的维度 (dimension of latent space)。
• ${\mu }_{x,j}$ 和 ${\sigma }_{x,j}^2$ 分别是编码器输出的均值向量和方差向量的第 $j$ 个分量。

在代码实现中，我们会使用编码器输出的 ${\mu }_x$ 和 $\log ({\sigma }_x^2)$ 来计算。将 ${\sigma }_x^2=\exp (\log ({\sigma }_x^2))$ 代入即可。

关于标准正态分布

让编码器生成隐变量z的分布趋近于标准正态分布，这是非常重要的一步
简单来说：不仅要在训练时学会“重构输入”，还要在测试时“能随便采一个 z 然后生成合理的 x”

更具体的，我们需要保证潜空间是连通的、密集的，能支持平滑插值；
如果每个样本的后验 $q_{\varphi }(z|x)$ 都被约束在标准正态附近，那么整个潜在空间不会“空洞”，采样出来的点更可能生成合理的样本；

在机器人领域，前者可以保证机器人的动作具有连续性，不会从一个状态突然跳跃到另一个状态；后者保证在某一个邻域内的状态具有相似性（注意是相似而不是完全一致，这一点才真正赋予模型泛化能力）

进一步拓展

不具有解释性的模型难用且危险，因此我们需要对VAE进行升级，也就有了CVAE
简单地讲：
在 VAE 中额外引入条件变量 C（比如文本描述的向量表示）
编码器和解码器都条件化在 C 上：
$$Q(Z|X,C)andP(X|Z,C)$$
其中，C是由其他文本编码器生成的，该文本编码器需要在表达类似含义时，输出类似的向量，以确保模型的稳定性
借用论文 Learning Fine-Grained Bimanual Manipulation with Low-Cost Hardware 的图片

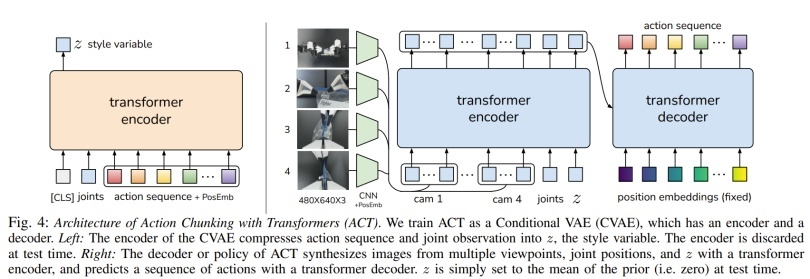
论文中，将一个VAE本身(右侧蓝色部分)作为了另一个VAE（整张图）的decoder，以此实现CVAE+跨模态VAE；
其中，语言对应的潜向量Z是右侧VAE的condition，指挥右侧VAE的跨模态生成，使其具有一定的可解释性