孤岛水流问题

本文参考代码随想录

题目描述：

现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述：

第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述：

输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

输入示例：

5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1
输出示例：

0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1

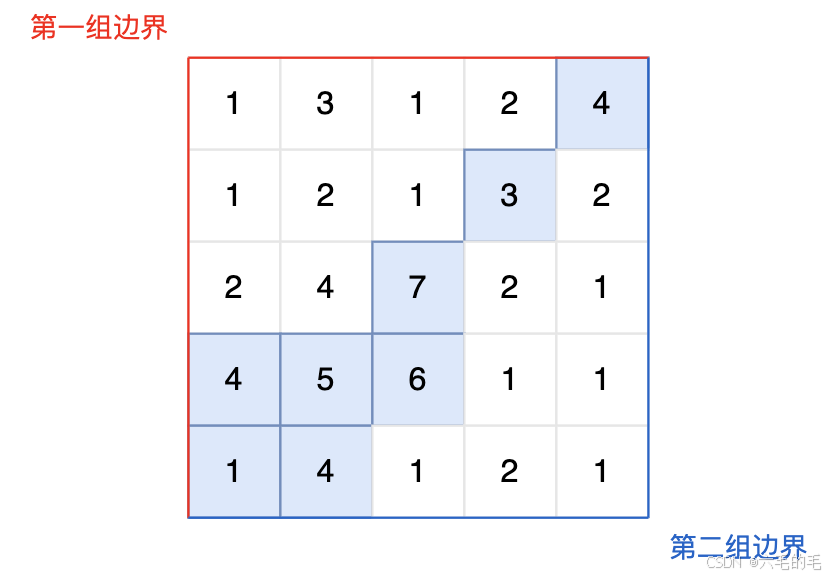
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。

数据范围：

1 <= M, N <= 50

思路

从第一组边界上的节点 逆流而上，将遍历过的节点都标记上。

同样从第二组边界的边上节点 逆流而上，将遍历过的节点也标记上。

然后两方都标记过的节点就是既可以流向第一组边界也可以流向第二组边界的节点。


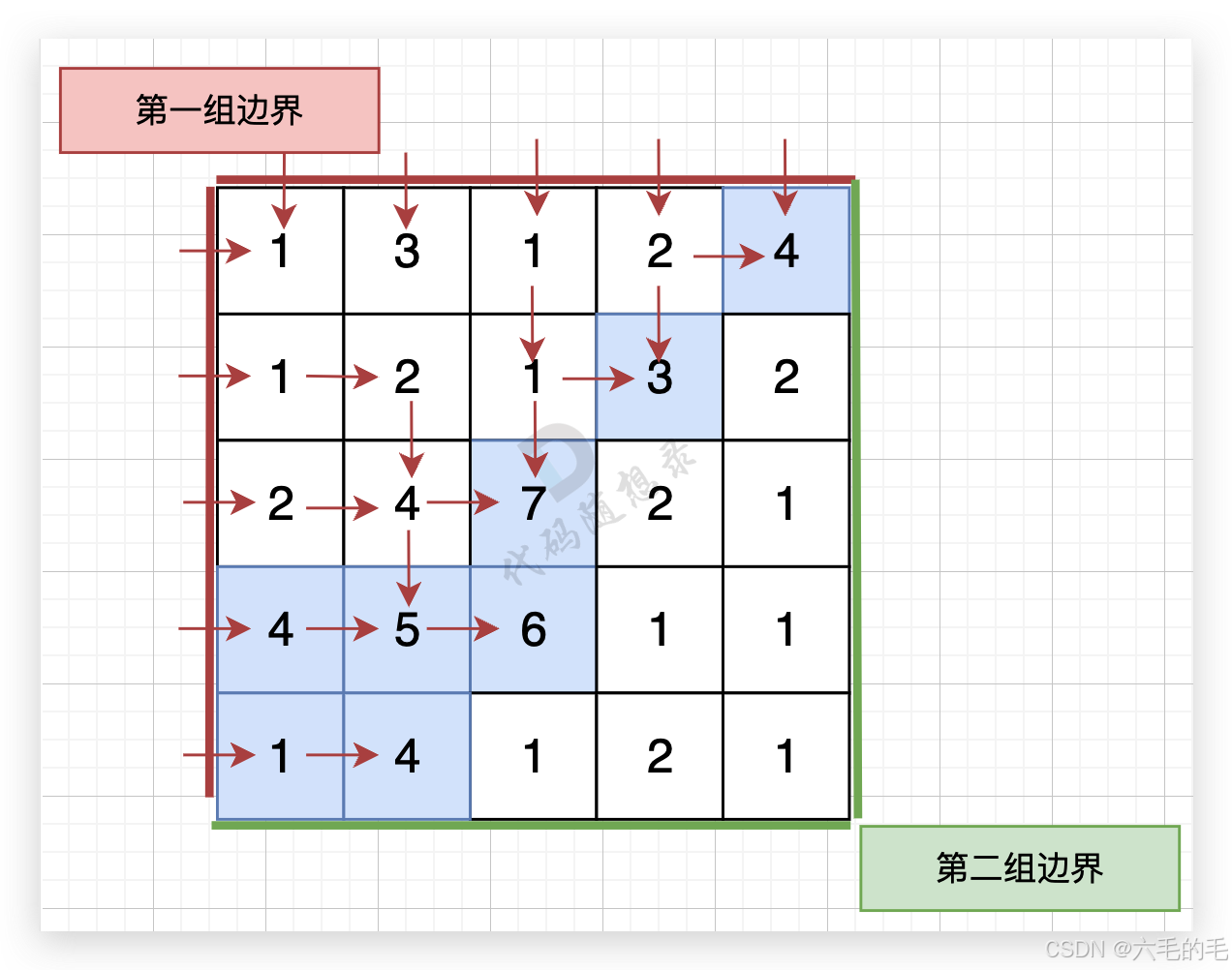
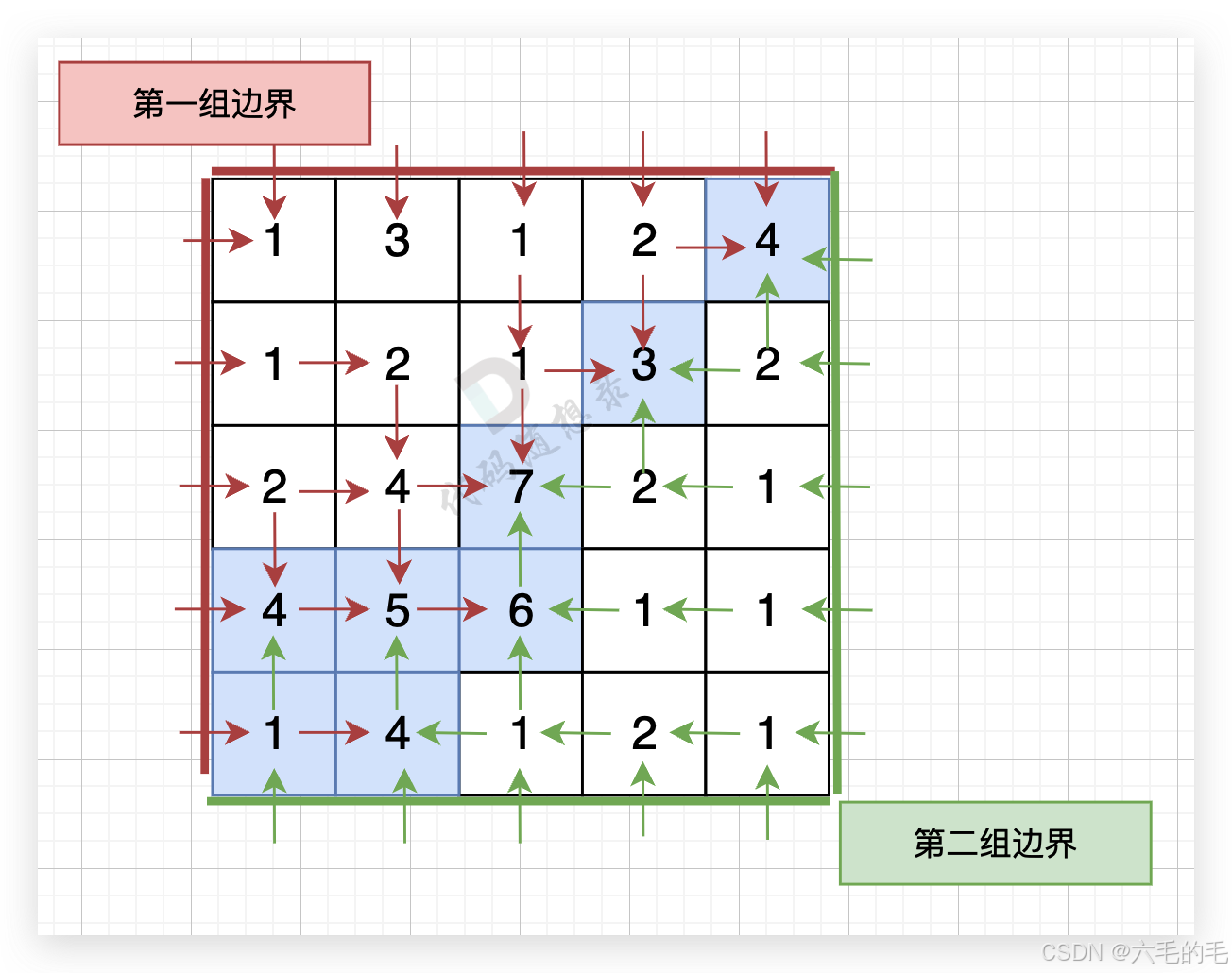
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。

#include<iostream>
#include<vector>using namespace std;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y){if(visited[x][y]) return;visited[x][y] = true;for(int i = 0; i < 4; i++){int nextx = x + dir[i][0];int nexty = y + dir[i][1];if(nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;if(grid[x][y] <= grid[nextx][nexty]){dfs(grid, visited, nextx, nexty);}}return;}int main(){int n, m;cin >> n >> m;vector<vector<int>> grid(n, vector<int>(m, 0));for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){cin >> grid[i][j];}}vector<vector<bool>> first_visited(n, vector<bool>(m, false));vector<vector<bool>> second_visited(n, vector<bool>(m, false));for(int i = 0; i < n; i++){dfs(grid, first_visited, i, 0);dfs(grid, second_visited, i, m - 1);}for(int j = 0; j < m; j++){dfs(grid, first_visited, 0, j);dfs(grid, second_visited, n - 1, j);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(first_visited[i][j] && second_visited[i][j]){cout << i << " " << j << endl;}}}
}