深度学习入门：从神经网络基础到模型训练优化

深度学习入门：从神经网络基础到模型训练优化

在人工智能飞速发展的今天，深度学习已成为推动技术进步的核心引擎之一。无论是图像识别、语音处理还是自然语言理解，背后都离不开一个关键的数学模型——人工神经网络（Artificial Neural Network, ANN）。

本文将带你从零开始，深入浅出地理解神经网络的基本构成、前向传播机制、激活函数的作用、参数初始化策略，以及如何使用 PyTorch 构建一个完整的神经网络模型，并深入探讨损失函数、反向传播与优化算法等核心训练机制。

---

一、什么是神经网络？

人工神经网络是对生物大脑神经元工作方式的一种数学模拟。它由多个相互连接的“人工神经元”组成，通过层层传递和处理信息，最终实现对复杂数据模式的学习与预测。

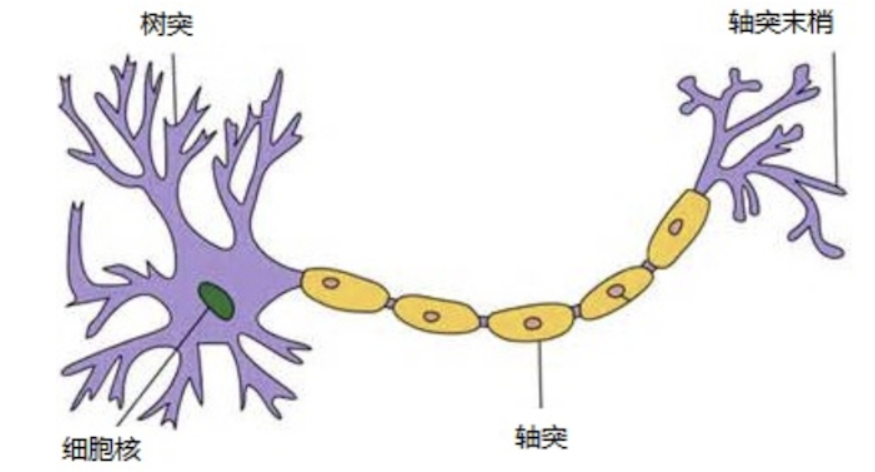
生物神经元的启发

在人脑中，神经元通过树突接收信号，细胞体对信号进行加权求和，当电位达到阈值时，轴突就会发出电信号。这一过程启发了人工神经元的设计：

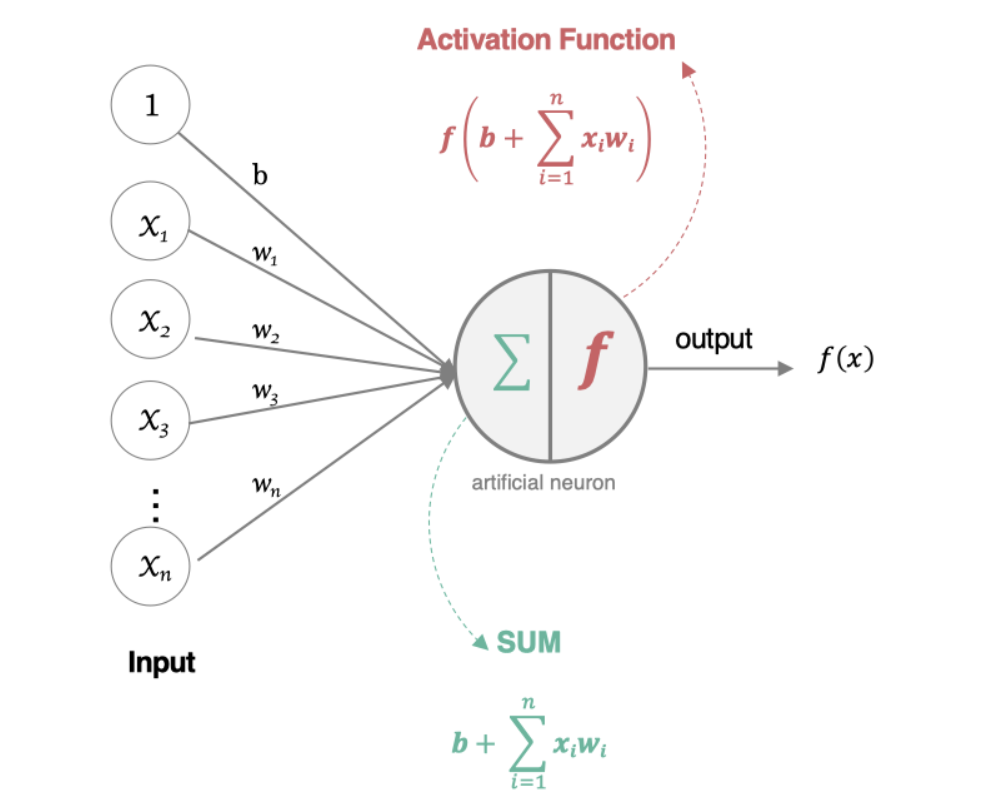
• 输入信号：相当于树突接收到的信息。
• 权重（w）：表示每个输入的重要性。
• 偏置（b）：相当于激活阈值。
• 激活函数：决定神经元是否“激活”。

---

二、神经网络的基本结构

一个典型的神经网络由三层构成：

1. 输入层（Input Layer）
   接收原始数据（如图像像素、文本向量等），每个特征对应一个神经元。

2. 隐藏层（Hidden Layers）
   位于输入层和输出层之间，负责提取数据中的高级特征。网络的“深度”即指隐藏层的数量。

3. 输出层（Output Layer）
   输出最终的预测结果，例如分类概率或回归值。
   

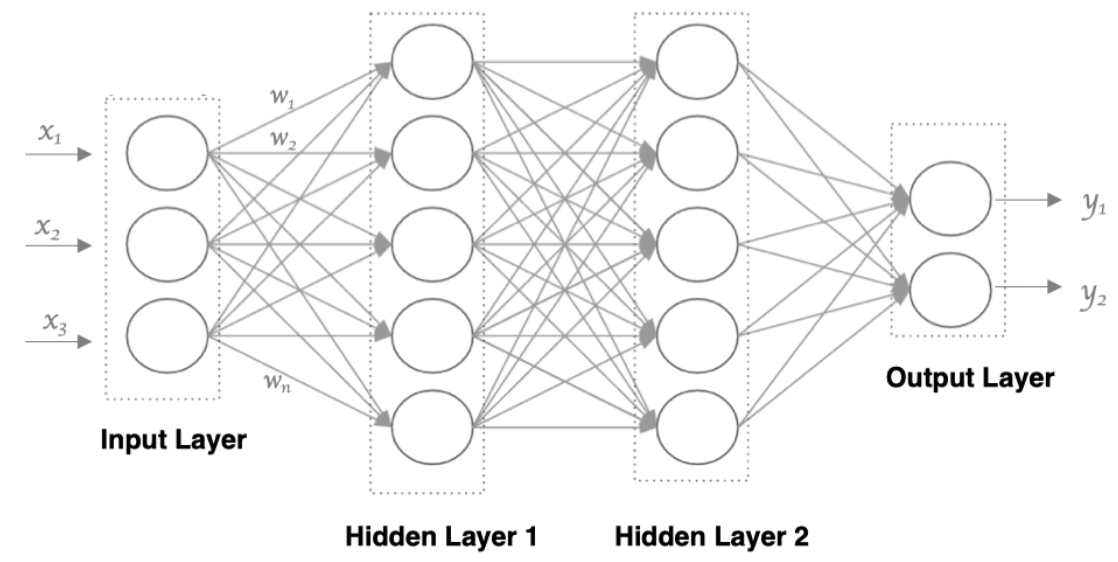
特点：

• 相邻层之间全连接（Fully Connected）
• 同一层神经元无连接
• 每条连接都有权重（w）和偏置（b）

---

三、前向传播：数据如何流动？

前向传播（Forward Propagation）是神经网络的核心计算过程。数据从输入层出发，逐层计算，直到输出层产生预测结果。

神经元内部发生了什么？

每个神经元在前向传播中会产生两个关键值：

1. 内部状态值 z
   所有输入与其对应权重的加权和加上偏置：
   $$z=w\cdot x+b$$

2. 激活值 a
   将内部状态值通过激活函数进行非线性变换：
   $$a=f(z)$$
   这个输出会作为下一层神经元的输入。

这个过程不断重复，直到最后一层输出结果。

---

四、为什么需要激活函数？

如果没有激活函数，无论网络有多少层，其本质仍然是一个线性模型。因为多个线性变换的组合依然是线性的。

激活函数的作用

• 引入非线性因素，使神经网络能够拟合任意复杂函数。
• 决定神经元是否“激活”，即是否向后传递信号。

---

常见激活函数对比

1. Sigmoid 函数

• 公式：$$\sigma (x)=\frac{1}{1+e^{-x}}$$
• 输出范围：(0, 1)
• 优点：适合二分类输出层
• 缺点：
  • 容易梯度消失（导数最大为 0.25）
  • 输出不以 0 为中心，影响收敛速度
  • 计算开销大（指数运算）
    

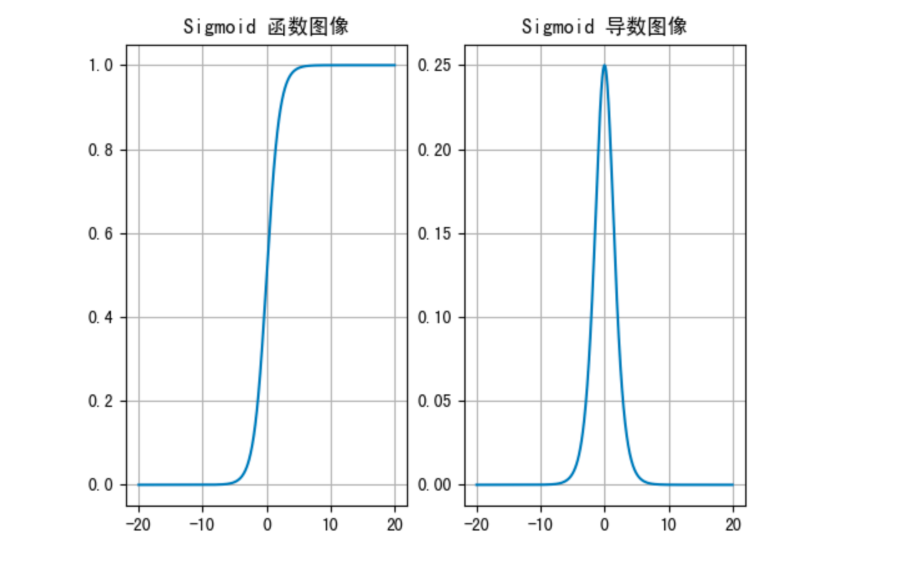
当输入值超出 [-6, 6] 时，几乎饱和，导致信息丢失。

2. Tanh（双曲正切）

• 公式：$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
• 输出范围：(-1, 1)
• 优点：以 0 为中心，收敛更快
• 缺点：仍存在梯度消失问题
  

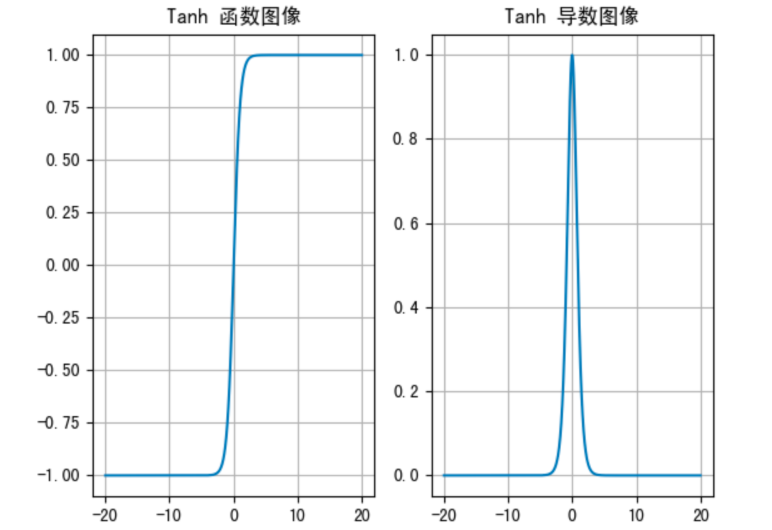
适用于隐藏层，但不如 ReLU 流行。

3. ReLU（Rectified Linear Unit）

• 公式：$$\text{ReLU}(x)=\max (0,x)$$
• 优点：
  • 计算简单，训练效率高
  • 在 x > 0 时梯度恒为 1，缓解梯度消失
  • 引入稀疏性，减少过拟合
• 缺点：
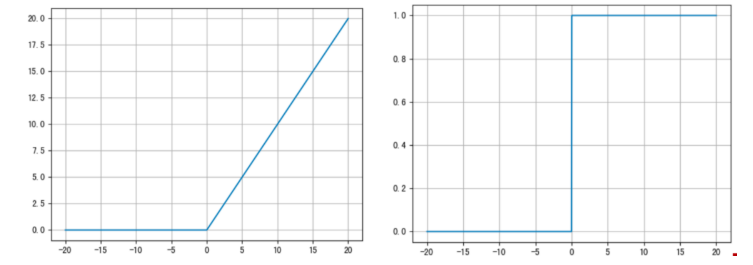
  • “死亡 ReLU”问题：某些神经元永远不激活（输出为 0）
    

目前最常用的激活函数，尤其适合深层网络。

4. Softmax（多分类输出）

• 公式：
  $$\text{Softmax}(x\_i)=\frac{e^{x\_i}}{\sum \_j{e}^{x\_j}}$$
• 作用：将输出转换为概率分布，所有输出之和为 1
• 应用场景：多分类任务的输出层

import torchscores = torch.tensor([0.2, 1.3, 3.75])
probabilities = torch.softmax(scores, dim=0)
print(probabilities)
# 输出: tensor([0.0212, 0.0638, 0.7392])

---

如何选择激活函数？

层级	推荐选择
隐藏层	ReLU（首选），Leaky ReLU（防死亡）
输出层（二分类）	Sigmoid
输出层（多分类）	Softmax
输出层（回归）	Identity（恒等函数）

尽量避免在隐藏层使用 Sigmoid。

---

五、参数初始化：为何如此重要？

神经网络训练前，权重（w）和偏置（b）需要初始化。不当的初始化会导致：

• 梯度消失：权重太小 → 梯度趋近于 0 → 无法更新
• 梯度爆炸：权重太大 → 梯度无限增长 → 训练不稳定

常见初始化方法

方法	说明
全0初始化	所有权重视为 0 → 对称问题，不可用
全1初始化	所有权重视为 1 → 同上
随机初始化（均匀/正态）	小范围随机值，但需注意尺度
Xavier 初始化	考虑输入输出维度，保持方差一致，适合 Sigmoid/Tanh
Kaiming（He）初始化	专为 ReLU 设计，推荐用于 ReLU 及其变体

现代深度学习中，优先使用 Kaiming 或 Xavier 初始化。

PyTorch 中的初始化示例

import torch.nn as nnlinear = nn.Linear(5, 3)# Xavier 初始化（正态分布）
nn.init.xavier_normal_(linear.weight)# Kaiming 初始化（ReLU 专用）
nn.init.kaiming_normal_(linear.weight, nonlinearity='relu')# 偏置通常初始化为 0 或 1
nn.init.zeros_(linear.bias)

---

六、动手实践：用 PyTorch 搭建神经网络

下面我们用 PyTorch 构建一个简单的三层神经网络：

• 第一层：Sigmoid 激活，Xavier 初始化
• 第二层：ReLU 激活，Kaiming 初始化
• 输出层：Softmax 归一化（多分类）

import torch
import torch.nn as nn
from torchsummary import summaryclass Model(nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = nn.Linear(3, 3)nn.init.xavier_normal_(self.linear1.weight)nn.init.ones_(self.linear1.bias)self.linear2 = nn.Linear(3, 2)nn.init.kaiming_normal_(self.linear2.weight, nonlinearity='relu')nn.init.ones_(self.linear2.bias)self.out = nn.Linear(2, 2)def forward(self, x):x = torch.sigmoid(self.linear1(x))x = torch.relu(self.linear2(x))x = torch.softmax(self.out(x), dim=-1)return x# 训练测试
model = Model()
data = torch.randn(5, 3)
output = model(data)print("输入形状:", data.shape)   # [5, 3]
print("输出形状:", output.shape) # [5, 2]

查看模型参数

for name, param in model.named_parameters():print(name, param.shape)

输出：

linear1.weight torch.Size([3, 3])
linear1.bias   torch.Size([3])
linear2.weight torch.Size([2, 3])
linear2.bias   torch.Size([2])
out.weight     torch.Size([2, 2])
out.bias       torch.Size([2])

模型参数总数计算

公式：对于第 $n$ 层（输入维度 $m$，输出维度 $n$），参数量为：
$$\text{Params}=m\times n+n$$

总参数数 = $3\times 3+3+3\times 2+2+2\times 2+2=26$

使用 torchsummary 验证：

summary(model, input_size=(3,))

---

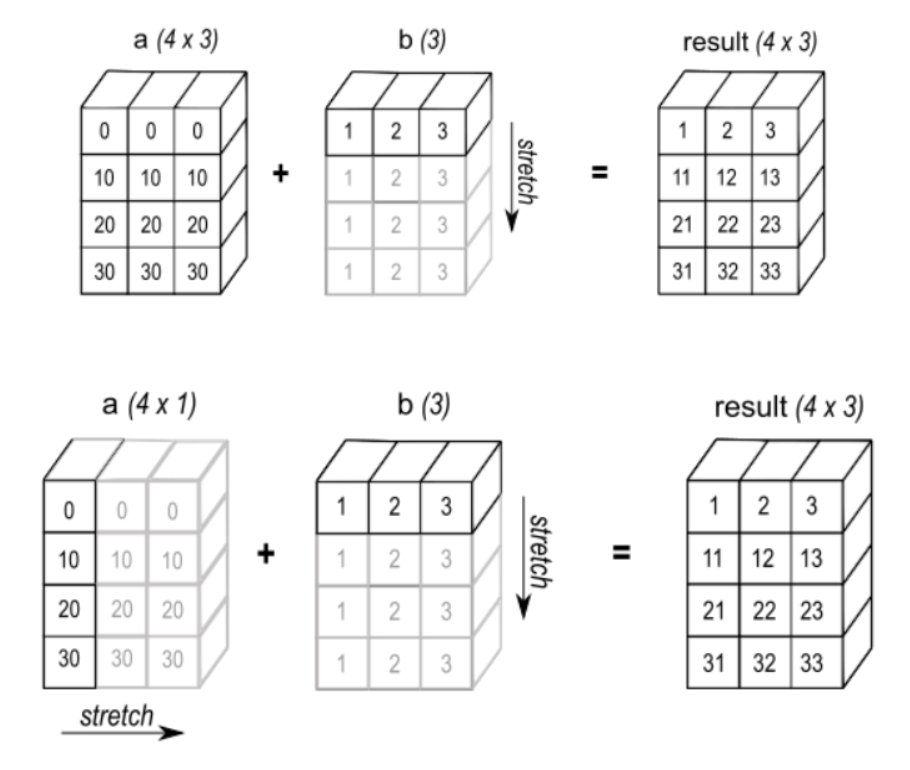
七、广播机制（Broadcasting）简介

在张量运算中，不同形状的数组有时也能相加。这得益于广播机制。

广播规则

1. 维度不足时，左侧补 1
2. 维度不匹配时，若某维度为 1，则可扩展至匹配
3. 若维度不为 1 且不相等，则报错

示例

import numpy as npa = np.array([[1, 2, 3], [4, 5, 6]])  # (2, 3)
b = np.array([1, 1, 1])                # (3,) → (1, 3) → (2, 3)
print(a + b)
# 成功广播，结果为：
# [[2 3 4]
#  [5 6 7]]

不满足广播条件的例子：

a = np.array([1, 2, 3, 4])     # (4,)
b = np.array([[1,2,3],[2,3,4]]) # (2,3)
# a + b → 报错！无法广播

---

八、损失函数：衡量模型表现的标尺

损失函数（Loss Function）是衡量模型预测值与真实值之间差异的函数。模型的目标就是最小化损失函数的值。

损失函数的核心作用

• 评估性能：反映模型预测结果与真实值的匹配程度。
• 指导优化：通过梯度下降等算法最小化损失函数，优化模型参数。

---

1. 分类任务：交叉熵损失

多分类任务（CrossEntropyLoss）

PyTorch 中使用 nn.CrossEntropyLoss()，它内部自动包含 Softmax + 负对数似然。

import torch
import torch.nn as nn# 预测值（logits）
y_pred = torch.tensor([[0.1, 0.1, 0.3, 1.4, 0.05, 0.05],[0.02, 0.08, 0.2, 0.2, 0.05, 2.45]])
# 真实标签（无需 one-hot 编码）
y_true = torch.tensor([3, 5])criterion = nn.CrossEntropyLoss()
loss = criterion(y_pred, y_true)
print("loss-->", loss)

重要提示：CrossEntropyLoss 接收的是 logits（未归一化的分数），不是概率！

二分类任务（BCELoss）

使用 Sigmoid + 二分类交叉熵。

y_true = torch.tensor([0, 1, 0], dtype=torch.float32)
y_pred = torch.tensor([0.6901, 0.5459, 0.2469])  # Sigmoid 输出loss = nn.BCELoss()
my_loss = loss(y_pred, y_true)
print('loss：', my_loss)

---

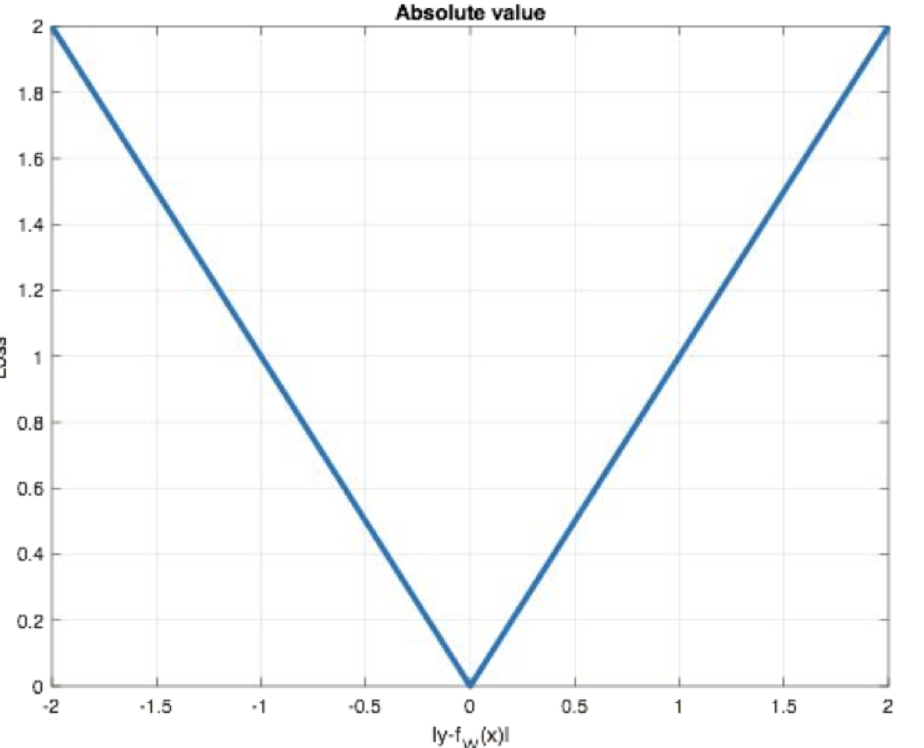
2. 回归任务：误差度量

MAE（L1 Loss）

平均绝对误差，对异常值不敏感。

y_true = torch.tensor([1.0, 2.0, 3.0])
y_pred = torch.tensor([2.0, 2.5, 5.0])loss = nn.L1Loss()
my_loss = loss(y_pred, y_true)
print('MAE loss:', my_loss)

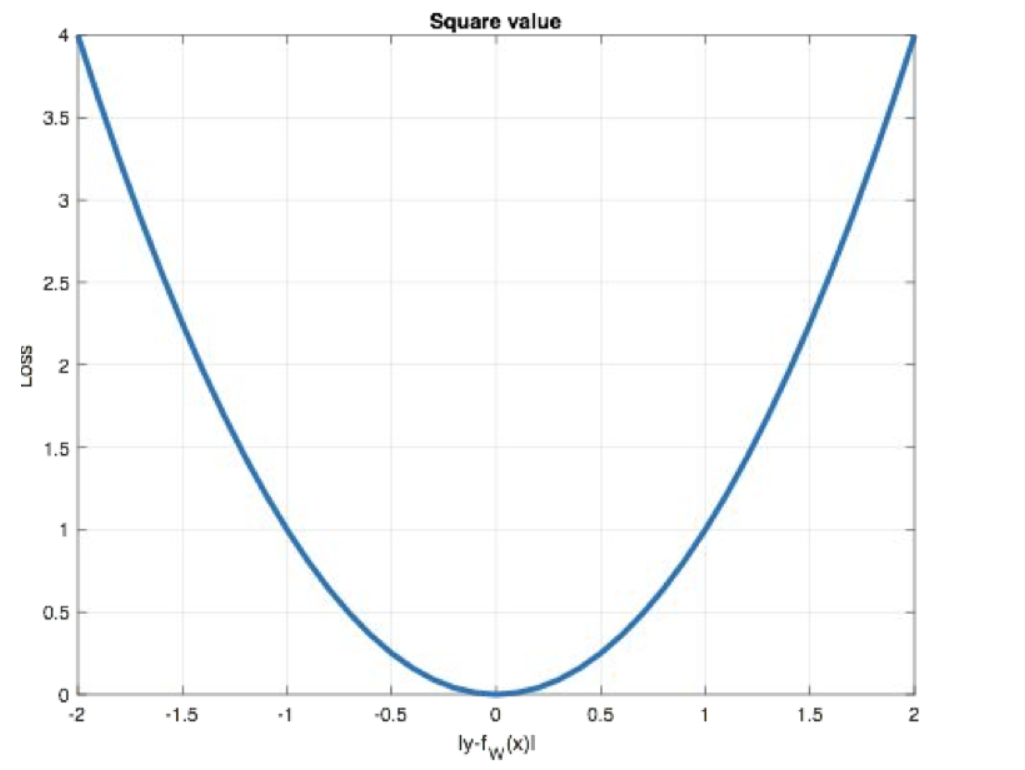
MSE（L2 Loss）

均方误差，对离群点敏感。

loss = nn.MSELoss()
my_loss = loss(y_pred, y_true)
print('MSE loss:', my_loss)

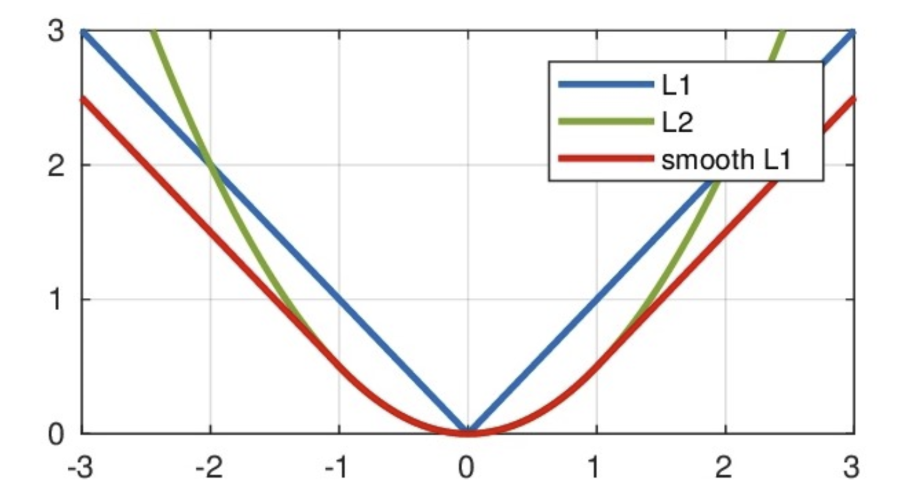
Smooth L1 Loss

结合 MAE 和 MSE 的优点，在误差小时像 MSE，大时像 MAE。

loss = nn.SmoothL1Loss()
my_loss = loss(y_pred, y_true)
print('Smooth L1 loss:', my_loss)

---

九、反向传播与梯度下降

1. 前向传播 vs 反向传播

• 前向传播：输入 → 输出，计算预测值。
• 反向传播：计算损失函数对每个参数的梯度，用于更新权重。

一次完整的训练迭代 = 前向传播 + 损失计算 + 反向传播

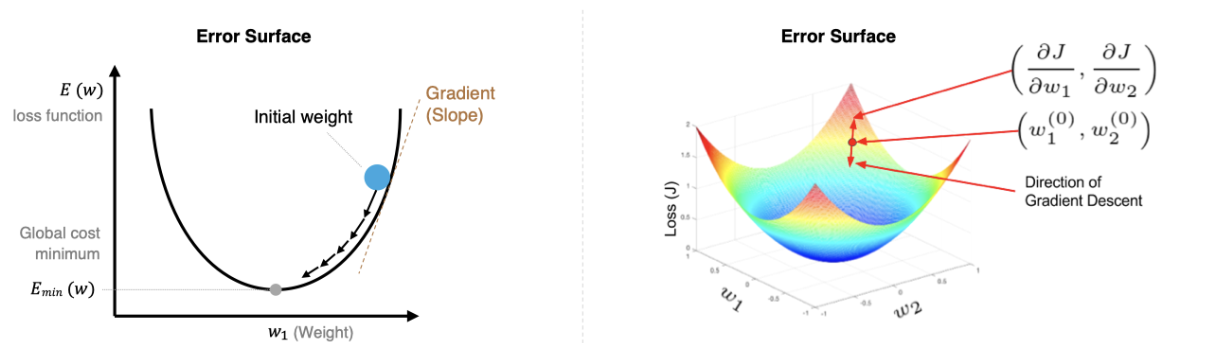
2. 梯度下降原理

梯度是函数增长最快的方向，负梯度方向就是下降最快的方向。

更新公式：
$$w\_t+1=w\_t-\eta \cdot \nabla \_wL$$
其中 $\eta$ 是学习率。

批量大小（Batch Size）的影响

类型	Batch Size	特点
BGD（批量梯度下降）	整个数据集	稳定但慢
SGD（随机梯度下降）	1	快但震荡
Mini-batch GD	小批量（如 32, 64, 256）	最常用，平衡速度与稳定性

---

十、优化算法进阶

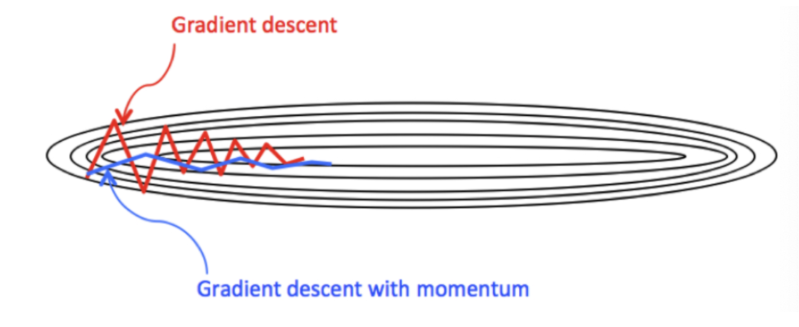
1. Momentum（动量法）

使用指数加权平均累积历史梯度，加速收敛，减少震荡。

optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)

2. Adam（自适应矩估计）

结合 Momentum 和 RMSProp，自适应学习率，NLP 和大模型中最常用。

optimizer = torch.optim.Adam([w], lr=0.01)

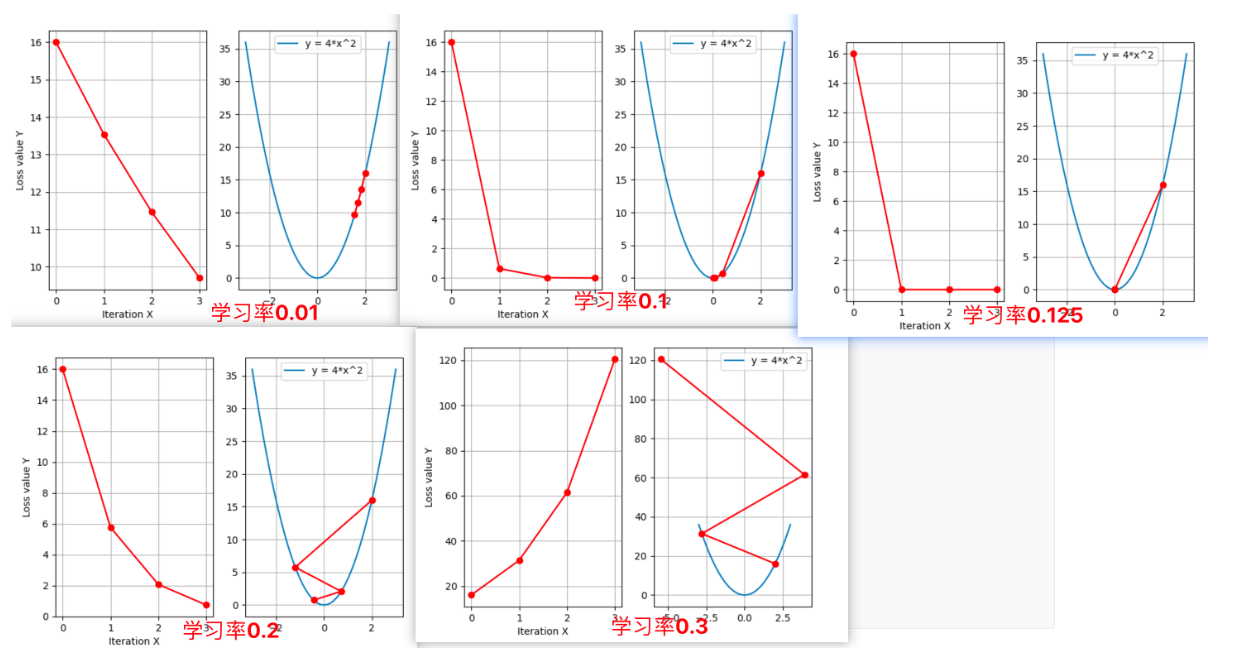
3. 学习率衰减策略

训练后期减小学习率，防止震荡。

• StepLR：每隔固定步数衰减
• MultiStepLR：在指定 epoch 衰减
• ExponentialLR：指数衰减

scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

---

总结

本文系统介绍了神经网络的核心概念：

• 前向传播：数据从输入到输出的流动过程
• 激活函数：引入非线性，提升表达能力（ReLU 为王）
• 参数初始化：决定训练成败的关键（优先选用 Kaiming/Xavier）
• 损失函数：分类用交叉熵，回归用 Smooth L1
• 优化算法：SGD + Momentum 或 Adam
• 学习率调度：防止后期震荡

---

参考资料：

• PyTorch 官方文档
• NumPy 广播机制