队列+宽搜(BFS)-662.二叉树最大宽度-力扣(LeetCode)
目录
一、题目解析
1、宽度定义为最左节点和最右的非空节点之间的长度
2、类比char的存储(一个首尾相连的环,127+1!=128 = -127),虽然int可能会溢出,但是所得的差,由题目保证的32位范围内,所以结果是不会溢出的
二、算法原理
解法1:直接统计nullptr的数目(这虽然是一个错误的解法,但仍有其价值)
解法2:利用数组存储二叉树,给节点编号
编号呢有两种,可以自行选择
宽度的保存
具体过程
三、代码示例
解法2:
看到最后,如果对您有所帮助,还请点赞、收藏和关注一键三连,在未来还会继续带来优秀的内容,感谢观看,我们下期再见!
一、题目解析
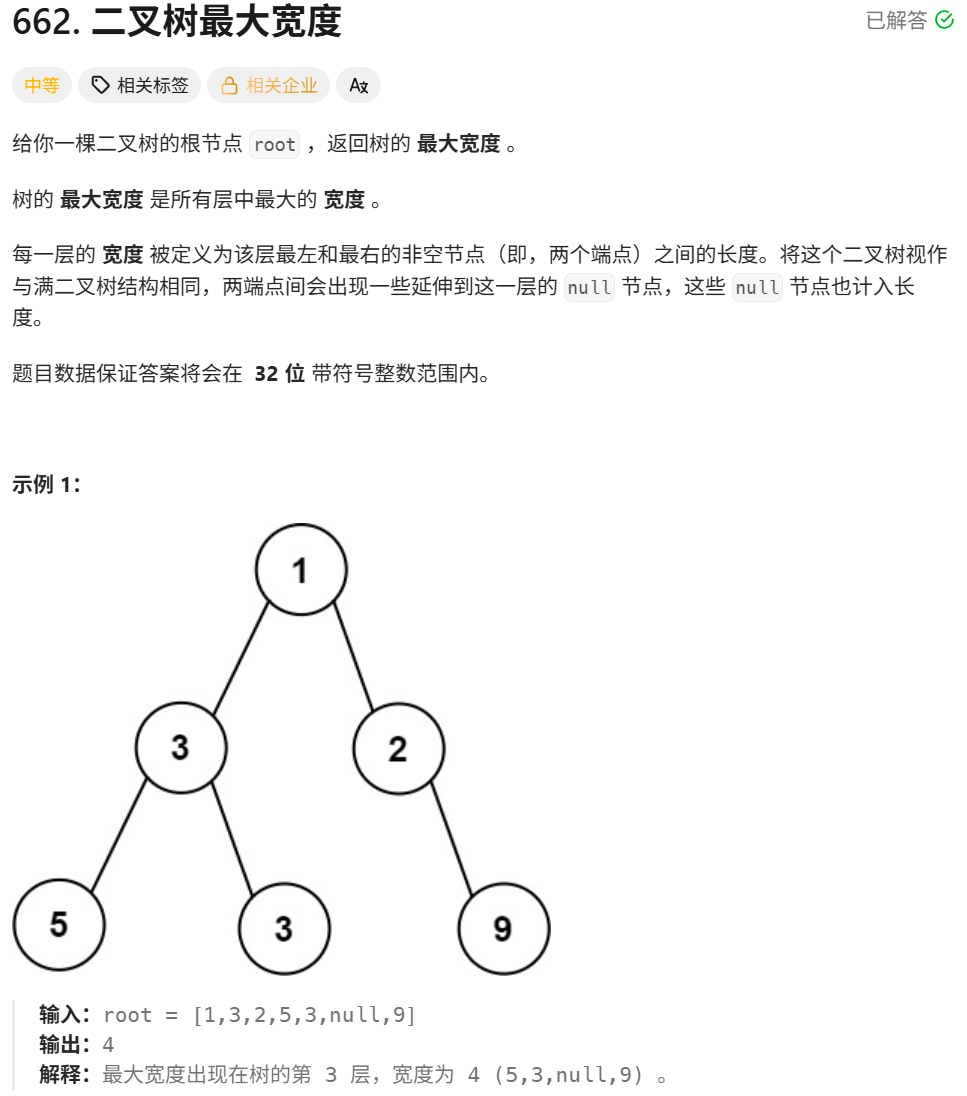
1、宽度定义为最左节点和最右的非空节点之间的长度
2、类比char的存储(一个首尾相连的环,127+1!=128 = -127),虽然int可能会溢出,但是所得的差,由题目保证的32位范围内,所以结果是不会溢出的
二、算法原理
解法1:直接统计nullptr的数目(这虽然是一个错误的解法,但仍有其价值)
在遇到第一个非空节点后,开始统计nullptr的数目,在遇到下一个非空节点时,返回结果
错误之处:
存在着某个测试样式,将3000个节点左右均分,所以此时最后一层的节点树大概有2^1497个这么多
但我们在学习二叉树的时候,简单模拟是通过数组实现的,可以通过给节点编号,将节点存储在数组中,所以便有了解法2
解法2:利用数组存储二叉树,给节点编号
之前的队列都是只存储节点的指针,但我们要利用编号进行宽度计算,所以queue中或者vector模拟应存储一个pair<TreeNode*,long>的类型的数据,为什么用long呢?当然是int编号溢出了
编号呢有两种,可以自行选择
1、root为0,左孩子为2*0+1,右孩子为2*0+2,其他节点也是如此
2、root为1,左孩子为2*1,右孩子为2*1+1,其他节点也是如此
宽度的保存
结合题目和 char存储的模型,我们知道了最后的结果是有效的,但是该如何保存这个宽度呢?通过unsigned int无符号整数存储这个宽度,但是为了方便得到最终的最大值,可以初始化为1(也可以处理只有根的情况)
具体过程
参考层序遍历,只不过中间有一些空节点需要处理
在对每一层遍历时,先统计队列中的元素个数,这个个数代表该层元素个数,也代表循环次数
我们first是TreeNode*,用于判断它的左右孩子是否入队(我这里选择是nullptr不入队),second是节点的编号,用于计算宽度
在层序遍历完后,取出队列对头(左端点)和队尾(右端点),计算宽度并且与上一次结果比较,如果比上次大则更新宽度,否则不更新
三、代码示例
解法2:
class Solution {
public:int widthOfBinaryTree(TreeNode* root){queue<pair<TreeNode*,int>> qti;unsigned int ret = 1;//特殊处理只有根if(root) qti.push({root,0});//入根while(qti.size()){int num = qti.size();pair<TreeNode*,long> tmp;//int会溢出while(num--)//执行每层个数次{tmp = qti.front();qti.pop();if(tmp.first->left) qti.push({tmp.first->left,2*(tmp.second)+1});//不入空if(tmp.first->right) qti.push({tmp.first->right,2*(tmp.second)+2});//通过编号计算宽度}if(qti.size())ret = ret>qti.back().second-qti.front().second+1 ? ret : qti.back().second-qti.front().second+1;//取对头和队尾做计算} return ret;}
};
