当前位置：首页 > news >正文

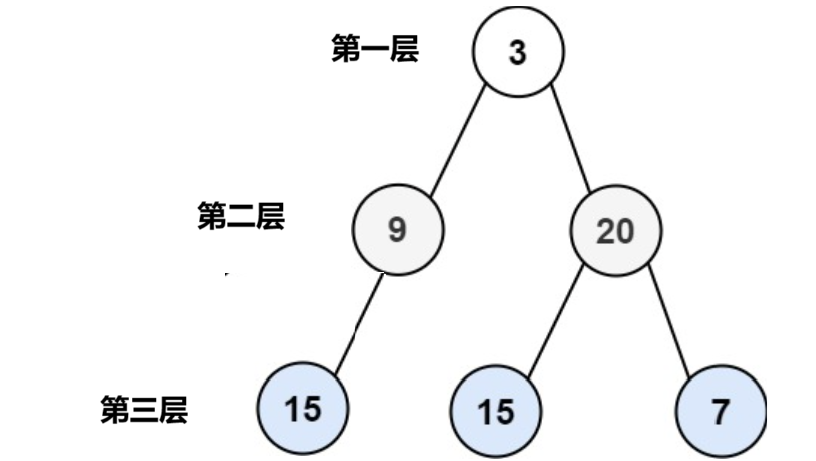
【数据结构OJ】BFS算法的可视化：二叉树“层序遍历”

news 2025/9/26 8:36:47

今天我们来分享一道关于二叉树层序遍历的OJ算法题

题目介绍：

1、核心定义

2、实现核心及思路

解题思路：

思路可视化：

代码实现：

代码测试：

题目介绍：

接口函数以及二叉树节点结构：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {}
};

题目来源：leetcode：107.二叉树的层序遍历II

1、核心定义

二叉树的层序遍历，又称广度优先遍历（BFS），是指从根节点开始，按“从上到下、从左到右”的顺序逐层访问树中所有节点，先遍历完第1层（根节点），再遍历第2层，以此类推，直到最后一层的所有节点都被访问。

2、实现核心及思路

二叉树层序遍历的本质就是 “先进先出” 的访问逻辑，队列是实现该逻辑给关键数据结构。

大概思路：我们可以将二叉树的节点的地址存入队列，同时，用一个level_k_size来记录每一层的节点个数，和一个数组 v 来存储每一层数据，然后利用" level_k_size-- " 来控制节点出队列的个数，保证每一层的节点都能够出尽，在节点出队列的同时将节点的val值插入数组v并将该节点不为空的孩子节点继续带入队列；这样利用 level_k_size每循环一次得到一层的数据，直到遍历完整个二叉树。

解题思路：

（1）通过题目介绍，我们知道函数最后需要返回vector<vector<int>>的二维数组，所以，我们先创建一个二维数组 vv。

（2）判断二叉树是否为空，即根结点root是否为nullptr。若为空则则不做处理，最后返回一个空的二维数组vv；不为空，则将根结点root入队列，同时 level_k_size记录节点个数为1。

（3）根据level_k_size来遍历已经入队列的节点。由于level_k_size记录的是对应一层的节点数，就可以用 level_k_size作为while循环的循环次数来遍历节点，利用队列的front接口函数获取队头的节点，将队头节点的val值插入到数组v（可以用vector创建数组），然后，将该节点不为空的孩子节点带入队列，同时，将队头节点出队列（pop）。

⭐️注意：a. 这里不能直接将节点直接出队列，防止节点被释放而找不到孩子节点。可以用node记下该节点，然后pop（删除队头节点）。

b. 每次出队头节点都要保证将其对应的不为空的左右孩子节点带入队列，保证在下一次遍历时，已经出队列的节点的下一层的所有节点都在队列中，便于准确更新level_k_size的值。

（4）遍历完一层的节点之后，将数组v中的数据插入（push_back）到二维数组vv，然后更新level_k_size的值，得到下一层节点的个数。

（5）当队列中再没有节点时，证明二叉树的所有节点已经都遍历完了，因为上一层节点的左右孩子节点都为空，即二叉树遍历完成。但是，题目要求我们从二叉树的叶子节点所在层开始向上遍历，所以，我们先将二维数组vv进行逆置处理（reverse），再返回即可。

思路可视化：

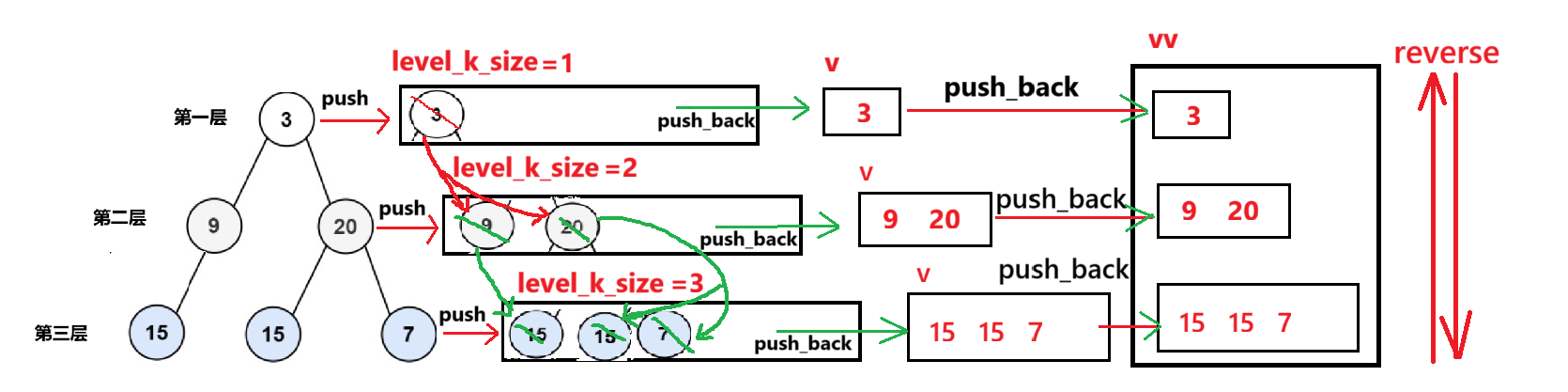
代码实现：

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {vector<vector<int>> vv;    // 创建二维数组int level_k_size=0;       if(root!=nullptr){_q.push(root);   // 插入根结点level_k_size=1;  // 记录节点个数}while(!_q.empty()){vector<int> v;  // 创建数组vwhile(level_k_size--)  // 遍历一层{TreeNode* node=_q.front(); //记下队头节点_q.pop();                  // 释放v.push_back(node->val);    // 将数据插入到vif(node->left)             // 带入左孩子节点{_q.push(node->left);}if(node->right)            // 带入右孩子节点{_q.push(node->right);}}vv.push_back(v);  // 将数组v的数据插入二维数组      level_k_size=_q.size(); // 更新level_k_size的值}reverse(vv.begin(),vv.end()); // 逆置return vv;}
private:queue<TreeNode*> _q; // 成员变量（队列）
};

代码测试：

int main()
{ solution s;// 创建一棵二叉树TreeNode node1(3);TreeNode node2(9);TreeNode node3(20);TreeNode node4(15);TreeNode node5(15);TreeNode node6(7);// 连接node1._left = &node2;node1._right = &node3;node2._left = &node4;node3._left = &node5;node3._right = &node6;vector<vector<int>> vv;vv = s.levelOrderTravelsal(&node1); // 调用函数for (int i = 0; i < 3; i++){for (int j = 0; j < vv[i].size(); j++){cout << vv[i][j] << " ";}cout << endl;}
}