当前位置：首页 > news >正文

P13013 GESP5级202506 编程T1--奖品兑换

news 2025/9/25 17:17:27

P13013 [GESP202506 五级] 奖品兑换

题目背景

为了保证只有时间复杂度正确的代码能够通过本题，时限下降为 400 毫秒。

题目描述

班主任给上课专心听讲、认真完成作业的同学们分别发放了若干张课堂优秀券和作业优秀券。同学们可以使用这两种券找班主任兑换奖品。具体来说，可以使用 $a$ 张课堂优秀券和 $b$ 张作业优秀券兑换一份奖品，或者使用 $b$ 张课堂优秀券和 $a$ 张作业优秀券兑换一份奖品。

现在小 A 有 $n$ 张课堂优秀券和 $m$ 张作业优秀券，他最多能兑换多少份奖品呢？

输入格式

第一行，两个正整数 $n, m$ ，分别表示小 A 持有的课堂优秀券和作业优秀券的数量。

第二行，两个正整数 $a, b$ ，表示兑换一份奖品所需的两种券的数量。

输出格式

输出共一行，一个整数，表示最多能兑换的奖品份数。

输入输出样例 #1

输入 #1

8 8
2 1

输出 #1

输入输出样例 #2

输入 #2

314159 2653589
27 1828

输出 #2

说明/提示

对于 $60%60\%$ 的测试点，保证 $\le a,b \le 100$ ， $\le n,m \le 500$ 。

对于所有测试点，保证 $\le a,b \le 10^4$ ， $\le n,m \le 10^9$ 。

Bilibili视频

先康康我的bilibili视频

(进度条不对劲)家人们出事啦！我用O(2^n)的递归方式，居然AC了n在10000以内的题目！

10分钟，很长的。
这个视频针对这道题给出了三种解法：递归、贪心、二分。
如果考试问你学到什么道理，直接抄上！
在这里插入图片描述

题目大意

给定四个正整数 $n$ , $m$ , $a$ , $b$ ,分别表示手里的课堂优秀券、手里的作业优秀券、一个奖品需要的课堂优秀券、一个奖品同时需要的作业优秀券（ $a$ , $b$ 可以随时交换，视频忘说了）

递归解法

假设递归函数为dfs，那么应该传入这些参数：i j cnt，表示剩余课堂优秀券、剩余作业优秀券、已获得奖品数量。
对于dfs(i,j,cnt)可以推出dfs(i-a,j-b,cnt+1)和dfs(i-b,j-a,cnt+1)，前提是够换奖品。
先别管超时，我们先写代码。

#include<bits/stdc++.h>
using namespace std;
int a,b,mx;
void dfs(int i,int j,int cnt)
{mx=max(mx,cnt);if(i>=a&&j>=b)dfs(i-a,j-b,cnt+1);if(i>=b&&j>=a)dfs(i-b,j-a,cnt+1);
}
int main()
{int n,m;cin>>n>>m>>a>>b;dfs(n,m,0);cout<<mx;return 0;
}

一号样例过
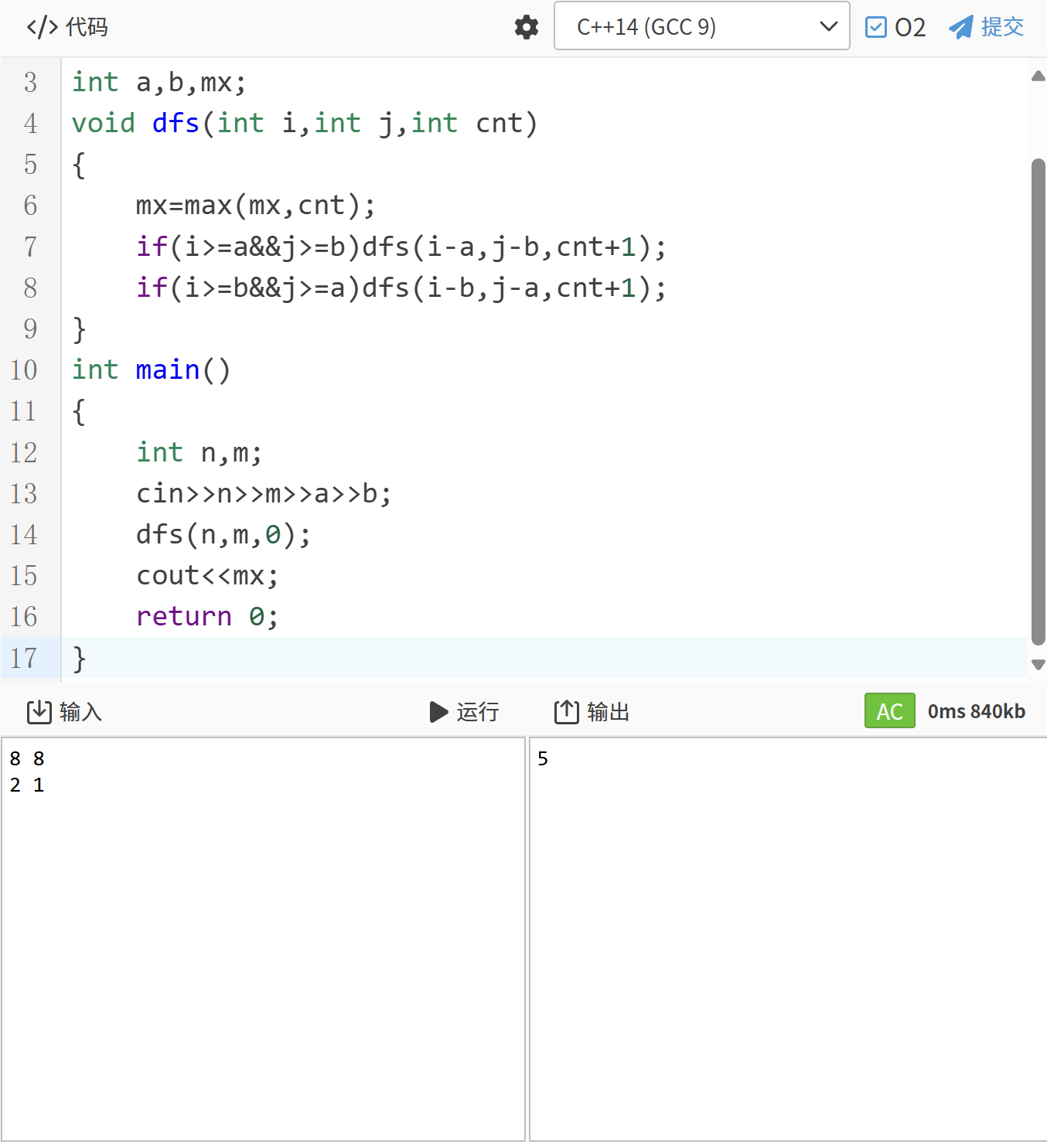
在这里插入图片描述
遇到二号就噶了

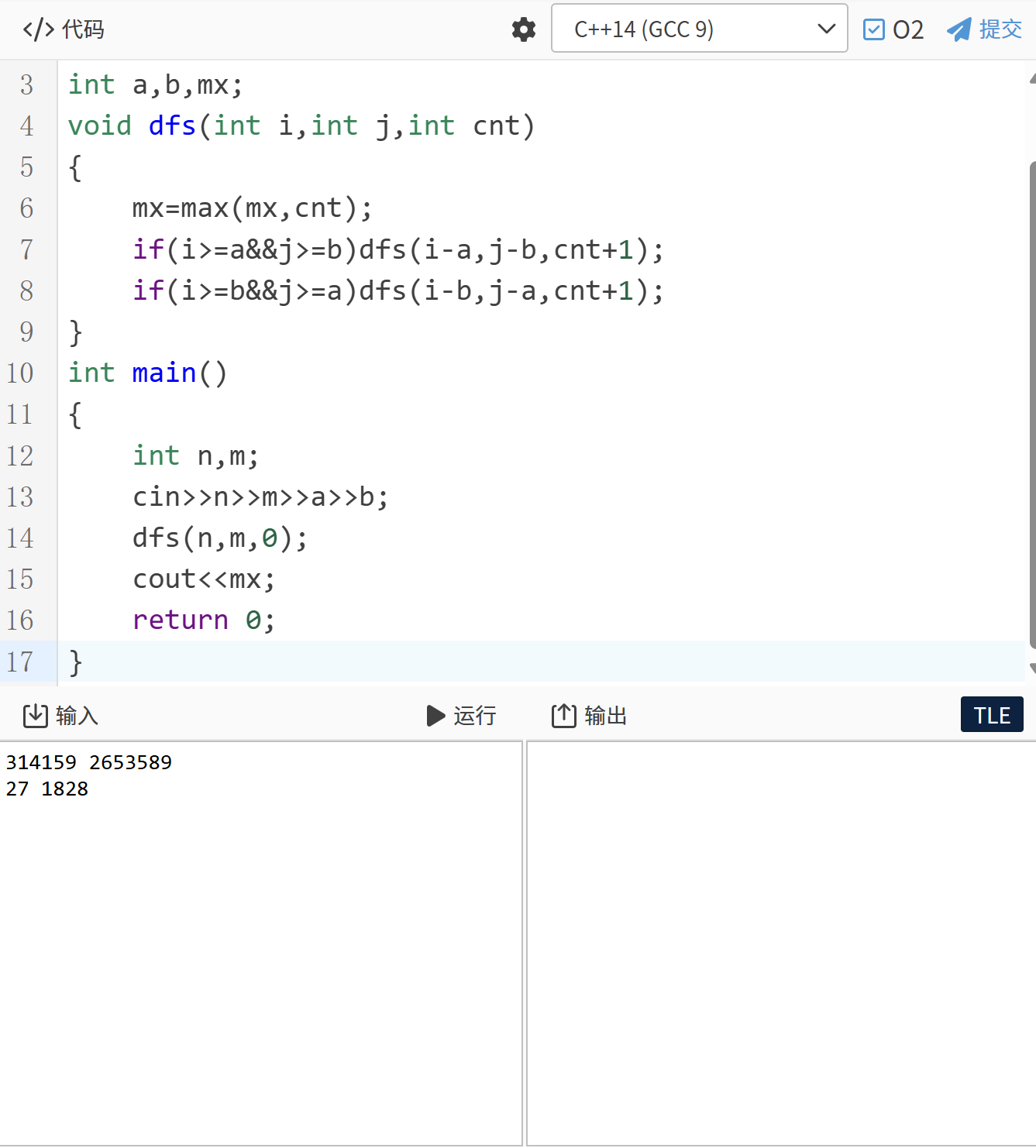
提交逝世

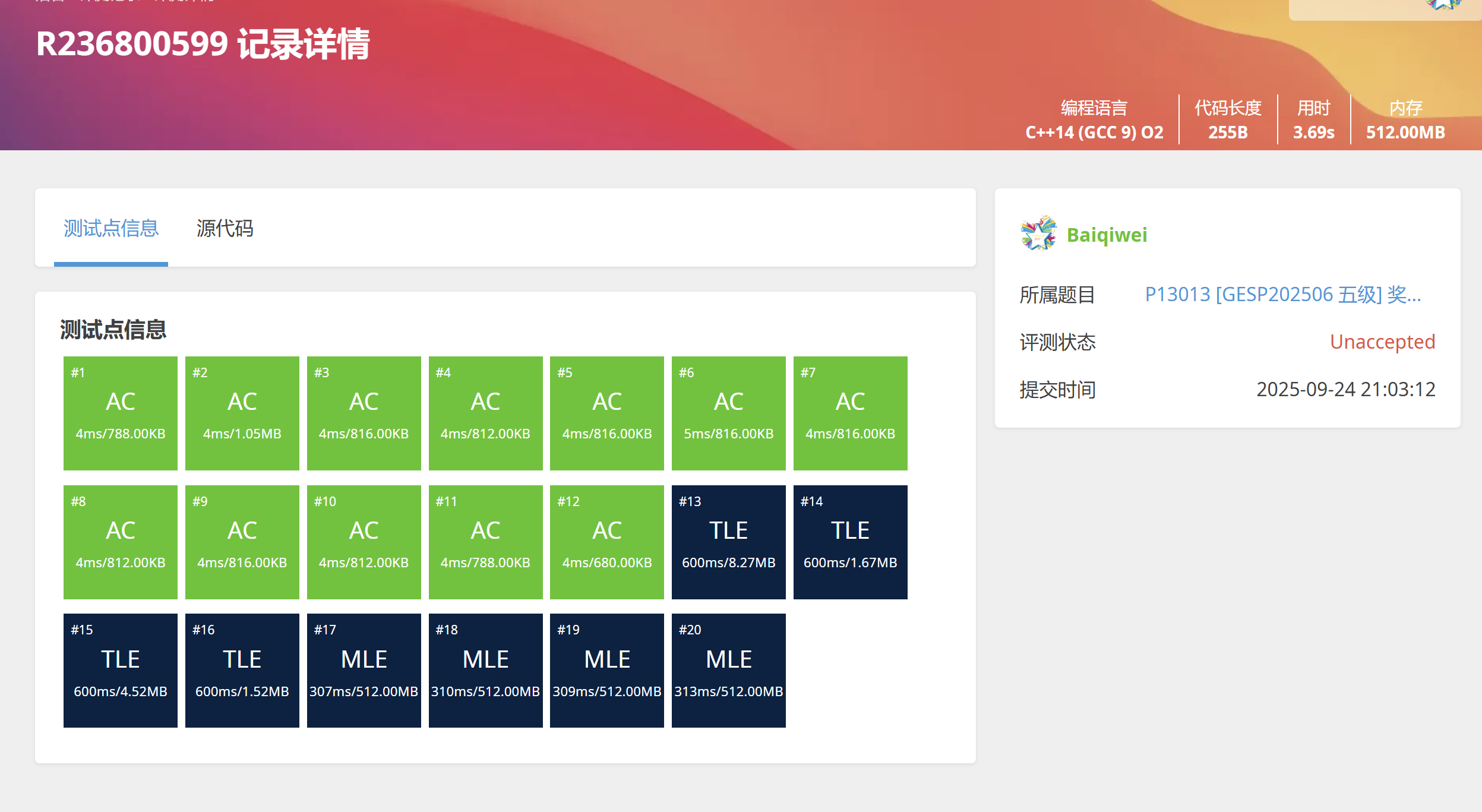
~~我怎么感觉二号样例有助于我们背圆周率呢~~
这里有12个AC，4个TLE，4个MLE，其中tle是超时，mle是超内存（超递归栈）

递归复杂度

每个递归函数引导两个子函数，差不多 $O(2^n)$ 吧？
空间应该就是 $O (n)$ 了，细致的说， $O(na+mb)O(\frac{n}{a}+\frac{m}{b})$ （并不准）

贪心

我们尽可能地让 $n, m$ 中的较大者去减 $a, b$ 中的较大者，较小者同理，这样分配对 $n, m$ 公平，可以多分点。
于是代码就"bang"出来了

#include<bits/stdc++.h>
using namespace std;
int main()
{int n,m,a,b,cnt=0;cin>>n>>m>>a>>b;while(n>=a&&m>=b||n>=b&&m>=a) //c++中，先算&&，再算||{if(n>=m) //n大，优先选n-max a,b{n-=max(a,b);m-=min(a,b);}else //m大，优先选m-max a,b{n-=min(a,b);m-=max(a,b);}cnt++;}cout<<cnt;return 0;
}

样例1、2全都能通过
在这里插入图片描述
然而提交时的你又双叒叕(you4 shuang1 ruo4 zhuo2)傻眼了

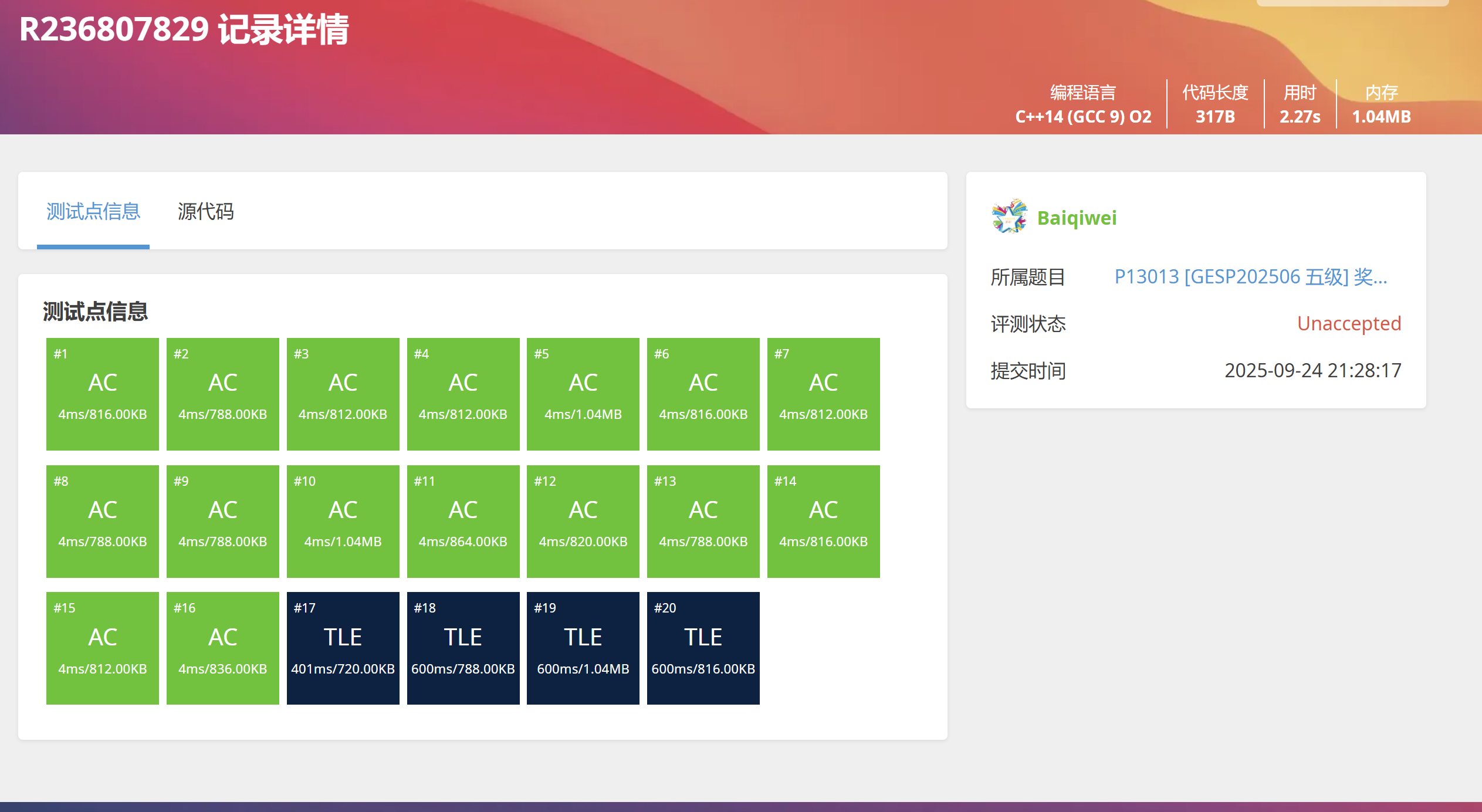
~~哇！第17个点正好超时1ms~~
就在你想放弃时，突然点到了展开算法标签。

二分！？我想试试。
有谁注意到了

二分AC版

我们假设最多兑换的奖品份数为 $x$ ，思考🤔如何判断 $x$ 是不是合法的奖品份数（小于等于标准答案）。
首先调整 $a < b$ 以便后期操作。
当 $n≥axn\ge ax$ 并且 $m≥axm\ge ax$ 时，必然兑换够用！其中第二种利用 $a$ 比 $b$ 小，尽量让后面的剩余资源空间大。
那么如果是两种方案混合来呢？
我们来看一句话：
“今有鸡兔同笼，上有三十四头，下有九十四足，问鸡兔各几何？”
我们一般用假设法来解决鸡兔同笼问题，设全都是什么，然后把一部分变成另一种，最后求出数量。
那么这道题也可以用假设法。
现在假设全都是 $a, b$ 类（ $a$ 课堂 $b$ 作业），要想改成 $b, a$ 类，就要多搞来 $b - a$ 个课堂优秀券。而 $n - a x$ 是剩下的课堂优秀券，因此 $⌊n−axb−a⌋\lfloor\frac{n-ax}{b-a}\rfloor$ 就是 $b, a$ 类的数量，同理。
假设全都是 $b, a$ 类，要想改成 $a, b$ 类，就要多搞来 $b - a$ 个作业优秀券。而 $m - a x$ 是剩下的作业优秀券（因为 $a, b$ 可以互换， $a$ 更小剩余的更大），因此 $⌊m−axb−a⌋\lfloor\frac{m-ax}{b-a}\rfloor$ 就是 $a, b$ 类的数量。
如果他们加起来小于 $x$ ，就说明 $x$ 太大了，因此可以把他们存进check函数，对于后面的二分答案有帮助。

bool check(int num)
{if(n<a*num || m<a*num)return false;int ab=(m-a*num)/(b-a),ba=(n-a*num)/(b-a);return ab+ba>=num;
}

因为二分经常写错，所以提一点
1 当check(mid)返回true，l=mid，因为合法， l不能加 $1$
2 当check(mid)返回false，r=mid-1，因为不合法，r必须减 $1$
3 mid=(l+r+1)/2，因为l=3 r=4时，(l+r)/2且check(3)=true时，mid会一直等于 $3$ ，l永远不变，也就超时了，(l+r+1)/2可以避免。
4 l<r是循环进入条件，如果有等于那么l和r会永久重合，TLE了。
知道这一点，没问题了，开始写Code吧！

AC Code

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b;
bool check(int num)
{if(n<a*num || m<a*num)return false; //基础资源分配int ab=(m-a*num)/(b-a),ba=(n-a*num)/(b-a); //a,b类b,a类转换return ab+ba>=num;
}
int main()
{cin>>n>>m>>a>>b;if(a>b)swap(a,b); //调整a和b大小if(a==b){cout<<min(n,m)/a;return 0;} //直接计算long long l=0,r=2e9;while(l<r){int mid=(l+r+1)/2;if(check(mid))l=mid; //合法else r=mid-1; //不合法}cout<<l;return 0;
}

目前这个代码是能通过样例的，l r必须开long long，mid可以不用。
在这里插入图片描述
…

孩子们！mid要开long long，想起那个WA时钢管掉落的声音了吗！
因为check里面对mid和其他变量进行了乘法，必须开long long！！！

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b;
bool check(int num)
{if(n<a*num || m<a*num)return false; //基础资源分配int ab=(m-a*num)/(b-a),ba=(n-a*num)/(b-a); //a,b类b,a类转换return ab+ba>=num;
}
int main()
{cin>>n>>m>>a>>b;if(a>b)swap(a,b); //调整a和b大小if(a==b){cout<<min(n,m)/a;return 0;} //直接计算long long l=0,r=2e9;while(l<r){long long mid=(l+r+1)/2;if(check(mid))l=mid; //合法else r=mid-1; //不合法}cout<<l;return 0;
}

样例不用说了肯定对了
（一种植物）
在这里插入图片描述
孩子们！check里面的num也要开long long！！！
~~（一个二分代码改了三次）~~

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b;
bool check(long long num)
{if(n<a*num || m<a*num)return false; //基础资源分配int ab=(m-a*num)/(b-a),ba=(n-a*num)/(b-a); //a,b类b,a类转换return ab+ba>=num;
}
int main()
{cin>>n>>m>>a>>b;if(a>b)swap(a,b); //调整a和b大小if(a==b){cout<<min(n,m)/a;return 0;} //直接计算long long l=0,r=2e9;while(l<r){long long mid=(l+r+1)/2;if(check(mid))l=mid; //合法else r=mid-1; //不合法}cout<<l;return 0;
}