讲一讲什么是重要性采样
重要性采样（Importance Sampling）是一种用于估计期望值的蒙特卡洛方法，尤其在目标分布难以直接采样的情况下非常有用。其核心思想是：通过从一个更容易采样的“建议分布”（proposal distribution）中采样，然后对样本进行加权，以无偏地估计目标分布下的期望。
一、重要性采样的基本原理
假设我们想计算某个函数 f(x) 在目标分布 p(x) 下的期望：
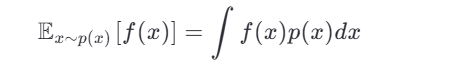
但直接从 p(x) 采样困难。于是我们引入一个容易采样的建议分布 q(x) （要求 q(x)>0 当 p(x)>0 ），则：
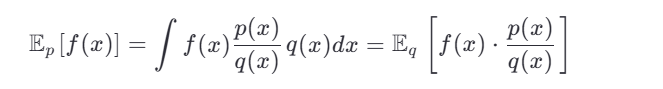
因此，我们可以从 q(x) 中采样 x1,...,xN ，然后用加权平均估计期望：
这些权重 wi 称为重要性权重。
注意：如果 p(x) 和 q(x) 差异太大，权重方差会很高，导致估计不稳定。因此选择好的 q(x) 很关键。
二、在大模型/NLP 面试中，重要性采样的应用场景
在大语言模型（LLM）和 NLP 领域，重要性采样常用于以下任务：
1. 语言模型评估（如 Perplexity 估计）
- 当测试集分布与训练分布不一致时，可用重要性采样校正。
- 例如：用一个较小的语言模型作为 q(x) ，估计大模型 p(x) 的 log-likelihood。
2. 强化学习中的策略梯度（如 PPO、A2C）
- 在 off-policy 学习中，用旧策略（behavior policy）采样，通过重要性采样权重调整为新策略（target policy）的期望。
- 权重为：πold(a∣s)πnew(a∣s)
3. 文本生成中的多样性控制
- 在 beam search 或 sampling 时，用重要性采样从近似分布（如 top-k、nucleus sampling）中采样，再加权估计真实分布下的指标。
4. 模型蒸馏或知识迁移
- 用教师模型的输出分布作为目标 p(x) ，学生模型或简单采样器作为 q(x) ，通过重要性采样估计教师模型的期望损失。
5. 罕见事件估计（如低概率但高影响的文本）
- 例如：评估模型对对抗样本或极端输入的鲁棒性，可设计 q(x) 更倾向于生成这类样本。
三、相关/改进方法（面试可提）
Self-Normalized Importance Sampling
当 p(x) 未归一化（如语言模型的 unnormalized logits），使用归一化权重：
这在 NLP 中很常见，因为语言模
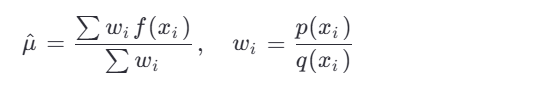型通常输出未归一化的分数。Adaptive Importance Sampling
动态调整 q(x) 使其更接近 p(x) ，例如通过迭代优化建议分布。Multiple Importance Sampling (MIS)
使用多个建议分布混合采样，降低方差。Stratified Sampling + Importance Sampling
分层采样后加权，提升估计效率。Doubly Robust Estimators（双重鲁棒估计）
结合重要性采样和回归模型，即使其中一个模型错误，估计仍可能无偏（常用于因果推断、推荐系统）。