【字符串算法集合】KMP EXKMP Manacher Trie 树 AC 自动机
按综合考虑排序,包括难度和逻辑顺序。
初学者看这一篇就能初步了解字符串专题要解决什么样的问题,以及怎么解决。
1.KMP
KMP (Knuth-Morris-Pratt) 算法是一种高效的字符串匹配算法。
当给出一个长串(长度为 n)一个短串(长度为 m),要你从长串中找短串,并输出起始位置。
朴素算法是 ,而 KMP 可以达到
。
前缀函数是整个 KMP 的核心(下文模式串就是短串):
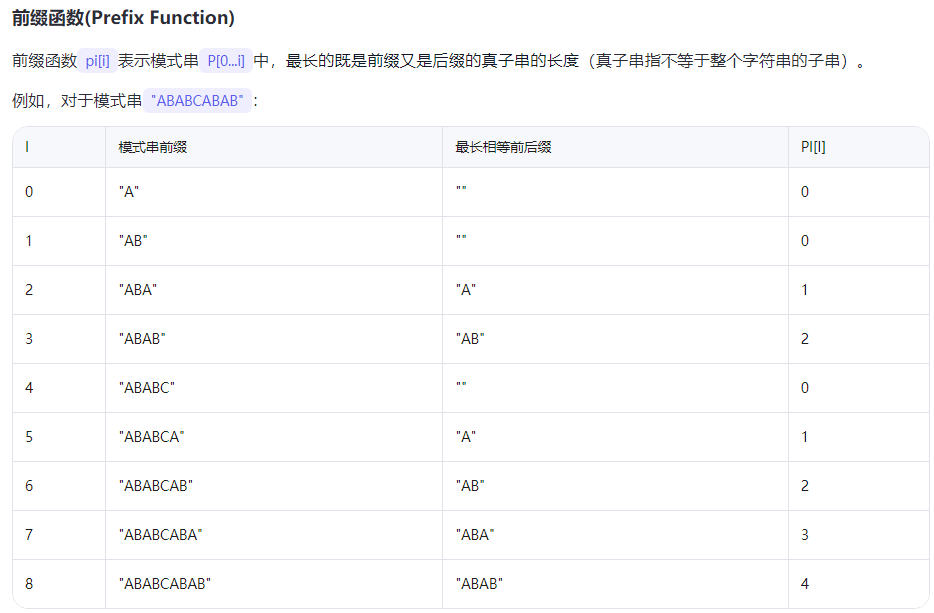
具体流程:
例如,当短串 ABABC 与长串匹配到第 5 个字符失败时:
我们已经匹配了 ABAB,
前缀函数告诉我们 ABAB 的最长相等前后缀是 AB (长度为 2),
所以我们可以将短串指针左移 2 位,让短串的前 2 个字符 AB 与长串中已经匹配的 AB
(实际上是之前匹配短串的第 3、4 个字符,现在对应短串的前两个字符)对齐。
例题:P3375 【模板】KMP - 洛谷 (luogu.com.cn)
(border 就是前缀函数。)
注释代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1e6 + 10;char sa[N], sb[N]; // 长短字符串
int p[N], ans[N]; // 前缀函数数组,和短串在长串出现的起始位置 int main () {ios::sync_with_stdio(false);cin.tie(0);cin >> sa + 1 >> sb + 1; // base-1 的读入 int lena = strlen(sa + 1);int lenb = strlen(sb + 1);memset(p, 0, sizeof(p)); // 清零 p 数组// 我们需要执行两次 kmp 操作,一次是短串自己的,一次是长短串匹配 // 短串自己的 for (int i = 2, j = p[i - 1]; i <= lenb; i++, j = p[i - 1]) { // i 从 2 开始,代表后缀开始的位置,j 从 0 开始,代表已和后缀匹配的前缀位置 - 1 // 为什么是 - 1?因为不匹配的话退回来很麻烦,不如直接匹配 i 和 j + 1 的位置 // 因为 j + 1 对应 i,所以 j 对应 i - 1,j = p[i - 1] while (j > 0 && sb[i] != sb[j + 1]) { // 如果不匹配,而且有位置可退 j = p[j]; // j 退回到当前 1 到 j 字串前后缀匹配的前缀结束位置// 假设 p[j] = 2,那么就代表着 1 到 1 + 2 - 1 和 j - 2 + 1 到 j 是相同的 // 而且 j - 2 + 1 到 j 这段位置和 i - 1 - 2 + 1 到 i - 1 是相同的// 这时如果 i 和 j + 1 不匹配,那么把 j = p[j],相当于把 1 到 1 + 2 - 1 对应 i - 1 - 2 + 1 到 i - 1// 接着往后匹配 }if (sb[i] == sb[j + 1]) { // 相等,代表 1 到 j + 1 和 i - (j + 1) + 1 到 i 是匹配的,赶紧赋值前缀函数 p[i] = j + 1;}}int len = 0;for (int i = 1, j = 0; i <= lena; i ++) {// i 从 1 开始,长串和短串匹配的起始位置,j 从 0 开始,代表短串已经和长串匹配的字符个数 while (j > 0 && sa[i] != sb[j + 1]) { // 匹配不成功 j = p[j]; // j 退回到短串 1 到 j 字串前后缀匹配的前缀结束位置// 之前保证短串 1 到 j 和长串 i - j 到 i - 1 是相同的 // 所以 j - p[j] + 1 到 j 这段位置和 i - p[j] 到 i - 1 也是相同的// 现在 i 和 j + 1 不匹配// 那就把短串的 1 到 1 + p[j] - 1 对应长串的 i - p[j] 到 i - 1// 接着往后匹配,看看 i 等不等于 1 + p[j]}if (sa[i] == sb[j + 1]) { // 能匹配 j ++;}if (j == lenb) { // 匹配完短串了 len ++;ans[len] = i - lenb + 1; // 匹配开始位置// 下一次循环肯定 i 和 j + 1 不匹配,j 就倒退回短串的前缀函数那了,继续找下一个可以匹配短串的地方 }}for (int i = 1; i <= len; i ++) {cout << ans[i] << "\n";}for (int i = 1; i <= lenb; i ++) {cout << p[i] << " ";}cout << "\n";return 0;
}昆明篇应用场景:
(1)判断单一字符串是否出现
(2)字符串出现周期
(3)和前后缀有关的问题都可以试试
2.EXKMP
又名扩展 KMP / exKMP(Z 函数),也是给你一个长串和一个短串。
求长串的每个后缀与短串的最长公共前缀 (LCP,Longest Common Prefix)。
(长串的每个后缀与长串自己的最长公共前缀也就是 z 函数)
时间复杂度也是要求 。
例题:P5410 【模板】扩展 KMP/exKMP(Z 函数) - 洛谷 (luogu.com.cn)
直接看代码吧:
#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 2e7 + 10;
char sa[N], sb[N];
LL z[N], p[N]; // z: sb 的 Z 函数数组, p: EXKMP 数组
int lena, lenb;// 计算文本串 sb 的 Z 函数
// z[i] 表示 sb[i..lenb]与 sb[1..lenb] 的最长公共前缀长度(LCP)
void get_z() {memset(z, 0, sizeof(z)); z[1] = lenb; // 特殊情况:sb[1..lenb]与自身的 LCP 就是整个字符串长度// 初始化最右匹配区间 [l, r]// 这区间就是 sb[l..r] = sb[1..r - l + 1]// l、r: 当前已知最右匹配区间的左端点和右端点for (int i = 2, l = 0, r = 0; i <= lenb; i ++) {// i 从 2 开始,代表后缀开始的位置,l = r = 0,一开始并没有区间 // 如果 i 在当前最右匹配区间 [l, r] 内if (i <= r) {z[i] = min(z[i - l + 1], 1ll * (r - i + 1));// 根据定义 1 到 r - l + 1 和 l 到 r 是相等的// 所以 i - l + 1 到 r - l + 1 和 i 到 r 是相等的// 因此以 i - l + 1 为标准,最大 LCP 最多就可以取 r - i + 1// 但是如果这个 r - i + 1 比 z[i - l + 1] 还要大的话,那当然取不了// 反之 r - i + 1 比 z[i - l + 1] 小,那也不能取大的// 因为只有 i - l + 1 到 r - l + 1 是相等的 }// 从 z[i] 开始尝试扩展匹配// 检查 sb[1 + z[i]] 和 sb[i + z[i]] 是否相等while (1 + z[i] <= lenb && i + z[i] <= lenb && sb[1 + z[i]] == sb[i + z[i]]) {z[i] ++; // 匹配成功,LCP 长度 + 1}// 如果匹配后右边界超过当前最右匹配区间,则更新区间if (i + z[i] - 1 > r) {l = i; // 新区间的左端点r = i + z[i] - 1; // 新区间的右端点}}
}// 计算 EXKMP 数组 p
// p[i] 表示 sa 从第 i 个字符开始的后缀与 sb 的 LCP
// ***和上面的函数几乎一模一样
void get_p() {// 初始化最右匹配区间 [l, r]// 这区间就是 sa[l..r] = sb[1..r - l + 1]memset(p, 0, sizeof(p));for (int i = 1, l = 0, r = 0; i <= lena; i++) {// i 从 1 开始,长串和短串匹配的起始位置// 如果 i 在当前最右匹配区间 [l, r] 内if (i <= r) {p[i] = min(z[i - l + 1], 1ll * (r - i + 1));}while (1 + p[i] <= lenb && i + p[i] <= lena && sb[1 + p[i]] == sa[i + p[i]]) {p[i] ++; // 匹配成功,LCP长度 + 1}if (i + p[i] - 1 > r) {l = i; // 新区间的左端点r = i + p[i] - 1; // 新区间的右端点}}
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> sa + 1 >> sb + 1;lena = strlen(sa + 1);lenb = strlen(sb + 1);get_z();get_p();LL ansa = 0, ansb = 0;for (int i = 1; i <= lenb; i ++) {ansa ^= (1ll * i) * (z[i] + 1);}for (int i = 1; i <= lena; i ++) {ansb ^= (1ll * i) * (p[i] + 1);}cout << ansa << "\n" << ansb << "\n";return 0;
}恶心昆明篇应用场景:
(1)求两个字符串的最长公共子串。
(2)字符串周期性分析。
(3)判断一个字符串是否为另一个字符串的循环节。
3.Manacher
马拉车算法(Manacher's Algorithm)是由 Glenn K. Manacher 在1975 年,
提出的一种高效解决最长回文子串问题的算法。
具体就是给你一个字符串 S,找出 S 中的最长回文子串。
朴素算法时间复杂度是 ,而马拉车可以做到
。
例题:P3805 【模板】manacher - 洛谷 (luogu.com.cn)
也是直接看代码吧:
#include<bits/stdc++.h>
using namespace std;const int N = 11e6 + 10; char s[2 * N], ss[N];
int d[2 * N], n;
// d[i]: 表示以 i 为中心的最长回文串向两边扩展的长度(包含中心点)
// 例如:对于字符串 "#a#b#a#",d[4] = 4(以 'b' 为中心的回文 "#a#b#a#")void get_d() {// 开头结尾添加边界字符防止越界s[0] = '$'; s[2 * n + 1] = '#'; // 在原始字符串的每个字符间插入'#',统一处理奇偶回文// 例如:"abc" -> "$#a#b#c#"// "abcd" -> "$#a#b#c#d#" // 这样大家的长度都是奇数了 (不包括 0 的边界) for (int i = 1; i <= n; i ++) {s[2 * i - 1] = '#'; s[2 * i] = ss[i]; } n = 2 * n + 1;memset(d, 0, sizeof(d));d[1] = 1; // 初始化第一个有效位置(索引 1)的回文半径// l、r:当前已知最右回文边界的左端点和右端点 // 这个最右回文 [l, r] 就是一个右端点在最右边的回文字串,中心点是 (l + r) / 2 // [l, r] 构成一个"盒子",用于加速后续计算for (int i = 2, l = 1, r = 1; i <= n; i ++) {// 如果 i 在当前最右回文边界内,"盒内加速"if (i <= r) {/*r - i + L 是 i 关于当前回文中心 (l + r) / 2 的对称点d[r - i + L] 是对称点的回文半径,因为整个 [l, r] 据回文中心对称,所以可以直接用 r - i + 1 是 i 到右边界 r 的距离取两者最小值作为 d[i] 的初始值(就是差不多 EXKMP 那样) 那么为什么不取 i 到回文中心的值一起做最小值呢? 因为两边对称,所以 i 的回文半径 d[i] 是可以越过回文中心的 */d[i] = min(d[r + l - i], r - i + 1);}// "盒外暴力" while (s[i - d[i]] == s[i + d[i]]) {d[i] ++; // 扩展成功,回文半径 + 1}if (i + d[i] - 1 > r) {l = i - d[i] + 1; // 新盒子的左边界r = i + d[i] - 1; // 新盒子的右边界}}
}int main() {ios::sync_with_stdio(false); cin.tie(0); cin >> ss + 1; n = strlen(ss + 1);get_d(); // 找出最长回文子串的长度int ans = 0;for (int i = 1; i <= n; i ++) { // 原串 "aba" -> 预处理串 "#a#b#a#"// d[4] = 4(以 'b' 为中心),原串回文长度 = 4 - 1 = 3// 严谨的来说,如果 d[i] 是偶数,那么回文半径一定长这样:#&#&#i(i 是实义字符) // 实义字符的个数为:(d[i] / 2) * 2 - 1,直接 - 1 就好 // 如果 d[i] 是奇数,那么回文半径一定长这样:#&#&i (i 是 #) // 实义字符的个数为:(d[i] / 2) * 2 - 1,也是直接 - 1 就好 ans = max(d[i] - 1, ans);}cout << ans << "\n"; return 0;
}
买辆车应用场景:
(1)寻找最长回文子串
(2)回文子串计数
(3)回文前缀/后缀分析
(4)字符串回文性质研究
4.Trie 树
先去看例题:P5755 [NOI2000] 单词查找树 - 洛谷 (luogu.com.cn)
简单来说就是从很多个串建成的树上找一些串的前缀。
单词查找树(Trie Tree),也称为前缀树(Prefix Tree)或字典树。
是一种特殊的树形数据结构,专门用于高效存储和检索字符串集合,时间复杂度 。
(N 是串的数量,M 是每个串的最大长度)
它的名字 "Trie" 来自 "retrieval"(检索),发音为 "try"。
代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1 << 16;
char s[110];
int id; // 当前已分配的节点 ID 计数器
int ch[N][26]; // ch[i][j] 表示节点i通过字母 ('A' + j) 到达的子节点// 将字符串插入Trie树
void ins(char *s) {int p = 0; // 从根节点(ID为 0)开始// 遍历字符串的每个字符for (int i = 0; s[i]; i++) {int j = s[i] - 'A'; // 将字符转换为 0-25 的索引(输入都是大写字母)// 如果当前节点 p 没有通过字符 s[i] 的边if (ch[p][j] == 0) {ch[p][j] = ++id; // 新建新节点 ID,并建立连接}p = ch[p][j]; // 移动到下一个节点}
}int main() {ios::sync_with_stdio(false); cin.tie(0); id = 0; // 初始化节点 ID 计数器(根节点 ID 为 0,不计入)memset(ch, 0, sizeof(ch)); // 初始化 Trie 树,所有连接置为 0(表示不存在)while (cin >> s) {ins(s); // 将每个字符串插入 Trie 树}// id 是从 1 开始计数的最后一个节点 ID// 总节点数 = id(已分配的非根节点数)+ 1(根节点)cout << id + 1 << "\n";return 0;
}塔日鹅应用场景:
(1)多个字符串求和前缀有关的问题
练习:P10470 前缀统计 - 洛谷 (luogu.com.cn)
代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1e6 + 10;
char s[N];
int ch[N][30], id;
int ed[N];void ins(char *s) {int p = 0;for (int i = 0; s[i]; i ++) {int j = s[i] - 'a';if (!ch[p][j]) {id ++;ch[p][j] = id;}p = ch[p][j];}ed[p] ++;
}int query(char *s) {int p = 0, sum = 0;for (int i = 0; s[i]; i ++) {int j = s[i] - 'a';if (!ch[p][j]) {return sum;}p = ch[p][j];sum += ed[p];}return sum;
}int main () {ios::sync_with_stdio(false);cin.tie(0);int n, m;cin >> n >> m;id = 0;memset (ch, 0, sizeof(ch));memset(ed, 0, sizeof(ed));for (int i = 1; i <= n; i ++) {cin >> s;ins(s);}for (int i = 1; i <= m; i ++) {cin >> s;cout << query(s) << "\n";}return 0;
} 5.AC 自动机
AC 自动机(Aho - Corasick 自动机)是一种用于多模式匹配的高效算法。
该算法由 Alfred V. Aho 和 Margaret J. Corasick 提出,主要用于解决多关键词同时匹配的问题。
例题:P5357 【模板】AC 自动机 - 洛谷 (luogu.com.cn)
简单来说就是从长串找很多个短串有没有出现,以及出现了几次。
(其实不一定要是从长串中找,从一堆串中找也行)
时间复杂度为 ,
其中 L 是所有短串的总长度,N 是整个 tire 树的总结点数,M 是长串长度。
整体的思路类似在 tire 树上的 KMP,也有一个功能相似的前缀数组。
(以下是 pre 数组的举例,比如 pre[3] = 1,强烈建议结合代码注释食用)
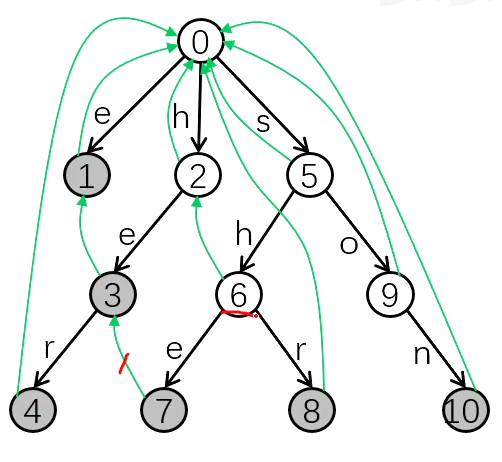
代码:
#include<bits/stdc++.h>
using namespace std;const int N = 1e6 + 10, M = 2e6 + 10;
char s[M];
int id, ch[N][26];
int ed[N], pre[N], sum[N];
// ed[i]:第 i 个短串的结束节点
// pre[i]:指向(根节点开始, i 节点结尾的字串)的后缀的节点,初始化为 0(指向根节点)
// sum[i]:统计节点 i 在文本串中被访问的次数vector<int> G[N]; // 用于构建失败指针(pre)树的邻接表// 插入短串到 Trie 树中(和前文 4.tire 一样就不过多介绍)
void ins(char* s, int x) {int p = 0;for (int i = 0; s[i]; i ++) {int j = s[i] - 'a';if (!ch[p][j]) {id ++;ch[p][j] = id;}p = ch[p][j];}ed[x] = p; // 记录第 x 个短串的结束节点
}// 建 AC 自动机的失败指针(pre)
void build() {queue<int> Q; // BFS 遍历 Trie树for (int i = 0; i < 26; i ++) if(ch[0][i]) {Q.push(ch[0][i]); // 将根节点的所有直接子节点入队(第一层的点) }while (!Q.empty()) {int x = Q.front(); Q.pop();for (int i = 0; i < 26; i ++) { // 遍历所有可能的字符int &y = ch[x][i]; // 引用,就相当于 y 和 ch[x][i] 绑定了,一个变另一个跟着变 if (y == 0) {y = ch[pre[x]][i]; // 如果 ch[x][i] 没有字符,那就到 x 的后缀的对应节点看看,说不定它有 }else {pre[y] = ch[pre[x]][i]; // y 的后缀就是 ch[x 的后缀][i] Q.push(y); // 将 y 入队}}}
}// 在 AC自动机上查询长串
void query(char* s) {int p = 0; for (int i = 0; s[i]; i ++) { // 遍历长串的每个字符p = ch[p][s[i]-'a']; sum[p] ++; // 记录该节点被访问的次数}
}// 遍历 pre 指针树,统计每个短串的出现次数
// 这里的每个节点是 pre[i] --> i 这样连边
// 可以看那张图上的绿箭头反着来
// 因为 pre[i] 是 i 的后缀
// 所以如果 i 节点被长串经过,那就可以累加数量到 pre[i](父节点)
// 因为 pre[i] 也一定被长串包含,而最后遍历加 sum 的时候只会加短串的结尾的节点
void dfs(int x) {// 遍历 x 的所有子节点(在 pre 指针树中)for(auto y: G[x]) {dfs(y); sum[x] += sum[y]; // 将子节点的匹配次数累加到父节点}
}int main() {ios::sync_with_stdio(false);cin.tie(0);int n; cin >> n;id = 0; memset(ch, 0, sizeof(ch));for (int i = 1; i <= n; i ++) {cin >> s;ins(s, i); }memset(pre, 0, sizeof(pre));memset(sum, 0, sizeof(sum));build(); // 构建 AC 自动机cin >> s; // 读长串query(s); // 在 AC 自动机上滚长串// 构建失败指针(pre)树for (int i = 1; i <= id; i++) {G[pre[i]].push_back(i);}dfs(0);for (int i = 1; i <= n; i ++) {cout << sum[ed[i]] << "\n";}return 0;
}交流电自动机应用场景:
(1)找很多个串有没有在一棵 trie 树中出现过
