一、移动零,复写零,快乐数
一.移动零
1.题目及题目分析:
题目:
https://leetcode.cn/problems/move-zeroes/

题目分析:
首先要明确,题目要求“就地”对数组进行操作,不能创建新数组然后把结果复制到这个新数组里。
然后这个问题属于明显的“数组划分”或“数组分块”问题,这类问题通常使用“双指针法”
“数组划分”/“数组分块”问题:

2.算法详解——双指针法
双指针法,不一定是要使用指针,也可以用数组下标来充当指针。
定义两个“指针”:cur(current:现在的)、dest( destination:目的地)
cur:从左往右扫描数组、遍历数组
dest:表示已处理区间内,非零元素的最后一个位置


由cur和dest就把数组分成了三个区间:
[0,dest]:都是非0的数
[dest+1,cur-1]:都是0
[cur,n-1]:未处理的部分
3.代码
class Solution {public void moveZeroes(int[] nums) {int cur=0;int dest=-1;int len=nums.length;while(cur<len){if(nums[cur]!=0){dest++;int temp=nums[cur];nums[cur]=nums[dest];nums[dest]=temp;}cur++;}}
}
二、复写零
1.题目及题目分析:
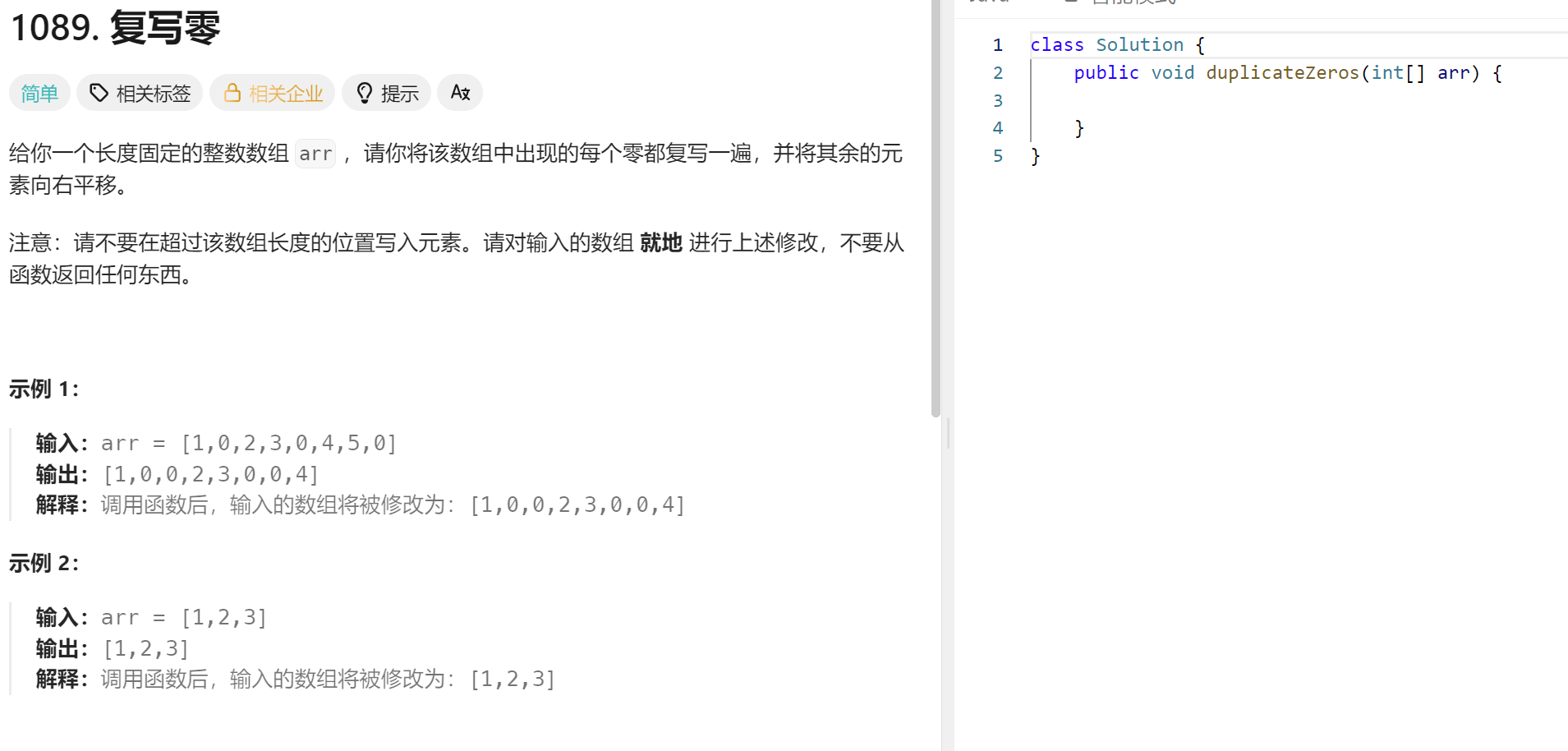
题目:https://leetcode.cn/problems/duplicate-zeros/description/
题目分析:

这个题目也可以先考虑一下双指针法
2.算法详解——双指针法
按照前面那种那种双指针法: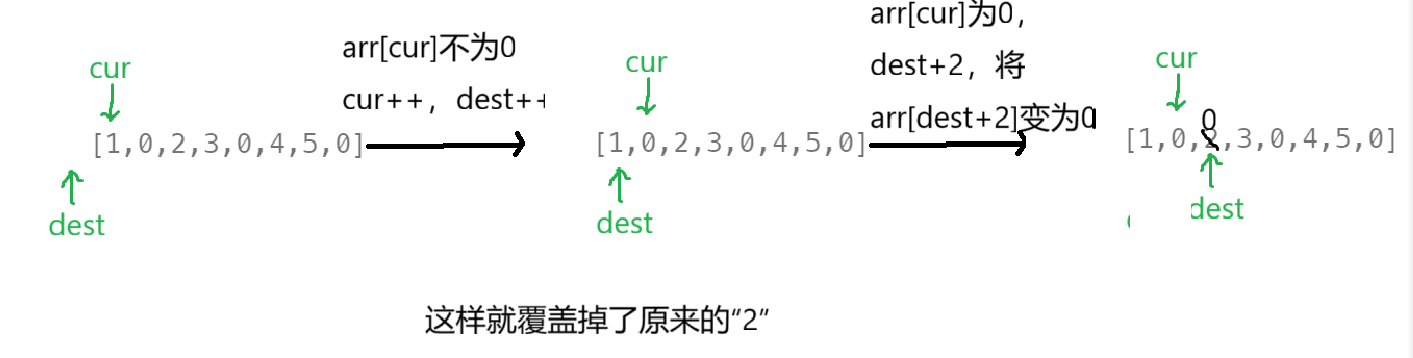
显然不行,当这个时候,就可以尝试:先“异地操作”(即先拿一个新数组辅助思考),得到解决方案后,再把这个方案优化成“就地操作”
异地操作:
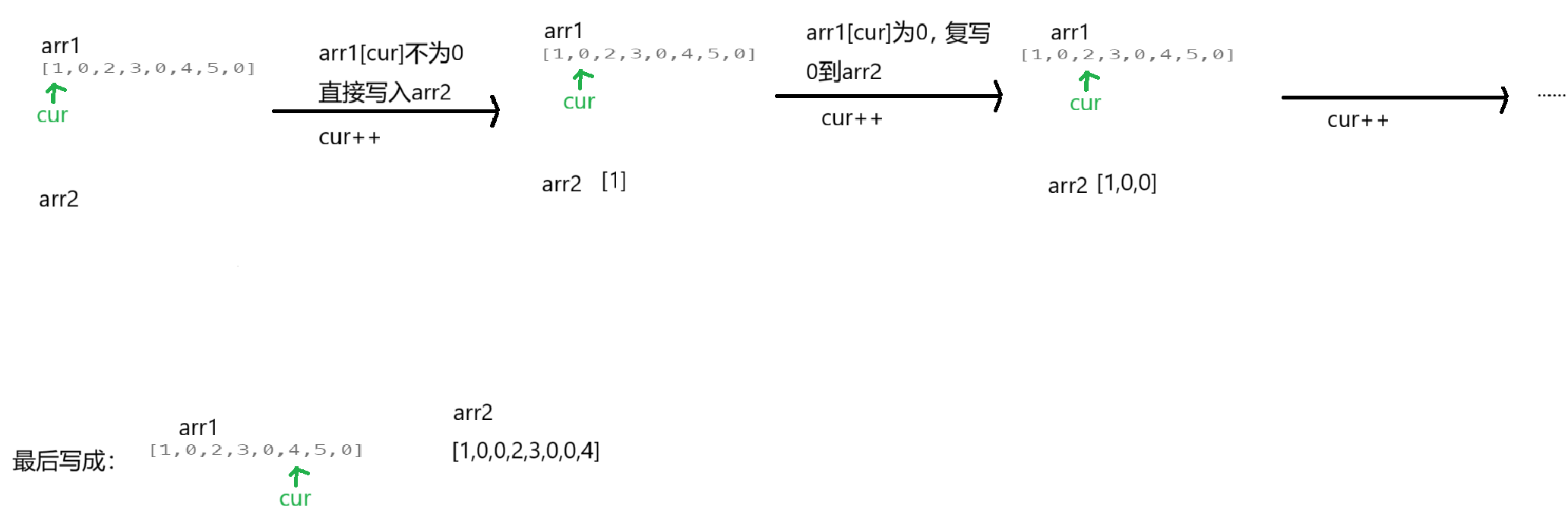
总结异地操作,转化为就地操作:
因为cur和dest从前往后会覆盖掉原来的元素,所以我们试试从后往前。
根据异地操作,我们可以先找到最后一个要写入arr2的数,让cur指向这个数的下标,dest从n-1位置开始。
然后从后往前进行复写,arr1[cur]!=0时,arr1[dest]=arr1[cur],cur--,dest--。
arr1[cur]==0时,dest要复写两次。
那么如何找到最后一个要写入arr2的数呢?
也是使用双指针

还有一个边界情况:如[1,0,2,3,0,4],这个数组最后要复写的数为0

所以这个时候,要让arr1[n-1]==0,并且cur-=1,dest--=2
3.代码
class Solution {public void duplicateZeros(int[] arr) {int cur=0;int dest=-1;int len=arr.length;while(cur<len){if(arr[cur]==0){dest+=2;}else{dest+=1;}if(dest>=len-1){break;}cur++;}//处理边界情况if(dest==len){arr[len-1]=0;cur--;dest-=2;}//从后往前复写while(cur>=0){if(arr[cur]!=0){arr[dest--]=arr[cur--];}else{arr[dest--]=0;arr[dest--]=0;cur--;}}//需理解这个错在哪:// int cur=0;// int dest=-1;// int len=arr.length;// while(dest<len){// if(arr[cur]==0){// dest+=2;// }else{// dest+=1;// }// cur++;// }// //处理特殊情况// if(dest==len){// arr[len-1]=0;// cur--;// dest-=2;// }// //从后往前复写// while(cur>=0){// if(arr[cur]!=0){// arr[dest]=arr[cur];// dest--;// }else{// arr[dest--]=0;// arr[dest--]=0;// }// cur--;// }}
}
三、快乐数
1.题目及题目分析:
https://leetcode.cn/problems/happy-number/description/

可以用“鸽巢原理”来证明为什么“重复这个过程可以直到这个数变为 1,或者无限循环但始终变不到 1”,这里不再赘述
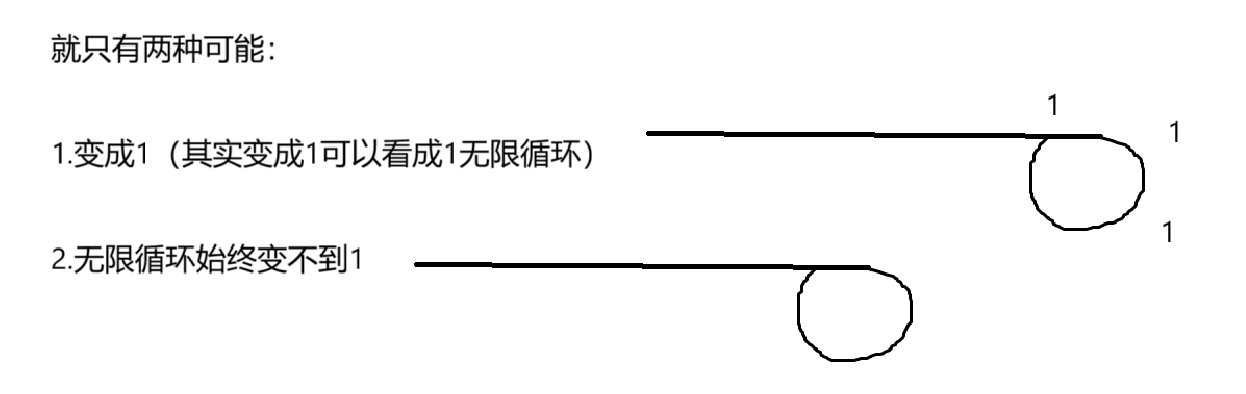
其实这里和“判断链表是否有环”问题很像,只是我们这里不是判断是否有环,因为已经确定是有环的,我们这里要判断的是:它的环里面是不是全是1,全是1则为快乐数
所以相似的,可以用“快慢双指针”法来解决这个问题
2.算法详解——快慢双指针法
和前面“双指针法”一样,“快慢双指针法”中的“指针”只是一类代称,不一定要是真的指针。
那么这个题如何定义快慢指针fast和slow:

解法为:1.定义快慢指针
2.慢指针每次向后移动一步,快指针每次向后移动两步
3.判断相遇时的值,为1则为快乐数,为其他则不是快乐数
3.代码
class Solution {//返回n这个数每一位的平方和public int bitSum(int n){int sum=0;while(n!=0){int t=n%10;sum+=t*t;n=n/10;}return sum;}public boolean isHappy(int n) {int slow=n;int fast=bitSum(n);while(slow!=fast){slow=bitSum(slow);fast=bitSum(bitSum(fast));}return slow==1;/*不能随便给,因为下面循环slow=n%10+slow中slow、fast初始值必须为0,所以下面循环用do while//先随便给slow、fast一个不相同的值,让他俩进入循环int slow=0;int fast=1;*//*int slow=0;int fast=0;do{while(n>0){slow=n%10*n%10+slow;n=n/10;}int j=slow;while(j>0){fast=j%10*j%10+fast;//这里error “+fast”fast越加越大j=j/10;}n=slow;}while(fast!=slow);if(fast==1){return true;}return false;*/}
}