Diffusion 模型解读

0. 前言

以前总用GAN，但是现在最新的都是Diffusion model，GAN只关注骗过判别器，模型在学习中可能会走捷径，无法控制，训练起来非常难。

DALL·E 2 就是用扩散模型做的。

扩散模型的鼎鼎大名相比所有人都听过，我是在VLA中接触到了这个东西，但是这个东西21年就非常火热了，直到今天还有很多人在研究，现在来详细看一看。

diffusion对动作生成友好，但是对指令的跟随不是很好–来自自变量

本文参考自：【【大白话01】一文理清 Diffusion Model 扩散模型 | 原理图解+公式推导】 https://www.bilibili.com/video/BV1xih7ecEMb/?share_source=copy_web&vd_source=b803c42182cb2250e40705156605fca1

1. 什么是 Diffusion Model

Denoising Diffusion Probabilistic Models

首先是前向扩散过程，一张原始图片经过T次加噪，得到一张杂乱无章的噪声图，原始论文加了2000次

是否有一种反向过程，能够把噪声图逐步去噪还原回图像。

什么是加噪？每次加一个01分布的高斯噪声

对于反向过程其实就是训练出一个神经网络，它可以预测出噪声，然后$x_t$时间步的信息减去模型预测出的噪声，就得到$x_{t-1}$时间步的图片，这就是去噪的一个过程。

1.1 前向扩散过程

在前向扩散过程的两个时间步之间加噪时，不是直接 前一步的+高斯分布=新一步的 。

而是有两个系数，通过线性组合来实现递增加噪的过程：

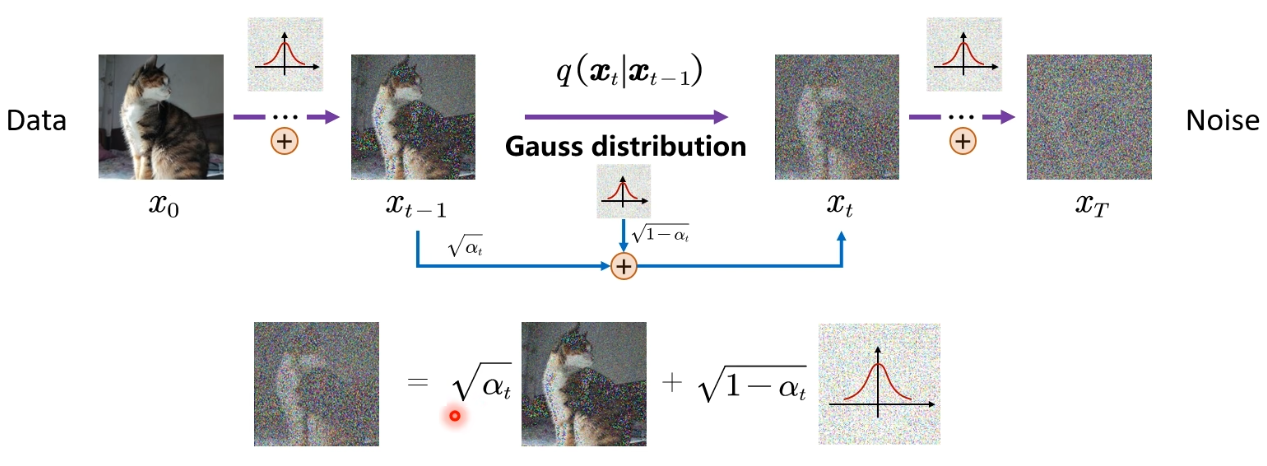
新生成的$x_t$的图是满足高斯分布的，经过数学推导可以知道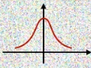：是01正态分布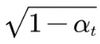，就是标准差，前面的就是均值。

写成数学表达式的样子就是：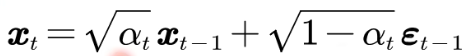

我们再用概率分布去组织一下$x_{t-1}$到$x_t$的过程，就得到了：

那么我们再把$x_t$的图片作为signal信号，高斯分布作为noise噪声，这就可以反映出信噪比。

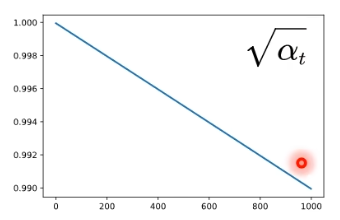
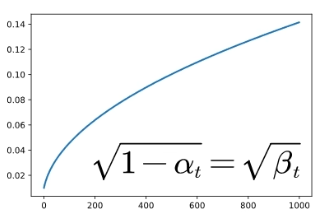
随着时间步的增加，均值越来越小，说明原始信号的幅度按比例缩放，相当于信息占比越来越少；标准差表示噪声强度，${\alpha }_t$越来越小，1-${\alpha }_t$就越来越大，随着时间步增加，加的噪声越来越多，数据越模糊。

因为刚开始一个原图的话，稍微加点噪声，变化就挺多了，后面噪声多了之后，得越加越多，不然体现不出变化。

上面是相邻两步的一个加噪过程，我们来看一下怎么 扩展到$x_0$到$x_t$

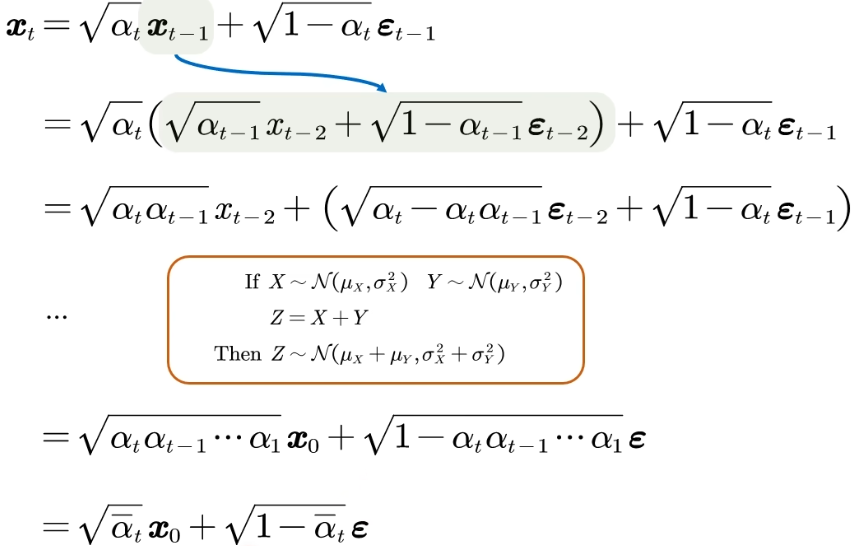
根据第一个式子可以看出：$x_t$只与$x_{t-1}$相关，展开之后就得到第二个式子，根据定理得知后面那个式子的两个高斯分布可以合并（各自平方后就满足定理，再相加后整体开根号），合并之后还是高斯分布，那么层层递归就可以得到最后的式子。

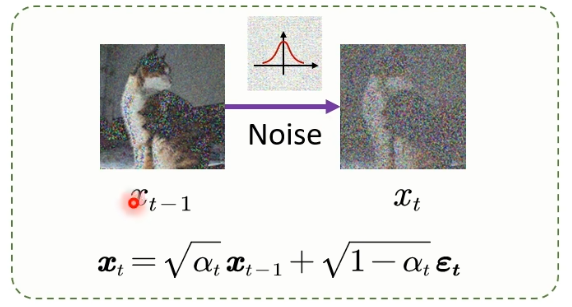
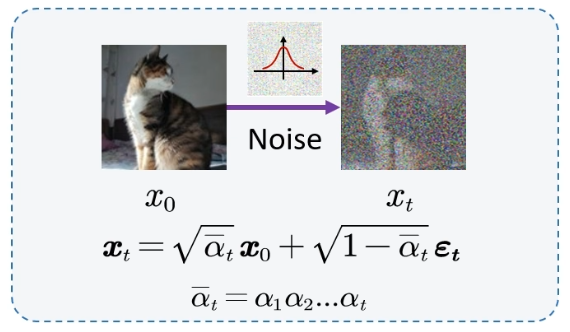
这样我们就得到了整个前向过程加噪的加噪过程，我们可以一步跳跃式的加噪到任意t时间步。

为什么要这样呢？因为我们的反向过程只需要最后的加好的噪声图，不关注前面的每一个时间步做的事情，所以从 $x_0$ 直接推导到 $x_t$ 就特别方便了。

这个就是diffusion中的第一个最核心的公式，代码中是一定会用到的。

1.2 反向扩散过程

现在能加噪了，但是我们的目的是去噪。

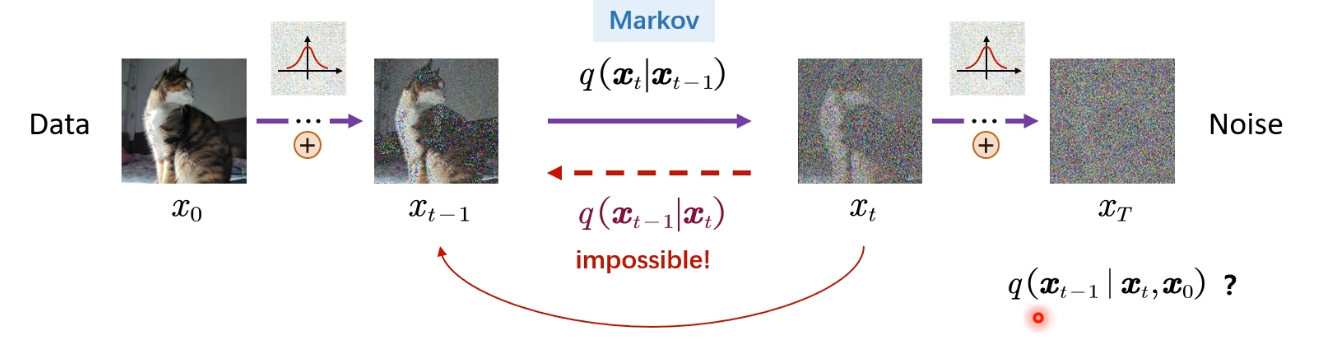
当我们有一堆随机噪点，需要逐步还原成不带噪音。上一步加噪我们可以从头一步加到尾，去噪确实做不到这个过程，只能一步步去噪。但是其实这个一步步去噪是很难做的，为什么呢？

因为反向过程时，我们只知道一个纯噪声，让它变换回原本的图像是非常难的，常规方法做不到，所以需要用神经网络了。

我们可以定义一个模型，让它去符合高斯分布。我们已知 $x_T$ 的分布，要求 $x_T-1$ 的分布，已知后一时刻，求前一时刻，通过贝叶斯公式：

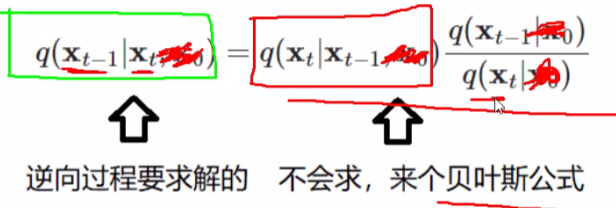
其中，这个是我们之前求出来的公式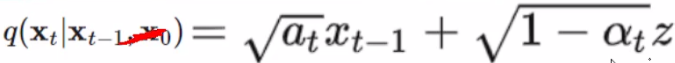：，那么$q(x_{t-1})$ 和 $q(x_t)$ 怎么求呢？别忘了，我们在前向加噪时，是可以通过求任意时刻的 $x_t$ 的，所以有$x_0$就行，于是这个公式会在后面加上$x_0$ ：

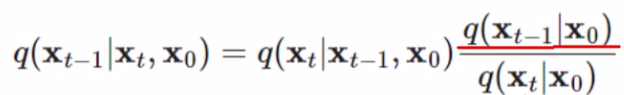
本质就是通过贝叶斯公式进行一个转换，往前推一步。把上面公式的每一子式都展开：

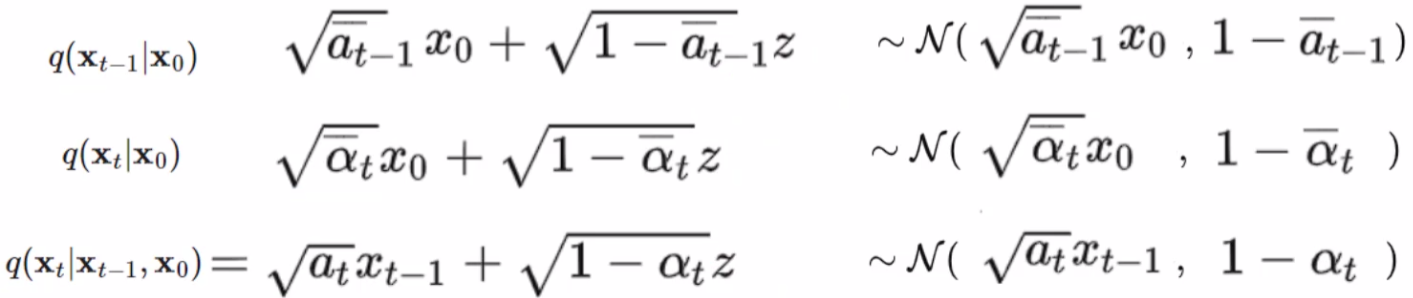
可以概括为以下内容：

正比关系：$f(x;\mu ,{\sigma }^2)\propto exp(-1/2\ast (x-\mu {)}^2/{\sigma }^2)$

z 是一个正态分布，乘上一个数，加上一个数，其实还是符合正态分布的，只是改变了均值和标准差，每个子式都是如此。$N()$括号里的第一项是均值，第二项是标准差，每一个子式按照标准正态分布展开：

我们可以仔细观察一下，以e为底的指数函数乘法相当于加，除法相当于减。第一项对应$q(x_t|x_{t-1},x_0)$，第二项$q(x_{t-1}|x_0)$，第三项$q(x_t|x_0)$。我们要求的东西就符合这样一个分布。

接下来就是化简，把平方展开，合并同类项：

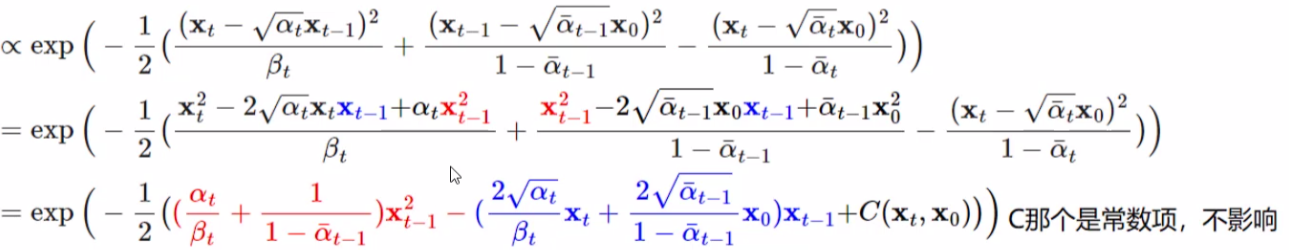
我们要求的是 $x_t$ 和 $x_{t-1}$ 的关系，我们只关心 $x_{t-1}$ 和谁有关系，所以上面合并同类项时就把$x_t-1$提取出来了。前一时刻也符合这种分布，所以可以一一对应：

这样和正态分布正比关系一对应，就得到 $x_{t-1}$ 分布的均值和方差了，$x_{t-1}$ 对应 $x$：
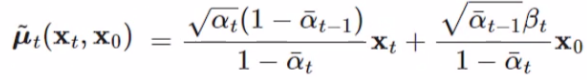，这个就是求出来的均值结果。

我们这个公式中还有 $x_0$，但是这个东西是我们最后要求的东西，这个东西是未知的，注意，我们在加噪时的公式是已知$x_0$，求$x_t$，那我们反过来就可以用$x_t$替换一下这个$x_0$，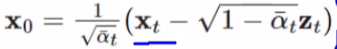
替换完成后的最终结果就变成了：

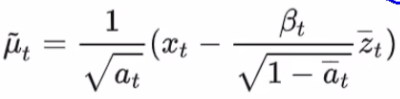
现在我们的均值只与$x_t$有关，也就是说我们已知$x_t$，就可以求出前一时刻 $x_{t-1}$ 分布的均值和方差，也就知道了它的分布，这个原始版本中方差是固定值，现在我们也把均值求出来了。这个$z_t$是个啥？这个是加噪时的噪音。

我们现在只知道$x_t$，这个时候的噪音又不知道，怎么办呢？训练一个模型，预测这个噪音是多少，但是损失需要的这个真实值怎么得到呢？这个标注怎么做呢?我们在前向加噪时就需要保存这些加噪的噪声，前向的过程其实就是提供这个标签的一个过程，反向去噪时就用这个标签拟合去噪。

这些相关论文里都是用Unet这种结构去做的，可能是编码和解码看的比较舒服，可能预测这个噪声不需要很复杂的网络结构。当然，训练阶段需要前向提供数据，训练好之后使用就可以了，每一步去噪时，输入是一直变的，所以都需要这个unet做一个去噪噪声的预测，当然unet的参数是不变的。

1.3 总结

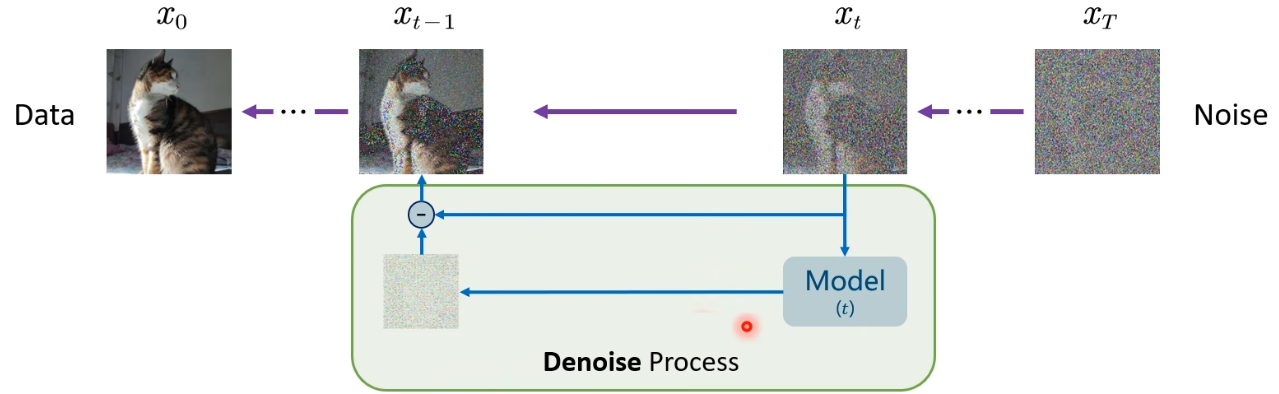
训练阶段就是训练一个预测噪声的模型，用模型预测出的噪声去拟合真实的噪声，算个损失，梯度下降更新参数，至于为什么要传t，是因为我们在加噪的时候，噪声是越加越大的，模型需要知道这个时间的影响。如下图：

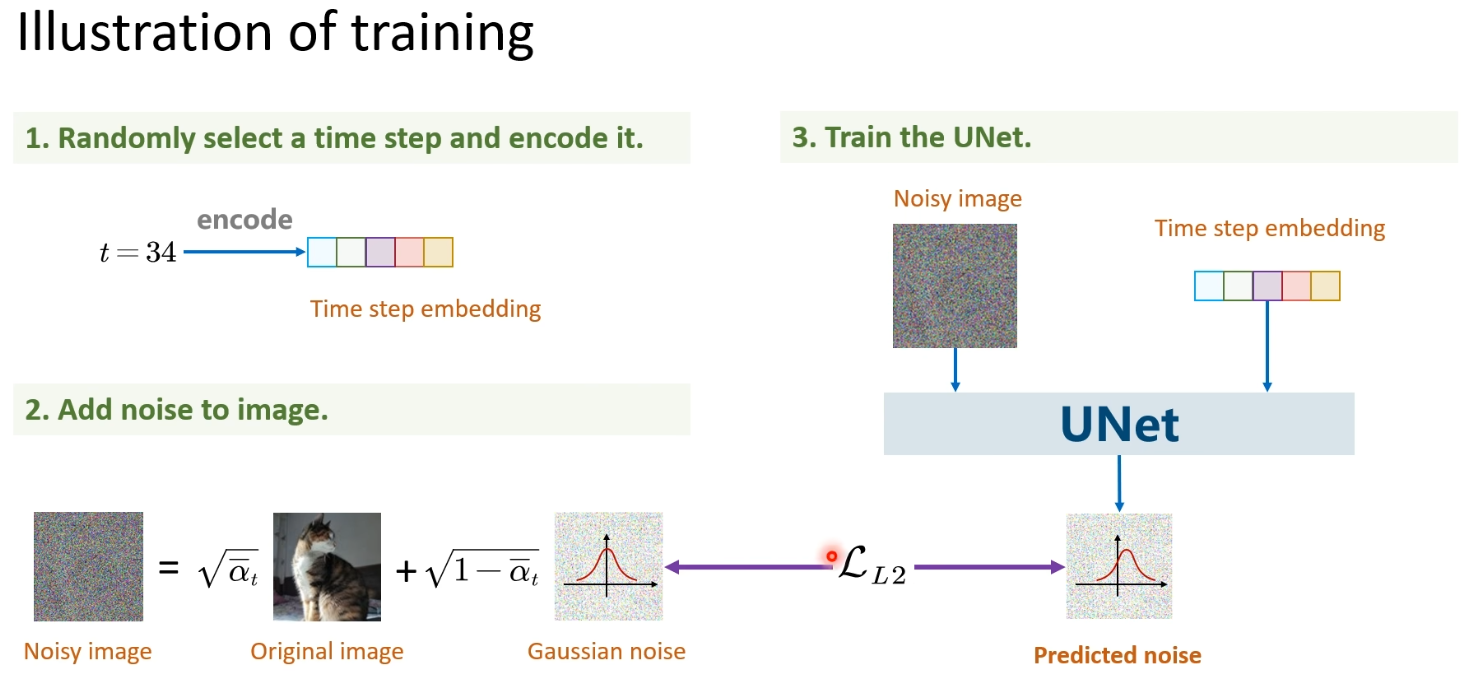
sampling 就是for循环一步一步去噪， $x_{t-1}$ 只与 $x_t$有关，用训练阶段训练出的模型，通过输入$x_t$的图像，t，预测出噪声，然后乘上系数，实现去噪。如下图：