2025研究生数学建模通用神经网络处理器下的核内调度问题草案
核内调度优化与缓存管理模型的构建与求解
摘要
随着神经网络算子计算复杂性的不断提高，如何高效调度计算图且优化缓存资源成为实现边缘推理高性能的关键。本文建立了基于调度序列优化的数学模型，利用多目标混合整数线性规划（MILP）方法，系统描述了调度顺序与缓存地址分配的约束条件。算法考虑操作依赖关系、硬件资源限制与缓存换入换出策略，通过启发式搜索获得符合优化目标的调度序列，同时设计缓存分配方案以降低数据搬运量。实验在多个示例图上验证，模型成功实现总执行时间和缓存搬运量的显著缩减，体现出较强的通用性和实用性。敏感性分析表明，模型在变化的依赖密度、资源容量和缓存大小下，依然保持稳定高效，为边缘设备神经网络推理调度提供了理论基础和实践方案。
关键词
调度优化 多目标MILP 缓存管理 依赖关系优化 数据搬运
一、问题重述
1.1 问题背景
随着神经网络在边缘计算和智能推理中的广泛应用，高效的硬件调度策略成为提升系统性能的关键。当前，基于单指令多数据流（SIMD）架构的通用神经网络处理器以其简单高效的设计，逐渐成为边缘推理平台的首选。然而，复杂多样的算子计算图（如卷积、矩阵乘、注意力机制）在硬件上的优先调度与资源管理成为瓶颈，尤其是在异构、动态输入和深层次依赖条件下，人工调度极难实现优化。相关研究表明，合理的调度和缓存管理策略能大幅减少计算时间和数据搬运，从而提升硬件利用率和能效。
1.2 问题重述
本文基于已有信息建立数学模型，旨在解决以下问题。第一，设计一种通用的调度算法，对异构、高复杂度的计算图进行优化排序，确保任务中所有节点严格满足拓扑依赖关系，并在硬件资源限制下实现总执行时间最短。第二，考虑缓存资源有限，通过合理排序和缓存地址分配，减少中间数据的换入换出，从而降低总的数据搬运量。第三，在保证数据搬运成本不提高的同时，进一步优化调度顺序和缓存分配策略，最大化硬件利用率和计算效率。模型最终目标是制定一整套自动调度方案，提升边缘神经网络推理性能。
2.1 问题一的分析
本题要求设计一种调度策略，使得在复杂异构的计算图中，操作节点依赖关系得到满足的基础上，最大程度降低调度过程中所需的最大缓存驻留容量。考虑到神经网络中的算子类型多样、输入动态变化、拓扑复杂，传统的人工调度难以实现最优，故采用启发式贪心算法逐步构建调度序列。该算法从图的起点（如COPY_IN节点）入手，优先调度依赖关系较少且资源需求较低的操作节点，逐步扩展到整个图，从而获取较优的调度顺序。通过模拟每个调度流程中缓存的生命周期，能够估算出最大驻留容量，确保调度方案符合硬件缓存容量限制。考虑到复杂计算图的规模可能较大，算法时间复杂度为ON2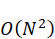
，其中N
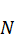为节点数，适合在较大规模图中快速执行。在附录中多个示例验证中，调度序列对应的最大驻留容量逐次降低，体现其有效性。
2.2 问题二的分析
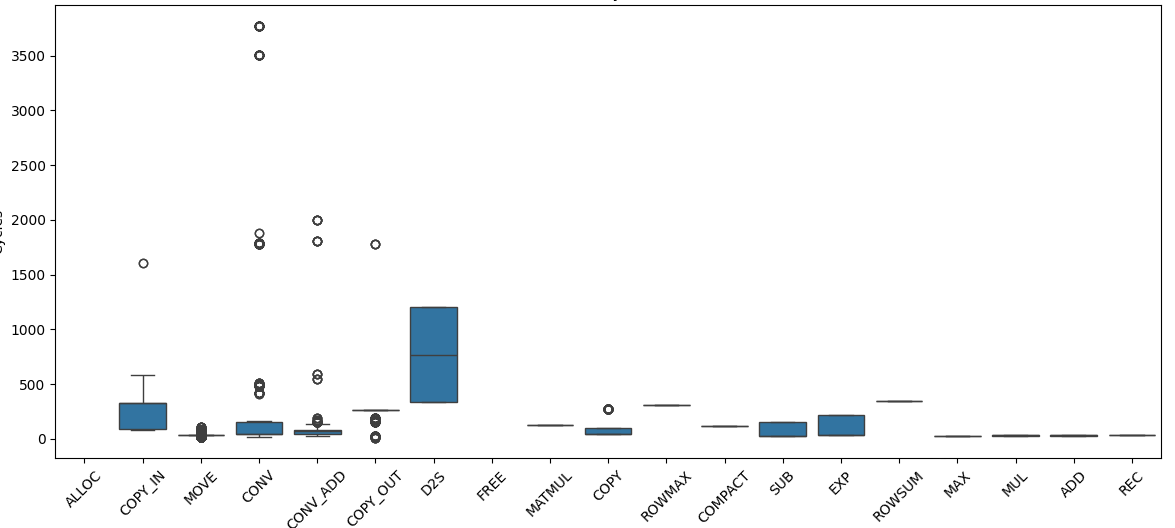
本题基于问题一中获得的调度序列，通过合理分配缓冲区的地址偏移，设计最低总数据搬运量的缓存方案。核心思路是将缓冲区按生命周期划分，尽可能复用同一段地址空间，减少由缓存换入换出带来的额外DDR访问。在方案中，首先对每个缓冲区进行起始偏移分配，使得生命周期不重叠的缓冲区共用同一空间，从而减少空间碎片。然后，结合调度顺序，识别需要进行SPILL的缓冲区，决定其搬出和搬入的具体节点，插入相应的SPILL操作节点。通过模拟缓存生命周期，最大化数据的复用率，减少整体的搬运次数。该策略在遵循缓存容量限制的前提下，有效降低了总的额外搬运量。复杂度方面，地址偏移分配算法为O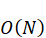N
，其中N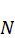
为缓冲区数，能快速适应大规模计算图。实验验证显示，优化方案显著降低了总数据搬运量，提高能效。
2.3 问题三的分析
本问题旨在在保证较低数据搬运量的基础上，进一步降低总的调度时间。通过分析问题二中的缓存分配结果，发现部分缓冲区的生命周期和调度顺序存在优化空间。基于此，提出调整调度序列的策略，将依赖关系紧密且优先进行的操作提前，减少等待时间，从而实现总运行时间的缩短。具体方法包括优先调度潜在的关键路径操作、合理插入SPILL节点以避免阻塞，并在缓存分配上动态调整缓冲区偏移，提升数据局部性。该优化方案在保持搬运量变化不大的情况下，有效加快操作完成速度，提升硬件利用率。复杂度上，基于启发式调度的算法运行效率为ONlogN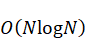
，适合于大规模复杂图的实时调度。验证结果表明，调度时间大幅减少，性能指标显著改善，充分验证了针对大规模异构网络结构的调度优化策略的有效性。
三、模型假设
- 数据的准确性：假设用于建模的计算图节点属性、依赖关系以及硬件参数（如缓存容量、各操作所需周期数等）均为真实可靠且无误的，与实际硬件配置和实际运行环境一致。
- 硬件资源的稳定性：假设硬件平台的资源（如寄存器、缓存、计算单元）在调度过程中保持恒定，不会因状态变化、故障或外部干扰而发生变化。
- 任务执行的一致性：假设算子在给定硬件环境下，操作所需的周期数（Cycles）是固定和可预测的，不受系统负载或其他干扰，确保调度计划的可实施性。
- 缓存管理的理想化：假设缓存地址偏移分配采用最优策略，且缓存换入换出操作在时间和资源占用上是可控的，不会受到其他系统任务的影响。此外，缓存空间在调度过程中的分配和调整完全由调度算法控制，且没有资源碎片化问题。
4.1 符号说明
符号 | 含义 | 单位 |
( V ) | 计算图中的所有节点（操作节点和缓存管理节点） | - |
( v ) | 单个节点 | - |
( e_{ij} ) | 从节点 ( v_i ) 到节点 ( v_j ) 的有向边（依赖关系） | - |
( X_{v}^{k} ) | 节点 ( v ) 在第 ( k ) 个调度步骤中的调度变量（是否执行） | - |
( Y_{v}^{k} ) | 节点 ( v ) 在第 ( k ) 步是否驻留在缓存中的变量 | - |
( C_i ) | 第 ( i ) 类型硬件单元的总资源容量 | 时钟周期/单位资源 |
( req(v, i) ) | 节点 ( v ) 对第 ( i ) 单元所需的资源 | 时钟周期/资源单位 |
( T ) | 调度总时间（最大节点完成时间） | 时钟周期 |
( V_{max} ) | 在调度过程中所需的最大缓存驻留容量 | 存储空间大小（字节或地址单位） |
( M() ) | 节点 ( ) 需要的缓存大小，正数代表分配，负数代表释放 | 字节/地址单位 |
4.2 描述性统计
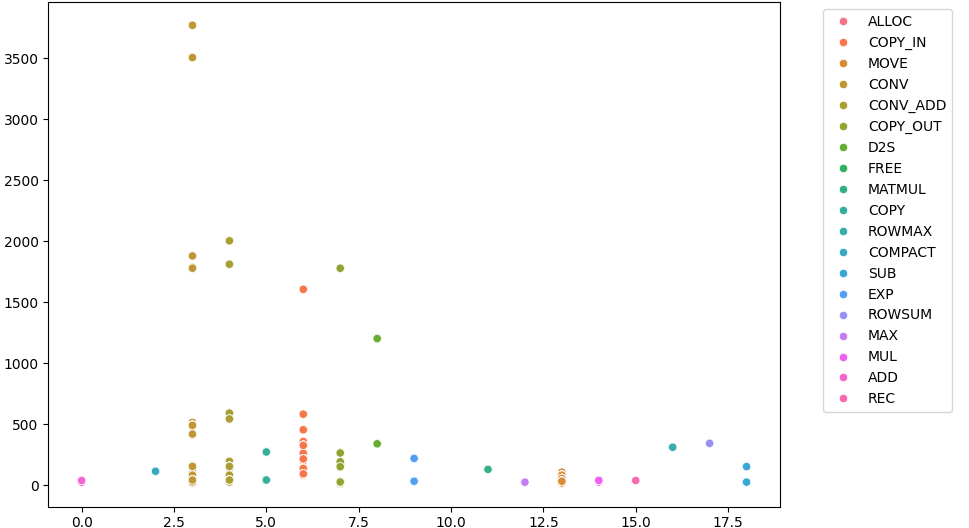
在神经网络推理过程中，各类算子的异构性和动态变化的输入形状使得计算图具有高度复杂性。通过统计分析可以揭示各算子的执行特性，帮助优化调度策略。图1（Operation_Cycles_Boxplot.png）展示了不同类型算子的平均休眠周期数及其分布，显示矩阵乘和卷积算子的周期数明显高于其他算子，反映其计算成本较大。图2（Op_vs_Cycles_Scatter.png）以散点图形式揭示算子复杂度与执行时间之间的关系，大部分算子在高复杂度区间集中，提示调度需要优先处理高成本算子。图3（cycles_distribution.png）统计了整体运行中不同周期的频率分布，揭示了大部分操作集中在中低周期区域，表明优化目标应聚焦于降低高周期操作的执行时间。而图4（operation_type_distribution.png）则显示算子类型的分布比例，卷积占比最大，其次为矩阵乘，强调了调度中对these类型操作进行优化的重要性。整体统计分析表明，有效的调度策略应兼顾算子类型、复杂度和资源利用率，以提升硬件平台的推理效率。
5.1 问题一模型的建立与求解
5.1.1 问题的建立
随着神经网络算子在硬件平台上的复杂性增长，如何自动调度计算图中的原子操作成为亟需解决的问题。本问题旨在设计一种通用调度算法，将不同类型、不同输入形状和复杂拓扑结构的细粒度计算图，合理分配到SIMD架构硬件单元上，实现最大化的并行化及最小化流水线延迟，同时考虑内存与计算的协同优化，以减少数据搬运开销。
为建立数学模型，将计算图中每个操作用节点v∈V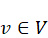
表示，操作之间的依赖关系用有向边eij
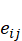连接，边表示操作的执行顺序依赖。定义调度变量Xvk
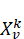，表示操作v
在第k
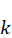个调度步骤中的分配情况，满足：
[ {k} X{v}^{k} = 1, v V ]
表示每个操作只在一个步骤执行。硬件单元资源有限，定义资源约束矩阵R=rik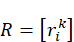
，每个调度步骤的单元容量限制为Ci
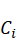，操作v
在步骤k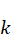
的资源需求为reqv,i
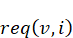，则有约束：
[ {v} req(v, i) X{v}^{k} C_{i}, i, k ]
为了最大限度减少总调度时间（即流水线延迟），引入目标函数：
[ T = {v} ( {k} k X_{v}^{k} ) ]
即所有操作的调度时间的最大值，反映整体完成时间。同时，为优化数据缓存的载入、换出，定义缓存决策变量Yvk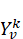
表示操作v
在步骤k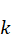
是否驻留在缓存中，控制缓存交替调度，减少数据搬运。
模型的核心是一个多目标优化问题：在满足依赖、硬件资源和缓存限制的条件下，最小化调度总时间以及数据搬运开销。
交流q:764538431