磁共振成像原理(理论)8:射频回波 (RF Echoes)-三脉冲回波(1)
α1−τ1−α2−τ2−α3\alpha_{1}-\tau_{1}-\alpha_{2}-\tau_{2}-\alpha_{3}α1−τ1−α2−τ2−α3 三脉冲回波 ( Three-Pulse Echoes)
下面定义了通用的三脉冲序列,α1,α2,α3\alpha_1, \alpha_2, \alpha_3α1,α2,α3: 三个任意角度的射频脉冲,τ1,τ2\tau_1, \tau_2τ1,τ2: 两个时间间隔
α1−τ1−α2−τ2−α3(4.36) \alpha_{1}-\tau_{1}-\alpha_{2}-\tau_{2}-\alpha_{3} \tag {4.36} α1−τ1−α2−τ2−α3(4.36)
该序列最多可产生五个回波:三个常规自旋回波 (SE)、一个次级自旋回波 (SSE)和一个受激回波(STE),如下图所示:
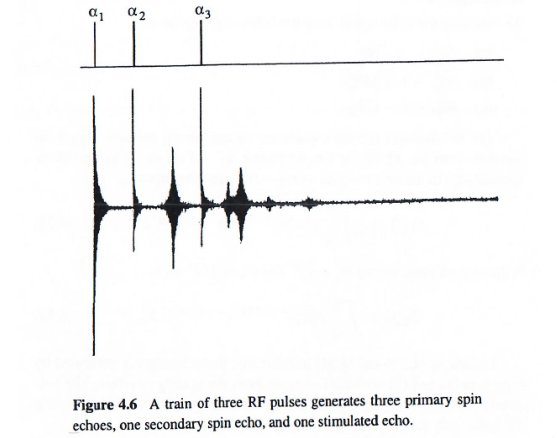
忽略脉冲大小和回波的大小,我们得到如下脉冲和回波的时序图
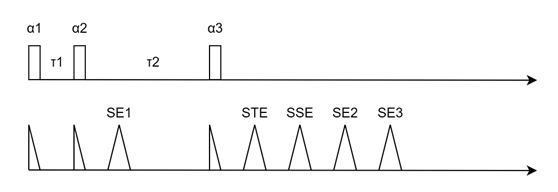
其中:
-
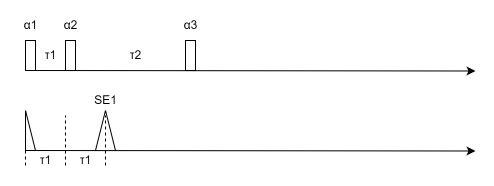
SE1 (第一自旋回波): 由脉冲 α1\alpha_1α1 和 α2\alpha_2α2 产生,位于 t=2τ1t = 2\tau_1t=2τ1,如下图所示, α1\alpha_1α1脉冲的FID信号由 α2\alpha_2α2 镜像到SE1。该回波正是式子(4.29)中的第一项。
-
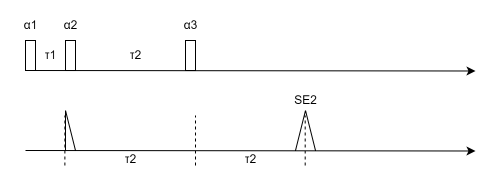
SE2 (第二自旋回波): 由脉冲 α2\alpha_2α2 和 α3\alpha_3α3 产生,位于 t=τ1+2τ2t = \tau_1 + 2\tau_2t=τ1+2τ2,如下图所示, α2\alpha_2α2 脉冲的FID信号由 α3\alpha_3α3 镜像到SE2。该回波正是式子(4.29)中的第三项,它被第三个脉冲翻转后又重新聚相了。
-
SE3 (第三自旋回波): 由脉冲 α1\alpha_1α1 和 α3\alpha_3α3 产生,位于 t=2(τ1+τ2)t = 2(\tau_1 + \tau_2)t=2(τ1+τ2),如下图所示, α1\alpha_1α1 脉冲的FID信号由 α3\alpha_3α3 镜像到SE3。该回波正是式子(4.29)中的第二项,它被第三个脉冲翻转后又重新聚相了。
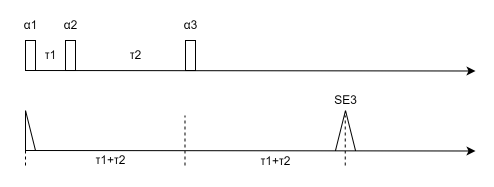
-
次级回波 (Secondary Echo): 当 τ2>2τ1\tau_2 > 2\tau_1τ2>2τ1 时,第一个回波 (SE1) 发生在第二和第三脉冲之间。第三个脉冲 (α3\alpha_3α3) 会“镜像”这个已存在的 SE1 信号,从而在 t=2τ2t = 2\tau_2t=2τ2 时刻(即第三脉冲后 τ2−τ1\tau_2 - \tau_1τ2−τ1 时刻)产生一个次级回波,如下图所示。该回波正是式子(4.29)中的第一项(SE1),它被第三个脉冲翻转后又重新聚相了。
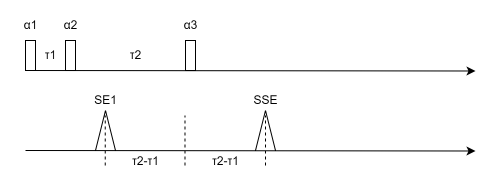
-
受激回波 (Stimulated Echo, STE): 由所有三个脉冲 (α1,α2,α3\alpha_1, \alpha_2, \alpha_3α1,α2,α3) 共同作用产生。其独特之处在于,第二部分磁化在 τ2\tau_2τ2 期间是以纵向磁化的形式存在的,因此其信号幅度的衰减主要受较慢的 T1T_1T1 弛豫影响,而非较快的 T2T_2T2 弛豫,如下图所示:
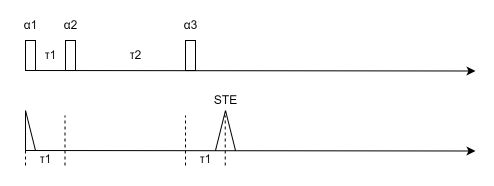
三个SE和1个SSE都比较容易理解,他们都是基于受激后的FID信号被后续的脉冲信号的镜像产生的回波。但是受激回波STE的产生机理比较特殊,为清晰理解受激回波的发生过程,我们暂设 α1=α2=α3=90∘\alpha_{1}=\alpha_{2}=\alpha_{3}=90^{\circ}α1=α2=α3=90∘。第一个脉冲后,平衡磁化矢量 Mz0M_{z}^{0}Mz0 被完全翻转至横向平面。如果 τ1\tau_{1}τ1 在 T2T_{2}T2 量级或更短,则在 τ1\tau_{1}τ1 时刻我们仍会有可观的横向磁化矢量。因此,第二个 90∘90^{\circ}90∘ 脉冲,除了会诱发第一个自旋回波(SE)外,还会产生一个纵向磁化矢量。在第二个脉冲之后的 τ2\tau_{2}τ2 期间,这部分磁化矢量被“存储”在 z′z^{\prime}z′ 轴上,同时经历纵向弛豫过程。在 τ2\tau_{2}τ2 间隔结束时施加的第三个 90∘90^{\circ}90∘ 脉冲,又将这部分存储的纵向磁化矢量重新旋转回横向平面。由于等色团的固有属性并未被这些磁化矢量的复杂变换所改变,它们在第三个脉冲后将以与第二个脉冲前相同的速率和方向进动。此外,这部分磁化矢量仅在 τ1\tau_{1}τ1 期间受到磁场不均匀性的影响。因此,这些等色团矢量间的相长干涉将在第三个脉冲后的 t=τ1t=\tau_{1}t=τ1 时刻达到最大值,受激回波由此形成。
下面来完整的推导一遍,先来推导第二个脉冲后的横向和纵向的磁化分量演变:
t>τ1+t > \tau_{1+}t>τ1+:磁化分量
**t>τ1+t > \tau_{1+}t>τ1+:横向磁化分量
公式(4.29)描述了在双脉冲序列(α1−τ1−α2\alpha_1 - \tau_1 - \alpha_2α1−τ1−α2)中,第二个脉冲α2\alpha_2α2施加后 (t>τ1+t > \tau_{1+}t>τ1+) 横向磁化分量,将其重写如下(将之前双脉冲的时间间隔τ→τ1\tau \rightarrow \tau_1τ→τ1):
Mx′y′(ω,t)=Mz0(ω)sinα1sin2α22e−t/T2e−iω(t−2τ1)−Mz0(ω)sinα1cos2α22e−t/T2e−iωt−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(t−τ1)/T2e−iω(t−τ1)(4.37a)
\begin{aligned}
M_{x^{\prime}y^{\prime}}(\omega,t) = & M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} e^{-t/T_{2}} e^{-i\omega(t-2\tau_{1})} \\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} e^{-t/T_{2}} e^{-i\omega t} \\
& -M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_{1}/T_{1}}\right] \sin\alpha_{2} e^{-(t-\tau_{1})/T_{2}} e^{-i\omega(t-\tau_{1})}
\end{aligned}
\tag{4.37a}
Mx′y′(ω,t)=Mz0(ω)sinα1sin22α2e−t/T2e−iω(t−2τ1)−Mz0(ω)sinα1cos22α2e−t/T2e−iωt−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(t−τ1)/T2e−iω(t−τ1)(4.37a)
**t>τ1+t > \tau_{1+}t>τ1+:纵向磁化分量
公式 (4.25b) 描述了在双脉冲序列 (α1−τ1−α2\alpha_1 - \tau_1 - \alpha_2α1−τ1−α2) 中,第二个脉冲 (α2\alpha_2α2) 施加后瞬间 (t=τ1+t = \tau_{1+}t=τ1+) 的纵向磁化分量,,将其重写如下(将之前双脉冲的时间间隔τ→τ1\tau \rightarrow \tau_1τ→τ1):
Mz′(ω,τ1+)=Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2
\begin{aligned}
M_{z^{\prime}}\left(\omega,\tau_{1+}\right)= & M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_1 /T_{1}}\right]\cos\alpha_{2} \\
& - M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_1 e^{-\tau_1 /T_{2}}
\end{aligned}
Mz′(ω,τ1+)=Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2
为简化后续推导,我们将其写为两项之和:
Mz′(ω,τ1+)=A−B
M_{z^{\prime}}(\omega, \tau_{1+}) = A - B
Mz′(ω,τ1+)=A−B
其中:
- A=Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2A = M_{z}^{0}(\omega)\left[1 - (1 - \cos\alpha_{1}) e^{-\tau_1 /T_{1}}\right]\cos\alpha_{2}A=Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2
- B=Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2B = M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_1 e^{-\tau_1 /T_{2}}B=Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2
公式 (4.23) 描述了在自由进动(无射频脉冲)期间,磁化矢量随时间的演化重写如下:
[Mx′(0)My′(0)Mz′(0)]⟶τ[Mx′(τ)My′(τ)Mz′(τ)]=[(Mx′(0)cosωτ+My′(0)sinωτ)e−τ/T2(−Mx′(0)sinωτ+My′(0)cosωτ)e−τ/T2Mz0(1−e−τ/T1)+Mz′(0)e−τ/T1]
\begin{bmatrix}
M_{x^{\prime}}(0) \\
M_{y^{\prime}}(0) \\
M_{z^{\prime}}(0)
\end{bmatrix}
\stackrel{{\tau}}{\longrightarrow}
\begin{bmatrix}
M_{x^{\prime}}(\tau) \\
M_{y^{\prime}}(\tau) \\
M_{z^{\prime}}(\tau)
\end{bmatrix} =
\begin{bmatrix}
(M_{x^{\prime}}(0)\cos\omega\tau + M_{y^{\prime}}(0)\sin\omega\tau)e^{-\tau/T_{2}} \\
(-M_{x^{\prime}}(0)\sin\omega\tau + M_{y^{\prime}}(0)\cos\omega\tau)e^{-\tau/T_{2}} \\
M_{z}^{0}(1 - e^{-\tau/T_{1}}) + M_{z^{\prime}}(0)e^{-\tau/T_{1}} \end{bmatrix} Mx′(0)My′(0)Mz′(0)⟶τMx′(τ)My′(τ)Mz′(τ)=(Mx′(0)cosωτ+My′(0)sinωτ)e−τ/T2(−Mx′(0)sinωτ+My′(0)cosωτ)e−τ/T2Mz0(1−e−τ/T1)+Mz′(0)e−τ/T1
其纵向分量 (Mz′M_{z'}Mz′) 的演化规则为:
Mz′→ΔtMz0(1−e−Δt/T1)+Mz′e−Δt/T1
M_{z^{\prime}} \xrightarrow{\Delta t} M_{z}^{0}\left(1 - e^{-\Delta t /T_{1}}\right) + M_{z^{\prime}} e^{-\Delta t /T_{1}}
Mz′ΔtMz0(1−e−Δt/T1)+Mz′e−Δt/T1
在我们的问题中,演化时间 Δt=t−τ1\Delta t = t - \tau_1Δt=t−τ1(从第二个脉冲结束开始计时)。
我们将初始条件 Mz′(ω,τ1+)M_{z^{\prime}}(\omega, \tau_{1+})Mz′(ω,τ1+) 作为起点,应用上述演化规则,计算其演化到任意时刻 t>τ1t > \tau_1t>τ1 的结果:
Mz′(ω,t)=Mz0(ω)(1−e−(t−τ1)/T1)+Mz′(ω,τ1+)e−(t−τ1)/T1=Mz0(ω)(1−e−(t−τ1)/T1)+(A−B)e−(t−τ1)/T1=Mz0(ω)(1−e−(t−τ1)/T1)+A⋅e−(t−τ1)/T1−B⋅e−(t−τ1)/T1
\begin{aligned}
M_{z^{\prime}}(\omega, t) &= M_{z}^{0}(\omega)\left(1 - e^{-(t - \tau_1) /T_{1}}\right) + M_{z^{\prime}}(\omega, \tau_{1+}) e^{-(t - \tau_1) /T_{1}} \\
&= M_{z}^{0}(\omega)\left(1 - e^{-(t - \tau_1) /T_{1}}\right) + (A - B) e^{-(t - \tau_1) /T_{1}} \\
&= M_{z}^{0}(\omega)\left(1 - e^{-(t - \tau_1) /T_{1}}\right) + \textcolor{red}{A} \cdot e^{-(t - \tau_1) /T_{1}} - \textcolor{blue}{B} \cdot e^{-(t - \tau_1) /T_{1}}
\end{aligned}
Mz′(ω,t)=Mz0(ω)(1−e−(t−τ1)/T1)+Mz′(ω,τ1+)e−(t−τ1)/T1=Mz0(ω)(1−e−(t−τ1)/T1)+(A−B)e−(t−τ1)/T1=Mz0(ω)(1−e−(t−τ1)/T1)+A⋅e−(t−τ1)/T1−B⋅e−(t−τ1)/T1
将 AAA 和 BBB 的具体表达式代入:
Mz′(ω,t)=Mz0(ω)(1−e−(t−τ1)/T1)+{Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2}e−(t−τ1)/T1−{Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2}e−(t−τ1)/T1
\begin{aligned}
M_{z^{\prime}}(\omega, t) = & M_{z}^{0}(\omega)\left(1 - e^{-(t - \tau_1) /T_{1}}\right) \\
& + \textcolor{red}{\left\{ M_{z}^{0}(\omega)\left[1 - (1 - \cos\alpha_{1}) e^{-\tau_1 /T_{1}}\right]\cos\alpha_{2} \right\} }e^{-(t - \tau_1) /T_{1}} \\
& - \textcolor{blue}{\left\{ M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_1 e^{-\tau_1 /T_{2}} \right\}} e^{-(t - \tau_1) /T_{1}}
\end{aligned}
Mz′(ω,t)=Mz0(ω)(1−e−(t−τ1)/T1)+{Mz0(ω)[1−(1−cosα1)e−τ1/T1]cosα2}e−(t−τ1)/T1−{Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2}e−(t−τ1)/T1
展开括号并合并同类项:
Mz′(ω,t)=Mz0(ω)−Mz0(ω)e−(t−τ1)/T1+Mz0(ω)cosα2e−(t−τ1)/T1−Mz0(ω)cosα2(1−cosα1)e−τ1/T1e−(t−τ1)/T1−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1
\begin{aligned}
M_{z^{\prime}}(\omega, t) = & M_{z}^{0}(\omega) \\
& - M_{z}^{0}(\omega)e^{-(t - \tau_1) /T_{1}} \\
& + M_{z}^{0}(\omega)\cos\alpha_{2} e^{-(t - \tau_1) /T_{1}} \\
& - M_{z}^{0}(\omega)\cos\alpha_{2}(1 - \cos\alpha_{1}) e^{-\tau_1 /T_{1}} e^{-(t - \tau_1) /T_{1}} \\
& - M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_1 e^{-\tau_1 /T_{2}} e^{-(t - \tau_1) /T_{1}}
\end{aligned}
Mz′(ω,t)=Mz0(ω)−Mz0(ω)e−(t−τ1)/T1+Mz0(ω)cosα2e−(t−τ1)/T1−Mz0(ω)cosα2(1−cosα1)e−τ1/T1e−(t−τ1)/T1−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1
进行合并,并重新排列各项的顺序:
Mz′(ω,t)=Mz0(ω)−Mz0(ω)(1−cosα2)e−(t−τ1)/T1−Mz0(ω)(1−cosα1)cosα2e−t/T1−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1
\begin{aligned}
M_{z^{\prime}}(\omega, t) = & M_{z}^{0}(\omega) \\
& - M_{z}^{0}(\omega)(1 - \cos\alpha_{2}) e^{-(t - \tau_1) /T_{1}} \\
& - M_{z}^{0}(\omega)(1 - \cos\alpha_{1})\cos\alpha_{2} e^{-t /T_{1}} \\
& - M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_1 e^{-\tau_1 /T_{2}} e^{-(t - \tau_1) /T_{1}}
\end{aligned}
Mz′(ω,t)=Mz0(ω)−Mz0(ω)(1−cosα2)e−(t−τ1)/T1−Mz0(ω)(1−cosα1)cosα2e−t/T1−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1
最后,将前三项合并到一个括号内,即可得到最终的公式 (4.37b),即第二个脉冲α2\alpha_2α2施加后 (t>τ1+t > \tau_{1+}t>τ1+) 纵向磁化分量:
Mz′(ω,t)=Mz0(ω)[1−(1−cosα2)e−(t−τ1)/T1−(1−cosα1)cosα2e−t/T1]−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1(4.37b)
\begin{aligned}
M_{z^{\prime}}(\omega,t) = & M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{2}\right) e^{-(t-\tau_{1})/T_{1}} - \left(1-\cos\alpha_{1}\right)\cos\alpha_{2} e^{-t/T_{1}}\right] \\
& \textcolor{red}{-M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_{1} e^{-\tau_{1}/T_{2}} e^{-(t-\tau_{1})/T_{1}}}
\end{aligned}
\tag{4.37b}
Mz′(ω,t)=Mz0(ω)[1−(1−cosα2)e−(t−τ1)/T1−(1−cosα1)cosα2e−t/T1]−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1(4.37b)
其中−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1\textcolor{red}{-M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_{1} e^{-\tau_{1}/T_{2}} e^{-(t-\tau_{1})/T_{1}}}−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−(t−τ1)/T1:包含了相位项,此项是形成受激回波的关键,因为它编码了频率信息 (cosωτ1\cos\omega\tau_1cosωτ1) 并以纵向磁化的形式“存储”起来,其衰减受 T1T_1T1 主导。这使得这部分的分量被很大程度的保留下来,因为T2<<T1T_2<<T_1T2<<T1。
t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2:磁化分量
下面用个办法推导在t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2时刻的x′,y′x',y'x′,y′方向磁化分量:
**t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2:x′,y′x',y'x′,y′方向磁化分量方法一
从(4.37a)反向推导,这也是教材中采用的办法,只是这样推导出来和教材中的有个符号的差别。首先是将**t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2代入(4.37a)可得:
Mx′y′(ω,τ1+τ2)=Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2e−iω((τ1+τ2)−2τ1)−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2e−iω(τ1+τ2))−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(τ1+τ2)−τ1)/T2e−iω((τ1+τ2)−τ1)=Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2e−iω(τ2−τ1)−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2e−iω(τ1+τ2))−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.37a)
\begin{aligned}
M_{x^{\prime}y^{\prime}}(\omega,\tau_{1}+\tau_{2}) = & M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} e^{-i\omega((\tau_{1}+\tau_{2})-2\tau_{1})} \\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} e^{-i\omega (\tau_{1}+\tau_{2}))} \\
& -M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_{1}/T_{1}}\right] \sin\alpha_{2} e^{-(\tau_{1}+\tau_{2})-\tau_{1})/T_{2}} e^{-i\omega((\tau_{1}+\tau_{2})-\tau_{1})}\\
\\
= & M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{red}{e^{-i\omega(\tau_{2}-\tau_{1})}} \\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{blue}{e^{-i\omega (\tau_{1}+\tau_{2}))} }\\
& -M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_{1}/T_{1}}\right] \sin\alpha_{2} e^{-(2\tau_{1}+\tau_{2}))/T_{2}} \textcolor{purple}{e^{-i\omega(\tau_{2})}}
\end{aligned}
\tag{4.37a}
Mx′y′(ω,τ1+τ2)==Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2e−iω((τ1+τ2)−2τ1)−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2e−iω(τ1+τ2))−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(τ1+τ2)−τ1)/T2e−iω((τ1+τ2)−τ1)Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2e−iω(τ2−τ1)−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2e−iω(τ1+τ2))−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.37a)
利用欧拉公式
e−iωτ=cosωτ−isinωτeiωτ=cosωτ+isinωτ
\begin{align*}
e^{-i\omega\tau}&=\cos\omega\tau-i\sin\omega\tau \\
e^{i\omega\tau}&=\cos\omega\tau+i\sin\omega\tau
\end{align*} e−iωτeiωτ=cosωτ−isinωτ=cosωτ+isinωτ
将Mx′y′(ω,τ1+τ2)M_{x^{\prime}y^{\prime}}(\omega,\tau_{1}+\tau_{2})Mx′y′(ω,τ1+τ2)展开为复数形式
Mx′y′(ω,τ1+τ2)=Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2[cosω(τ2−τ1)−isinω(τ2−τ1)]−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2[cosω(τ2+τ1)−isinω(τ2+τ1)]−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.37a)
\begin{aligned}
M_{x^{\prime}y^{\prime}}(\omega,\tau_{1}+\tau_{2})&=\\
& M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{red}{[\cos\omega(\tau_{2}-\tau_{1})-i\sin\omega(\tau_{2}-\tau_{1})]} \\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{blue}{[\cos\omega(\tau_{2}+\tau_{1})-i\sin\omega(\tau_{2}+\tau_{1})]}\\
& -M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_{1}/T_{1}}\right] \sin\alpha_{2} e^{-(2\tau_{1}+\tau_{2}))/T_{2}} \textcolor{purple}{e^{-i\omega(\tau_{2})}}\\
\end{aligned}
\tag{4.37a}
Mx′y′(ω,τ1+τ2)=Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2[cosω(τ2−τ1)−isinω(τ2−τ1)]−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2[cosω(τ2+τ1)−isinω(τ2+τ1)]−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.37a)
其中实数部分为x′x'x′方向磁化分量:
Mx′(ω,τ1+τ2)=Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2cosω(τ2−τ1)−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2cosω(τ2+τ1)−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.38)
\begin{aligned}
M_{x^{\prime}}(\omega, \tau_{1}+\tau_{2}) =& M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{red}{\cos\omega(\tau_{2}-\tau_{1})} \\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} e^{-(\tau_{1}+\tau_{2})/T_{2}} \textcolor{blue}{\cos\omega(\tau_{2}+\tau_{1})}\\
& -M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{1}\right) e^{-\tau_{1}/T_{1}}\right] \sin\alpha_{2} e^{-(2\tau_{1}+\tau_{2}))/T_{2}} \textcolor{purple}{e^{-i\omega(\tau_{2})}}\\
\end{aligned}
\tag{4.38}
Mx′(ω,τ1+τ2)=Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2cosω(τ2−τ1)−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2cosω(τ2+τ1)−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2e−(2τ1+τ2))/T2e−iω(τ2)(4.38)
其中虚数部分为y′y'y′方向磁化分量:
My′(ω,τ1+τ2)=Mz0(ω)sinα1cos2α22sinω(τ1+τ2)e−(τ1+τ2)/T2−Mz0(ω)sinα1sin2α22sinω(τ2−τ1)e−(τ1+τ2)/T2+Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2(4.39)
\begin{aligned}
M_{y^{\prime}}(\omega, \tau_{1}+\tau_{2}) = & M_{z}^{0}(\omega) \sin \alpha_{1} \cos ^{2} \frac{\alpha_{2}}{2} \textcolor{blue}{\sin \omega\left(\tau_{1}+\tau_{2}\right)} e^{-\left(\tau_{1}+\tau_{2}\right) / T_{2}} \\
& -M_{z}^{0}(\omega) \sin \alpha_{1} \sin ^{2} \frac{\alpha_{2}}{2} \textcolor{red}{\sin \omega\left(\tau_{2}-\tau_{1}\right)} e^{-\left(\tau_{1}+\tau_{2}\right) / T_{2}} \\
& +M_{z}^{0}(\omega)\left[1-\left(1-\cos \alpha_{1}\right) e^{-\tau_{1} / T_{1}}\right] \sin \alpha_{2} \sin \omega \tau_{2} e^{-\tau_{2} / T_{2}}
\end{aligned}
\tag{4.39}
My′(ω,τ1+τ2)=Mz0(ω)sinα1cos22α2sinω(τ1+τ2)e−(τ1+τ2)/T2−Mz0(ω)sinα1sin22α2sinω(τ2−τ1)e−(τ1+τ2)/T2+Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2(4.39)
**t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2:x′,y′x',y'x′,y′方向磁化分量方法二
从式(4.26)和式(4.27)正向推导。
公式 (4.26) 描述了在双脉冲序列 (α1−τ1−α2\alpha_1 - \tau_1 - \alpha_2α1−τ1−α2) 中,第二个脉冲 (α2\alpha_2α2) 施加后瞬间 (t=τ1+t = \tau_{1+}t=τ1+) 的x′x'x′方向磁化分量,,将其重写如下(将之前双脉冲的时间间隔τ→τ1\tau \rightarrow \tau_1τ→τ1):
Mx′(ω,τ1+)=−Mz0(ω)sinα1cos2α22cosωτ1e−τ1/T2+Mz0(ω)sinα1sin2α22cosωτ1e−τ1/T2−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2 \begin{align*}
M_{x^{\prime}}(\omega, \tau_{1+}) &= -M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}} \\
&\quad + M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}} \\
&\quad - M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}
\end{align*} Mx′(ω,τ1+)=−Mz0(ω)sinα1cos22α2cosωτ1e−τ1/T2+Mz0(ω)sinα1sin22α2cosωτ1e−τ1/T2−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2
公式 (4.27) 描述了在双脉冲序列 (α1−τ1−α2\alpha_1 - \tau_1 - \alpha_2α1−τ1−α2) 中,第二个脉冲 (α2\alpha_2α2) 施加后瞬间 (t=τ1+t = \tau_{1+}t=τ1+) 的y′y'y′方向磁化分量,将其重写如下(将之前双脉冲的时间间隔τ→τ1\tau \rightarrow \tau_1τ→τ1):
My′(ω,τ1+)=Mz0(ω)sinα1cos2α22sinωτ1e−τ1/T2+Mz0(ω)sinα1sin2α22sinωτ1e−τ1/T2 \begin{align*}
M_{y^{\prime}}(\omega,\tau_{1+})&=M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}\\
&\quad+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}
\end{align*}My′(ω,τ1+)=Mz0(ω)sinα1cos22α2sinωτ1e−τ1/T2+Mz0(ω)sinα1sin22α2sinωτ1e−τ1/T2
经过 τ2\tau_2τ2 延迟后(应用4.23),x′x'x′磁化分量演化为:
Mx′(ω,τ1+τ2)=[Mx′(ω,τ1+)cosωτ2+My′(ω,τ1+)sinωτ2]e−τ2/T2={−Mz0(ω)sinα1cos2α22cosωτ1e−τ1/T2+Mz0(ω)sinα1sin2α22cosωτ1e−τ1/T2−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2}⋅cosωτ2⋅e−τ2/T2+{Mz0(ω)sinα1cos2α22sinωτ1e−τ1/T2+Mz0(ω)sinα1sin2α22sinωτ1e−τ1/T2}⋅sinωτ2e−τ2/T2=−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2[cosωτ1cosωτ2−sinωτ1sinωτ2]+Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2[cosωτ1cosωτ2+sinωτ1sinωτ2]−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2cosωτ2e−τ2/T2=−Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2cosω(τ1+τ2)+Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2cosω(τ1−τ2)−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2cosωτ2e−τ2/T2 \begin{align*}
M_{x^{\prime}}(\omega, \tau_1 + \tau_2)
&=[\textcolor{red}{M_{x^{\prime}}(\omega,\tau_{1+})}\cos\omega\tau_{2} + \textcolor{blue}{M_{y^{\prime}}(\omega,\tau_{1+})}\sin\omega\tau_{2}]e^{-\tau_{2}/T_{2}}\\
&=\{\textcolor{red}{-M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}}} \\
&\quad \textcolor{red}{+ M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}}} \\
&\quad \textcolor{red}{- M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}}\} \cdot \cos\omega\tau_{2} \cdot e^{-\tau_{2}/T_{2}} \\
&\quad+\{\textcolor{blue}{M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}}\\
&\quad\textcolor{blue}{+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}}\} \cdot \sin\omega\tau_{2}e^{-\tau_{2}/T_{2}}\\
\\
&=-M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}[\cos\omega\tau_{1}\cos\omega\tau_{2}-\sin\omega\tau_{1}\sin\omega\tau_{2}]\\
&\quad+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}[\cos\omega\tau_{1}\cos\omega\tau_{2}+\sin\omega\tau_{1}\sin\omega\tau_{2}]\\
&\quad {- M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}} \cos\omega\tau_{2}e^{-\tau_{2}/T_{2}} \\
\\
&=-M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}\cos\omega(\tau_{1}+\tau_{2})\\
&\quad+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}\cos\omega(\tau_{1}-\tau_{2})\\
&\quad {- M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}} \cos\omega\tau_{2}e^{-\tau_{2}/T_{2}} \\
\end{align*} Mx′(ω,τ1+τ2)=[Mx′(ω,τ1+)cosωτ2+My′(ω,τ1+)sinωτ2]e−τ2/T2={−Mz0(ω)sinα1cos22α2cosωτ1e−τ1/T2+Mz0(ω)sinα1sin22α2cosωτ1e−τ1/T2−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2}⋅cosωτ2⋅e−τ2/T2+{Mz0(ω)sinα1cos22α2sinωτ1e−τ1/T2+Mz0(ω)sinα1sin22α2sinωτ1e−τ1/T2}⋅sinωτ2e−τ2/T2=−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2[cosωτ1cosωτ2−sinωτ1sinωτ2]+Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2[cosωτ1cosωτ2+sinωτ1sinωτ2]−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2cosωτ2e−τ2/T2=−Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2cosω(τ1+τ2)+Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2cosω(τ1−τ2)−Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2cosωτ2e−τ2/T2
此式和(4.38)一样,证明推导过程是正确的。
经过 τ2\tau_2τ2 延迟后(应用4.23),y′y'y′磁化分量演化为:
My′(ω,τ1+τ2)=[−Mx′(ω,τ1+)sinωτ2+My′(ω,τ1+)cosωτ2]e−τ2/T2={Mz0(ω)sinα1cos2α22cosωτ1e−τ1/T2−Mz0(ω)sinα1sin2α22cosωτ1e−τ1/T2+Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2}⋅sinωτ2⋅e−τ2/T2+{Mz0(ω)sinα1cos2α22sinωτ1e−τ1/T2+Mz0(ω)sinα1sin2α22sinωτ1e−τ1/T2}⋅cosωτ2e−τ2/T2=Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2[cosωτ1sinωτ2+sinωτ1cosωτ2]−Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2[cosωτ1sinωτ2−sinωτ1cosωτ2]Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2=Mz0(ω)sinα1cos2α22e−(τ1+τ2)/T2sinω(τ1+τ2)−Mz0(ω)sinα1sin2α22e−(τ1+τ2)/T2sinω(τ1−τ2)Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2 \begin{align*}
M_{y^{\prime}}(\omega, \tau_1 + \tau_2)
&=[\textcolor{red}{-M_{x^{\prime}}(\omega,\tau_{1+})}\sin\omega\tau_{2} + \textcolor{blue}{M_{y^{\prime}}(\omega,\tau_{1+})}\cos\omega\tau_{2}]e^{-\tau_{2}/T_{2}}\\
&=\{\textcolor{red}{M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}}} \\
&\quad \textcolor{red}{- M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2} \cos\omega\tau_{1} e^{-\tau_{1}/T_{2}}} \\
&\quad \textcolor{red}{+ M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}}\} \cdot \sin\omega\tau_{2} \cdot e^{-\tau_{2}/T_{2}} \\
&\quad+\{\textcolor{blue}{M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}}\\
&\quad\textcolor{blue}{+M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}\sin\omega\tau_{1} e^{-\tau_{1}/T_{2}}}\} \cdot \cos\omega\tau_{2}e^{-\tau_{2}/T_{2}}\\
\\
&=M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}[\cos\omega\tau_{1}\sin\omega\tau_{2}+\sin\omega\tau_{1}\cos\omega\tau_{2}]\\
&\quad-M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}[\cos\omega\tau_{1}\sin\omega\tau_{2}-\sin\omega\tau_{1}\cos\omega\tau_{2}]\\
&\quad {M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}} \sin\omega\tau_{2}e^{-\tau_{2}/T_{2}} \\
\\
&=M_{z}^{0}(\omega)\sin\alpha_{1}\cos^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}\sin\omega(\tau_{1}+\tau_{2})\\
&\quad-M_{z}^{0}(\omega)\sin\alpha_{1}\sin^{2}\frac{\alpha_{2}}{2}e^{-(\tau_{1}+\tau_{2})/T_{2}}\sin\omega(\tau_{1}-\tau_{2})\\
&\quad {M_{z}^{0}(\omega)[1 - (1 - \cos\alpha_{1})e^{-\tau_{1}/T_{1}}] \sin\alpha_{2}} \sin\omega\tau_{2}e^{-\tau_{2}/T_{2}} \\
\end{align*} My′(ω,τ1+τ2)=[−Mx′(ω,τ1+)sinωτ2+My′(ω,τ1+)cosωτ2]e−τ2/T2={Mz0(ω)sinα1cos22α2cosωτ1e−τ1/T2−Mz0(ω)sinα1sin22α2cosωτ1e−τ1/T2+Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2}⋅sinωτ2⋅e−τ2/T2+{Mz0(ω)sinα1cos22α2sinωτ1e−τ1/T2+Mz0(ω)sinα1sin22α2sinωτ1e−τ1/T2}⋅cosωτ2e−τ2/T2=Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2[cosωτ1sinωτ2+sinωτ1cosωτ2]−Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2[cosωτ1sinωτ2−sinωτ1cosωτ2]Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2=Mz0(ω)sinα1cos22α2e−(τ1+τ2)/T2sinω(τ1+τ2)−Mz0(ω)sinα1sin22α2e−(τ1+τ2)/T2sinω(τ1−τ2)Mz0(ω)[1−(1−cosα1)e−τ1/T1]sinα2sinωτ2e−τ2/T2
此式和(4.39)一样,证明推导过程是正确的。
总结:我们用两种方式分别验证了t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2:x′,y′x',y'x′,y′方向磁化分量
**t=τ1+τ2t = \tau_1 + \tau_2t=τ1+τ2:z′z'z′方向磁化分量
z′z'z′方向磁化分量:
Mz′(ω,τ1+τ2)=Mz0(ω)[1−(1−cosα2)e−τ2/T1−(1−cosα1)cosα2e−(τ1+τ2)/T1]−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−τ2/T1(4.40) \begin{aligned}
M_{z^{\prime}}(\omega, &\tau_{1}+\tau_{2})\\
= &M_{z}^{0}(\omega)\left[1-\left(1-\cos\alpha_{2}\right) e^{-\tau_{2} /T_{1}}-\left(1-\cos\alpha_{1}\right)\cos\alpha_{2} e^{-\left(\tau_{1}+\tau_{2}\right) /T_{1}}\right]\\
& -M_{z}^{0}(\omega)\sin\alpha_{1}\sin\alpha_{2}\cos\omega\tau_{1} e^{-\tau_{1} /T_{2}}e^{-\tau_{2} /T_{1}}
\end{aligned}
\tag{4.40}
Mz′(ω,=τ1+τ2)Mz0(ω)[1−(1−cosα2)e−τ2/T1−(1−cosα1)cosα2e−(τ1+τ2)/T1]−Mz0(ω)sinα1sinα2cosωτ1e−τ1/T2e−τ2/T1(4.40)
写不下了,分成两篇
