高频面试题——深入掌握栈和队列的数据结构技巧
栈和队列这俩货,存的都是 “一对一” 逻辑关系的数据,说白了,它们本质上都属于线性存储结构。只不过脾气不一样:栈讲究 “先进后出”,就像叠盘子,先放进去的在底下,最后才能拿出来;队列则是 “先进先出”,好比排队打饭,先来的先打,打完就走。
要说这俩货的存储方式,可都是"线性表界的特种兵",只不过一个玩顺序存储(顺序栈/顺序队列),一个玩链式存储(链栈/链式队列)。
咱先唠栈、再唠队列。
Part1 栈的基本概念
1.1、栈的定义
栈是一种特殊的线性表,特别在哪儿呢?它只允许在固定的一端折腾 —— 要么往里塞数据,要么往外拿数据。能塞能拿的这头叫栈顶,另一头固定不动的叫栈底。
栈里的数据严格遵守 “后进先出”(LIFO,Last In First Out)的规矩,新来的总往栈顶挤,要拿也只能从栈顶拿。
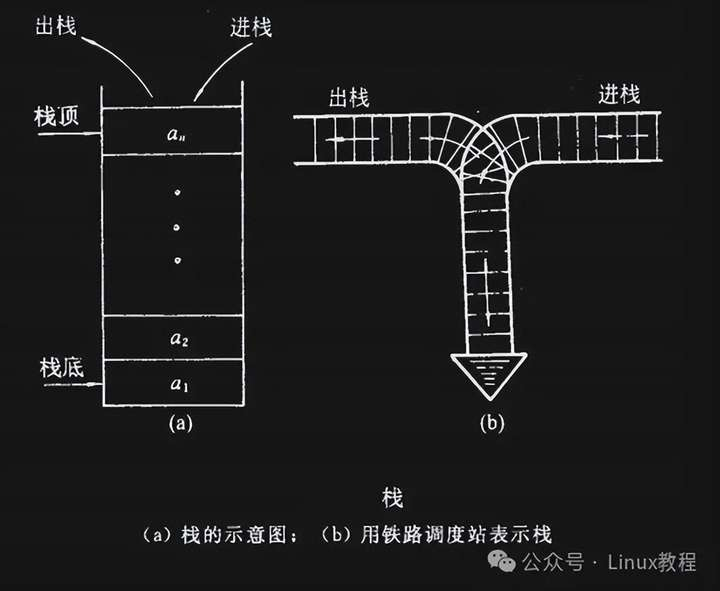
栈的基本操作:
- 压栈(进栈 / 入栈):往栈里加数据,只能从栈顶加,就像往叠好的盘子上再摞一个。
- 出栈:从栈里拿数据,也只能从栈顶拿,就像从最上面拿走一个盘子。
你看,不管是进还是出,都得走栈顶这一个口子,所以 “先进后出” 的原则就这么定死了 —— 先进去的被压在底下,后进去的在上面,拿的时候自然先拿上面的。
栈的六种基本运算:
- 构造空栈(InitStack (S)):初始化一个空栈,啥数据都没有。
- 判栈空(StackEmpty (S)):看看栈里是不是空的,空了就返回 “是”。
- 判栈满(StackFull (S)):检查栈是不是已经塞不下新数据了(这招主要针对顺序栈)。
- 进栈(Push (S,x)):把数据 x 压到栈顶,栈里元素多一个。
- 退栈(Pop (S)):把栈顶的元素删掉并拿出来,栈里元素少一个。
- 取栈顶元素(StackTop (S)):只看栈顶元素是啥,不删它,元素还在栈顶待着。
因为栈也是线性表,所以线性表那套存储结构对它也适用,主要有两种:顺序栈和链栈,存储方式不一样,实现上面这些操作的算法也略有差别。
顺序栈的 “上溢” 和 “下溢”:
顺序栈就像一个固定大小的盒子,比如你用数组实现它,容量是定死的。举个例子,盒子里叠着一摞书,只能从最上面拿(总不能把盒子倒过来吧,那叫耍赖)。
- 上溢:当你往盒子里塞书,塞到超过盒子的容量了,再塞就塞不进去了,这就是上溢 —— 栈顶指针都跑出栈的范围了,明显出错了。
- 下溢:盒子里的书都拿光了,你还想拿,翻来翻去啥也没有,这就是下溢。不过下溢本身能说明栈是空的,所以 often 被用来当程序里的判断条件(比如拿数据前先检查,下溢了就别拿了)。
链栈没那么多讲究:
链栈是用链表实现的,就像一条一头固定的链子,活动的那头就是栈顶。你想加数据,就在栈顶加个新节点;想删数据,就把栈顶节点摘掉。它没有 “上溢” 的烦恼 —— 只要内存够,就能一直加节点,链子能无限变长(理论上哈)。
另外,链栈一般不用加头结点,因为所有操作都在栈顶(也就是链表的头部)进行,加个头结点反而多此一举,还得绕到它后面操作,徒增麻烦。所以直接用链表的头指针指着栈顶就行,简单又高效。
1.2、栈的顺序存储
栈的顺序存储就像用一个固定大小的数组来当 “容器”,所有操作都在数组的一端(栈顶)进行。咱用 C++ 的面向对象风格来封装一下,看看具体咋实现:
#include <iostream>
using namespace std;
#define MAX 10 // 栈的最大容量
class SeqStack { // 顺序栈类
private:int arr[MAX]; // 用数组存栈元素int top; // 栈顶指针(-1表示空栈)
public:// 构造函数:初始化栈SeqStack() {top = -1; // 空栈状态}// 入栈操作void push(int value) {if (top >= MAX - 1) { // 栈满判断(top最大为MAX-1)cout << "栈满了!塞不下啦~" << endl;return;}arr[++top] = value; // 栈顶指针先+1,再存值}// 出栈操作int pop() {if (isEmpty()) { // 栈空判断cout << "栈是空的!没东西可拿~" << endl;return -1; // 用-1表示出错(实际可抛异常)}return arr[top--]; // 先取值,再让栈顶指针-1}// 判断栈是否为空bool isEmpty() {return top == -1; // top=-1就是空栈}
};
// 测试一下
int main() {SeqStack stack;stack.push(3);stack.push(10);stack.push(1);cout << "出栈元素:" << stack.pop() << endl; // 应该输出1return 0;
}结论:顺序栈的好处是操作简单,入栈和出栈不用移动元素(直接操作栈顶指针),但缺点也很明显 —— 容量固定死了,一旦设小了容易满,设大了又浪费空间,想扩容还得手动换个大数组,不够灵活。
其实 Java 里的java.util.Stack也是这么个思路,它继承了Vector(动态数组),在上面加了几个栈专属方法:
- push():入栈(往数组末尾加元素)
- pop():出栈(删末尾元素并返回)
- peek():取栈顶元素(不删除)
- empty():判断是否为空
- search():查找元素位置
举个 Java 使用例子:
import java.util.Stack;
public class StackDemo {public static void main(String[] args) {Stack<Integer> stack = new Stack<>();stack.push(1); // 压栈:[1]stack.push(2); // 压栈:[1,2]stack.push(3); // 压栈:[1,2,3]// 出栈(先进后出)while (!stack.empty()) {System.out.print(stack.pop() + "\t"); // 输出:3 2 1}}
}1.3、栈的链式存储
如果栈里的元素个数不确定(一会儿多一会儿少),顺序栈就不够用了,这时候就得请 “链栈” 出场。链栈用单链表实现,每个节点存一个元素,栈顶就是链表的头,不用头结点,操作起来更方便。
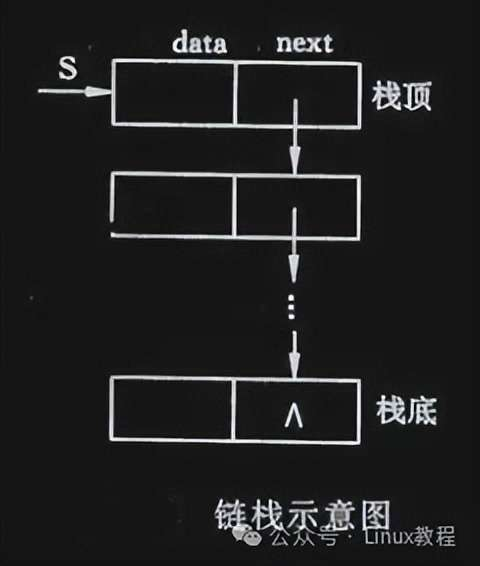
咱用 C 语言简单实现一下链栈的核心操作:
#include <stdio.h>
#include <stdlib.h>
// 定义节点结构
typedef struct Node {int data; // 元素值struct Node* next; // 指向下一个节点
} Node;
// 链栈结构(只需要栈顶指针)
typedef struct {Node* top; // 栈顶指针(指向链表头)
} LinkStack;
// 初始化栈
void initStack(LinkStack* stack) {stack->top = NULL; // 空栈:栈顶为NULL
}
// 入栈(往链表头加节点)
void push(LinkStack* stack, int value) {// 创建新节点Node* newNode = (Node*)malloc(sizeof(Node));if (newNode == NULL) {printf("内存不够啦,入栈失败!\n");return;}newNode->data = value;newNode->next = stack->top; // 新节点指向原来的栈顶stack->top = newNode; // 栈顶指针指向新节点
}
// 出栈(从链表头删节点)
int pop(LinkStack* stack) {if (stack->top == NULL) { // 栈空判断printf("栈是空的,出栈失败!\n");return -1;}Node* temp = stack->top; // 暂存栈顶节点int value = temp->data; // 取栈顶值stack->top = temp->next; // 栈顶指针后移free(temp); // 释放老节点return value;
}
// 测试一下
int main() {LinkStack stack;initStack(&stack);push(&stack, 3);push(&stack, 4);printf("出栈元素:%d\n", pop(&stack)); // 输出4return 0;
}链栈的好处是容量灵活,只要内存够,就能一直加元素,不会有 “栈满” 的烦恼;而且入栈、出栈都是操作链表头,时间复杂度都是 O (1),效率很高。
1.4、栈的应用场景
栈这东西看着简单,用处可不小,咱举几个典型例子:
- 数制转换:比如把十进制转成二进制,除 2 取余法中,余数是倒着输出的 —— 这时候用栈存余数,最后一个个弹出来就是正确的顺序。
- 语法 / 词法分析:写编译器的时候,检查括号是否匹配(比如()、{})就靠栈:遇到左括号压栈,遇到右括号就弹出栈顶,看是否匹配。
- 表达式求值:比如计算3 + (2 * 5) - 4,计算机不好直接算,得先转成后缀表达式(逆波兰式),这个转换过程就得用栈来辅助;求值的时候也得用栈。
除此之外,递归调用的底层实现(函数栈)、浏览器的 “后退” 功能(历史记录存栈里),都离不开栈的 “先进后出” 特性~
1.5、栈与递归:汉诺塔问题的实现
汉诺塔问题是递归思想的经典案例,而栈作为递归的底层实现机制,非常适合用来模拟这一过程。我们先来理解汉诺塔的核心逻辑,再通过栈来实现它。
汉诺塔问题的核心思路
假设有 3 根柱子(X、Y、Z)和 n 个大小不同的盘子(从小到大编号 1~n),初始时所有盘子都在 X 柱上,要求按以下规则移到 Z 柱:

- 每次只能移动 1 个盘子
- 大盘子不能压在小盘子上
解决思路用递归拆解:
- 基础情况
- :如果只有 1 个盘子(n=1),直接从 X 移到 Z。
- 递归情况
- :对于 n 个盘子:
- 先把上面 n-1 个盘子从 X 移到 Y(用 Z 做辅助)
- 把第 n 个盘子从 X 移到 Z
- 最后把 n-1 个盘子从 Y 移到 Z(用 X 做辅助)
基于栈的实现代码
下面用链栈模拟汉诺塔的柱子,并通过递归函数实现移动逻辑:
#include <iostream>
#include <stdlib.h>
using namespace std;// 宏定义状态码
#define TRUE 1
#define FALSE 0
#define OVERFLOW -2 // 内存溢出
#define STACK_EMPTY -3 // 栈空// 链栈节点结构
typedef struct Node {int data; // 存储盘子编号(数字越大盘子越大)struct Node* next; // 指向下一个节点
} Node;// 链栈结构(仅需栈顶指针)
typedef struct {Node* top; // 栈顶指针(指向栈顶节点)
} LinkStack;// 初始化栈
void InitStack(LinkStack& stack) {stack.top = NULL; // 空栈状态
}// 入栈操作
void Push(LinkStack& stack, int value) {Node* newNode = (Node*)malloc(sizeof(Node));if (!newNode) {cerr << "内存分配失败!" << endl;exit(OVERFLOW);}newNode->data = value;newNode->next = stack.top; // 新节点指向原栈顶stack.top = newNode; // 更新栈顶为新节点
}// 出栈操作(返回弹出的值)
int Pop(LinkStack& stack) {if (stack.top == NULL) {cerr << "栈为空,无法出栈!" << endl;exit(STACK_EMPTY);}Node* temp = stack.top; // 暂存栈顶节点int value = temp->data; // 获取栈顶值stack.top = temp->next; // 栈顶指针后移free(temp); // 释放原栈顶节点return value;
}// 打印栈中元素(从栈顶到栈底)
void PrintStack(LinkStack& stack, const string& name) {cout << name << "柱:";Node* p = stack.top;while (p) {cout << p->data << " ";p = p->next;}cout << endl;
}// 移动操作:从from栈弹出元素,压入to栈
void Move(LinkStack& from, LinkStack& to) {int plate = Pop(from);Push(to, plate);
}// 汉诺塔递归函数
// 参数:n-盘子数量,X-源柱,Y-辅助柱,Z-目标柱
void Hanoi(int n, LinkStack& X, LinkStack& Y, LinkStack& Z) {if (n == 1) {Move(X, Z); // 1个盘子直接移到目标柱return;}// 第一步:将n-1个盘子从X移到Y(用Z辅助)Hanoi(n - 1, X, Z, Y);// 第二步:将第n个盘子从X移到ZMove(X, Z);// 第三步:将n-1个盘子从Y移到Z(用X辅助)Hanoi(n - 1, Y, X, Z);
}int main() {LinkStack X, Y, Z; // 三根柱子(栈)InitStack(X);InitStack(Y);InitStack(Z);int n = 3; // 盘子数量(可修改)// 初始化X柱:从大到小放入盘子(栈顶是最小盘)for (int i = n; i >= 1; i--) {Push(X, i);}cout << "初始状态:" << endl;PrintStack(X, "X");PrintStack(Y, "Y");PrintStack(Z, "Z");// 执行汉诺塔移动Hanoi(n, X, Y, Z);cout << "\n移动完成后:" << endl;PrintStack(X, "X");PrintStack(Y, "Y");PrintStack(Z, "Z");return 0;
}代码解析
链栈设计:用LinkStack模拟汉诺塔的柱子,每个栈的top指针指向栈顶(最小的盘子,因为小盘在上面)。
核心操作:
- Push/Pop:实现盘子的入栈(放柱子上)和出栈(从柱子上拿下来)。
- Move:封装从一个栈到另一个栈的移动逻辑(符合汉诺塔规则)。
递归函数Hanoi:严格按照拆解思路实现,通过递归将大问题分解为小问题,直到只剩 1 个盘子。
运行结果(以 n=3 为例)
初始状态:
X柱:1 2 3
Y柱:
Z柱:
移动完成后:
X柱:
Y柱:
Z柱:1 2 3 可以看到,3 个盘子从 X 柱成功移动到了 Z 柱,且保持了从小到大的顺序(栈顶是 1,栈底是 3),符合汉诺塔规则。
Part2 队列
2.1、队列定义
队列(Queue)也是一种受限制的线性表,但它的限制比栈更特殊 —— 两端都有限制:只能在一端插入(队尾),另一端删除(队头)。允许插入的一端叫队头(Front),允许删除的一端叫队尾(Rear)。
队列的核心原则是先进先出(FIFO,First In First Out),就像现实中排队买票:先来的先买,买完先走,后来的只能排后面。
队列的六种基本操作:
- 置空队(InitQueue (Q)):初始化一个空队列。
- 判队空(QueueEmpty (Q)):判断队列是否为空。
- 判队满(QueueFull (Q)):判断队列是否已满(仅顺序队列需要)。
- 入队(EnQueue (Q,x)):在队尾插入元素 x。
- 出队(DeQueue (Q)):删除并返回队头元素。
- 取队头元素(QueueFront (Q)):仅返回队头元素,不删除。
和栈一样,队列也有两种存储结构:顺序队列(用数组实现)和链式队列(用链表实现)。
顺序队列的 “假上溢” 问题
顺序队列用数组存储,通过队头指针(front)和队尾指针(rear)标记队列范围。但这会引出一个坑 ——假上溢:
比如用一个长度为 5 的数组存队列,初始时 front 和 rear 都指向 - 1(空队列)。
- 入队 3 个元素:rear 移动到 2(索引 0、1、2 存元素)。
- 出队 2 个元素:front 移动到 1(只剩索引 2 的元素)。
- 再入队 3 个元素:rear 移动到 5(超出数组长度),但此时数组索引 0、1 其实是空的,却提示 “上溢”—— 这就是假上溢(明明有空位,却因指针越界报错)。
解决办法:循环队列
把数组想象成环形(头尾相接),当指针超出数组最大索引时,自动绕回 0。比如数组长度为 5,rear=4(最后一个索引)时,再入队就让 rear=0。
但循环队列有个新问题:front 和 rear 重合时,既可能是空队列,也可能是满队列。区分方法有三种:
- 用一个布尔变量标记 “空” 或 “满”。
- 故意空出一个数组位置:当 (rear+1)% 数组长度 == front 时,视为满队列。
- 用计数器记录元素个数:等于数组长度时为满,0 时为空。
2.2、队列的顺序存储(循环队列)
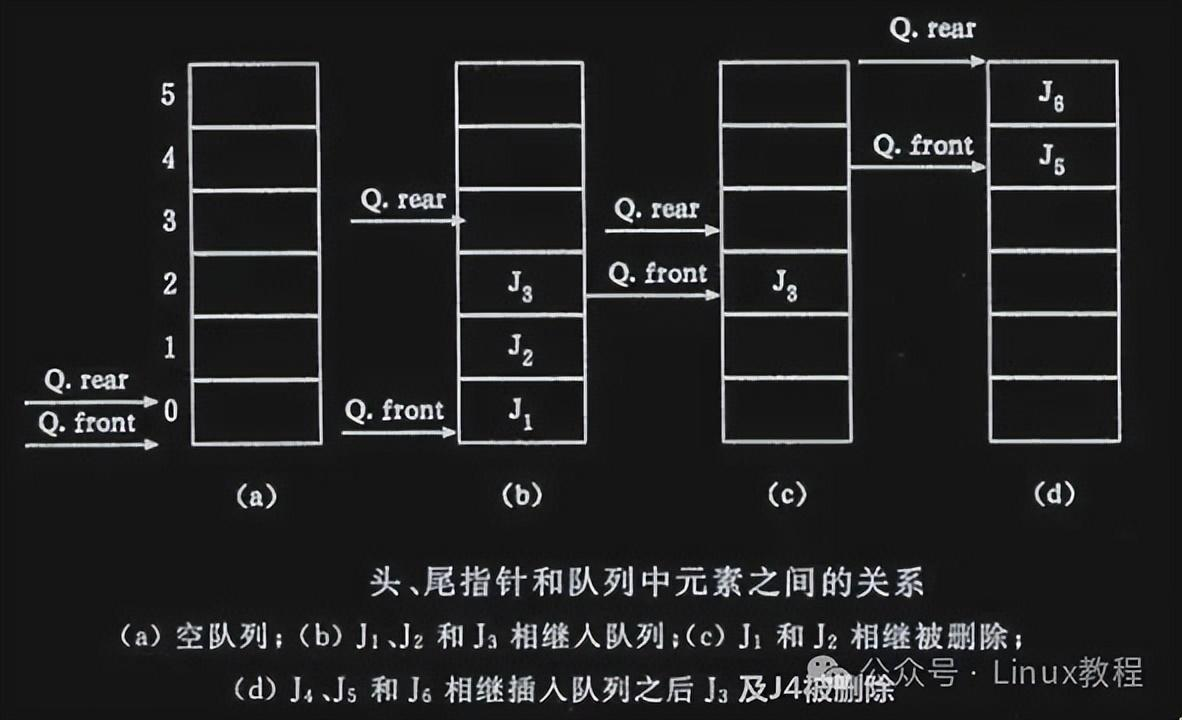
下面用 C 语言实现循环队列(采用 “空出一个位置” 的方式判断满队):
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
#define MAX_QUEUE 10 // 队列最大容量
#define OVERFLOW -2 // 队列满
#define QUEUE_EMPTY -3 // 队列空
// 循环队列结构
typedef struct {int elem[MAX_QUEUE]; // 存储元素的数组int front; // 队头指针(指向队头前一个位置)int rear; // 队尾指针(指向队尾元素)
} CircleQueue;
// 初始化队列
void InitQueue(CircleQueue*& q) {q = (CircleQueue*)malloc(sizeof(CircleQueue));q->front = q->rear = 0; // 初始时首尾指针重合
}
// 入队操作
void EnQueue(CircleQueue* q, int value) {// 检查是否满队:(rear+1)绕一圈后等于frontif ((q->rear + 1) % MAX_QUEUE == q->front) {cerr << "队列满了!" << endl;exit(OVERFLOW);}q->rear = (q->rear + 1) % MAX_QUEUE; // 队尾指针后移(绕圈)q->elem[q->rear] = value; // 存入元素
}
// 出队操作
int DeQueue(CircleQueue* q) {if (q->front == q->rear) { // 队空判断cerr << "队列为空!" << endl;exit(QUEUE_EMPTY);}q->front = (q->front + 1) % MAX_QUEUE; // 队头指针后移(绕圈)return q->elem[q->front]; // 返回队头元素
}
// 测试
int main() {CircleQueue* q;InitQueue(q);EnQueue(q, 1);EnQueue(q, 2);cout << "出队元素:" << DeQueue(q) << endl; // 输出1return 0;
}注意:顺序队列的容量固定,若无法预估最大长度,建议用链式队列。
2.3、链式队列
链式队列用单链表实现,队头指针(front)指向头结点,队尾指针(rear)指向最后一个元素。好处是容量灵活,无需担心溢出。
C 语言实现:
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
// 节点结构
typedef struct Node {int data; // 元素值struct Node* next; // 指向下一节点
} Node;
// 链式队列结构
typedef struct {Node* front; // 队头指针(指向头结点)Node* rear; // 队尾指针(指向最后一个元素)
} LinkQueue;
// 初始化队列(带头结点,方便操作)
void InitQueue(LinkQueue* q) {q->front = q->rear = (Node*)malloc(sizeof(Node));q->front->next = NULL; // 头结点.next初始为NULL
}
// 入队操作(在队尾加节点)
void EnQueue(LinkQueue* q, int value) {Node* newNode = (Node*)malloc(sizeof(Node));newNode->data = value;newNode->next = NULL;q->rear->next = newNode; // 原队尾节点指向新节点q->rear = newNode; // 更新队尾指针
}
// 出队操作(删除队头节点)
int DeQueue(LinkQueue* q) {if (q->front == q->rear) { // 队空判断(头结点后无元素)cerr << "队列为空!" << endl;exit(-1);}Node* temp = q->front->next; // 暂存队头元素节点int value = temp->data;q->front->next = temp->next; // 头结点指向新队头// 如果删除的是最后一个元素,队尾指针也要指向头结点if (q->rear == temp) {q->rear = q->front;}free(temp);return value;
}
// 测试
int main() {LinkQueue q;InitQueue(&q);EnQueue(&q, 1);EnQueue(&q, 2);cout << "出队元素:" << DeQueue(&q) << endl; // 输出1return 0;
}2.4、队列的应用场景
队列的 “先进先出” 特性在很多场景中都能派上用场:
- 银行排队系统:客户按到达顺序排队,窗口按顺序叫号,符合 FIFO 原则。
- 打印机缓冲区:主机快速向缓冲区写入数据(入队),打印机缓慢从缓冲区读取(出队),解决速度不匹配问题,提高主机效率。
- CPU 分时系统:多个程序请求使用 CPU 时,按请求顺序排成队列,CPU 轮流为每个程序分配时间片,保证公平性。
- 广度优先搜索(BFS):遍历树或图时,用队列存储待访问节点,按层次顺序访问,典型应用如 “最短路径” 求解。
- 消息队列:分布式系统中,用队列暂存消息,避免发送方和接收方直接耦合,实现异步通信。
队列的核心价值在于 “有序排队”,让数据或任务按顺序处理,避免混乱。
Part3 栈和队列的区别
以下是栈和队列的详细对比分析,从核心定义、操作特性到具体实现方式,帮助你全面理解它们的区别:
3.1、核心定义与特性:一个 “后进先出”,一个 “先进先出”
| 特性 | 栈(Stack) | 队列(Queue) |
| 定义 | 只允许在栈顶(表尾)插删,遵循 后进先出(LIFO) | 队尾插、队头删,遵循 先进先出(FIFO) |
| 操作限制 | 所有操作(入栈、出栈)都在栈顶这一个 “口子” 进行 | 入队在队尾、出队在队头,两头分工明确 |
| 典型场景 | 适合“后处理先完成”的场景,如撤销操作、函数调用栈、表达式求值、括号匹配。 | 适合“先处理先完成”的场景,如任务调度、消息缓冲、广度优先搜索(BFS)、打印队列。 |
3.2、操作对比
| 操作 | 栈 | 队列 |
| 插入位置 | 栈顶(表尾),新元素直接 “叠” 在最上面,成为新栈顶 | 队尾,新元素 “排” 在最后,乖乖等前面的处理完 |
| 删除位置 | 栈顶,每次删的都是最后插进去的元素(LIFO 的体现) | 队头,每次删的都是最早插进去的元素(FIFO 的体现) |
| 核心操作 |
|
|
| 时间复杂度 | 所有操作都是 O (1)(只动栈顶指针,不用挪元素) | 所有操作都是 O (1)(只动队头 / 队尾指针) |
3.3、数据结构实现:存储方式各有讲究
1)、栈的实现:两种方式都简单
- 顺序栈(数组实现):
用一个数组存元素,top指针标记栈顶位置(初始 - 1 表示空栈)。入栈时top++再存值,出栈时取值再top--。
✨ 优化技巧:可以用一个数组实现 “两栈共享空间”(数组两端各当一个栈底),省内存。 - 链栈(链表实现):
不用头结点,链表头就是栈顶。入栈 = 头插法(新节点放最前),出栈 = 删头节点。好处是没容量限制(内存够就行)。
2)、队列的实现:得解决 “假溢出” 问题
- 顺序队列(循环队列)(数组实现):用front(队头前一个位置)和rear(队尾)两个指针管理。为了避免 “假溢出”(数组没满但指针越界),把数组想象成环形,指针超界时绕回开头(用%运算实现)。
- 队满判断:(rear + 1) % 数组长度 == front(故意空一个位置,区分空和满)。
- 链队列(链表实现):带头结点(方便操作),front指表头,rear指最后一个元素。入队 = 尾插法(新节点接在rear后面),出队 = 删表头的下一个节点。同样没容量限制。
3.4、结构示意图:直观感受差异
- 栈:就一个 “出入口”(栈顶),元素像叠盘子
栈顶 → [元素3] ← 新元素从这进,也从这出[元素2][元素1]
栈底 → [栈底] ← 固定不动队列:两个 “口”(队头进,队尾出),元素像排队
队头 → [元素1] ← 从这出(最早来的先出)[元素2]
队尾 → [元素3] ← 从这进(新来的排最后)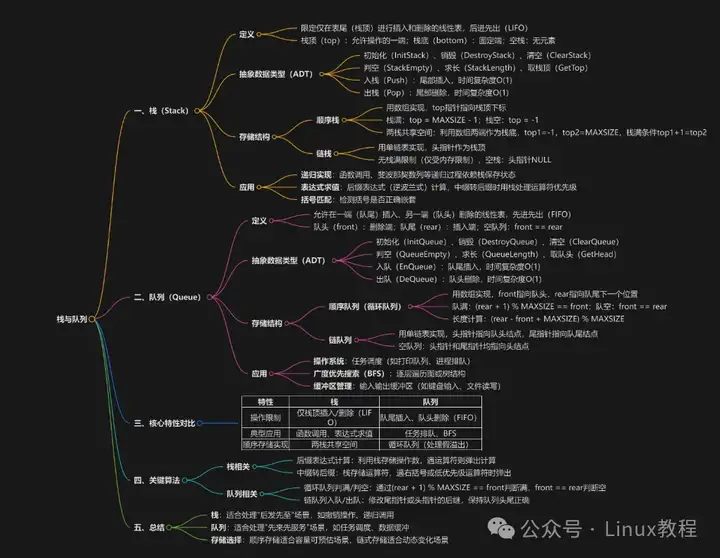
往期推荐
【大厂标准】Linux C/C++ 后端进阶学习路线
解构内存池:C++高性能编程的底层密码
知识点精讲:深入理解C/C++指针
总被 “算法” 难住?程序员怎样学好算法?
小米C++校招二面:epoll和poll还有select区别,底层方式?
顺时针螺旋移动法 | 彻底弄懂复杂C/C++嵌套声明、const常量声明!!!
C++ 基于原子操作实现高并发跳表结构
为什么很多人劝退学 C++,但大厂核心岗位还是要 C++?
手撕线程池:C++程序员的能力试金石
打破认知:Linux管道到底有多快?
C++的三种参数传递机制:从底层原理到实战
顺时针螺旋移动法 | 彻底弄懂复杂C/C++嵌套声明、const常量声明!!!
阿里面试官:千万级订单表新增字段,你会怎么弄?
C++内存模型实例解析
字节跳动2面:为了性能,你会牺牲数据库三范式吗?
字节C++一面:enum和enum class的区别?
Redis分布式锁:C++高并发开发的必修课
C++内存对齐:从实例看结构体大小的玄机
