【代码随想录算法训练营——Day15】二叉树——110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和、222.完全二叉树的节点个数

LeetCode题目链接
https://leetcode.cn/problems/balanced-binary-tree/
https://leetcode.cn/problems/binary-tree-paths/
https://leetcode.cn/problems/sum-of-left-leaves/
https://leetcode.cn/problems/count-complete-tree-nodes/

题解
110.平衡二叉树

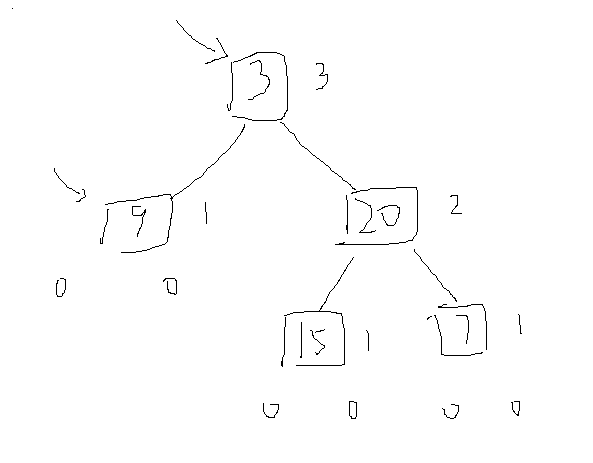
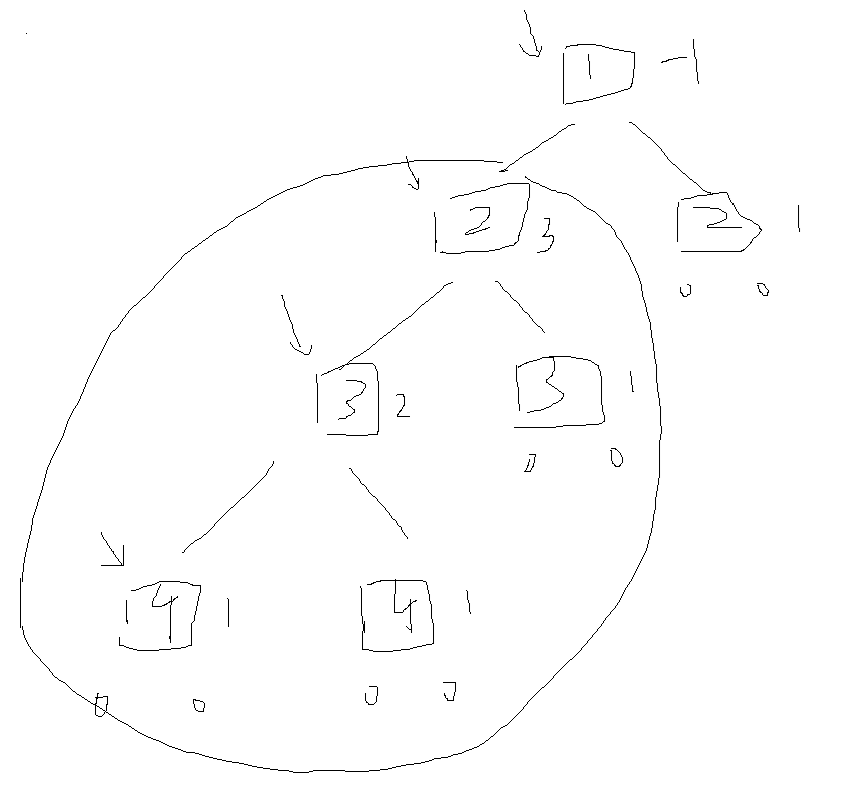
想到用左子树的高度减右子树的高度，但递归不知道怎么求高度。在求高度的函数里，高度depth放在条件里还是在函数体里重新定义一个变量。用层序遍历求高度行不行？不用递归？
看了题解，首先明确递归终止条件，遇到空结点时高度为0。接着递归得到左右子树的高度，并确定一个规则，就是当遇到的树不是平衡树时，返回-1。但对高度判断的条件又怎么写呢？直接判断是否等于-1。在后面计算result值时，要把当前结点的高度也加上，左右子树的高度的最大值。
通过空结点传回的高度为0确定整棵树的高度基点，然后往上返回时都能令符合平衡二叉树结点的”根“结点高度值加1，当某个结点不满足平衡二叉树的要求时，它以及它上面的所有结点高度值都将为-1。-1是个标记，标记本树中出现了不符合平衡二叉树的子树。

257.二叉树的所有路径
知道用回溯的方法写这道题，但不知道怎么放每次的递归条件。答案是当前的路径（因为要回溯）和结果数组（题目要求string）。
自己顺着思路写了一遍代码，小case过了，最后也过了。

404.左叶子之和
想到用递归去做，但是每次判断左叶子的条件不知道怎么定，还有一个思路是对每个左结点打标记，但怎么区分左叶子结点和左普通结点。
于是看题解，从左叶子结点的父结点去判断该结点是否是左叶子结点，这个思路其实我想到了，但一开始觉得麻烦，就没定下来。递归边界要确定，返回的是左叶子结点的值。后续的递归分支写法和110.平衡二叉树很像，但要注意求了赋值了两次同一个值，原因是左子树的值如果求出来了，而左叶子结点如果递归了返回的是0，这时需要在当前判断求左叶子结点的值，并重新赋值覆盖前面的。
有一个录友说，第一个是递归过程，第二个是真的在求叶子结点的值。

222.完全二叉树的节点个数
这一题是我唯一会的一题，用迭代法，任何一种遍历顺序都可以，但用递归法。写成了求叶子结点个数的代码，改了一下要加上当前结点的个数。看了一下题解，跟我写的也差不多。

代码

//110.平衡二叉树
#include <iostream>
using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isBalanced(TreeNode* root) {int depth = getHeight(root);if (depth == -1) return false;else return true;}int getHeight(TreeNode* root) {if (root == NULL) return 0;int leftHeight = getHeight(root->left);int rightHeight = getHeight(root->right);if (leftHeight == -1) return -1;if (rightHeight == -1) return -1;if (abs(leftHeight - rightHeight) > 1)return -1;else return 1 + max(leftHeight, rightHeight);}
};int main() {int nums1[30] = { 3,9,20,NULL,NULL,15,7 }, nums2[30] = { 1,2,2,3,3,NULL,NULL,4,4 };TreeNode* root1 = new TreeNode(3);root1->left = new TreeNode(9);root1->right = new TreeNode(20);root1->right->left = new TreeNode(15);root1->right->right = new TreeNode(7);TreeNode* root2 = new TreeNode(1);root2->left = new TreeNode(2);root2->right = new TreeNode(2);root2->left->left = new TreeNode(3);root2->left->right = new TreeNode(3);root2->left->left->left = new TreeNode(4);root2->left->left->right = new TreeNode(4);Solution s;printf("%d", s.isBalanced(root2));return 0;
}

//257.二叉树的所有路径
#include <iostream>
#include <vector>
#include <string>
using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (root == NULL) return result;path.push_back(root->val);travelsal(root, path, result);return result;}void travelsal(TreeNode* cur, vector<int> &path, vector<string> &result) {if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0;i < path.size() - 1;i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);}if (cur->left) {path.push_back(cur->left->val);travelsal(cur->left, path, result);path.pop_back();}if (cur->right) {path.push_back(cur->right->val);travelsal(cur->right, path, result);path.pop_back();}}
};int main() {int nums1[30] = { 1,2,3,NULL,5 }, nums2[30] = { 1 };TreeNode* root1 = new TreeNode(1);root1->left = new TreeNode(2);root1->right = new TreeNode(3);root1->left->right = new TreeNode(5);TreeNode* root2 = new TreeNode(1);Solution s;vector<string> result = s.binaryTreePaths(root2);for (int i = 0;i < result.size();i++) {cout << result[i] << " " << endl;}return 0;
}

//404.左叶子之和
#include <iostream>
using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right == NULL) return 0;int leftValue = sumOfLeftLeaves(root->left);if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right);return leftValue + rightValue;}
};int main() {int nums1[30] = { 3,9,20,NULL,NULL,15,7 }, nums2[30] = { 1 };TreeNode* root1 = new TreeNode(3);root1->left = new TreeNode(9);root1->right = new TreeNode(20);root1->right->left = new TreeNode(15);root1->right->right = new TreeNode(7);TreeNode* root2 = new TreeNode(1);Solution s;printf("%d", s.sumOfLeftLeaves(root2));return 0;
}

//222.完全二叉树的节点个数
#include <iostream>
using namespace std;struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int countNodes(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right == NULL) return 1;int leftNum = countNodes(root->left);int rightNum = countNodes(root->right);return leftNum + rightNum + 1;}
};int main() {int nums1[30] = { 1,2,3,4,5,6 }, nums2[30] = {}, nums3[30] = {1};TreeNode* root1 = new TreeNode(1);root1->left = new TreeNode(2);root1->right = new TreeNode(3);root1->left->left = new TreeNode(4);root1->left->right = new TreeNode(5);root1->right->left = new TreeNode(6);TreeNode* root2 = nullptr;TreeNode* root3 = new TreeNode(1);Solution s;printf("%d", s.countNodes(root3));return 0;
}