C#实现WGS-84到西安80坐标系转换的完整指南
C#实现WGS-84到西安80坐标系转换的完整指南
坐标转换是GIS和测绘领域的核心技术之一,不同的坐标系之间转换需要精确的数学模型和参数。本文将详细解析一个使用C#实现的WGS-84到西安80坐标系转换程序,从理论基础到代码实现进行全面讲解。
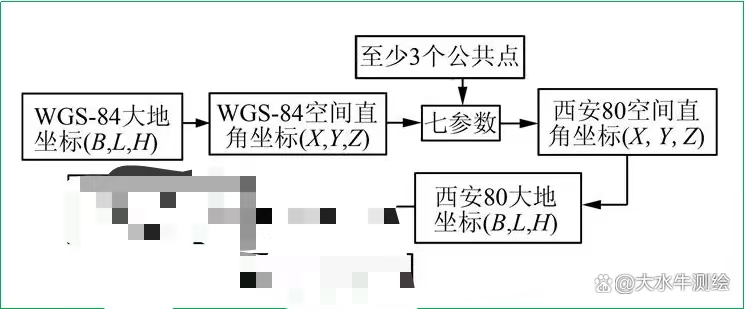
坐标系基础
WGS-84坐标系
WGS-84(World Geodetic System 1984)是全球定位系统(GPS)使用的标准坐标系。它是一个地心坐标系,以地球质心为原点,Z轴指向国际时间局(BIH)1984.0定义的协议地球极(CTP)方向,X轴指向BIH 1984.0的零子午面和CTP赤道的交点,Y轴与X、Z轴构成右手坐标系。
西安80坐标系
西安80坐标系是中国自1980年开始使用的大地坐标系,属于参心坐标系。它采用1975年国际大地测量与地球物理联合会(IUGG)推荐的IAG 75椭球参数,椭球短轴平行于由地球质心指向地极原点的方向。
转换原理
大地坐标与空间直角坐标的相互转换
大地坐标(B, L, H) → 空间直角坐标(X, Y, Z)
转换公式为:
X = (N + H) * cos(B) * cos(L) Y = (N + H) * cos(B) * sin(L) Z = [N * (1 - e²) + H] * sin(B)
其中N为卯酉圈曲率半径:
N = a / √(1 - e² * sin²(B))
e²为第一偏心率的平方:
e² = (a² - b²) / a²
空间直角坐标(X, Y, Z) → 大地坐标(B, L, H)
这是一个迭代计算过程:
计算经度L:
L = atan(Y / X)初始化纬度B:
B = atan(Z / √(X² + Y²))迭代计算直到收敛:
N = a / √(1 - e² * sin²(B)) H = √(X² + Y²) / cos(B) - N B = atan(Z / (√(X² + Y²) * (1 - e² * N / (N + H))))
七参数转换模型
七参数转换模型用于在不同空间直角坐标系之间进行转换,包括:
3个平移参数(ΔX, ΔY, ΔZ)
3个旋转参数(εx, εy, εz)
1个尺度变化参数(m)
转换公式为:
[X₂] [ΔX] [1 εz -εy] [X₁] [Y₂] = [ΔY] + (1+m) * [-εz 1 εx] [Y₁] [Z₂] [ΔZ] [εy -εx 1 ] [Z₁]
程序实现详解
1. 数据结构设计
程序定义了两种数据结构来存储不同类型的坐标:
// 存储大地坐标(B, L, H)
public class dataJS {public string name { get; set; } // 点名称public double x { get; set; } // 经度或X坐标public double y { get; set; } // 纬度或Y坐标public double h { get; set; } // 高程
}// 存储空间直角坐标(X, Y, Z)
public class dataJSXYZ {public string name { get; set; } // 点名称public double x { get; set; } // X坐标public double y { get; set; } // Y坐标public double z { get; set; } // Z坐标
}2. 椭球参数定义
程序定义了WGS-84和西安80两种椭球的参数:
// WGS-84椭球体常数 private const double a = 6378137.0; // 长半轴(米) private const double b = 6356752.3142; // 短半轴(米) private const double f = 1 / 298.257223563; // 扁率 private const double e2 = (a*a - b*b)/(a*a); // 第一偏心率的平方// 西安80椭球体常数 private const double a_xa80 = 6378140.0; // 长半轴(米) private const double b_xa80 = 6356755.2882; // 短半轴(米) private const double f_xa80 = 1 / 298.257; // 扁率 private const double e2_xa80 = (a_xa80*a_xa80 - b_xa80*b_xa80)/(a_xa80*a_xa80);
3. 核心转换函数
大地坐标转空间直角坐标
public static (double X, double Y, double Z) ConvertToEcef(double B, double L, double H)
{// 将角度转换为弧度L = L * Math.PI / 180; // 经度转弧度B = B * Math.PI / 180; // 纬度转弧度// 计算曲率半径Ndouble N = a / Math.Sqrt(1 - e2 * Math.Sin(B) * Math.Sin(B));// 计算空间直角坐标double X = (N + H) * Math.Cos(B) * Math.Cos(L);double Y = (N + H) * Math.Cos(B) * Math.Sin(L);double Z = ((1 - e2) * N + H) * Math.Sin(B);return (X, Y, Z);
}七参数转换

public static void WGS84ToXiAn80(double X, double Y, double Z,double Tx, double Ty, double Tz,double Rx, double Ry, double Rz,double S, out double Xp, out double Yp, out double Zp)
{// 角度转换:旋转参数Rx, Ry, Rz通常是角秒,需要转换为弧度double Rx_rad = Rx * Math.PI / (180 * 3600);double Ry_rad = Ry * Math.PI / (180 * 3600);double Rz_rad = Rz * Math.PI / (180 * 3600);// 七参数转换公式Xp = Tx + X * (1 + S) + Y * Rz_rad - Z * Ry_rad;Yp = Ty - X * Rz_rad + Y * (1 + S) + Z * Rx_rad;Zp = Tz + X * Ry_rad - Y * Rx_rad + Z * (1 + S);
}空间直角坐标转大地坐标
public static void ConvertXYZToBLH(double X, double Y, double Z, out double B, out double L, out double H)
{// 计算经度LL = Math.Atan2(Y, X) * 180 / Math.PI;// 计算辅助变量double p = Math.Sqrt(X * X + Y * Y);double theta = Math.Atan2(Z * a_xa80, p * b_xa80);// 计算纬度BB = Math.Atan2(Z + e21_xa80 * b_xa80 * Math.Pow(Math.Sin(theta), 3),p - e2_xa80 * a_xa80 * Math.Pow(Math.Cos(theta), 3));B = B * 180 / Math.PI;// 计算高程Hdouble N = a_xa80 / Math.Sqrt(1 - e2_xa80 * Math.Pow(Math.Sin(B * Math.PI / 180), 2));H = p / Math.Cos(B * Math.PI / 180) - N;
}4. 七参数计算
七参数的计算需要至少3个公共点(在两个坐标系中都知道坐标的点)。程序中使用最小二乘法计算七参数:
public static TransformationParameters CalculateTransformationParameters(double[,] sourcePoints, double[,] targetPoints)
{int numPoints = sourcePoints.GetLength(0);// 构建设计矩阵A和观测值矩阵LMatrix<double> A = Matrix<double>.Build.Dense(3 * numPoints, 7);Matrix<double> L = Matrix<double>.Build.Dense(3 * numPoints, 1);for (int i = 0; i < numPoints; i++){double X = sourcePoints[i, 0];double Y = sourcePoints[i, 1];double Z = sourcePoints[i, 2];double Xp = targetPoints[i, 0];double Yp = targetPoints[i, 1];double Zp = targetPoints[i, 2];// 填充设计矩阵AA[3 * i, 0] = 1; A[3 * i, 1] = 0; A[3 * i, 2] = 0;A[3 * i, 3] = 0; A[3 * i, 4] = -Z; A[3 * i, 5] = Y; A[3 * i, 6] = X;A[3 * i + 1, 0] = 0; A[3 * i + 1, 1] = 1; A[3 * i + 1, 2] = 0;A[3 * i + 1, 3] = Z; A[3 * i + 1, 4] = 0; A[3 * i + 1, 5] = -X; A[3 * i + 1, 6] = Y;A[3 * i + 2, 0] = 0; A[3 * i + 2, 1] = 0; A[3 * i + 2, 2] = 1;A[3 * i + 2, 3] = -Y; A[3 * i + 2, 4] = X; A[3 * i + 2, 5] = 0; A[3 * i + 2, 6] = Z;// 填充观测值矩阵LL[3 * i, 0] = Xp - X;L[3 * i + 1, 0] = Yp - Y;L[3 * i + 2, 0] = Zp - Z;}// 使用最小二乘法求解参数:X = (A^T * A)^(-1) * A^T * LMatrix<double> AT = A.Transpose();Matrix<double> ATA = AT * A;Matrix<double> ATL = AT * L;Matrix<double> X = ATA.Inverse() * ATL;// 提取七参数return new TransformationParameters{Tx = X[0, 0],Ty = X[1, 0],Tz = X[2, 0],Rx = X[3, 0],Ry = X[4, 0],Rz = X[5, 0],S = X[6, 0]};
}5. 文件操作
程序提供了文件读取和写入功能:
// 读取文件
private List<string> ReadData()
{List<string> lines = new List<string>();OpenFileDialog openFileDialog = new OpenFileDialog{Filter = "Text Files (*.txt)|*.txt|All Files (*.*)|*.*",Title = "选择坐标文件"};if (openFileDialog.ShowDialog() == DialogResult.OK){try{using (StreamReader reader = new StreamReader(openFileDialog.FileName)){string line;while ((line = reader.ReadLine()) != null){lines.Add(line);}}}catch (Exception ex){MessageBox.Show($"读取文件时发生错误: {ex.Message}");}}return lines;
}// 写入文件
private void WriteData(List<string> dataList)
{try{using (StreamWriter writer = new StreamWriter(resultPath)){foreach (string line in dataList){writer.WriteLine(line);}}MessageBox.Show("文件已成功保存到: " + resultPath);}catch (Exception ex){MessageBox.Show($"写入文件时发生错误: {ex.Message}");}
}使用指南
1. 准备输入数据
创建一个文本文件,每行包含一个点的数据,格式为:
点名,经度,纬度,高程
例如:
Point1,116.391,39.907,50 Point2,116.392,39.908,50 Point3,116.393,39.909,50
2. 设置七参数计算点
在程序界面中,输入三个已知点在两个坐标系中的坐标:
WGS-84坐标系下的空间直角坐标(通过ConvertToEcef函数计算得到)
西安80坐标系下的空间直角坐标(已知值)
3. 执行转换
点击"导入"按钮,选择准备好的数据文件,程序将自动完成以下步骤:
读取WGS-84大地坐标
转换为WGS-84空间直角坐标
使用七参数转换为西安80空间直角坐标
转换为西安80大地坐标
保存结果到文件
4. 查看结果
转换结果将保存到程序所在目录的"result.txt"文件中,格式与输入文件相同。
注意事项
精度问题:坐标转换涉及复杂的数学计算,精度受多种因素影响,包括参数精度、计算方法和迭代次数等。
七参数获取:七参数的准确性直接影响转换结果。在实际应用中,应通过专业测量获取准确的七参数。
适用范围:七参数转换模型通常适用于小范围区域(一般不超过150公里×150公里)。对于大范围区域,应考虑使用更复杂的转换模型。
椭球参数:确保使用正确的椭球参数,不同坐标系使用不同的椭球参数。
单位转换:注意角度单位(度/弧度)和长度单位(米)的转换。
扩展与优化
增加图形界面:可以添加数据可视化功能,显示转换前后的坐标点分布。
支持更多坐标系:扩展程序以支持更多坐标系之间的转换,如北京54、CGCS2000等。
批量处理:优化算法以提高大批量数据处理的效率。
参数优化:添加参数优化功能,通过更多公共点提高七参数的准确性。
误差分析:添加转换误差分析和评估功能。
结语
本文详细介绍了WGS-84到西安80坐标系转换的原理和C#实现方法。通过这个程序,您可以理解坐标转换的基本原理和实现过程。在实际应用中,应根据具体需求选择合适的转换模型和参数,并进行充分的精度验证。
坐标转换是一个复杂的过程,需要综合考虑多种因素。希望本文能为您的坐标转换工作提供有益的参考和帮助。
