牛客：校门外的树

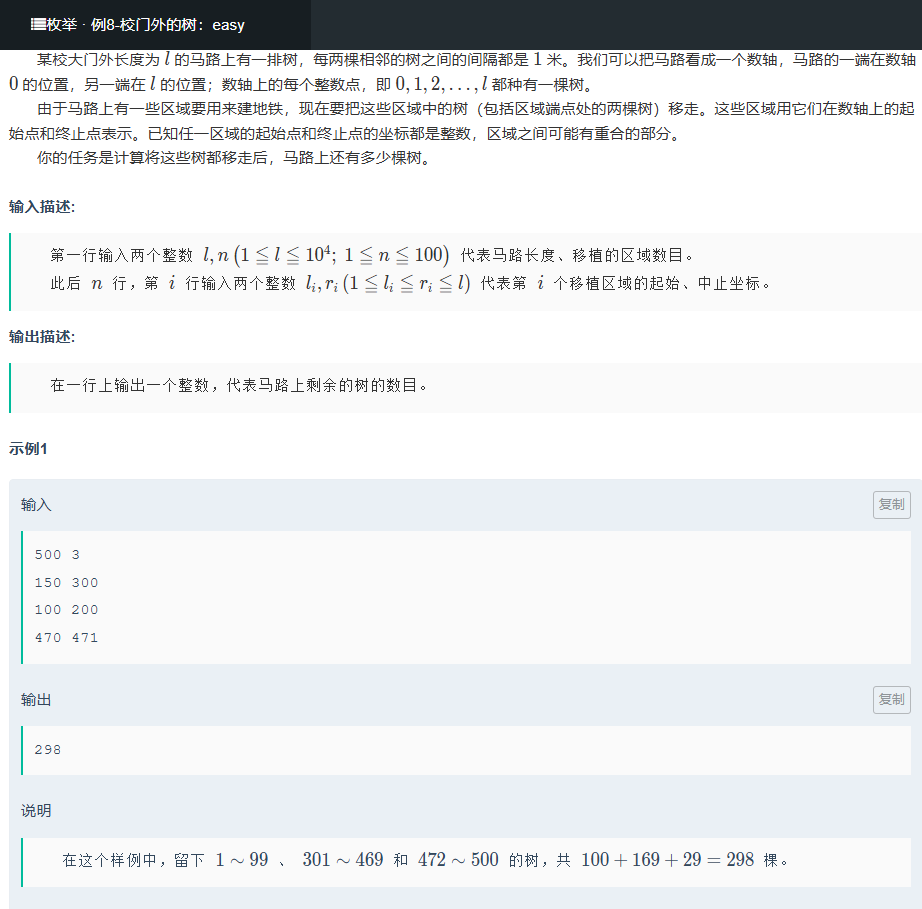
这道题的核心是计算移除指定区间内的树后，剩余的树的数量。代码使用差分法高效解决了区间覆盖问题，时间复杂度为 O (L + n)，比暴力遍历更优。

差分解题思路：

1. 问题分析：

   • 马路被视为数轴 [0, L]，每个整数点都有一棵树，初始共有 L+1 棵树
   • 需要移除 n 个区间内的所有树（包括端点）
   • 目标是计算剩余树的数量

2. 差分法原理：

   • 使用数组vis标记区间的覆盖情况
   • 对于每个移除区间 [l, r]：
     • vis[l]++：标记区间开始
     • vis[r+1]--：标记区间结束的下一个位置
   • 通过累加vis数组得到每个位置被覆盖的次数

3. 计算剩余树：

   • 遍历 [0, L] 区间，累加vis数组得到a（当前位置被覆盖的次数）
   • 当a == 0时，表示该位置的树未被移除，计数器cnt加 1
   • 最终cnt即为剩余树的数量

#include<bits/stdc++.h>
using namespace std;
int main(){int vis[10010]={0};int L,n,l,r;cin>>L>>n;for(int i=0;i<n;i++){cin>>l>>r;if(l>r) swap(l,r);vis[l]++;vis[r+1]--;}int a=0;int cnt=0;for(int i=0;i<=L;i++){a+=vis[i];if(a==0) cnt++;}cout<<cnt;return 0;
}

区间合并法思路：

1. 计算初始总树数：马路范围为 0 到 L（含两端），共 L+1 棵树。
2. 处理移除区间：
   • 将所有需移除树的区间按起点从小到大排序。
   • 合并重叠或相邻的区间（若后一区间起点 ≤ 当前区间终点，则合并为更大的区间）。
3. 计算移除总数：对合并后的每个区间，计算其包含的树的数量（区间长度 + 1），累加得到需移除的总树数。
4. 求剩余树数：用初始总树数减去移除总数，即为结果。

#include<bits/stdc++.h>
using namespace std;
struct pos{int x;int y;
}vis[1000];bool comp(pos a,pos b){if(a.x<b.x) return true; return false;
}
int main(){int L,n,l,r;cin>>L>>n;int cnt=L+1;for(int i=0;i<n;i++){cin>>l>>r;if(l>r) swap(l,r);vis[i].x=l;vis[i].y=r;}sort(vis,vis+n,comp);int l1=vis[0].x,r1=vis[0].y;for(int i=1;i<n;i++){if(r1>vis[i].x){r1=max(vis[i].y,r1);}else{cnt-=(r1-l1+1);l1=vis[i].x;r1=vis[i].y;}}cnt-=(r1-l1+1);cout<<cnt<<endl; return 0;
}