WWW‘25一通读 |图Anomaly/OOD检测相关文章（1）

写在前面：进入新一轮学习阶段，从阅读开始。
本文分享的是WWW2025收录的与作者研究相近的graph-based xx相关paper的阅读笔记，含个人理解，仅供参考😄

0x01 HEI：利用不变性原理实现异配图结构分布偏移学习

Jinluan Yang, et al. Leveraging Invariant Principle for Heterophilic Graph Structure.（浙大）

1.1 摘要

异配图神经网络（Heterophilic graph neural networks, HGNNs）在图的半监督学习任务中表现出了良好的效果。值得注意的是，大多数现实世界中的异配图是由不同邻接模式的节点混合而成的，呈现出局部节点级别的同配（Homophilic）和异配结构。

然而，现有的研究仅致力于设计更好的统一的HGNN架构，以同时用于异配和同配图上的节点分类任务，弄且它们对HGNN性能关于节点的分析仅基于已确定的数据分布，而没有探索由于训练节点和测试节点的结构模式差异所导致的影响。如何在异配图上学习不变的节点表示以处理这种结构差异活分布变化仍未得到探索。

在本文中，我们首先从数据增强的角度讨论了以往基于图的不变学习方法在解决异配图结构分布偏移的局限性。
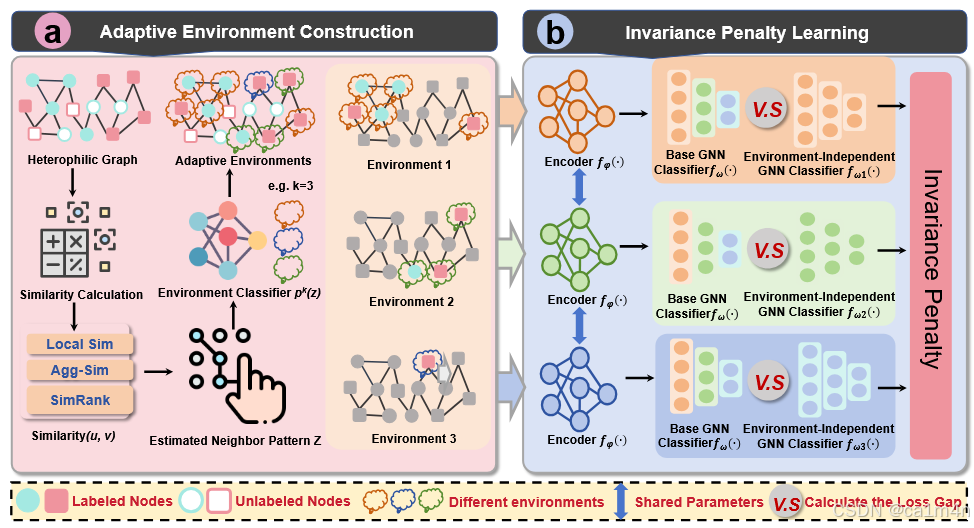
然后，我们提出了HEI这一框架，它能够通过整合异配信息（即节点的估计邻接模式）来生成不变的节点表示，从而在无需扩充数据的情况下推断出潜在环境，并用于不变性预测。
我们提供了详细的理论保证以阐明HEI的合理性。在各种基准测试和骨干网络上的大量实验也表明，与现有的SOTA基线相比，我们的方法具有有效性和鲁棒性。

开源代码：HEI

1.2 背景与动机

异配图结构分布偏移（Heterophilic Graph Structure distribution Shift, HGSS）：一种全新的数据分布偏移视角，用于重新审视现有的HGNNs工作。

尽管前景可观，但大多数先前的HGNNs假设节点共享已确定的数据分布，我们认为不同邻接模式的节点之间存在数据分布差异。如图1（a1）所示，异配图由具有局部同配性和异配性结构的节点混合组成，即节点具有不同的邻接模式。节点的邻接模式可以通过节点同配性来衡量，通过比较节点与其邻接节点的标签来表示同配水平。在此，我们将训练节点和测试节点之间不同的邻接模式识别为异配图结构分布偏移（图1（a2））。这种偏移在先前的工作中被忽视，但实际上影响了GNN的性能。如图1（a3）所示，我们在Squirrel数据集上可视化了训练节点和测试节点之间的HGSS。与测试节点相比，训练节点更倾向于高同配性，这可能导致测试性能下降。
值得注意的是，尽管一些近期的研究也探讨了同配和异配结构模式，但到目前为止，它们尚未为这一问题提供明确的技术解决方案。与专注于backbone设计的传统HGNN研究相比，从数据分布的角度寻求解决方案以解决HGSS问题显得尤为迫切。

现有基于图的不变性学习（Invariant learning）方法由于采用了基于扩充的环境构建策略，在处理HGSS问题时表现不佳。
在一般分布变化的背景下，不变性学习技术因其在减轻这方面的有效性越来越受到认可。其基本方法是学习节点表示，以促进在各种构建环境中进行不变性预测器的学习（图1（b1）），遵循风险外推（Risk Extrapolation, REx）原则。不幸的是，之前的基于图的不变学习方法可能无法有效地解决HGSS问题，主要是因为明确的环境可能对不变性学习无效。如（图1（c1））所示，在HGSS设置中，改变原始结构并不总是能影响节点的邻接模式。实际上，获得与邻域模式相关的最优且多样的环境是具有挑战性的。我们的观察（图1（c2））表明，EERM，一种利用环境扩充来解决节点级任务中的图分布变化的开创性不变性学习方法，在HGSS设置下表现不佳。有时，其改进效果还不如直接采用原始的V-Rex方法，后者是通过将训练节点随机分布在不同的环境组中实现的。我们将这种现象归因于不合理的环境构建。根据我们的分析，EERM实质上是V-Rex的节点环境增强版，即它们之间的性能差异仅仅被不同的环境构建策略影响。
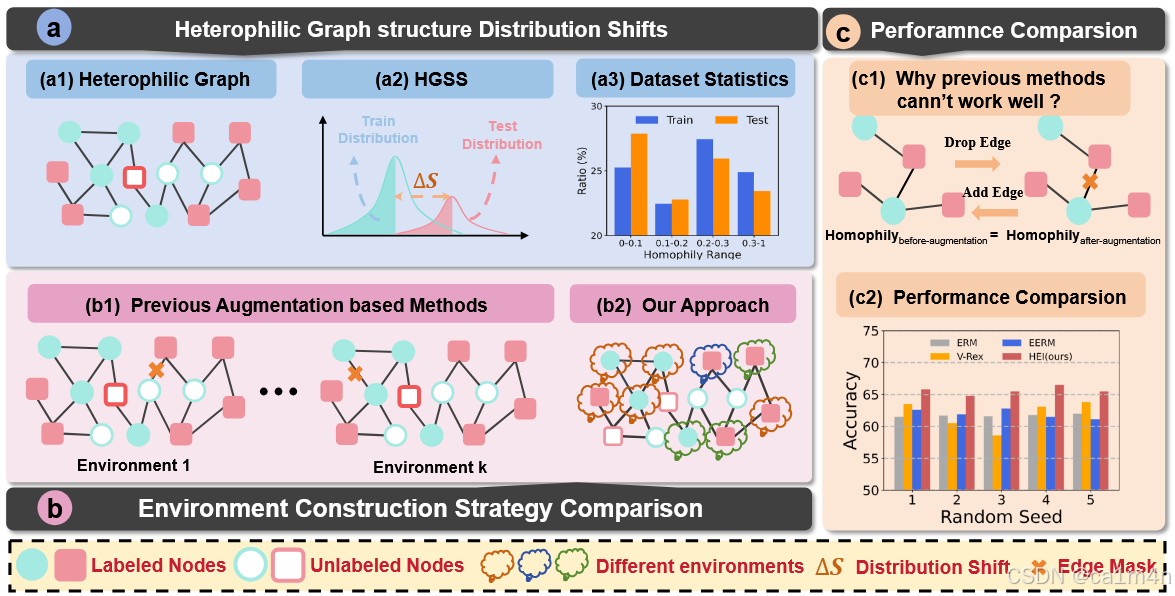图1：（a）展示了异配图结构分布偏移，其中图表和直方图显示了HGSS以及邻接模式在Squirrel数据集上的训练节点与测试节点之间的差异；（b）展示了先前不变学习工作与我们方法在数据增强方面不同环境构建策略的比较；（c）表明先前方法的环境构建可能无法有效解决HGSS，因为邻接模式未发生变化。传统方法与基于图的不变学习方法之间的实验结果可支持我们的分析并验证我们提出的HEI的优越性。

在训练阶段，我们如何确定一个合适的指标来估计节点的邻域模式，并利用它来推断潜在环境以解决HGSS问题。

1.3 Contributions

1. New Issue. 强调了一个重要但常被忽视的异配图结构分布偏移（HGSS），这与大多数专注于backbone设计的异配图神经网络的研究不同；
2. New Framework. 提出了HEI，一种新颖的基于图的不变学习框架，用于解决HGSS问题。与以往不同的是，我们的方法强调利用节点固有的异配信息来推断潜在环境，无需进行增强操作，从而显著提高了HGNN的泛化能力和性能；
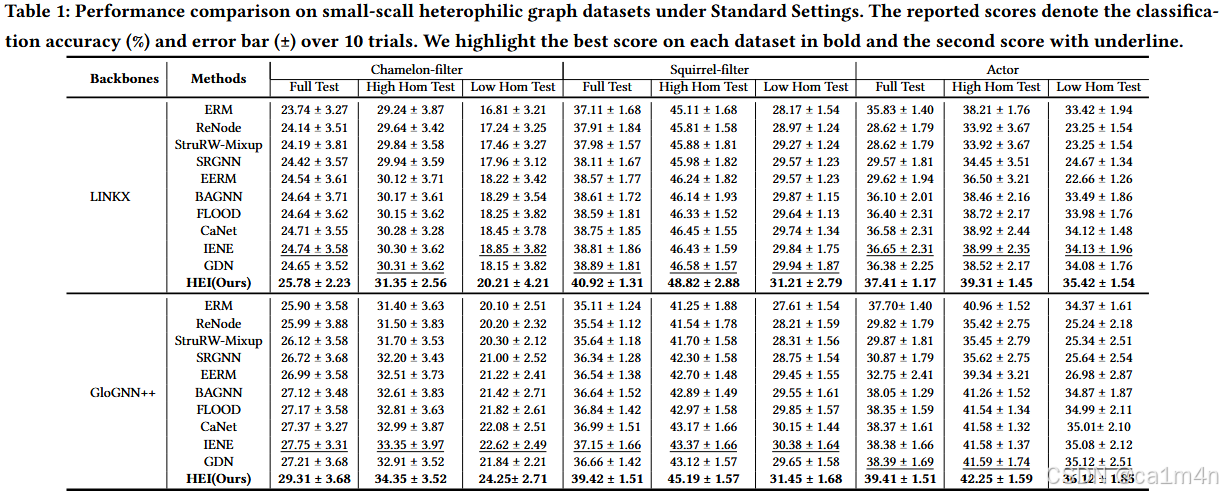
3. Exp. 在多个基准和骨干结构上展示了HEI的有效性。

即，异配图上的OOD泛化，构建环境时利用同配性（结构级别）指标进行构建，先前工作基本是节点级别。

0x02 SmoothGNN：一种用于无监督节点异常检测的平滑感知GNN

Xianyu Dong, et al. SmoothGNN: Smoothing-aware GNN for Unsupervised Node Anomaly Detection. （港中文）

2.1 摘要

在图学习中出现的平滑问题会导致节点表示无法区分，这给与图相关任务带来了巨大挑战。
然而，我们的实验表明，这个问题能够揭示节点异常检测（Node Anomaly Detection, NAD） 中先前研究所忽略的潜在特性。我们引入了个体平滑模式（Individual Smoothing Patterns, ISP）和邻域平滑模式（Neighborhood Smoothing Patterns, NSP），这表明异常节点的表示比正常节点的表示更难进行平滑处理。此外，我们探讨了这些模式的理论意义，展示了ISP和NSP对NAD任务的潜在益处。

受这些发现的启发，我们提出了SmoothGNN，这是一种新颖的无监督节点异常检测框架。
首先，我们设计了一个学习组件来明确捕捉ISP以检测节点异常。
其次，我们设计了一个谱神经网络来隐式学习ISP以增强检测能力。
最后，我们根据我们的发现设计了一个有效的系数，使得NSP可以作为节点表示的系数，有助于识别异常节点。
此外，我们设计了一种新颖的异常度量方法，用于计算节点的损失函数和异常得分，该方法利用ISP和NSP来反映NAD的特性。
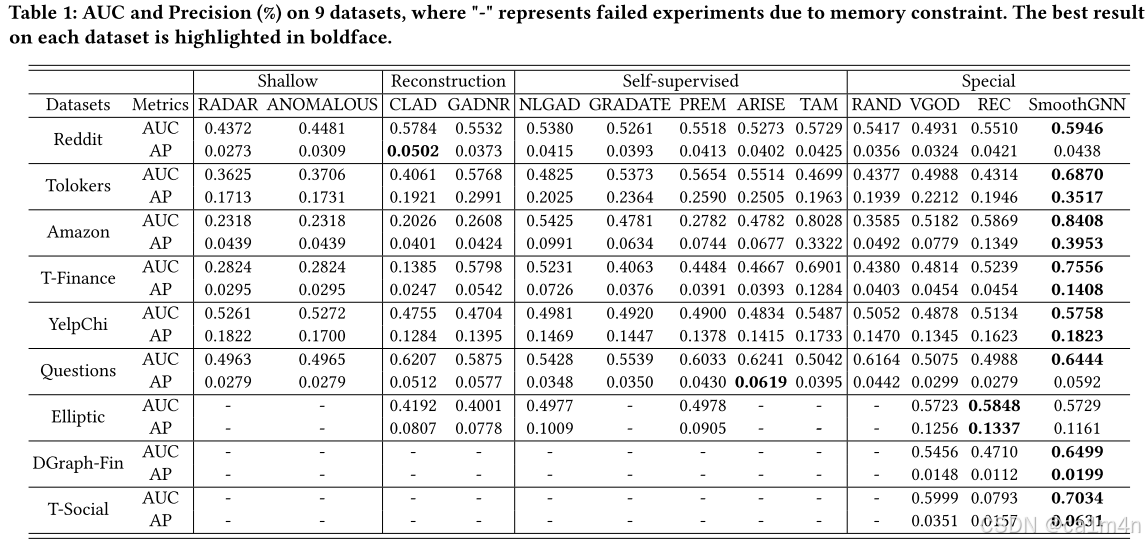
在9个真实数据集上的大量实验表明，SmoothGNN比最佳竞争者平均高出14.66%（AUC）、7.28%（AP），运行速度提升了75倍。

开源代码：SmoothGNN

2.2 背景与动机

节点异常检测的常见应用场景，例如，金融网络中的欺诈检测、社交网络中的恶意评论检测、芯片制造中的热点检测。

在芯片制造中，Hotspot Detection（热点检测）是一项关键的质量控制技术，主要用于识别设计或制造过程中可能导致芯片缺陷的潜在问题区域。这些“热点”通常指设计中容易在光刻、蚀刻或其他工艺步骤中出现故障的局部图案（如短路、断路或可靠性问题），可能影响芯片的性能或良率。
即，工业制造中的缺陷检测

复杂的信息和大规模的现实世界的图对如何有效与高效地检测异常节点提出了挑战，特别是在无监督的设置下。现有方法：浅层模型由于手工规则而表现力有限，重建模型和子监督模型计算复杂度高，特殊模型民林寻找NAD有效标识符的挑战。

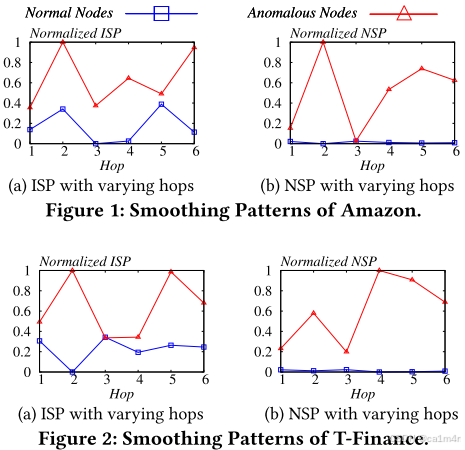
为了解决以上局限性，我们重新评估了NAD任务的传播过程，发现平滑（Smothing）问题可以为检测图中的异常提供潜在优势。具体来说，我们设计了两个新的衡量标准：ISP和NSP，从不同角度分析平滑问题。对于ISP，我们计算在每个传播跳的节点表示和收敛表示后获得的异常和正常节点的无限数量的跳数之间的平均归一化距离。对于NSP，我们分别计算异常和正常节点邻域内的平均归一化相似度。值得注意的是，这两种平滑模式在现实世界的数据集中（如Amazon和T-Finance）的不同类型的节点上表现出不同的行为，分别如图1和图2所示。在传播过程中，异常节点的平滑模式一般超过正常节点在大多数跳数。这一观察结果提供了一个潜在的指标，用于评估节点的异常分数：平滑模式越高，节点越有可能是异常的。

2.3 平滑模式的分析

预备知识

谱GNN图卷积运算可以通过Laplacians的第T阶多项式来近似： $$\mathbf{U}{g}_{\theta }{\mathbf{U}}^T\mathbf{x}\approx \mathbf{U}(\sum _{t=0}^T{\theta }_t{\Lambda }^t){\mathbf{U}}^T\mathbf{x}=(\sum _{t=0}^T{\theta }_t{\mathbf{L}}^t)\mathbf{x}，$$ 其中，$\theta \in {\mathbb{R}}^{T+1}$是多项式系数。

如Figure2所讨论的，每个传播跳处的节点表示与在无限跳数之后获得的收敛表示之间的距离对于异常节点和正常节点表现出不同的模式。
ISP：
$$I(\mathbf{x})=||(P^t-P^{\infty })x|{|}_2^2,$$其中，$P^t$是在传播的第$t$跳之后的传播矩阵，$P^{\infty }$是收敛状态，$x$是图信号。如定义所示，ISP有效地描述了传播过程中每个独立节点的平滑模式，它可以捕获光谱信息和平滑模式。

NSP：$$N(x^t)=\sum _{i,j=1}^n{a}_{i,j}||\frac{x_i^t}{\sqrt{d_i+1}}-\frac{x_j^t}{\sqrt{d_j+1}}|{|}_2^2,$$
其中，$a_{i,j}$表示邻接矩阵$\tilde{A}$的第$(i,j)$项，$d_i$是节点$i$的度，并且$x^t=P^{t}x$。NSP测量相邻节点之间的相似性，指示在传播期间邻域内的平滑模式，NSP与谱空间具有很强的相关性，可以作为节点表示的系数。

我们还可以观察到，在所有层上应用NSP可以在某些数据集上提高性能，但并不是在所有数据集上都是如此。这样的结果证明了NSP的有效性，因为仅将其应用于最后一层或所有层都明显优于基线。因此，为了保持模型的简单性和稳定性，我们只将NSP应用于最后一层。