01数据结构-B树练习及B+树特点

1.B树练习

• 1.在下图所示的5阶B树T中，删除关键字260之后需要进行必要的调整，得到新的B树T1，下列选项中，不可能是T1根节点中关键字序列的是()。
  

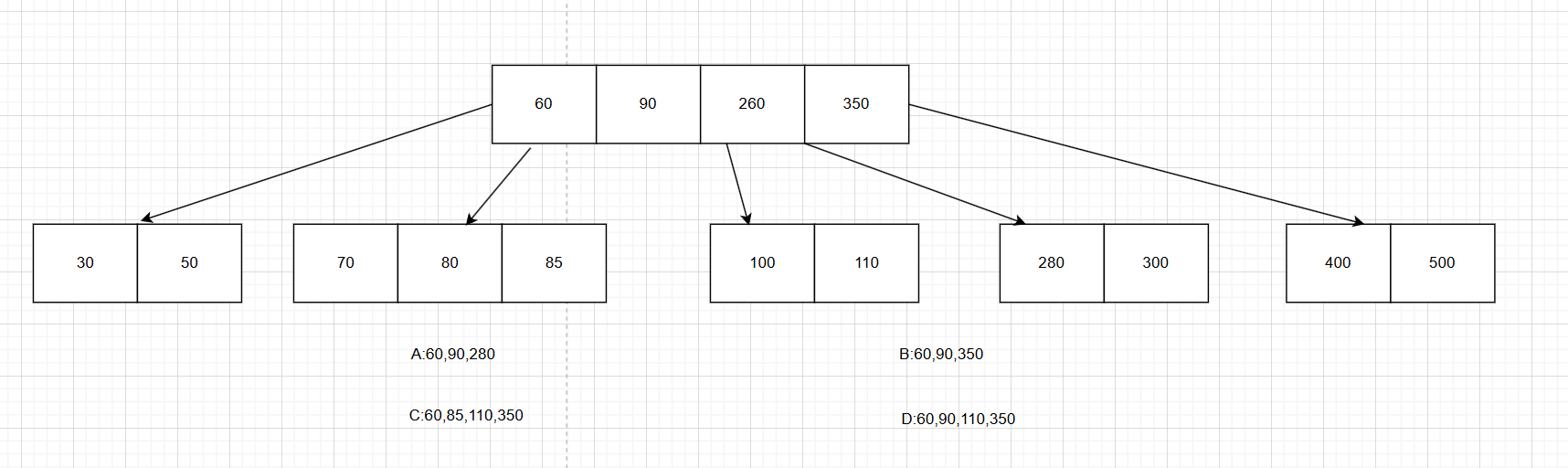
  分析：我们可以发现，260是内部节点，根据上节课我们所讲，删除内部节点的时候我们需要找到他的前驱或后继节点来替换删除：

  • 找前驱节点110，把110的值赋给260，然后直接删除叶子节点中的110，删除后发现不满足节点的下限，根据上节课我们所讲，我们需要向左或右节点借一个来。向左边看，发现左边中的节点有3个数据，可以为我们所用，我们借85，借的规则是将其父节点元素下移至当前节点，将兄弟节点中元素上移至父节点。将90移下来，85移上去，最终效果如图：所以C是对的。

  

  • 找后继节点280，把280的值赋给260， 然后直接删除叶子节点中的110，删除后发现不满足节点的下限，根据上节课我们所讲，我们需要向左或右节点借一个来。此时发现左右均不满足借的条件，只好进行合并：如图，如果按照红色圈内合并（向左合并），那么根节点中的序列就是60，90，360（A），如果按照蓝色圈内合并（向右合并），那么根节点中的序列就是60，90，280（B）。
    

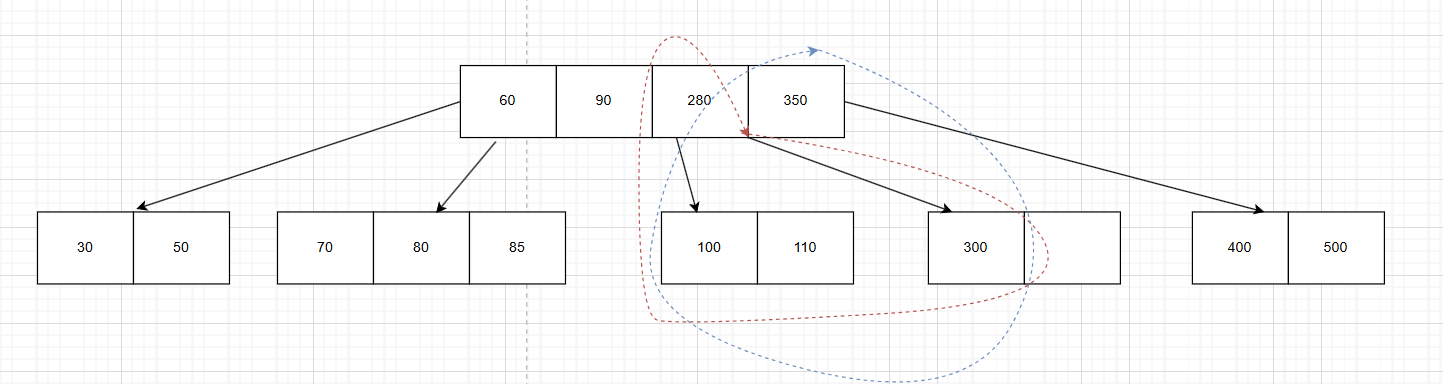
• 2.依次将关键字5，6，9，13，8，2，12，15插入初始为空的4阶B树后，根节点中包含的关键字是（）
  A:8                          B:6,9
  C:8,13                     D:9,12

  分析：4阶B树节点内最多有三个元素，4个叉，注意由于是偶数阶树，在分裂的时候 就会有两种分发，第一种是选择较小的那个数据作为上浮的节点（可以简单理解为左分），第二种是选择较大的那个数据作为上浮的节点（可以简单理解为右分），需要注意的是如果选择了较小的那个数据作为上浮的节点，那后续的所有分裂操作都要按照统一标准，且向左向右分的最终的B树形状可能会不一样，我这里以向左分为例给大家画一下大致草图：
  
  这是前6个数字的插入。注意插入到13的时候需要选择较小的往上分裂
  
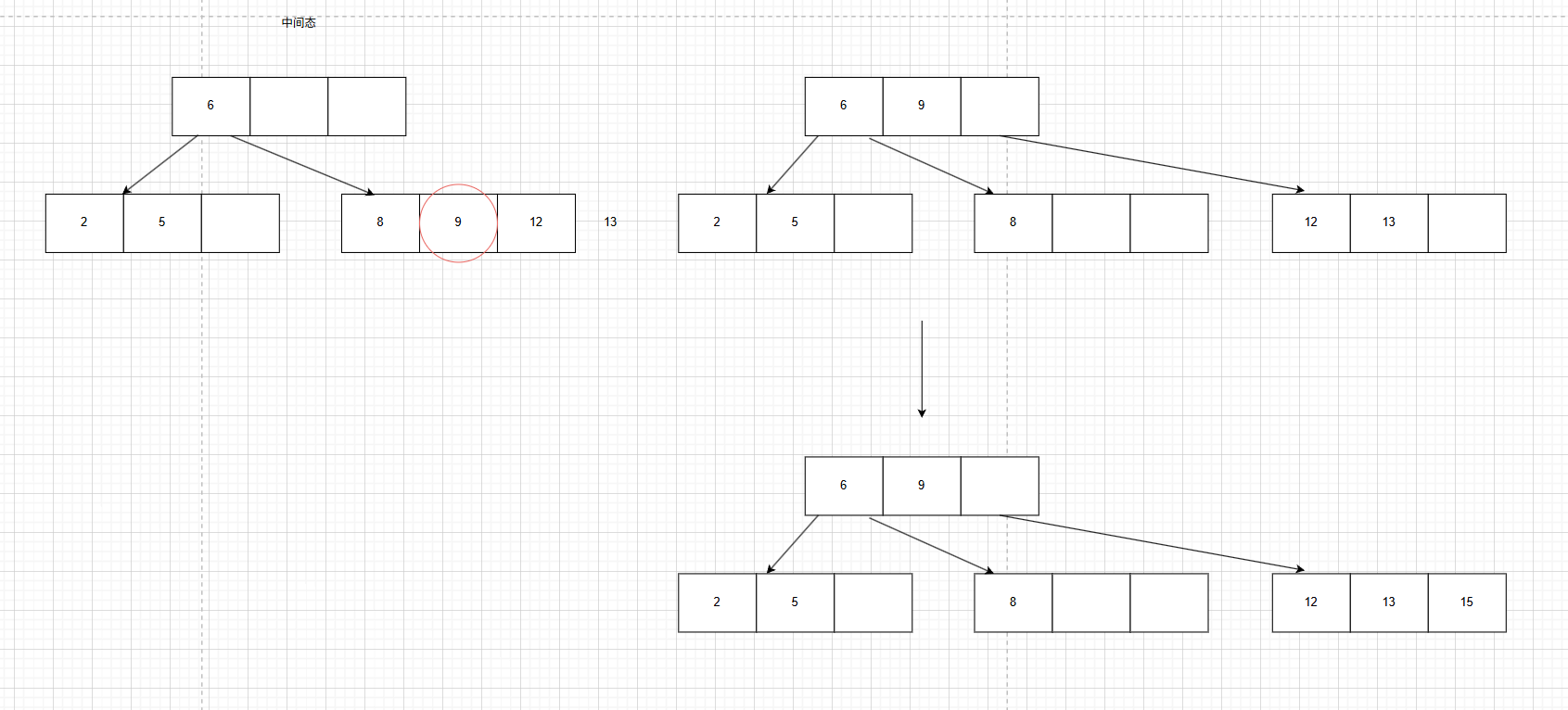
  这是后两个数字的插入，注意插入到12的时候需要选择较小的9往上分裂

2.B+树

2.1为什么需要B+树

在B树中的一个节点中的数据包含数据，key和指针域，通常我们认为这会使得节点内存放的数据量会变少，我们知道一个B树中的一个节点就是一次磁盘IO，假设一个节点能存512个字节数，我们数据一般都会占大头，假设一个数据中的数据，key和指针域占有256个字节，这样一个节点仅可以存放2个数据量，这样树的高度显得没有那么“矮胖”，这有点违背B树设计的初衷。我们希望节点中可以存放更多的数据，让树的高度变得更高，我们想到在数据中就不存放数据，我们只用叶子节点来存放实际数据，内部节点只用来存放key和指针域，这就是我们的B+树，这样在同样的数据量的情况下，B+树的高度会更加的“矮胖”，查找效率会更高。

2.2B+树的性质

B树的节点数据包括了索引和映射，所谓的映射真实使用的数据，B+树的节点只存放索引，叶子节点才放真实映射，内部节点只保留索引值，可以表示更多的索引，真实的数据都存放于叶子节点。叶子节点指向了磁盘中的某个位置。如图：

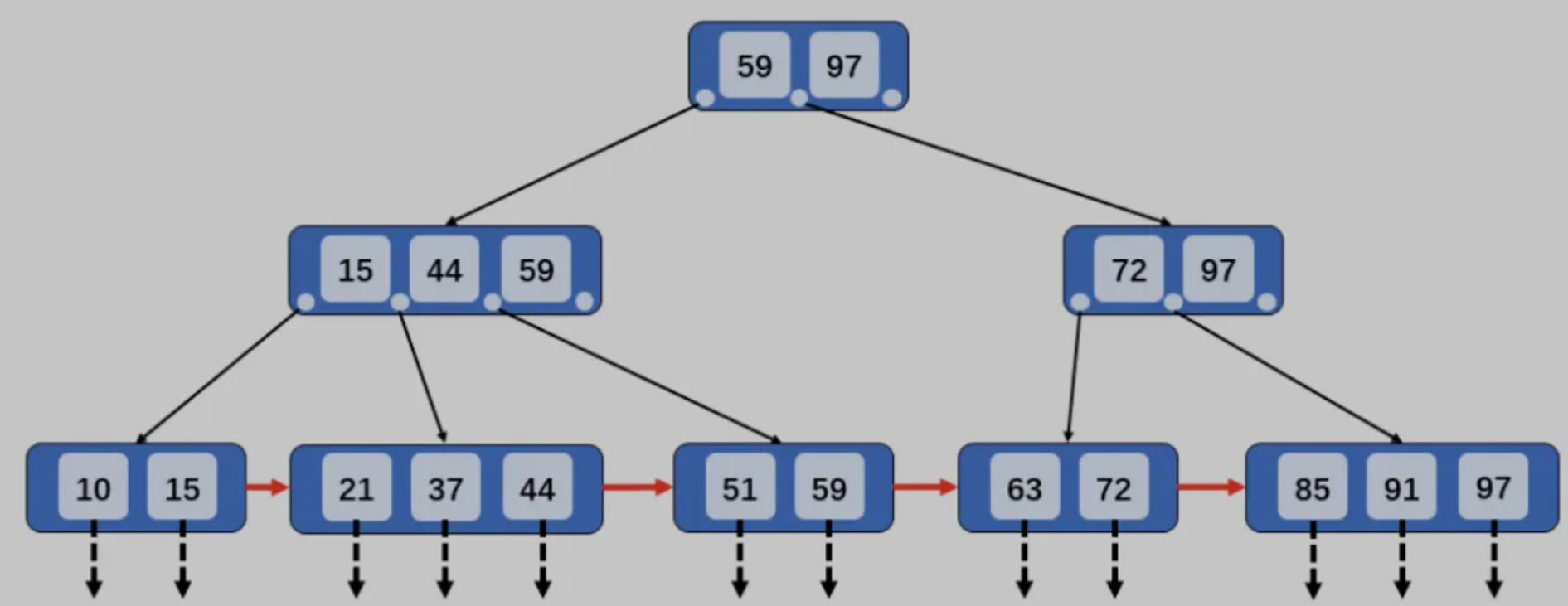
可以看到B+树中似乎出现重复的数据，例如根节点59，97的“左边”节点是15，44，59，中最右边有一个59，通过观察可以发现第二次出现的相同数据都在对应节点的指针域的最右边，实际上这不是“错误”或“冗余”，而是B+树为了保持范围查询的绝对正确性和索引结构的清晰性而故意设计的。这个重复出现的元素充当的是“路标”或“分隔符”的关键角色。由于数据只存在于叶子节点。内部节点中的键纯粹是索引/路标，它们会在叶子节点中作为数据再次出现。这种“冗余”是用少量的空间换取巨大的性能和维护便利性，对于数据库系统来说是绝对值得的交易。

由于我们的节点中会存放一个路标，所以我们B+树中的节点子树个数与关键字个数相等，因为我们会把每个节点中出现的值都放到对应指针指向的节点中作为路标。这一点与B树区别很大。

同时也能看到我们的叶子节点中像链表一样串起来了，注意这些指针域仅存在于叶子节点。这些指针将所有叶子节点按顺序连接成一个有序的双向链表（可以自己定义，不过一般都是双向链表）。这些指针指向的是下一个（或上一个）叶子节点。它们的作用是支持高效的范围查询，一旦找到范围的起点，就可以沿着链表顺序扫描，而无需回溯到树的根部。所以使用B+树在范围内查找的效率是极高的，我们只需找到范围内的第一个元素和最后一个元素，在第一个数据找到叶子节点时，直接通过链表查询到范围内的最后一个元素就可以了，如 WHERE id BETWEEN 12 AND 20。这个功能极度依赖叶子节点的有序链表。反过来我们从这个性质也能看出为什么在上一步我们需要看似“冗余”的数据，为了在叶子节点中也出现之前的元素，方便范围查找。

一颗m阶B+树需满足下列条件：

• 每个分支节点最多有m棵子树（孩子节点）
• 非叶根节点至少有两颗子树，其他每个分支节点至少有ceil(m/2)棵子树
• 节点的子树个数与关键字个数相等
• 所有叶节点包含关键字及指向相应记录的指针，叶节点中将关键字按大小顺序排列，并且相邻叶节点按大小顺序相互链接起来。
• 所有分支节点中仅包含它的各个子节点中关键字的最大值及指向其子节点的指针。

2.3B+树的查找

B+树中的所有数据均保存在叶子结点，且根结点和内部结点均只是充当控制查找记录的媒介，并不代表数据本身，所有的内部结点元素都同时存在于子结点中，是子节点元素中是最大（或最小）元素。每一个叶子结点都有指向下一个叶子结点的P 指针 。

以查询 59 为例进行说明:
第一次磁盘 I/O ：访问根结点 [59、97] ，发现 59 小于等于 [59、97] 中的 59 ，则访问根结点的第一个孩子结点。
第二次磁盘 I/O : 访问结点 [15、44、59] ，发现 59 大于 44 且小于等于 59 ，则访问当前结点的第三个孩子结点 [51、59] 。
第三次磁盘 I/O ：访问叶子结点 [51、59] ，顺序遍历结点内部，找到要查找的元素 59 。

可以看到，由于B+树的内部节点不存放真实数据，所以B+树的查找无论查找成功与否，最终一定都要走到最下面一层节点。

2.4B+树与B树的区别

• m阶B+树，节点中的n个关键字对应n棵子树，而m阶B树，节点中n个关键字对应n+1棵子树
• m阶B树，要保证每个节点不能低于ceil(m/2)个分支数
  • 根节点的关键字数 n ∈ [1, m - 1]
  • 其他节点的关键字数 n ∈ [ceil(m/2) - 1, m - 1]
• m阶B+树，
  • 根节点的关键字数 n ∈ [1, m]
  • 其他节点的关键字数 n ∈ [ceil(m/2), m]
• 在B+树中，叶节点包含全部关键字，非叶节点中出现过的关键字也会出现在叶节点中，而B树中，各节点中包含的关键字是不重复的。
• 在B+树中，叶节点包含信息，所有非叶节点仅起索引作用，非叶节点中的每个索引项只包含有对应子树的最大关键字和指向子树的指针，不包含有该关键字对应记录的存储地址。B树的节点中包含了关键字对应的记录的存储地址。
• B+树的优势就是：
  • 查找时磁盘 I/O 次数更少，因为 B+树的非叶子结点可以存储更多的关键字，数据量相同的情况下，B+树更加 “矮胖” ，效率更高。
  • B+树查询所有关键字的磁盘 I/O 次数都一样，查询效率稳定。
  • B+树进行区间查找时更加简便实用。

B+树的插入和删除逻辑就不写了，感兴趣的可以自行在网上查阅，数据结构大概就写完了，后面几篇博客会写一些竞赛中常用的方法，大概先写这些吧，今天的博客就先写到这，谢谢您的观看。