全文 - Graphene -- An IR for Optimized Tensor Computations on GPUs

Graphene：一种用于在 GPU 上进行优化张量计算的中间表示 (IR)

摘要

        现代 GPU 在硬件层面加速了多维张量 (multi-dimensional tensors) 的计算和数据移动。然而，即使在软件层面为专家而言，表达经过优化的张量计算也极具挑战性。像 CUDA C++ 这样的语言围绕着一维内存中的扁平缓冲区 (flat buffers) 设计，缺乏对多维数据和线程的合理抽象。现有的张量中间表示 (IR) 表现力不足，无法表示 GPU 张量指令所需的复杂的数据到线程的映射 (data-to-thread mappings)。

        本文中，我们介绍了 Graphene，一种用于在 GPU 上进行优化张量计算的中间表示 (IR)。Graphene 是面向张量编译器 (tensor compilers) 和性能专家的低级目标语言，同时，与提供相同级别控制能力的语言（如 CUDA C++ 和 PTX）相比，它更贴近张量计算领域。在 Graphene 中，多维数据和线程被表示为一等张量 (first-class tensors)。Graphene 的张量可以层次化地分解成块 (tiles)，从而允许将优化的张量计算表示为数据块 (data tiles) 和线程块 (thread tiles) 之间的映射。

        我们使用当今深度学习中一些最重要的张量计算来评估 Graphene，包括 GEMM（通用矩阵乘法）、多层感知机 (MLP)、层归一化 (Layernorm)、长短期记忆网络 (LSTM) 和融合多头注意力机制 (FMHA)。我们表明，Graphene 能够表达所有必需的优化，以达到与现有库实现相同的实用峰值性能。用 Graphene 表达的、超越现有库例程的融合内核 (fused kernels)，显著提高了 Transformer 网络的端到端推理性能，并且达到或超过了 cuBLAS(Lt)、cuDNN 以及手工定制内核 (custom handwritten kernels) 的性能。

CCS 概念
软件及其工程 → 并行编程语言；编译器；软件性能。

关键词
中间表示，优化，张量计算，GPU，编译器，深度学习，代码生成

1. 引言

        受加速深度学习计算需求的驱动，现代 GPU 提供了操作多维张量的指令。英伟达的 Volta 架构 [14] 引入了 Tensor Cores，用于在硬件中计算小型矩阵乘法。后来的 Turing [15] 和 Ampere [16] 等架构则导出了通过 GPU 内存层次结构移动多维张量的指令。这一趋势仍在继续，并且这些指令对于在现代 GPU 上实现峰值性能至关重要。

       尽管 GPU 硬件变得更加面向张量，但向程序员和编译器暴露此功能的软件并未发生根本性改变。大多数快速张量指令仅通过英伟达的虚拟指令集架构 (ISA) PTX [19] 暴露，因此需要带有内联汇编的低级 CUDA C++ 代码作为目标。CUDA C++ 没有标准的张量抽象来表示多维数据或线程。这使得表达优化的张量计算变得极具挑战性，即使对专家而言也是如此。

       最先进的张量中间表示 (IR)，如 OpenAI Triton [25] 或 TensorIR [7]，以及深度学习编译器，如 XLA [8] 或 TVM [5]，通常采用以下三种方法之一来表示优化的张量计算：

    (1) 它们依赖供应商提供的库内核 (vendor library kernels)，并将表示优化张量程序的挑战留给库开发人员，而这些开发人员再次使用 CUDA C++ 和 PTX；

    (2) 它们将快速的 PTX 指令作为操作张量的更高级别的内置函数 (built-ins) 暴露（例如，使用 TVM 的 tensorize 原语 [27] 或 MLIR 的 GPU 方言 [13]），但缺乏对一些最重要指令的抽象，因为这些指令需要复杂的数据到线程映射和布局，而这些无法在现有的 IR 中表达；

    (3) 它们向程序员暴露一个高级表层语言 (high-level surface language)，而生成高性能 GPU 代码的重任则由复杂的内置转换通道 (built-in transformation passes) 执行（例如，Triton 的指令选择 [26]），扩展这些通道需要精通成熟编译器的内部知识。

       本文中，我们介绍了 Graphene，一种用于表示在 GPU 上优化的张量计算的 IR。Graphene 具有足够的表达能力，可以显式地表示针对张量指令的高度优化的 GPU 代码，并旨在作为 CUDA C++/PTX 的替代目标语言，且更贴近张量计算领域。我们做出了以下贡献：

        • 我们引入了一种用于表示张量形状、布局和块 (tiles) 的新颖方法。Graphene 的张量可分解为表示为更小的嵌套张量的块。张量元素在内存中的布局不必是连续的，我们能够表示 GPU 张量指令所需的复杂形状和布局。

        • 我们引入了逻辑线程组 (logical thread groups)，用于将 GPU 计算层次结构表示为一个处理单元 (processing elements) 的张量。将线程表示为张量，使我们能够像操作数据张量一样任意地重塑 (reshaping) 和分块 (tiling) 线程，并且它最大限度地减少了所需的内置层次结构。

        • 我们引入了可分解的规范 (decomposable specifications, specs) 作为对集体计算 (collective computations) 和数据移动 (data movements) 的抽象。规范 (Specs) 将数据映射到线程张量，并表示从设备级内核 (device-level kernels) 到线程级可执行指令 (thread-level executable instructions) 的各种计算。我们将 GPU 指令暴露为原子规范 (atomic specifications)，这些规范将其语义描述为对张量的操作。优化的 GPU 内核通过将内核级规范 (kernel-level specs) 层次化地分解为我们知道如何生成代码的原子规范来表达。

        • 在我们的实验评估中，我们表明 Graphene 不仅能够表示最快的单一算子实现 (GEMM)，还能表示深度学习中一些最重要的融合操作 (fused operations)：GEMM + 逐点尾声 (pointwise epilogues)、MLP、LSTM、Layernorm 和 FMHA。我们分别评估了我们的内核，并在使用各种 Transformer 网络的端到端推理基准测试中进行了评估。

2. 优化的 GPU 数据移动

考虑一个优化的 GPU 数据移动的实现。
       英伟达的 Ampere 架构 GPU 能够通过单条指令在内存层次结构 (memory hierarchy) 中移动二维张量。具体来说，ldmatrix 指令 使用一个线程束 (warp，32 个线程) 将最多四个 8 × 8 的矩阵从共享内存 (shared memory) 移动到该线程束各线程的寄存器 (registers) 中。ldmatrix 指令 在快速的库内核中被重度依赖，在 GEMM 内核中，若用等效但更简单的数据移动操作替换它，会导致性能下降高达 17%。

       ldmatrix 指令 规定了一种严格的数据到线程的映射 (data-to-thread mapping)。图 1a 显示了每个线程必须在共享内存中访问的值，图 1b 显示了执行指令后它在寄存器中接收到的值。从概念上讲，一个线程束被划分 (tiled) 成四个各包含八个线程的组。每个八线程组被分配共享内存中一个唯一的 8 × 8 块 (tile)。然后，每个线程访问共享内存中每个 8 × 8 块的一行 (a)，并接收每个 8 × 8 块中两个相邻的值，总共八个值 (b)【注，数据在共享内存中，需要组织成16x16的小矩阵形态。而且这个小矩阵是显存中某大矩阵的子矩阵。更多细节可参考文章：ldmatrix 详解】。

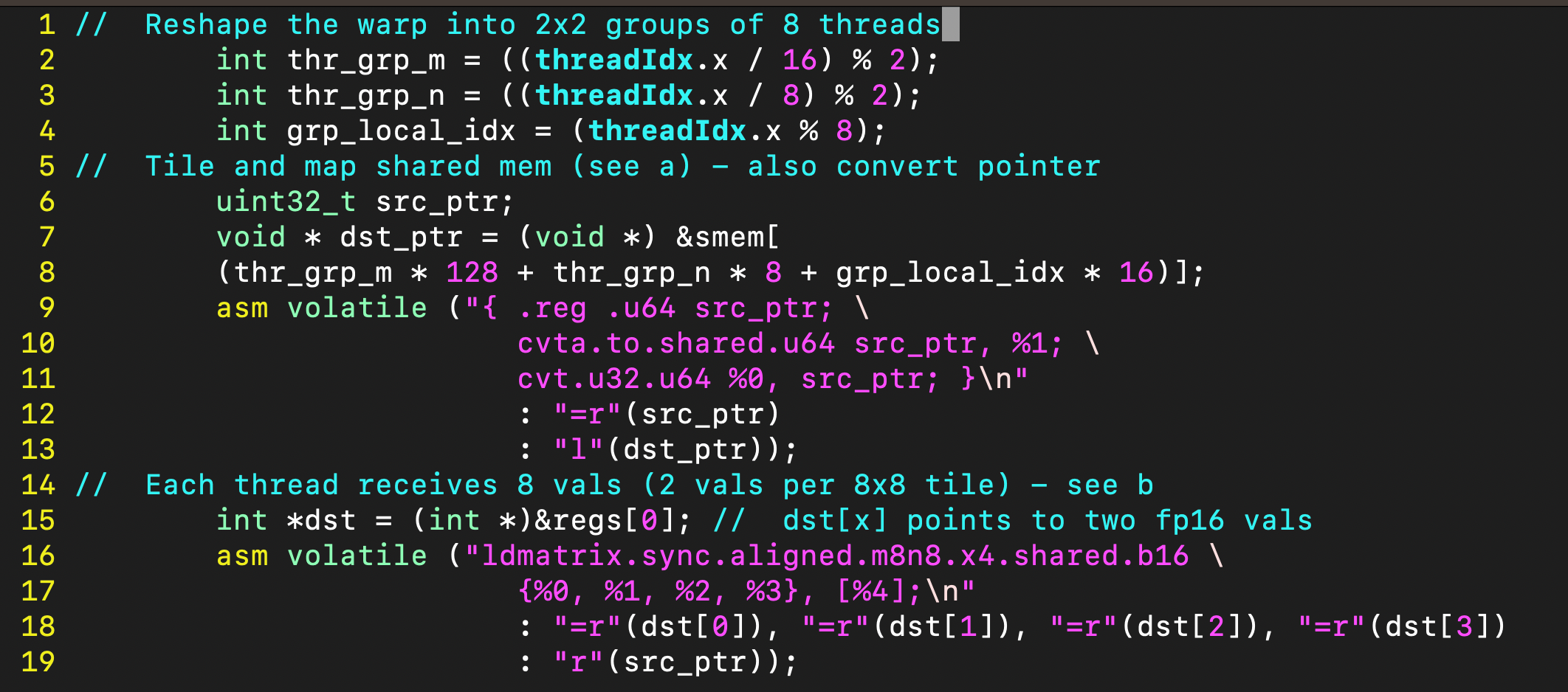
       ldmatrix 指令仅在 PTX 中暴露，需要以图 1c 所示的代码为目标。这就是当前表达优化的 GPU 张量计算的最先进水平，也是性能专家如今必须编写且编译器必须处理的代码类型。该指令的多维特性（在图 1a 和 图 1b 中很容易可视化）在代码中变得极其晦涩难懂：在 CUDA C++ 中，将 warp 概念重塑 (reshape) 为 2×2 的八线程组的操作，必须通过一系列标量线程索引操作（第 1-4 行）来表达。这些操作随后被用作标量索引，来访问共享内存中的一维缓冲区（第 7, 8 行）。由于 CUDA 和 PTX 处理地址空间的方式，我们必须进一步将共享内存缓冲区的访问转换为有效的共享内存指针（第 9-13 行），然后调用 ldmatrix 指令（第 16-19 行）。

「『「『「『 注：

1. 线程组织与内存布局

1.1. 线程分组

int thr_grp_m = ((threadIdx.x / 16) % 2);  // 0或1，表示在M维度上的组
int thr_grp_n = ((threadIdx.x / 8) % 2);   // 0或1，表示在N维度上的组  
int grp_local_idx = (threadIdx.x % 8);     // 组内线程索引(0-7)

这种分组方式将32个线程的warp划分为2x2=4个组，每组8个线程。

1.2. 共享内存地址计算

uint32_t src_ptr;
void * dst_ptr = (void *) &smem[(thr_grp_m * 128 + thr_grp_n * 8 + grp_local_idx * 16)];

这个复杂的地址计算对应特定的内存布局模式：

    thr_grp_m * 128: 在M维度上的偏移（每组128字节）

    thr_grp_n * 8: 在N维度上的偏移（每组8字节）

    grp_local_idx * 16: 组内线程的偏移（每个线程16字节）

2. 内联汇编详解

2.1. 第一部分：共享内存地址转换

asm volatile ("{ .reg .u64 src_ptr; \cvta.to.shared.u64 src_ptr, %1; \cvt.u32.u64 %0, src_ptr; }\n" : "=r"(src_ptr)   : "l"(dst_ptr));

指令解析：

    .reg .u64 src_ptr: 声明一个64位无符号寄存器变量

    cvta.to.shared.u64 src_ptr, %1: 将通用指针转换为共享内存空间的指针

        cvta.to.shared: 转换到共享内存地址空间；

        u64: 64位无符号整数；

        %1: 输入操作数 dst_ptr；

    cvt.u32.u64 %0, src_ptr: 将64位地址转换为32位地址

        %0: 输出操作数src_ptr；

作用： 获取共享内存中目标地址的32位指针，供后续ldmatrix指令使用。

2.2. 第二部分：矩阵数据加载

asm volatile ("ldmatrix.sync.aligned.m8n8.x4.shared.b16 \{%0, %1, %2, %3}, [%4];\n"  : "=r"(dst[0]), "=r"(dst[1]), "=r"(dst[2]), "=r"(dst[3])  : "r"(src_ptr));

指令解析：

    ldmatrix.sync.aligned.m8n8.x4.shared.b16: 矩阵加载指令

        sync: 同步操作，确保warp内所有线程协调执行；

        aligned: 内存地址对齐m8n8: 加载8x8的矩阵块；

        x4: ldmatrix 这次执行会加载 4 个m8n8 矩阵；另解为，x4 表示每个线程加载4个32位寄存器（包含8个fp16值）

        shared: 从共享内存加载；

        b16: 16位数据类型（fp16）；

操作数：

        {%0, %1, %2, %3}: 4个32位输出寄存器，每个包含2个fp16值；

        [%4]: 输入的内存地址src_ptr；

3. 数据流分析

3.1. 加载模式：

        每个线程加载8个fp16值（存储在4个32位寄存器中）

        8个线程协作加载一个8x8的矩阵块

        4个这样的组共同处理16x16的数据块

3.2. 内存访问模式：

    这种布局确保了：

        合并访问   线程以合并的方式访问共享内存

        bank冲突最小化   精心设计的偏移减少了bank冲突

        数据重用   适合矩阵乘法的数据局部性模式

4. 性能优化特点

        Warp级协作   利用warp内线程的协同工作

        共享内存优化   通过地址计算避免bank冲突

        向量化加载   使用ldmatrix指令高效加载矩阵数据

        寄存器重用   一次加载多个值到寄存器供后续计算使用

这种代码结构常见于高度优化的GEMM（通用矩阵乘法）实现，特别是在Tensor Core之前的架构中，通过精细的内存访问模式优化来达到接近峰值性能。

」』」』」』」』

『「『「『「『「『注： Graphen

%1 : [16, 16].fp16.SH    // src
%2 : [ 2, 4].fp16.RF     // dst  //  Tensors (Sec.3)
#3 : [ 1].block
#4 : [32].thread                 //   Logical Thread Groups (Sec.4)
%2 <- Move<<<#3, #4>>>(%1)  {    // Decomposable Specs (Sec.5)// Reshape the warp into 2x2 groups of 8 threads#5 :   [4].[8].thread = #4.tile(8)#6 : [2,2].[8].thread = #5.reshape(0, [2,2])(@thr_grp_m, @thr_grp_n), @grp_local_idx = #6.indices()// Tile and map shared mem (see a) one 1x8 row per thread.%7 : [2, 2].[8, 8].fp16.SH = %1.tile([8, 8])%8 :  [8, 8].fp16.SH = %7[@thr_grp_m, @thr_grp_n]%9 : [8, 1].[1, 8].fp16.SH = %8.tile([1, 8])%10 :  [1, 8].fp16.SH = %9[@grp_local_idx, 0]// Each thread receives 8 vals - 2x2 * 1x2 (see b)
%11 : [2, 2].[1, 2].fp16.RF = %2.tile([1, 2])
%11 <-  Move<<<#3, #4>>>(%10) }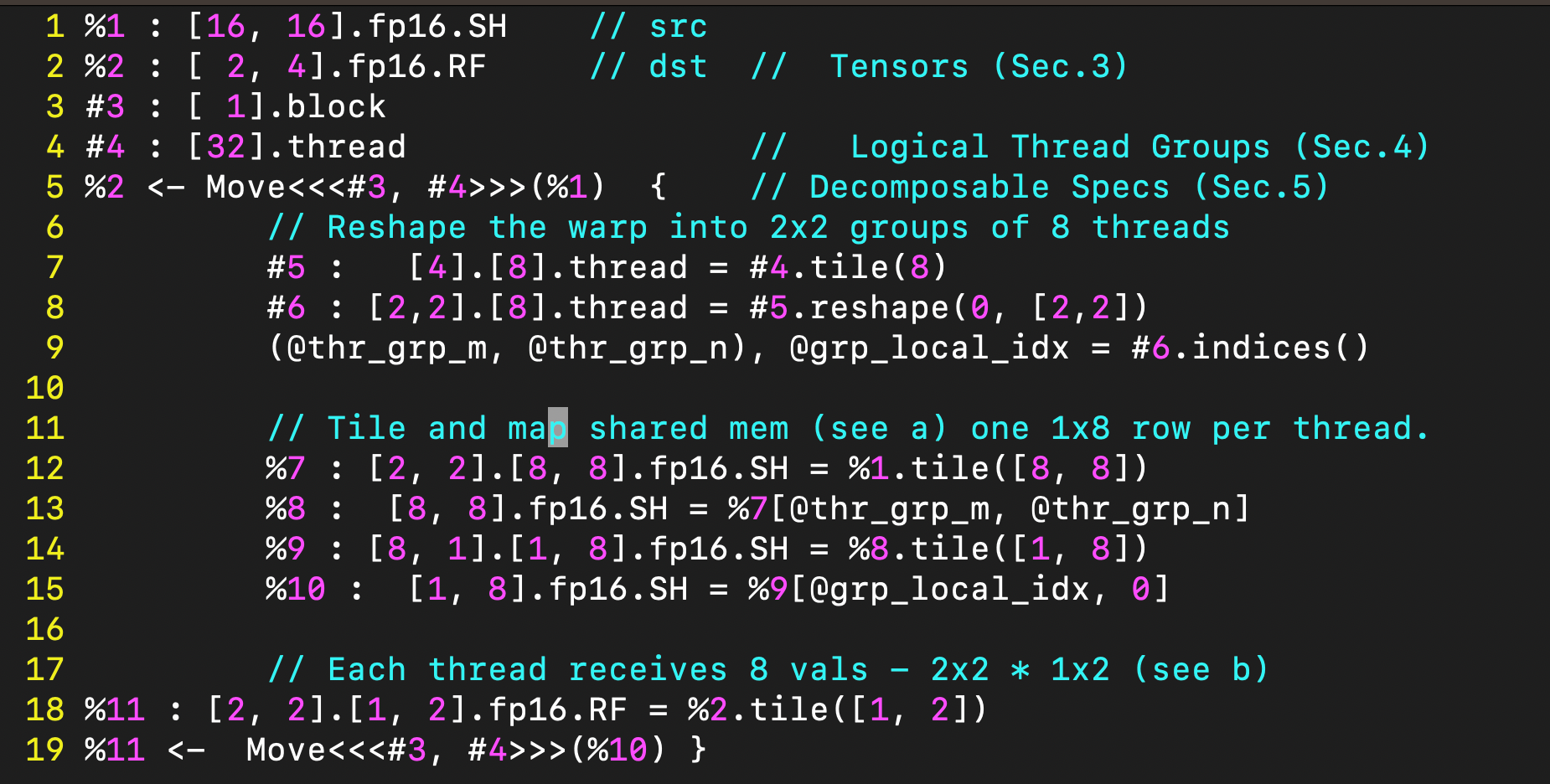

』」』」』」』」』」』

       由于缺乏对多维张量的支持，这种对优化张量数据移动的表达方式编写起来极其困难，且难以理解。据我们所知，现有的张量中间表示 (IR) 无法表示使用 ldmatrix 指令的数据移动，因为它们缺乏表达能力来指定指令所要求的数据到线程的映射。

       图 1d 展示了同一个优化的数据移动在 Graphene 中是如何表示的。所需的数据张量和可用的 GPU 处理单元在前四行中声明。然后，我们描述了一个数据移动操作 (Move)，该操作由每个线程块 (thread-block) (#3) 和每个线程束 (warp) (#4) 执行，将一个 16 × 16 的共享内存张量 (%1) 移动到 2 × 4 的寄存器 (%2) 中（第 5 行）。请注意，寄存器是线程局部的 (thread-local)。2 × 4 个值乘以 32 个线程对应总共 256 个值，足以容纳整个源共享内存缓冲区。

       花括号中的实现（第 7-19 行）显式地应用了 ldmatrix 指令规定的映射（参见图 1a 和 图 1b）。首先，我们将线程束划分成 4 个逻辑线程组 (logical thread groups)，每组 8 个线程，并将这些组重塑为 2 × 2 的形状（第 7-9 行）。接着，源张量被划分成四个 8 × 8 的矩阵（第 12 行），每个线程组一个（第 13 行）。每个 8 × 8 块被进一步划分成行（第 14 行），这些行被分配给各个线程（第 15 行）。最后，目标张量被划分（第 18 行），并且我们指定了另一个在前述定义的块上操作的 Move。这最后的 Move 与预定义的 ldmatrix 指令语义相匹配，在 Graphene 中被视为一个原子规范 (atomic specification)（参见第 5.2 节），无需进一步实现。给定图 1d 所示的 IR，Graphene 会生成上面所示的 CUDA C++ 代码。

3. 未来张量的形态

       在本节中，我们将介绍 Graphene 的张量、它们的形状和布局。在多面体编译 (polyhedral compilation) 领域，多维张量以及将张量分解为块 (tiles) 的研究已有涉及。然而，Graphene 的张量表示特别适合于表达优化的 GPU 计算，主要有两个原因：

1. 我们使用简洁的符号来层次化地将张量分解为块，这些块本身也是更小的嵌套张量。将数据映射到 GPU 的多层计算和内存层次结构需要这种分层块 (Hierarchical tiles)。

2. 我们允许表达非平凡的形状 (non-trivial shapes)，例如包含非连续元素 (non-contiguous elements) 的张量以及具有超越标准“行/列优先 (row/column-major)” 或 “NHWC” 布局的混洗内存布局 (swizzled memory layouts) 的张量。这类布局对性能至关重要，例如，当将中间张量存储到共享内存时。通常使用整数列表来指定张量形状和步长 (strides) 的现有张量 IR 无法表达此类布局。Graphene 的张量表示明确地捕获了当前手工优化实现中使用的所有形状和布局。Graphene 的形状表示法灵感来源于并建立在英伟达的 CuTe 编程模型 [1, 24] 之上，特别是其形状代数 (shape algebra) [17]。

3.1 在 Graphene 中表达张量

       图 2 展示了 Graphene 的张量语法。目前，我们专注于数据张量。由此语法构成的表达式能够将前几节讨论的张量作为一等公民 (first-class citizens) 来表示。在 Graphene 中，每个张量由一个名称、一个形状 (shape)、一个元素类型 (element type) 以及一个指示其存储在 GPU 内存层次结构中何处的标签组成。我们支持标准的 CUDA 内存区域：全局内存 (global memory，片外)、共享内存 (shared memory，片上，由线程块内的线程共享) 和寄存器 (registers，线程局部)。为简洁起见，我们在以下示例中省略内存标签。形状由维度 (dimensions) 和步长 (strides) 组成，两者都用整数元组 (integer tuples) 表示。请注意，我们在图 1 中使用了简化表示法，省略了所有张量的步长。例如，A:[16,16].fp16.SH 实际上被表示为一个行优先张量 A:[(16,16):(16,1)].fp16.SH，其中冒号分隔维度和步长。Graphene 通过两种方式实现高级张量的表达：

       (1) 分层维度 (Hierarchical Dimensions)：IntTuple 是递归定义的。这允许使用多个整数来定义单个维度的大小和步长。这有双重目的：a. 它能够表达复杂的内存布局（第 3.2 节），b. 它能够表达具有非连续元素的张量（第 3.3 节）。
       (2) 块 (Tiles)：张量的 ElementType 是递归定义的，并且可能是另一个嵌套的 Shape。我们使用这一点来表示分层分块的张量 (hierarchically tiled tensors)，其中外部（即左侧）形状表示块的排列，内部形状表示块内元素的排列。

3.2 内存布局

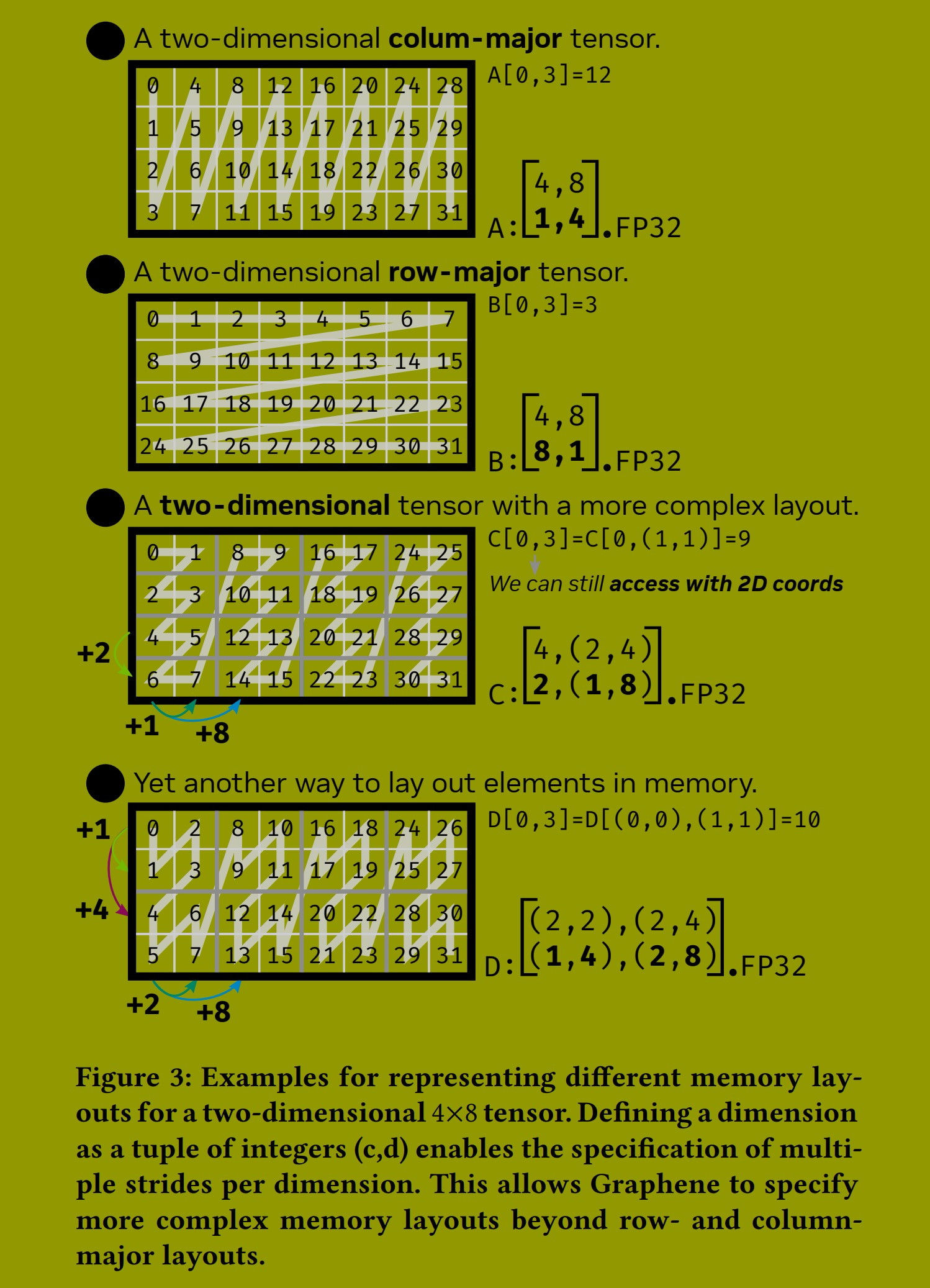
       图 3 展示了在内存中布局一个二维 4 × 8 张量的不同示例。图 3a 和 b 显示了使用相应步长指定的标准列优先和行优先布局。逻辑坐标 (𝑖, 𝑗) 在物理一维内存中的位置是通过计算坐标与张量步长的点积获得的（如张量内的灰色数字所示）。

       像这样用步长表示内存布局是现有张量 IR 中的标准方式。然而，这种表示将可表达的内存布局限制为仅限那些一个维度的所有元素严格出现在另一个维度的元素之前的布局。例如，在如图 3b 所示的 2D 行优先布局中，我们固定一行，在移动到下一行之前遍历所有列。仅仅填充的布局（其中一个维度的步长超过前一个维度的大小，例如 [(4,8):(9,1)]）可以额外用这种格式表达。

       当需要将优化张量计算的中间结果临时存储到共享内存时，这种限制尤其成问题。根据线程读取和写入这些中间张量的方式，需要更复杂的布局来尽可能高效地使用硬件。例如，GPU 上的共享内存被组织成存储体 (banks)，每个存储体一次只能为一个线程服务。一旦多个线程尝试访问存储在同一存储体中的不同值（所谓的存储体冲突，bank conflict），所有冲突线程的访问必须被序列化，这会显著损害性能，因为它会因增加的内存延迟而导致流水线停顿 (pipeline stalls)。实现峰值性能的优化内核通常会以比我们目前描述的简单布局更复杂的方式来布局张量。

       图 3c 和 d 可视化了两种这样的复杂内存布局及其在 Graphene 中的表示。图 3c 显示了一个二维 4×8 张量，其第二个维度表示为一个整数元组而不是单个整数。我们称之为分层维度 (hierarchical dimension)。分层维度使我们能够为每个维度指定多个步长。在这种情况下，我们将两个相邻的列值在内存中连续布局，但在逻辑上先向下移动行，然后再移动接下来的两个相邻列值。图 3d 显示了一个类似但稍复杂的布局，它两次使用了分层维度。

       关键要点是分层维度不会增加张量的秩 (rank)。我们仍然可以使用逻辑二维坐标访问图 3c 和 d 中显示的张量，然后在内部计算相应的分层坐标。这使得可以优化和指定张量的布局一次，例如，在分配时。之后，无论张量在内存中如何布局，人们都可以保持相同的二维逻辑坐标来访问张量。在 CUDA 中表达此类布局也是可能的，但需要复杂的索引运算，而且每次布局更改时，还必须在内核中每次张量访问处进行调整。

3.3 张量分块

       为 GPU 表达优化的张量计算需要指定如何将多维张量映射到多层计算和内存层次结构。Graphene 用于表示这种映射的关键抽象是块 (tiles)。图 4 显示了一个基本的 4 × 8 张量（图 4a）和三个对其进行分块的不同示例 (b, c, d)。

       规则连续块 (Regular contiguous tiles)。块在 Graphene 中表示为嵌套形状。一个分块张量的 ElementType 只是另一个描述块的形状。图 4b 显示了图 4a 的一个分块版本，其中 𝐵 描述了一个包含四个元素（排列为 2×2 的块）的张量，其中每个元素是一个 2 × 4 的浮点元素块。请注意，按照惯例，所有形状的步长都指定了内存中最内层标量类型元素之间的距离，以简化 Graphene 代码生成过程中的索引运算。因此，图 4b 中外部（即左侧）形状的 (2, 16) 步长指定了：要移动到下一个行块，必须跳过两个标量元素；要移动到下一个列块，必须跳过 16 个元素。

       通常，块大小 (tile sizes) 每个维度用一个整数指定，以指明每个块在每个维度包含多少个元素。在 Graphene 中，块大小每个维度用一个一维张量指定。图 4b 中使用的块大小 ([2:1],[4:1]) 解释如下：第一个维度 ([2:1]) 中两个逻辑上相邻的元素和第二个维度 ([4:1]) 中四个逻辑上相邻的元素形成一个块。按照惯例，我们从单位步长张量中省略步长，并且可以如图 1 所示指定块大小。请注意，这种指定块大小的方式与待分块张量的内存布局无关。两个块大小参数都指定了步长为 1，这意味着我们希望将逻辑上相邻的元素分组到同一个块中，而不管它们在物理内存中如何排列。结果张量 𝐵 的步长取决于张量 𝐴 的步长，并自动计算。

Figure 4: Examples for expressing and tiling tensors in Graphene. Tiles are simply nested smaller tensors. Tile sizes are specified with 1D tensors as well. This allows the specification of traditional contiguous tiles (b) as well as noncontiguous tile in one (c) or more dimensions (d). A single dimension can be represented by an integer-tuple (d) which allows to specify more than one stride per dimension.

       非连续块 (Non-contiguous tiles)。一旦我们需要指定在一个或多个维度上不连续的块时，使用张量作为块大小参数就变得特别有用。例如，图 4c 显示了如何将张量 𝐴 分块成形状为 2 × 4 且在第一个维度上交错 (interleaved) 的块。在可视化中，相同颜色的元素仍然属于同一个块。将步长从图 4b 中用于将两个逻辑相邻行分组的 [2:1] 增加到 [2:2]，现在创建的块在逻辑上包含每隔一行。结果张量 C 的步长也反映了这种变化。

       最后，也可以使用具有分层维度的一维张量作为块大小参数，如图 4d 所示。这里，我们表示的块再次包含每隔一行，但现在列维度也是不连续的。具体来说，每个块包含两个逻辑相邻的列 ([2:1])，重复两次，步长为 4 ([2:4])，如颜色所示。请注意，我们已经在高度优化的 GPU 张量计算（如图 1 所示的 ldmatrix 示例）中看到过类似在二维上使用的非连续块。

3.4 参数化形状与部分块

       尽管本文中的所有示例都展示了具体的维度和步长整数值，但 Graphene 能够表示具有参数化（即符号化）形状 (parametric (i.e. symbolic) shapes) 的张量，例如 [M,N].fp32。这对于生成用于具有动态形状的神经网络的内核尤为重要。参数化形状会在代码生成期间导致额外的内核参数。使用参数化形状的索引表达式会使用代数简化规则进行简化，例如 (M % 256) → M 当且仅当 M < 256。

       不能均匀划分输入张量维度的块大小会导致一个或多个所谓的部分块 (partial tiles)（例如，用 128 的块大小对 [1023].fp32 进行分块）。为了表示涉及部分块的实现，Graphene 采用了 CuTe 的过度近似 (overapproximating) 相关形状的方法 [18]。后续对可能包含部分块的张量的访问必须进行谓词判断 (predicated) 以防止越界访问。

4. 逻辑线程组

       高效的张量计算需要在内核的不同位置采用不同的线程排列方式。例如，使用 ldmatrix 进行数据移动期间的线程排列，与使用 Tensor Core mma.m8n8k4 指令 [20] 计算矩阵乘法所需的排列方式显著不同。如第 2 节所述，ldmatrix 指令由线程束 (warp) 内的一组 8 个线程执行。然而，mma.m8n8k4 指令则由每个线程束内一组不同的、八个特定的非连续线程（称为 quad-pairs）执行。如果没有 Graphene，人们必须将所有的线程排列建立为一组标量索引计算，并仔细编排线程如何映射到数据张量（例如，参见图 1c）。

       在 Graphene 中，我们将 GPU 计算层次结构表示为一个张量。这种表示允许像操作数据一样操作线程。对线程张量进行分块 (Tiling) 和重塑 (reshaping) 使得能够将线程排列表达为逻辑线程组 (logical thread groups)。我们方法的优点有两个：

       (1) 显式形状 (Explicit shapes)：逻辑线程组将线程的排列显式地表示为一个多维的分块张量，而不是使用多个标量线程索引计算。高性能内核通常需要在内核内部使用不同的排列，这会导致大量此类索引转换。在 Graphene 中，我们只需拥有不同分块的线程张量，并在代码生成时自动生成所需的标量索引表达式。
       (2) 灵活的层次结构 (Flexible hierarchies)：特定的线程组仅在针对特定架构时才需要。例如，quad-pairs 随 Volta 架构引入，并在更新的架构中再次消失。理想情况是能为所有架构（包括未来的架构）表示高性能代码，而无需为特定的计算层次结构添加内置支持。逻辑线程组使得能够表达任意的线程排列。

       作为张量的线程 (Threads as tensors)。将线程表示为张量的语法与图 2 中用于表示数据张量的语法略有不同。线程张量的 ScalarType 要么是 thread，要么是 block，呼应了 CUDA C++（Graphene 的代码生成目标语言）中的两个基本层次结构。数据张量使用的 Memory 标签对于表示线程张量不是必需的，因此被丢弃。按照惯例，为了在视觉上区分线程张量和数据张量，我们对数据张量名称使用 % 作为前缀，对线程张量名称使用 # 作为前缀。

       示例。图 5 展示了我们如何在 Graphene 中表示第 2 节讨论的 ldmatrix 线程排列。在 CUDA C++ 中表示等效线程排列的相应标量线程索引表达式显示在灰色框中。我们从一个代表一个线程束 (warp) 的、包含 32 个连续线程的一维张量开始（图 5a）。正如前一节讨论的对数据张量分块一样，这个线程束被分块成四个包含八个线程的组，如图 5b 所示。之后，我们通过在分块张量的最外层（深度 0，图 5c）应用 reshape 函数，将这四个块重新排列成一个二维的 2 × 2 形状。在 Graphene 中，允许分块的线程张量具有不同秩 (rank) 的嵌套块。例如这里，这些块是二维排列的，而块内的线程是一维的。相应的索引表达式在 CUDA C++ 代码生成期间自动计算。

       图 6 展示了如何在 Graphene 中表示执行 Volta 的 mma.m8n8k4 指令所需的 quad-pairs。一个 quad-pair 是由八个线程组成的组，由两个特定的 quads（一个由 4 个连续线程组成的组）组成。例如，第一个 quad-pair 由线程 0-3 和线程 16-19 组成。这种排列是由硬件规定的 [20]，必须严格遵守，以避免在使用 Volta 的 Tensor Cores 时出现未定义行为。在 Graphene 中，这种排列通过用一个非连续张量 [(4,2):(1,16)] 对线程束进行分块来表达，该张量精确描述了 quad-pairs 的形状和布局。

5. 规范与分解

       在本节中，我们将讨论 Graphene 如何使用数据和线程张量来表示优化的张量计算。在后续部分中，当我们使用术语“计算”时，我们指的是对张量的操作和数据移动。

5.1 用于表达计算的规范

       对张量的计算由所谓的规范 (Specifications, specs) 表示。这个概念受到 Fireiron [9] 的启发。其核心思想是，规范封装了一个自包含的计算块，例如设备级的矩阵乘法内核或线程束级的数据移动。图 7 展示了在 Graphene 中使用规范的语法。一个规范捕获其输入和输出张量，以及一个描述可用于执行此计算的线程的执行配置 (execution configuration)。可选的分解 (decomposition) 描述了此计算的实现方式，可能包含简单的控制流或其他嵌套的规范。例如，我们通常从一个描述内核级计算的规范开始。然后，我们通过将其逐步分解为更细粒度的规范（通常处理数据和线程张量的块）来描述其实现，直到只剩下我们知道如何生成代码的那些规范。这些剩余的规范称为原子规范 (atomic specifications)，因为它们不需要进一步分解。

       例如，一个 GEMM 内核可以被分解为“更小”的计算构建块，例如，在线程块级别上操作数据块的矩阵乘法，以及这些块在内存层次结构各级之间的数据移动。图 1d 展示了一个具体例子。我们声明了一个从共享内存到寄存器的线程束级数据移动（第 5 行），并逐步将其分解为另一个代表 ldmatrix 指令的嵌套数据移动规范（第 19 行）。

5.2 内置规范

       Graphene 附带一组内置规范 (built-in specifications)。内置规范描述特定类型的计算，而原子规范是内置规范的具体实例，描述由 GPU 指令实现的计算。例如，Graphene 提供了一个内置的 Move 规范来显式表示数据移动，以及一组与不同数据移动指令（如 ldmatrix）相关联的预定义原子 Move 规范。

       表 1 显示了 Graphene 内置规范的完整集合。除了 Move，Graphene 还提供其他内置规范，其原子版本映射到指令集架构 (ISA) 中暴露的不同类型的指令。MatMul 表示类矩阵乘法计算，原子 MatMul 映射到标量和向量化的融合乘加 (fused-multiply-add) 指令以及 Tensor Core 指令。Reduction 和 Unary-/BinaryPointwise 表示预期的计算。Shfl 用于表达数据移动，但不是在内存层次结构各级之间（如 Move 所示），而是在特定的线程组之间。原子 Shfl 映射到线程束级的 shfl.sync PTX 指令。最后，Allocate 用于在另一个规范的实现中引入新的临时数据张量，Init 用于将标量值统一赋给一个张量。

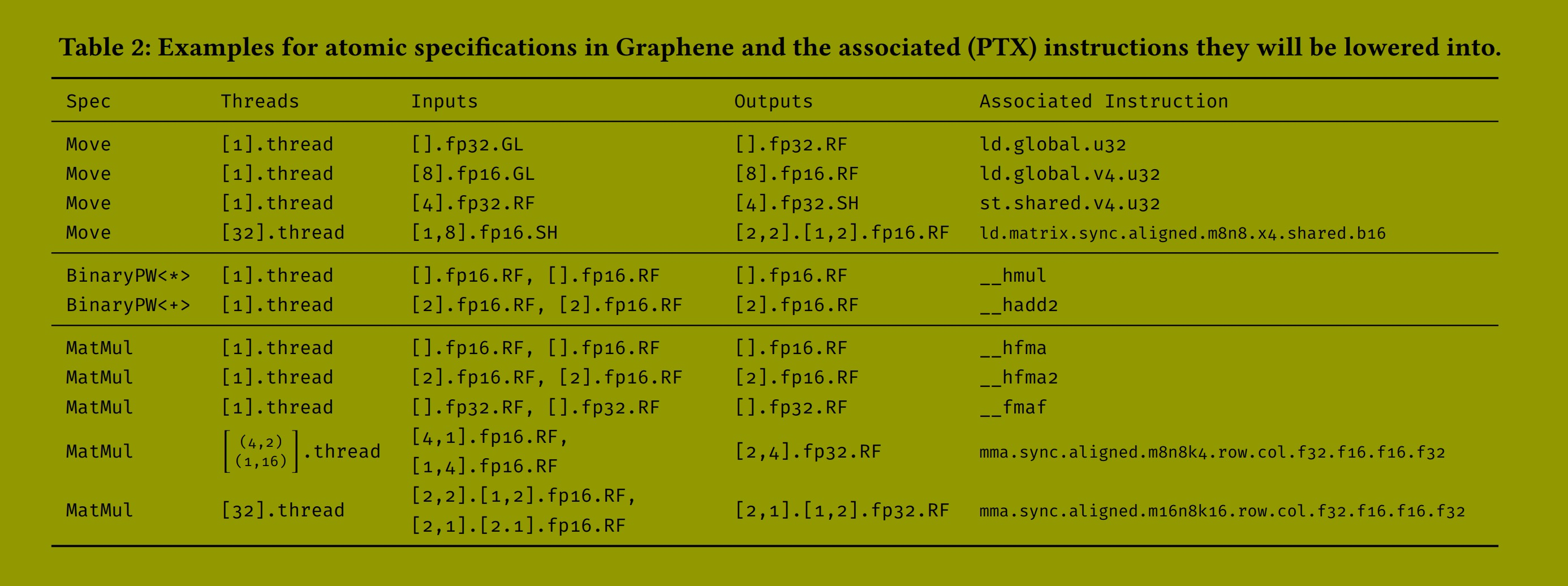
       原子规范 (Atomic Specs)。表 2 展示了 Graphene 中原子规范的示例。在代码生成期间，每个没有分解的规范都会与目标架构的预定义原子规范集进行匹配。例如，每当我们遇到一个 Move（每个线程执行），将一个标量浮点值从全局移动到寄存器（表 2 第 1 行），我们就发出 ld.global.u32 PTX 指令，该指令正好实现此移动。当我们看到一个将八个连续的 fp16 值从全局内存移动到寄存器的 Move 时，我们发出向量化的 ld.global.v4.u32 指令（第二行）。

       像 ldmatrix 这样的张量指令不再按线程执行，而是由线程组协作执行。这些指令也不再操作标量或一维向量，而是操作多维张量。Graphene 的原子规范明确捕获了所需的线程排列和张量形状。例如，表 2 显示了两个代表 Tensor Core mma 指令的原子规范。它们需要不同的线程排列和二维（分块）的输入和输出张量，这些都在我们的 IR 中明确指定。

5.3 表示融合内核

       Graphene 能够表示 GPU 上所有类型的张量计算，包括那些无法由内置规范（如 MatMul）表示的计算。例如，融合内核 (fused kernels) 在一个内核中对张量实现多个操作，例如 GEMM 后接逐点操作 (pointwise operations)。融合内核在现代深度学习网络中被重度依赖以实现最佳性能。为了表示融合计算，我们使用通用规范 (generic Spec)。通用规范描述所需的输入和输出张量以及执行此计算的参与线程。此规范所表示的计算完全由其分解方式定义。

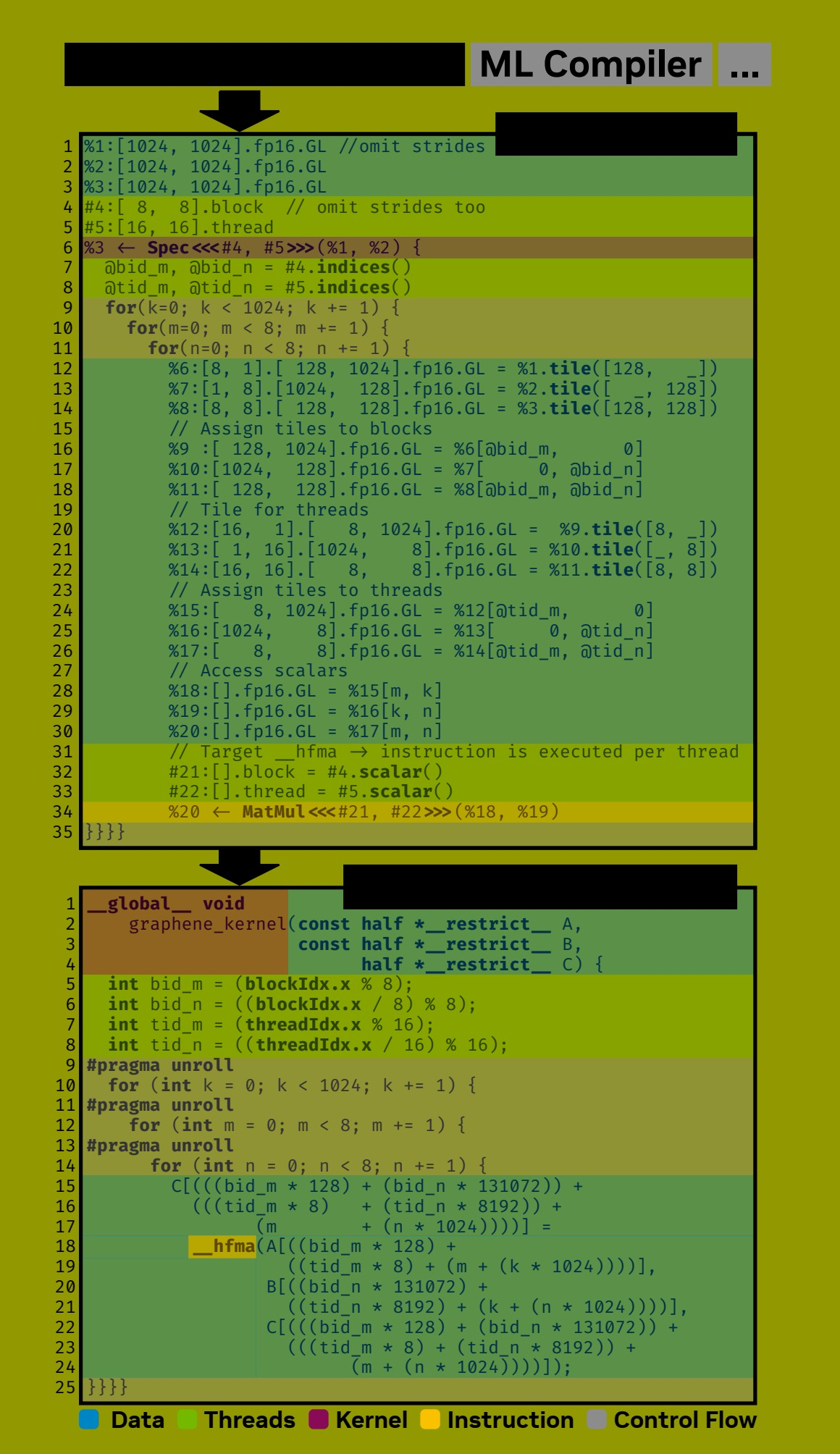
Figure 8: A simple but complete matrix multiplication kernel expressed in Graphene and the resulting CUDA C++ code after code generation. Graphene IR is generated from a simple Python API but could also be integrated into and generated by other machine learning compilers like XLA or TVM.

5.4 示例：一个简单的 GEMM 内核

       图 8 展示了一个实现矩阵乘法的内核级规范的最简单但完整的分解。Graphene IR 并不打算直接编写，因为它冗长且具有冗余的形状注释。目前，我们使用 Python API 生成 Graphene IR。未来，我们设想将 Graphene 集成到现有的深度学习编译器（如 XLA [8] 或 Triton [25]）中，在那里它可以作为 CUDA C++ 和 PTX 的替代目标语言。

       Graphene 代码首先描述了输入和输出张量，以及用于执行此计算的可用线程块和线程（第 1-5 行）。最外层的规范（第 6 行）代表 CUDA C++ 内核。Graphene 还提供基本的控制流语句，包括循环和 if 语句，以及其他不操作张量的表达式，如同步或屏障 (barriers)。在这种情况下，我们使用一个简单的三重嵌套 for 循环（第 9-11 行）来迭代每个线程计算的标量输出元素。我们为线程块分块（第 12-18 行），并立即再次为线程分块（第 20-26 行）。最后，我们指定每个线程的顺序标量计算（第 34 行）。此规范不需要分解，因为它将匹配预定义的原子 hfma 规范（将内部 MatMul 规范的张量类型与表 2 中所示的原子 hfma 规范进行比较）。更优化的 GEMM 实现会描述多次数据移动，并以向量化和 Tensor Core 指令为目标。

5.5 代码生成

       由于 Graphene IR 精确描述了张量计算的实现，生成 CUDA C++ 代码就归结为将 IR 打印为有效的 CUDA C++。Graphene IR 可能包含规范、张量操作或类似循环和条件语句的控制流以及其他不涉及张量的表达式。控制流语句、同步和屏障使用有效的 CUDA C++ 语法发出。没有实现的规范会与原子规范集进行匹配，我们发出对相关指令的调用，如图 8 所示。对于已分解的规范，我们递归地发出它们的实现；对于张量操作，我们构建抽象语法树 (AST) 并将其编译成线程索引和缓冲区访问表达式。生成的索引会进行算术简化。

6. 评估

       在本节中，我们寻求以下两个问题的答案：
Graphene 能否：
(1) 表示在不同架构上与库实现性能相当的核函数？
(2) 在库之外与手工编写的融合核函数竞争？

       用于优化张量计算的中间表示 (IR) 的优劣，取决于其所能表示的核函数的性能。因此，它必须与现有架构上的最先进技术一样好，并且必须能够为所有重要的张量计算生成核函数，包括那些超越单一算子（如 GEMM）的计算。

       方法论 (Methodology)。本节的实验使用了两款 GPU：V100 (SM70, Volta 架构) 和 RTX A6000 (SM86, Ampere 架构)。我们使用 CUDA-11.7、cuBLAS(Lt) 版本 11.10 和驱动程序版本 510.68.02。为了测量性能，我们使用英伟达的 Nsight-Compute 性能分析器 (Version 2021.3.1.0)，它会自动将时钟锁定在基础频率。除非另有说明，所有实验均使用 FP16 张量和 FP32 Tensor Core 累加精度进行。

       本节中的所有图表都在左侧将评估的张量计算显示为数据流图。数据从上向下流动，张量用大写（深绿色）字母表示，标量用小写（浅绿色）希腊字母表示。

假设 A：Graphene 可以表示与高性能库实现相竞争的核函数。
我们达到了与 cuBLAS 和 cuBLASLt 相匹配的性能，这证实了 Graphene 能够表达实现实用峰值性能所需的所有优化。

       GEMM 仍然是当今在 GPU 上执行的最重要且优化程度最高的张量计算。因此，对 GPU 代码效率的最终测试仍然是匹配 cuBLAS 在通用矩阵乘法 (GEMM) 上的性能。英伟达的 cuBLAS 库提供了许多快速的 GEMM 实现，可以被认为提供了实际可达到的峰值性能。那些报告 GEMM 性能超过 cuBLAS 的相关工作，通常只是找到了比 cuBLAS 运行时启发式算法选择的更好的分块大小 [9]。

       在我们的第一个实验中，我们关注 Graphene 是否能够表示达到与 cuBLAS 相同性能的优化 GEMM。具体来说，我们关注的是我们的性能有多接近 GPU 的理论峰值性能。为了最精确地测量 GPU 流式多处理器 (SM) 的平均利用率，我们选择的问题大小要足够大，并能在可用 SM 之间均匀分配工作。我们还确保使用与 cuBLAS 使用的完全相同的分块大小（嵌入在分析器中可见的内核名称中）。

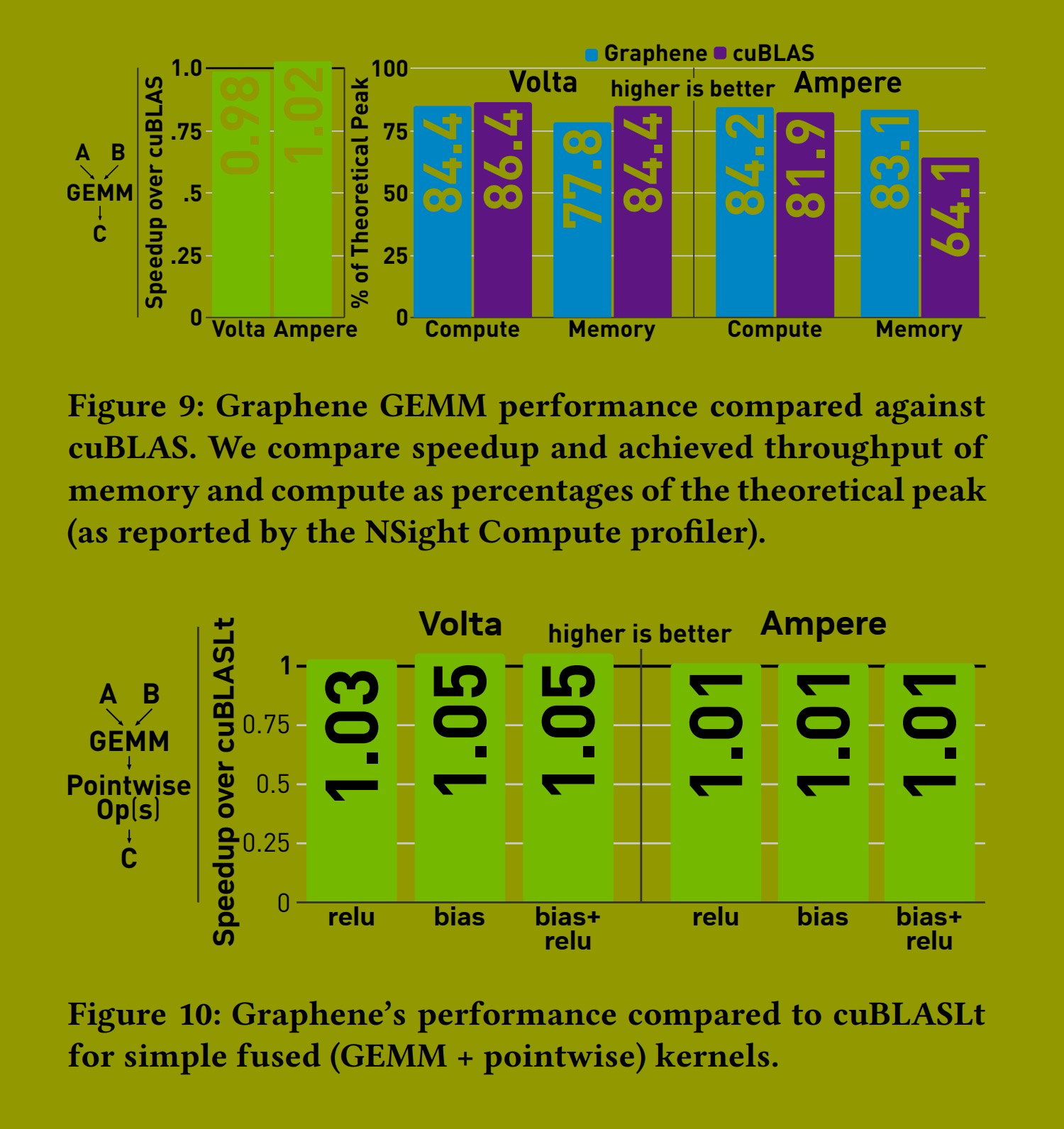
       图 9 显示了 Graphene 的 GEMM 性能与 cuBLAS 在 Volta 和 Ampere 架构上的比较。我们生成的核函数在这两种架构上都与 cuBLAS 的性能完全匹配。因此，Graphene 能够表示等效的优化，以在当今的 GPU 上实现最高的 GEMM 性能。

       本实验中使用的 GEMM 内核是计算受限 (compute-bound) 的，这可以从分析器报告的达到的理论吞吐量（如图 9 右侧所示）看出。这表明 Tensor Cores 以最大容量运行。Ampere 的 cuBLAS 内核比 Graphene 的版本效率稍高，因为它在显著更低的内存吞吐量下实现了相同的性能。然而，由于所有内核都已经是计算受限的，在这种情况下，这些差异不会影响整体性能。

       图 10 显示了 Graphene 与 cuBLASLt 在带有融合逐点操作（例如添加偏置张量或应用修正线性单元 (ReLU) 激活函数）的 GEMM 内核上的性能比较。cuBLASLt 为这些张量计算提供了融合内核。同样，Graphene 生成的核函数在这两种架构上都与高度调优的库实现的性能完全匹配，这证实了我们的第一个假设。

       假设 B：Graphene 为重要的深度学习张量计算生成具有竞争力的融合核函数。
我们发现，对于某些最重要的深度学习张量计算，包括多层感知机 (MLP)、层归一化 (Layernorm) 和融合多头注意力机制 (FMHA)，Graphene 达到或超过了最先进水平，性能提升超过 2 倍。

       在这个实验中，我们分析了 Graphene 生成的融合张量计算核函数（超越单一算子或基本逐点融合）的性能。据我们所知，我们将 Graphene 生成的核函数与针对 GPU 的、针对各个张量计算的已知最快参考实现进行了比较。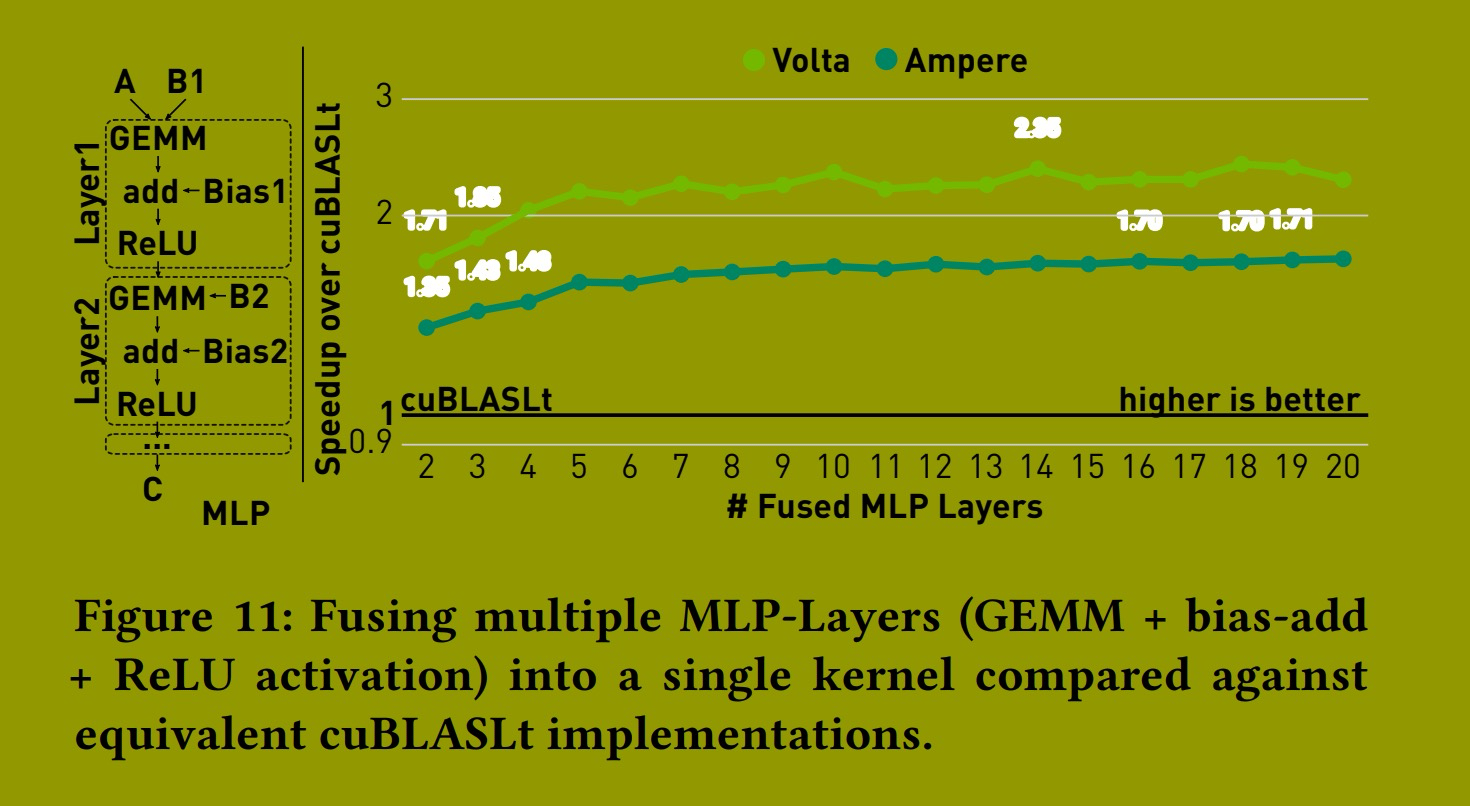

       多层感知机 (MLP)。图 11 显示了 Graphene 在 MLP 上的性能，MLP 是一种经典但仍相关的计算，经常出现在当今的深度学习模型（如 Transformer）中。我们将 Graphene 与 cuBLASLt 进行比较，cuBLASLt 为单层 MLP（GEMM + 偏置加法 + 逐点激活）提供了实现，其单层性能已在图 10 的 "bias+relu" 中显示。对于特定的问题大小，可以将多个 MLP 层融合到单个内核中。在这些情况下，所有中间张量都可以放入 GPU 的共享内存中，从而避免通过较慢的全局内存进行通信。Graphene 的内核实现了这种融合，我们将其与计算多达 20 层 MLP 时 cuBLASLt 调用的累积性能进行比较。

       图 11 显示 Graphene 的性能比 cuBLASLt 高出多达 2.39 倍。这些结果表明：a) Graphene 能够表示超越 GEMM 等单一算子的张量计算，并且 b) 如果问题大小允许，应优先选择融合内核而不是累积的库调用（这通常是深度学习编译器中的默认低级优化方式）。

       长短期记忆网络 (LSTM)。图 12 显示了 Graphene 在简化 LSTM 单元上的性能。我们计算两个独立的 GEMM，然后是一个加法操作和另外两个逐点操作。这种模式是 LSTM 单元中发生计算的基础。通常，LSTM 单元使用 tanh 作为激活函数。然而，为了能够与 CUDA 库实现进行比较，我们必须使用一个略微改动的 LSTM 单元版本，使用 ReLU 而不是 tanh 作为激活函数，因为 cuBLASLt 不提供带有 tanh 的内核。

       使用 CUDA 库实现此计算有两种方法：1) 对图中的每个节点使用一个库内核（总共 5 个内核），使用 cuBLAS 和 cuDNN。这种低级优化策略在许多深度学习编译器中很常见，我们使用此版本作为基线。2) 一个更优化的版本只需要两个库内核：使用 cuBLASLt，第二个 GEMM 可以累加到第一个 GEMM 的输出中（实现后续的加法节点），并额外执行偏置加法和激活操作。

       Graphene 的内核将所有节点融合到一个内核中，因此再次避免了为计算中间结果而与全局内存往返通信。与未融合的基线相比，像这样将计算融合到单个内核中带来了显著的加速（Volta 上 1.75 倍，Ampere 上 1.82 倍）。这种额外的融合超出了当今库的能力范围，这也解释了我们获得的加速。

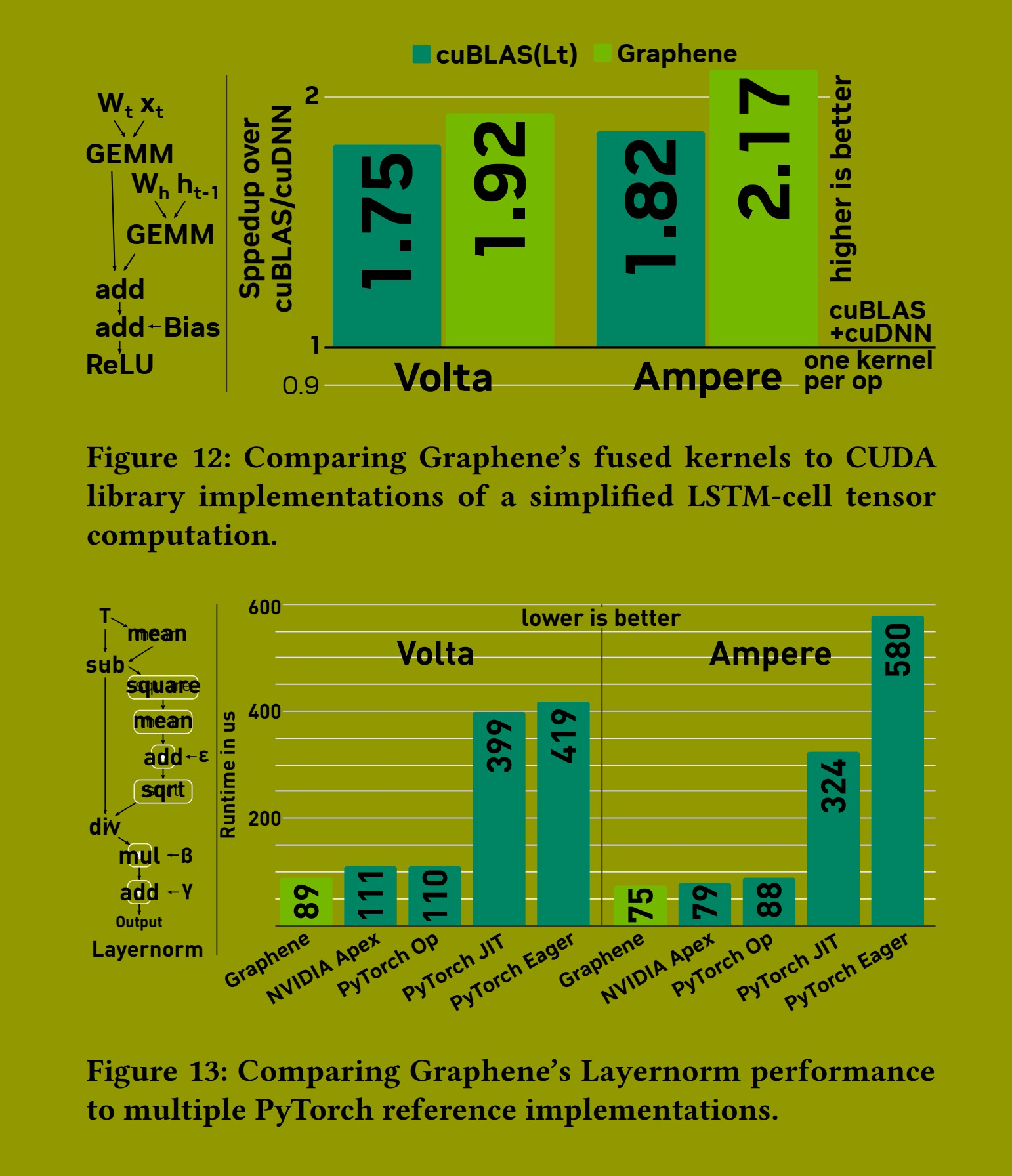
       层归一化 (Layernorm)。图 13 显示了 Graphene 的 Layernorm 性能。Layernorm 特别令人感兴趣，因为它广泛用于 Transformer 等深度学习模型中，并且它不执行任何 GEMM 计算，而是仅包含逐点和归约计算的组合。在这个实验中，我们将 Graphene 生成的核函数与最先进的融合和非融合 PyTorch 实现进行比较。具体来说，PyTorch JIT 和 Eager 显示了使用默认即时执行 (eager execution) 和基于 Torchscript 的 JIT 编译的 PyTorch 性能。我们还测量了两个融合内核的性能：1) 内置的融合 Layernorm 算子，它被低级优化为 PyTorch 附带的预定义 CUDA 内核；2) NVIDIA Apex，它是一个 PyTorch 扩展，为包括 Layernorm 在内的重要计算提供了替代的高性能融合内核。

       再次，我们看到 Graphene 匹配了这种特定张量计算的最知名实现的性能。这表明我们的 IR 能够表示超越 GEMM 的高性能张量计算。

       融合多头注意力机制 (FMHA)。多头注意力 (Multi-Head attention) 是 Transformer 模型的核心计算模式，由两个背靠背的 GEMM 及其间的 softmax 计算组成。softmax 计算本身包含两次归约和几次逐点操作。

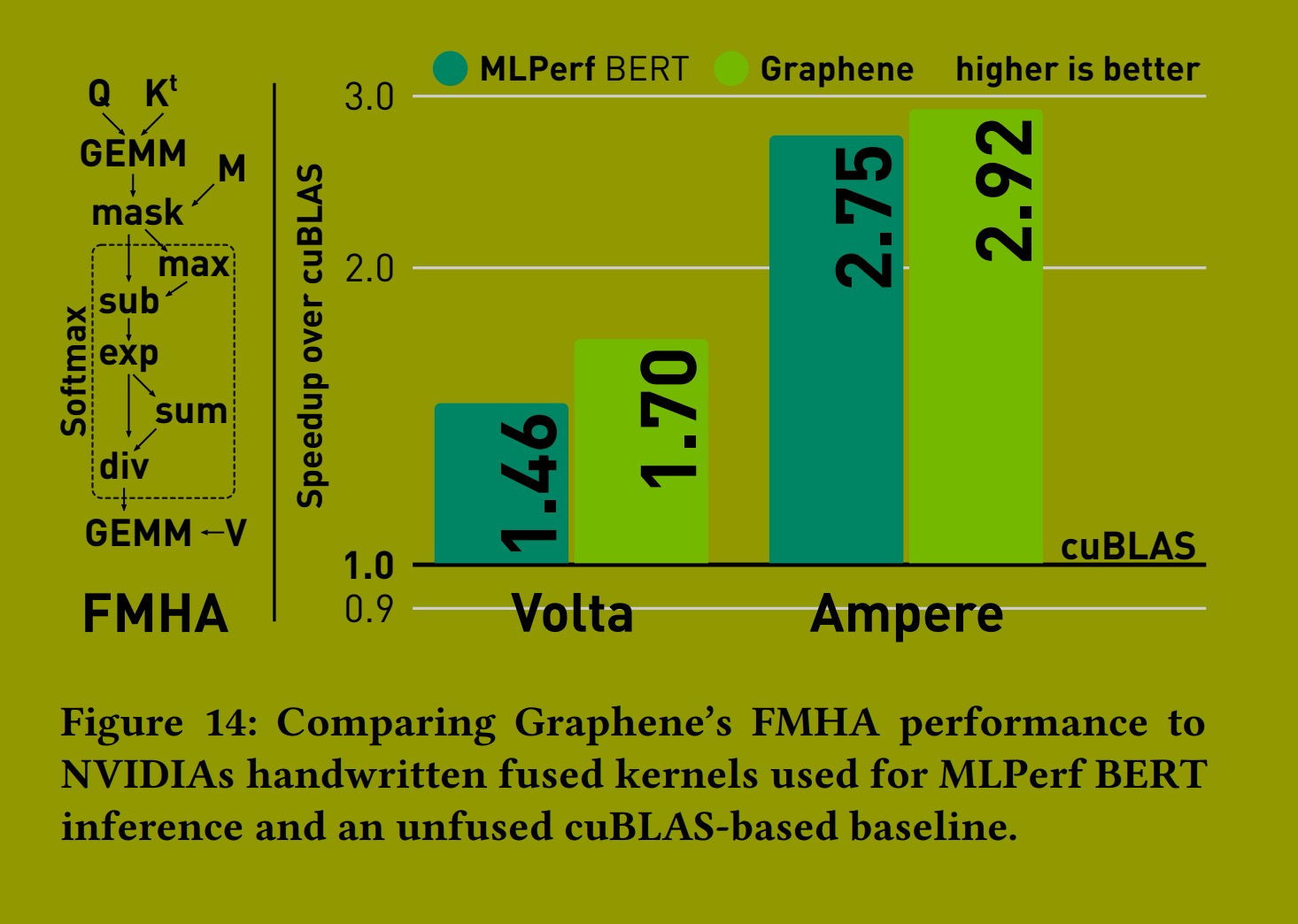
       由于是 Transformer 架构中计算最密集的部分，存在手动融合的内核来加速此计算。图 14 显示了 Graphene 的 FMHA 性能。我们的基线是两次 cuBLAS GEMM 调用和一个采用直接实现的定制 softmax CUDA 内核的累积执行时间。Graphene 的 FMHA 内核专门针对 MLPerf BERT 推理中出现的问题大小（16 个头，批次大小 32，隐藏大小 64，序列长度 384）进行了优化。我们实现了与英伟达融合 FMHA 内核（在 TensorRT 中）类似的融合策略，该策略用于他们提交的 MLPerf BERT 推理 [6]。Graphene 能够为优化的张量计算生成最先进的融合内核，并且由于优化的共享内存布局，我们甚至比 MLPerf 内核实现了小幅加速。

       到目前为止，我们是单独评估我们的张量计算内核。为了评估 Graphene 生成的内核在实践中是否有用，我们还将我们的 FMHA 内核作为自定义算子注入到多个 Huggingface Transformer 网络中。图 15 显示了 Graphene 在 Transformer 家族的五个不同网络上的性能。我们报告了使用自定义 FMHA 内核与常规 PyTorch 推理性能相比所实现的加速，并看到了高达 59% 的改进。

7. 相关工作

        Graphene 深受 Fireiron [9] 的启发。Fireiron 引入了一种专用于 GEMM（矩阵乘法）的调度语言，用于为 GPU 表达优化的矩阵乘法运算。它还引入了用于表示矩阵运算的规范（specifications） 的概念，我们在 Graphene 中扩展了这一概念。Fireiron 的规范仅涵盖矩阵乘法和数据移动，而 Graphene 的规范集能够表示各种类型的 GPU 张量计算，远不止单一的 GEMM 操作。此外，Fireiron 只能处理二维矩阵，而 Graphene 可以处理多维张量。

       作为张量的线程（Threads as tensors）。Graphene 的一个关键新颖之处在于将 GPU 的计算层次结构明确表示为可分解的张量。这受到了分布式深度学习框架的启发，这些框架通常支持指定设备的多维网格。该网格用于将数据维度映射到并行执行单元（在这种情况下是设备，而非线程），这与我们将数据块（data tiles）映射到线程块（thread tiles）的方式类似。此类框架的流行例子包括 Mesh TensorFlow [21]、GShard [12]、GSPMD [31] 和 P2 [30]。与 Graphene 相比，现有的框架都无法支持指定分层的网格/线程。这种层次结构对于表达 GPU 的优化计算至关重要，因为 GPU 的处理单元本质上是分层的（例如，网格（grids）由线程块（blocks）组成，线程块又由线程束（warps）组成，线程束再由线程（threads）组成）。

       用于张量计算的中间表示（IRs for tensor computations）。在表示优化张量计算方面，最密切相关的中间表示（IR）包括 TVM [5] 中使用的 TensorIR [7]、MLIR [11, 28] 和 AMOS [32]。这些 IR 都有一个类似于 Graphene 原子规范（atomic specification） 的概念，用于表示 GPU 上可执行的张量指令。TensorIR 使用预定义的张量内在函数（Tensor Intrinsics），与 Graphene 一样，它描述了张量指令在哪些输入和输出张量上计算什么以及如何计算。MLIR 提供了一个低级的 GPU 方言（dialect），其中包含预定义的操作（ops），这些操作映射到 NVVM 的 WMMA 张量核心指令。AMOS 将可用的 GPU 指令表示为计算和内存抽象（Compute and Memory Abstractions），软件会自动映射到这些抽象上。然而，这些方法都没有明确考虑每条指令执行的线程（例如，Volta 架构的 mma 指令由四元组对（quad-pairs）执行这一事实），而这对于精确表示优化内核至关重要。

       Marvel [4] 和 MAESTRO [10] 能够将分块计算（tiled computations）映射到空间加速器（spatial accelerators），但是，它们未能提供足够的控制力来表达低层级、高度优化的 GPU 内核。

       用于张量计算的代码生成（Code generation for tensor computations）。TVM [5]（使用 tensorize 原语）、Diesel [3] 和 UNIT [29] 是能够自动生成针对 GPU 的高性能张量计算的编译器。UNIT 构建在 TVM 之上，因此两者最终都依赖 LLVM IR 来表示优化的实现。Diesel 是一个多面体编译器（polyhedral compiler），生成带有内联 PTX 汇编的 CUDA C++ 代码。因此，这些编译器都未能克服本文所识别的、在 CUDA C++ 或更低级 IR 中表示优化 GPU 张量代码所面临的挑战。

       Lift [23]、Rise [2] 和 Triton [5] 是用于表示高性能 GPU 代码（包括张量计算）的中间语言。然而，Lift 无法生成使用张量核心（Tensor Core）指令的代码，因此无法在现代 GPU 上提供最佳的张量性能。Rise 最近增加了对张量核心的有限支持 [22]，但仍然缺乏足够的控制力来使用像 ldmatrix 这样的指令进行张量化的数据移动（tensorized data movements）。

       Triton 暴露了一个高级的 Python 领域特定语言（DSL），该语言被转换为自定义 IR，并最终利用张量核心指令降级（lower）为高性能的 LLVM 代码。然而，Triton 的高级 DSL 和 IR 有意抽象了 GPU 张量指令的复杂性，仅在 LLVM 代码生成期间引入它们。这导致了高度复杂的编译器转换通道（transformation passes），扩展这些通道既需要深入了解目标 GPU 架构，也需要了解编译器实现本身。相比之下，Graphene 旨在 IR 层级明确地表达优化计算，并使用直接了当的代码生成方式。

8. 结论

       在本文中，我们介绍了 Graphene，一种用于优化 GPU 张量计算的中间表示（IR）。Graphene 主要解决了表示问题：高度优化的 GPU 内核必须使用 CUDA/PTX 编写，而这对张量计算来说并非合适的 IR。通过引入一个更接近张量计算领域的 IR，我们为机器学习编译器和性能专家提供了一种替代的目标语言。

       Graphene 将数据和线程都表示为一等公民的可分解张量。Graphene 的规范（specs） 是统一的概念，用于表示从内核到可执行指令的各种计算和数据移动。高性能 GPU 代码通过将内核级计算分解为线程级可执行指令来表示。快速张量指令作为原子规范（atomic specs） 暴露，我们在代码生成期间使用内联 PTX 汇编来发出（emit）CUDA C++ 代码。

       Graphene 实现了与手动调优库实现相竞争的（competitive）性能，因此能够代表当今已知的最快内核。此外，Graphene 能够表示尚不存在库例程的融合计算（fused computations），并与手动开发的内核性能相当或更优。我们生成的内核在实际的深度学习网络中部署时实现了显著的加速。因此，Graphene 为新颖的 ML 编译器研究奠定了基础，包括系统性地推导优化张量计算以及生成高性能、架构特定的 GPU 内核。

致谢（ACKNOWLEDGMENTS）

       我们感谢 Young-Jun Ko 分享他的见解并解释如何实现快速融合多头注意力（Fused Multi-Head Attention, FMHA）内核。我们感谢 Andrew Liu 对 Graphene 实现早期原型的反馈。我们感谢 Girish Bharambe 和 Duane Merrill 帮助我们处理各种与低层级性能相关的问题。我们也感谢 Alberto Magni 和 Vijay Thakkar 对论文和图表初稿提出的宝贵反馈。