拆分了解HashMap的数据结构

文章目录

前言

一、底层数据结构总览

二、核心组成部分详解

1. 数组（哈希表）

2. 节点（Node）

3. 红黑树（TreeNode）

三、哈希函数与索引计算

四、哈希冲突的解决

五、扩容机制

六、关键特性与注意事项

总结

---

前言

        在 Java 开发中，HashMap 是高频使用的集合类，从业务缓存到框架底层都离不开它，但多数开发者对其理解仅停留在 “键值对存储”，对 “为何高效”“为何踩坑” 的底层逻辑一知半解。

        面试中 “JDK1.7 与 1.8 的 HashMap 有何不同”“链表为何转红黑树”，开发中 “扩容导致性能波动”“哈希冲突引发查询变慢”，这些问题的答案，都藏在 HashMap 的底层设计里。它不是简单的 “数组 + 链表”，而是融合哈希算法、动态扩容、红黑树的复杂体系，每处细节都是 “时间与空间的权衡”。

        本文将拆解 HashMap 的核心设计：从结构演进（数组 + 链表→数组 + 链表 + 红黑树），到哈希冲突解决、扩容逻辑、红黑树转换，再到 key 的规范细节。无论你是新手还是资深工程师，都能理清设计逻辑，既应对面试考点，也能在开发中合理调优，写出更高效的代码。接下来，我们从 HashMap 的底层结构开始，逐层剖析。

---

HashMap 是 Java 集合框架中常用的实现类（实现 Map 接口），用于存储键值对（key-value）数据，其核心特点是查询、插入、删除效率高（平均时间复杂度为 O (1)），底层通过数组 + 链表 + 红黑树的复合数据结构实现，这种设计是为了平衡哈希冲突带来的性能问题。

一、底层数据结构总览

HashMap 在 JDK 1.8 中进行了重大优化，核心差异如下：

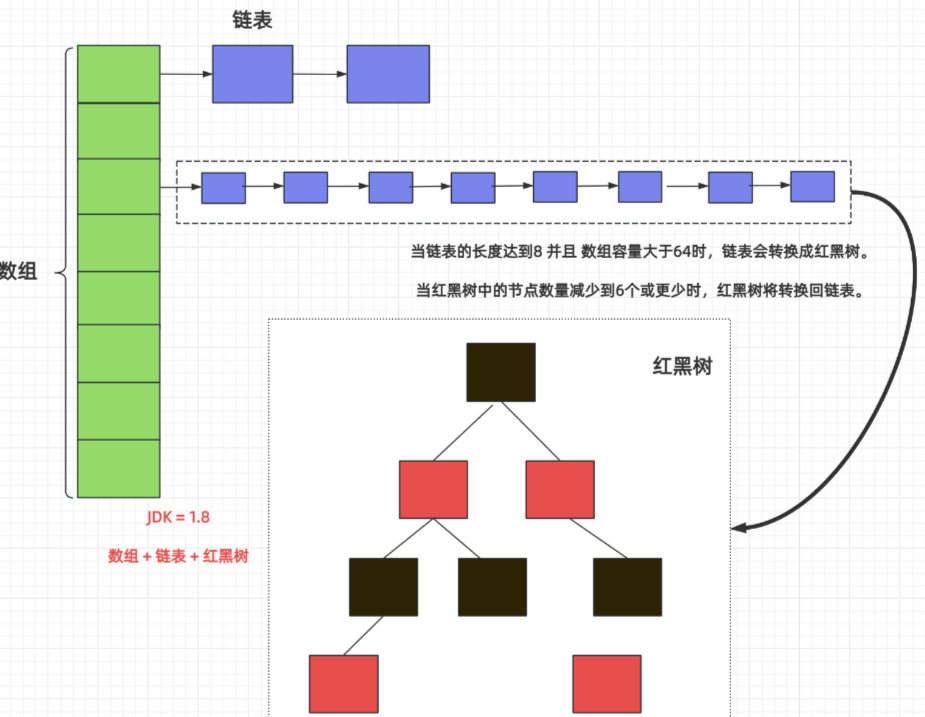
JDK 1.8 及之后，HashMap 的底层结构由三部分组成：

特性	JDK 1.7	JDK 1.8
底层结构	数组 + 链表	数组 + 链表 + 红黑树
链表插入方式	头插法（新节点插入链表头部）	尾插法（新节点插入链表尾部）
扩容时的 rehash	需要重新计算所有节点的索引	利用高位判断，减少计算量
冲突处理效率	链表查询时间复杂度 O (n)	红黑树查询时间复杂度 O (log n)
关键常量	无红黑树相关阈值	引入树化阈值（8）、链化阈值（6）

• 数组（核心容器）：称为「哈希表」或「桶（Bucket）」，是 HashMap 的主体，数组中的每个元素是一个「节点」（Node）。
• 链表：当哈希冲突时，相同索引位置的节点会以链表形式存储。
• 红黑树：当链表长度超过阈值（默认 8）且数组长度 ≥ 64 时，链表会转为红黑树，以优化查询效率（红黑树查询时间复杂度为 O (log n)，优于链表的 O (n)）。

结构示意图如下：

数组索引: 0   1   2        3        ...  n-1|   |   |        |v   v   v        v
节点:   Node Node Node -> Node -> ...  Node|vTreeNode (红黑树节点)

二、核心组成部分详解

1. 数组（哈希表）

• 作用：作为底层容器，直接存储节点（Node），数组的长度称为「容量（Capacity）」。
• 容量特性：默认初始容量为 16，且始终保持为 2 的幂次方（如 16、32、64...）。这是为了通过「与运算」高效计算索引（替代取模运算），同时保证哈希值分布更均匀。
• 索引计算：数组索引由 key 的哈希值通过计算得到，公式简化为：index = (n - 1) & hash（n 为数组长度，hash 为 key 的哈希值经过扰动处理后的值）。

2. 节点（Node）

数组中的元素是 Node 对象，实现 Map.Entry 接口，包含四个核心字段：

static class Node<K,V> implements Map.Entry<K,V> {final int hash;    // key 的哈希值（经过扰动处理）final K key;       // 键（不可变）V value;           // 值（可变）Node<K,V> next;    // 下一个节点的引用（用于链表）
}

• hash：用于定位节点在数组中的索引。
• next：当发生哈希冲突时，通过该字段形成链表（指向同索引下的下一个节点）。

3. 红黑树（TreeNode）

当链表长度超过阈值（默认 8）且数组长度 ≥ 64 时，链表会转为红黑树（TreeNode 继承 Node），以优化查询性能。TreeNode 额外包含红黑树的核心字段：

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {TreeNode<K,V> parent;  // 父节点TreeNode<K,V> left;    // 左子节点TreeNode<K,V> right;   // 右子节点TreeNode<K,V> prev;    // 前一个节点（用于回退为链表）boolean red;           // 节点颜色（红/黑）
}

• 红黑树是一种自平衡二叉搜索树，通过保持「黑色平衡」确保树的高度稳定（约为 log n），避免链表过长导致的查询效率下降。
• 当红黑树节点数减少到 6 时，会重新转为链表（平衡查询和插入效率）。
• 

三、哈希函数与索引计算

HashMap 通过哈希函数将 key 映射到数组索引，核心目的是让 key 均匀分布在数组中，减少哈希冲突。步骤如下：

1. 计算 key 的原始哈希值：调用 key.hashCode()，得到一个 32 位整数（不同 key 可能返回相同值，即「哈希碰撞」）。

2. 扰动处理（哈希值优化）：对原始哈希值进行二次处理，让高位参与运算，减少碰撞概率。
   JDK 1.8 中的实现：

   static final int hash(Object key) {int h;// 若 key 为 null，哈希值为 0；否则，将 hashCode 的高 16 位与低 16 位异或return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
   }
   

    

   作用：将高位信息融入低位，避免因数组长度较小时，高位无法参与索引计算导致的分布不均。

3. 计算数组索引：用处理后的哈希值与「数组长度 - 1」进行「与运算」：

   index = (n - 1) & hash;  // n 为数组容量（2的幂次方）
   

    

   由于 n 是 2 的幂次方，n - 1 的二进制为「全 1」（如 15 是 1111），与运算等价于「取模运算」，但效率更高。

四、哈希冲突的解决

哈希冲突指不同 key 经过计算得到相同的数组索引。HashMap 采用链地址法（拉链法） 解决：

• 当冲突发生时，新节点会被添加到该索引位置的链表尾部（JDK 1.8 后）。
• 若链表长度超过阈值（默认 8）且数组长度 ≥ 64，链表转为红黑树；若数组长度 < 64，则先触发扩容（而非转树），避免数组较小时频繁树化。

五、扩容机制

当 HashMap 中的元素数量（size）超过「阈值（threshold）」时，会触发扩容（resize），以减少哈希冲突。

1. 阈值计算：threshold = 容量（n） × 负载因子（loadFactor）。

   • 负载因子默认 0.75（JDK 设计的平衡值：既避免空间浪费，又减少冲突）。
   • 例：初始容量 16，阈值 = 16 × 0.75 = 12，当元素数 > 12 时触发扩容。

2. 扩容过程：

   • 新容量 = 原容量 × 2（始终保持 2 的幂次方）。
   • 重新计算阈值（新容量 × 负载因子）。
   • 重建哈希表：将原数组中的所有节点重新计算索引，迁移到新数组中（此过程称为 rehash）。
   • JDK 1.8 优化：rehash 时，节点新索引要么是原索引，要么是原索引 + 原容量（无需重新计算哈希值，仅通过判断高位即可），减少计算开销。

六、关键特性与注意事项

1. 无序性：节点存储位置由哈希值决定，遍历顺序与插入顺序无关（如需有序，可使用 LinkedHashMap）。
2. 线程不安全：多线程环境下可能出现死循环（扩容时）或数据不一致，需使用 ConcurrentHashMap 替代。
3. key 特性：
   • 允许 key 为 null（仅允许一个，索引固定为 0）。
   • key 需重写 hashCode() 和 equals() 方法（否则可能导致无法正确查询、删除元素）。
4. 性能影响因素：容量、负载因子、哈希函数的优劣直接影响冲突率，进而影响性能。

七、key 的 hashCode () 和 equals () 规范

HashMap 对 key 的两个方法有严格要求，否则会导致数据异常（如无法查询到已插入的元素）：

1. equals () 相等的对象，hashCode () 必须相等
   若 a.equals(b) == true，则 a.hashCode() == b.hashCode() 必须成立。否则会导致两个相等的 key 被映射到不同索引，无法正确查询。

2. hashCode () 相等的对象，equals () 可以不相等
   这会导致哈希冲突，此时通过 equals () 区分节点（遍历链表 / 红黑树时，需用 equals () 比较 key 是否真正相等）。

3. 最佳实践
   重写 hashCode () 时，应结合对象的关键属性，且保证：

   • 属性不变时，hashCode () 返回值不变。
   • 尽量让不同对象的 hashCode () 分布均匀（减少冲突）。

总结

        HashMap 是「数组 + 链表 + 红黑树」的复合结构，通过哈希函数定位元素，链地址法解决冲突，扩容机制平衡空间与性能，最终实现高效的 key-value 存储与访问。其设计体现了时间复杂度与空间复杂度的权衡，是 Java 中最常用的集合类之一。