7 排序算法通关指南：从 O (n²)（选择 / 冒泡）到 O (nlogn)（快排 / 归并）+ 计数排序

3 选择排序

选择排序的基本思想： 每⼀次从待排序的数据元素中选出最⼩（或最⼤）的⼀个元素，存放在序列的起始位置，直到全部待 排序的数据元素排完。

. 在元素集合 array[i]--array[n-1] 中选择关键码最⼤(⼩)的数据元素

1. 若它不是这组元素中的最后⼀个(第⼀个)元素，则将它与这组元素中的最后⼀个（第⼀个）元素 交换

2. 在剩余的 array[i]--array[n-2]（array[i+1]--array[n-1]） 集合中，重复上述步 骤，直到集合剩余 1 个元素

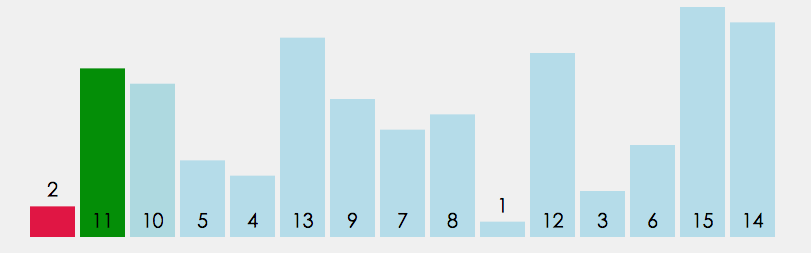
//每次在待排数组中选出最大或者最小的
void selectsort(int* arr,int n)
{for (int i = 0; i < n-1; i++){int min = arr[i];//假设数组当前元素是最小的，int index = i;//假设当前待排元素中最小的下标是自己,不然如果当前元素就是最小的也不会有问题就是自己和自己交互//而已for (int j = i + 1; j < n; j++){if (arr[j] < min) //如果有元素比当前元素小{index = j;//记录当前元素下标min = arr[j];//更新当前最小值}}Mysawp(&arr[i],&arr[index]);}}

直接选择排序的特性总结：

1. 直接选择排序思考⾮常好理解，但是效率不是很好。实际中很少使⽤

2. 时间复杂度： O(N 的平方)

3. 空间复杂度：O(1)

4 交换排序

1 冒泡排序

前⾯在算法题中我们已经接触过冒泡排序的思路了，冒泡排序是⼀种最基础的交换排序。之所以叫做 冒泡排序，因为每⼀个元素都可以像⼩⽓泡⼀样，根据⾃⾝⼤⼩⼀点⼀点向数组的⼀侧移动。

//冒泡排序
void bubblesort(int* arr, int n)
{for (int i = 0; i < n - 1; i++)//趟数==数组大小-1，3个数排两趟{int flag = 0;for (int j = 0; j < n-i-1; j++)//每一趟交换{if (arr[j] > arr[j + 1])//如果前面的元素比后面的元素大就交换{Mysawp(&arr[j], &arr[j + 1]);flag = 1;}}//如果标志位没有改变说明数组已经有序了；if (flag == 0)break;}
}

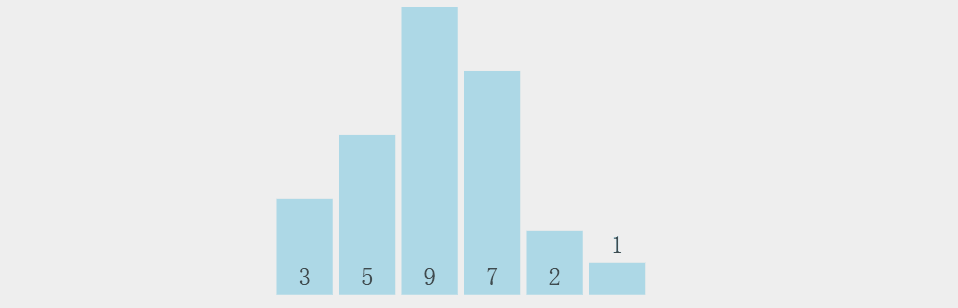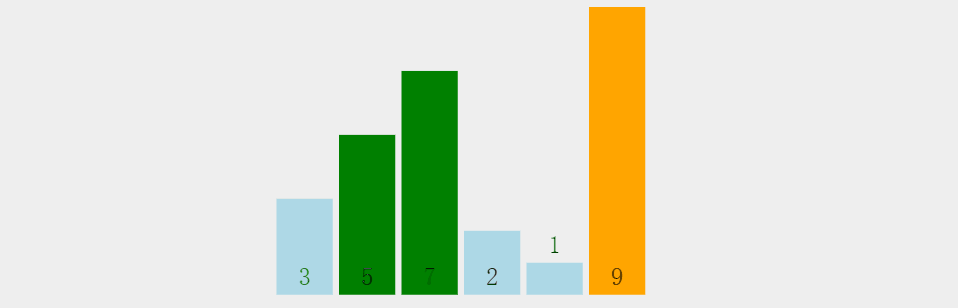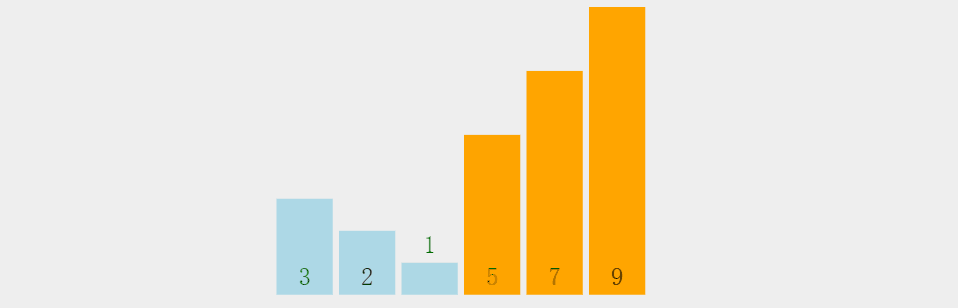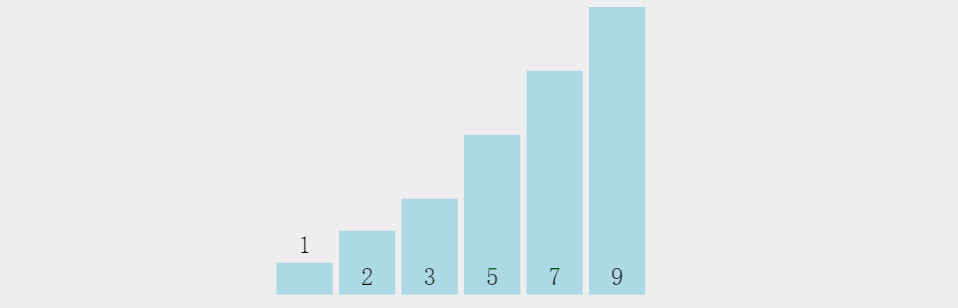
2 快速排序

前置知识--颜色划分

https://leetcode.cn/problems/sort-colors/submissions/634958915/

//划分思想:把数组划分成三个部分，一个是小于key的部分，一个是等于key和待比较的部分，一个是大与key的部分，0-left区间是小于key的值，left+1到i-1是等于key的，i到right-1是待检查的，right后面的区间就是大于key的。
//left指向小于key区间的最后一个元素的位置，
//right指向大于key区间的最后一个元素位置，
//i指向待检查元素位置。
class Solution {
public:void sortColors(vector<int>& nums) {int left=-1,right=nums.size(),key=1;int i=0;while(i<right){if(nums[i]>key)//如果当前元素是大于key的{--right;//把该元素加入到right区间，i不要动因为right-1的元素是没有检查的swap(nums[i],nums[right]);}else if(nums[i]<key)//当前元素小于key{++left;//加入到0-left区间，i++,因为交换过来的元素是等于key的swap(nums[i],nums[left]);i++;}else{i++;}}}
};

快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法，其基本思想为：任取待排序元素 序列中的某元素作为基准值，按照该排序码将待排序集合分割成两⼦序列，左⼦序列中所有元素均⼩ 于基准值，右⼦序列中所有元素均⼤于基准值，然后最左右⼦序列重复该过程，直到所有元素都排列 在相应位置上为⽌。

将区间中的元素进⾏划分的 _QuickSort ⽅法咱们用上面提到的方法即可，还有别的方法可以去网上查一下

void Mysawp(int* a1, int* a2)
{int temp = *a1;*a1 = *a2;*a2 = temp;
}
//快排升序
void Qsort(int* arr,int left,int right)
{if (left >= right)return;int _letf = left - 1, _right = right + 1,i=left;int key_index = rand() % (right - left + 1) + left;//随机选择基准元素int key = arr[key_index];while (i < _right){if (arr[i] > key)Mysawp(&arr[i],&arr[--_right]);else if (arr[i] < key)Mysawp(&arr[i++],&arr[++_letf]);else i++;}Qsort(arr,left,_letf);Qsort(arr,_right,right);
}

⾮递归版本 ⾮递归版本的快速排序需要借助数据结构：栈--把每次划分出来的区间给存起来。

#include<queue>
//快排非递归版本
//快排升序
void Qsort1(int* arr, int left, int right)
{if (left >= right)return;std::queue<std::pair<int, int>> Q;Q.push({ left,right });while (!Q.empty()){int _letf = Q.front().first - 1, _right = Q.front().second + 1, i = Q.front().first;int key_index = rand() % (Q.front().second - Q.front().first + 1) + Q.front().first;int key = arr[key_index];while (i < _right){if (arr[i] > key)Mysawp(&arr[i], &arr[--_right]);else if (arr[i] < key)Mysawp(&arr[i++], &arr[++_letf]);else i++;}if(Q.front().first<_letf)//如果当前区间长度大于1Q.push({ Q.front().first,_letf });//把划分的区间存入队列if(_right<Q.front().second)Q.push({ _right,Q.front().second });if(!Q.empty())Q.pop();//删除已经交换过的区间}
}

3 归并排序

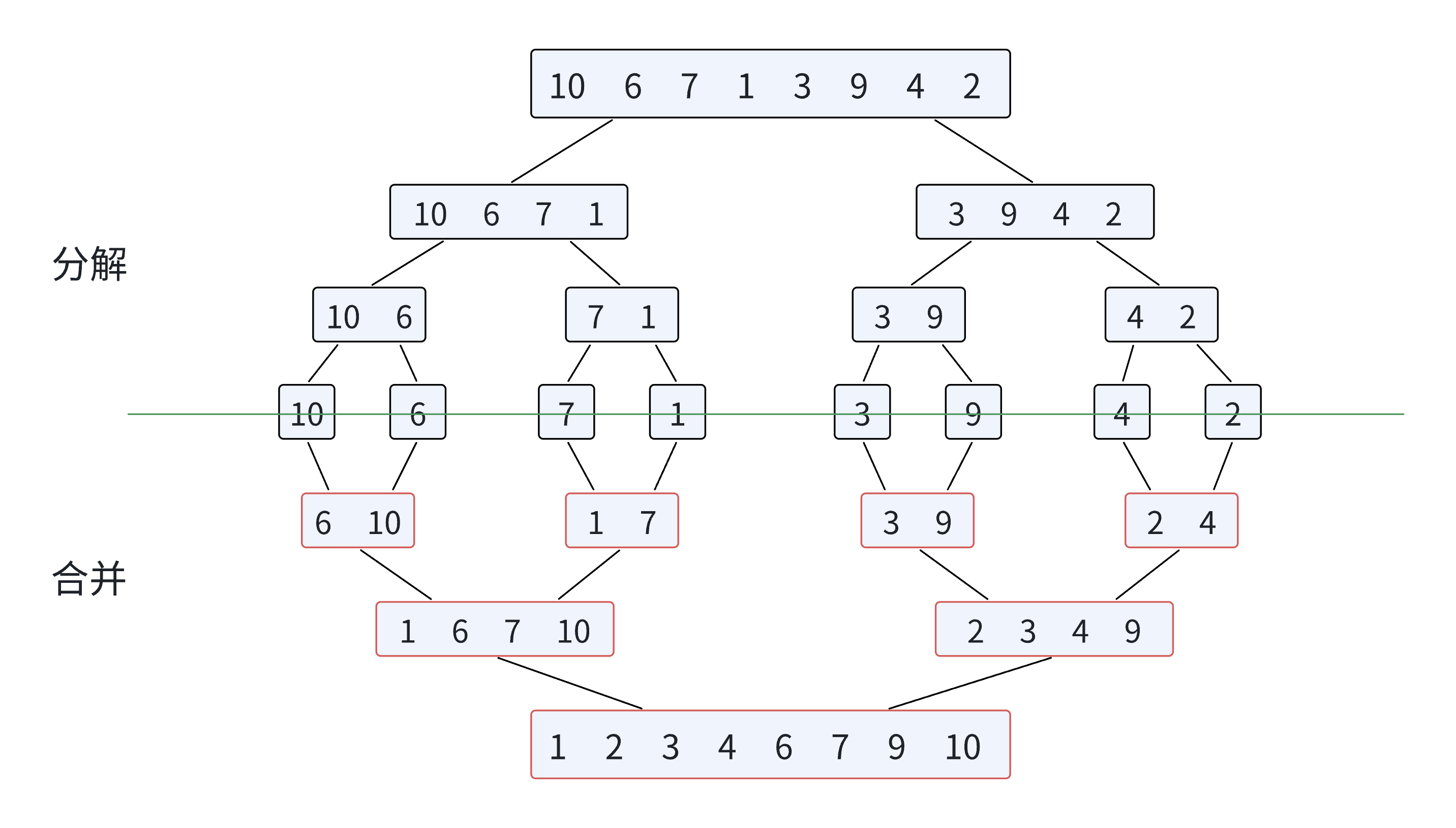
归并排序算法思想： 归并排序（MERGE-SORT）是建⽴在归并操作上的⼀种有效的排序算法,该算法是采⽤分治法（Divide and Conquer）的⼀个⾮常典型的应⽤。将已有序的⼦序列合并，得到完全有序的序列；即先使每个 ⼦序列有序，再使⼦序列段间有序。若将两个有序表合并成⼀个有序表，称为⼆路归并。归并排序核 ⼼步骤：合并两个有序数组。

https://leetcode.cn/problems/merge-sorted-array/submissions/656033777/

class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {vector<int> v;int cur1=0,cur2=0;while(cur1<m&&cur2<n){nums1[cur1]<nums2[cur2]?v.push_back(nums1[cur1++]):v.push_back(nums2[cur2++]);}while(cur1<m)v.push_back(nums1[cur1++]);while(cur2<n)v.push_back(nums2[cur2++]);nums1=v;}
};

int temp[100];
//归并排序
void mergesort(int* arr,int left,int right)
{if (left >= right)return;//如果数组长度小于等于1int mid = (left + right) / 2;//划分左右子数组mergesort(arr,left,mid);//递归继续划分区间mergesort(arr,mid+1,right);//合并两个有序子区间，从最短的区间开始合并两个即长度为1的子区间int cur1 = left, cur2 = mid + 1; int dex = left;//合并两个有序数组到辅助数组中去while (cur1 <= mid && cur2 <= right){arr[cur1] < arr[cur2] ? temp[dex++] = arr[cur1++] : temp[dex++] = arr[cur2++];}while (cur1 <= mid)temp[dex++] = arr[cur1++];while (cur2 <= right)temp[dex++] = arr[cur2++];for (int i = left; i <= right; i++)//排好序的数挪到原数组中去arr[i] = temp[i];}

5 ⾮⽐较排序--这个有意思

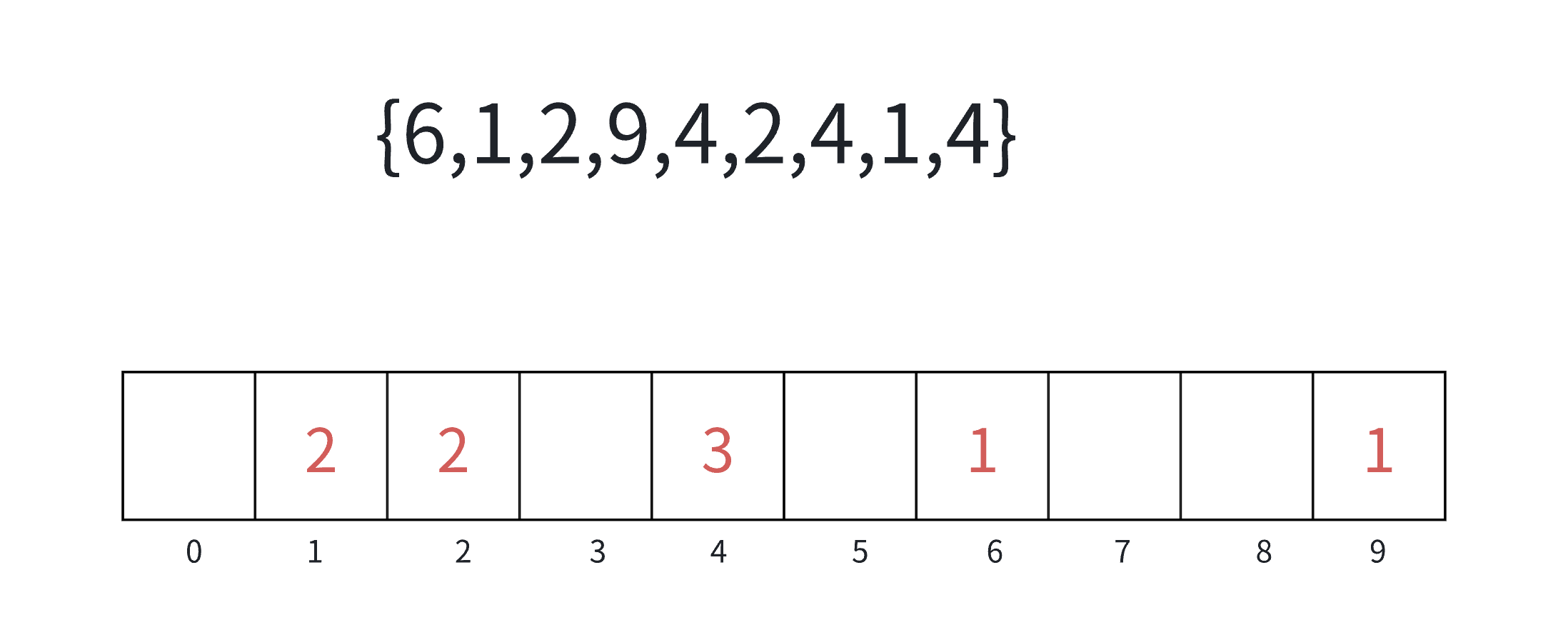
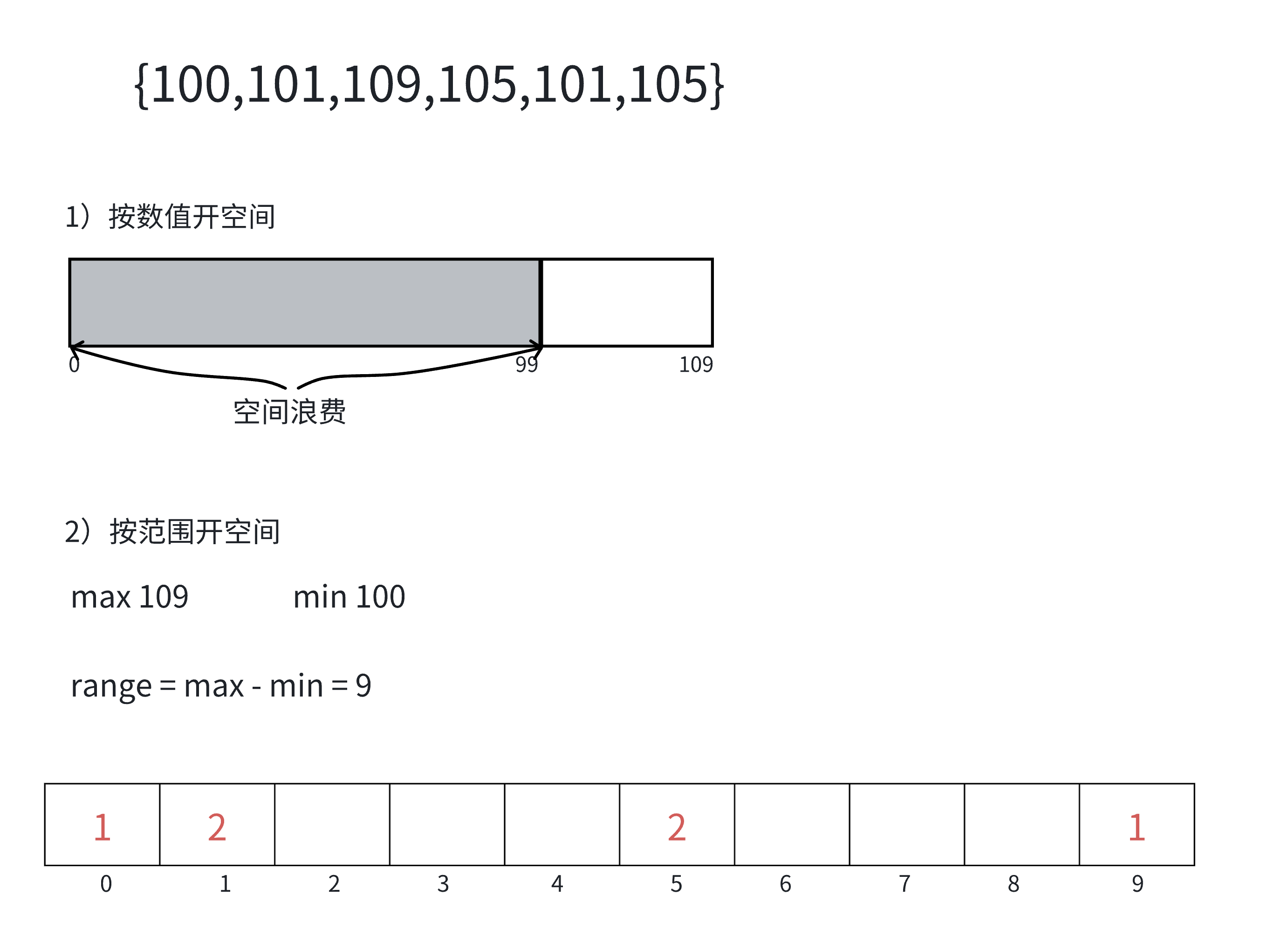
计数排序⼜称为鸽巢原理，是对哈希直接定址法的变形应⽤。操作步骤：

1）统计相同元素出现次数

2）根据统计的结果将序列回收到原来的序列中

void CountSort ( int * a, int n)
{
int min = a[0], max = a[0];
for ( int i = 1; i < n; i++)
{
if (a[i] > max)max = a[i];
if (a[i] < min)min = a[i];
}
int range = max - min + 1;
int * count = ( int *)malloc( sizeof ( int ) * range);
if (count == NULL)
{perror("malloc fail");return ;
}memset(count, 0, sizeof ( int ) * range);
// 统计次数
for ( int i = 0; i < n; i++)
{count[a[i] - min]++;`
}
// 排序
int j = 0;for ( int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}

计数排序的特性： 计数排序在数据范围集中时，效率很⾼，但是适⽤范围及场景有限。 时间复杂度：O(N + range) 空间复杂度： O(range) 稳定性：稳定

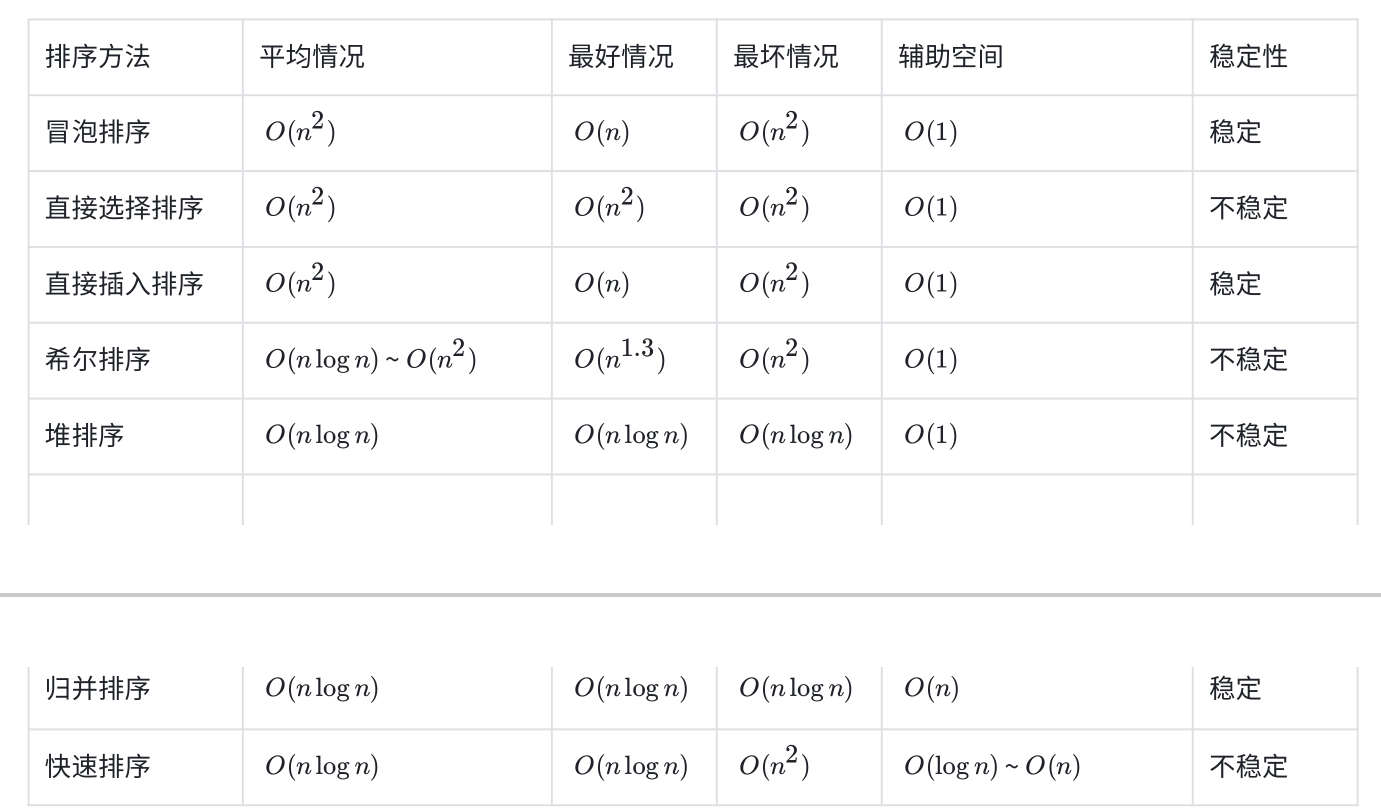
排序算法复杂度及稳定性分析

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的 相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，⽽在排序后的序列中，r[i]仍在r[j]之 前，则称这种排序算法是稳定的；否则称为不稳定的。

每天进步一点点，咱们要做长期主义者。