【数组】区间和

题目：

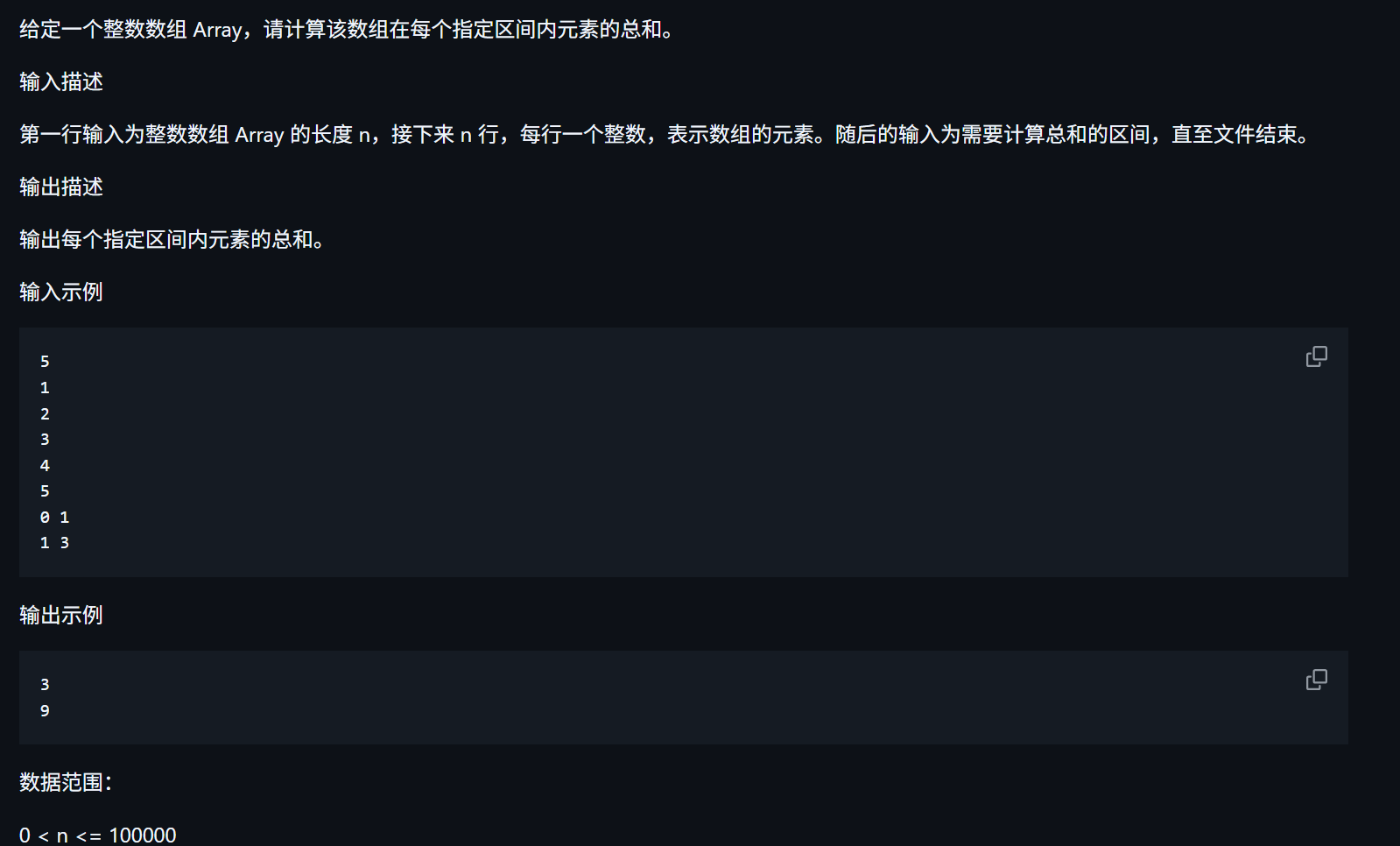
题目链接：58. 区间和（第九期模拟笔试）

方法：前缀和

思路：暴力求解就是每次读取区间，然后把区间内的数组依次相加。如果求和m次，每次都从头加到尾，时间复杂度为O(m*n)，如果m很大，时间复杂度会很大。如果用一个数组p专门保存子数组的和（前缀和）：p[i] = arr[0] + arr[1] + ....... + arr[i]，那么求区间[a,b]之间的和时，只需要p[b]-p[a-1]，时间复杂度为O(1)，相较于之前时间复杂度降为O(m)。

代码：

#include<iostream>
#include<vector>
using namespace std;int main()
{int n, a, b;scanf("%d", &n);vector<int> arr(n);vector<int> p(n);int presum = 0;//前缀和for(int i = 0;i<n;i++){scanf("%d", &arr[i]);presum += arr[i];p[i] = presum;}while(~scanf("%d %d", &a, &b)){int sum;if(a == 0)sum = p[b];elsesum = p[b] - p[a-1];printf("%d\n", sum);}return 0;
}