手把手带你推导“逻辑回归”核心公式

在机器学习中,逻辑回归是一种用于分类问题的模型,它的输出是一个概率值,表示某个样本属于某个类别的概率。
比如,在医疗诊断中,逻辑回归可以输出患者患病的概率。
逻辑回归不仅在医疗领域大显身手,还在金融、市场营销等众多领域发挥着重要作用。可以说,逻辑回归是数据分析的必备工具之一。
一、逻辑回归基础
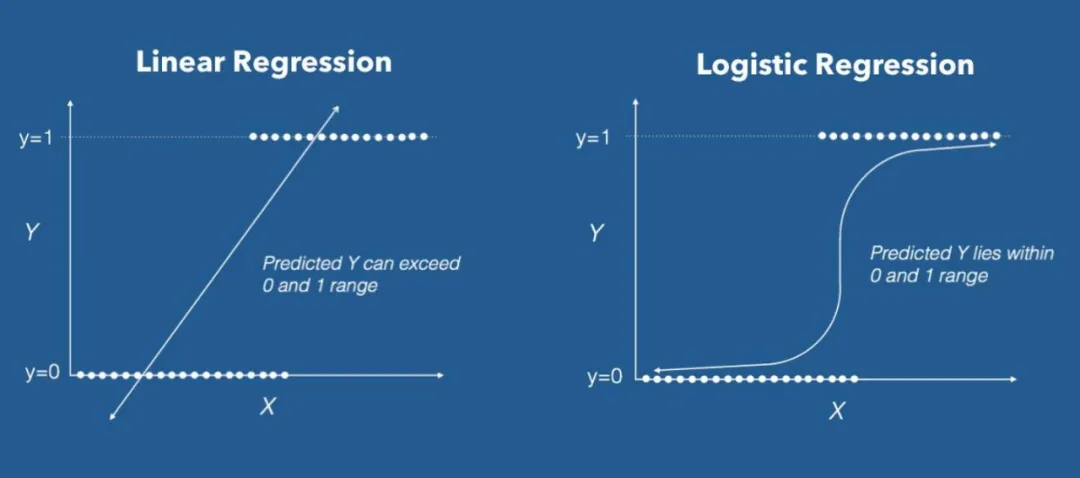
在介绍逻辑回归之前,我们先回顾一下线性回归。
线性回归是一种用于回归问题的模型,它的目标是找到一条直线,让这条直线尽可能地“贴合”数据点。
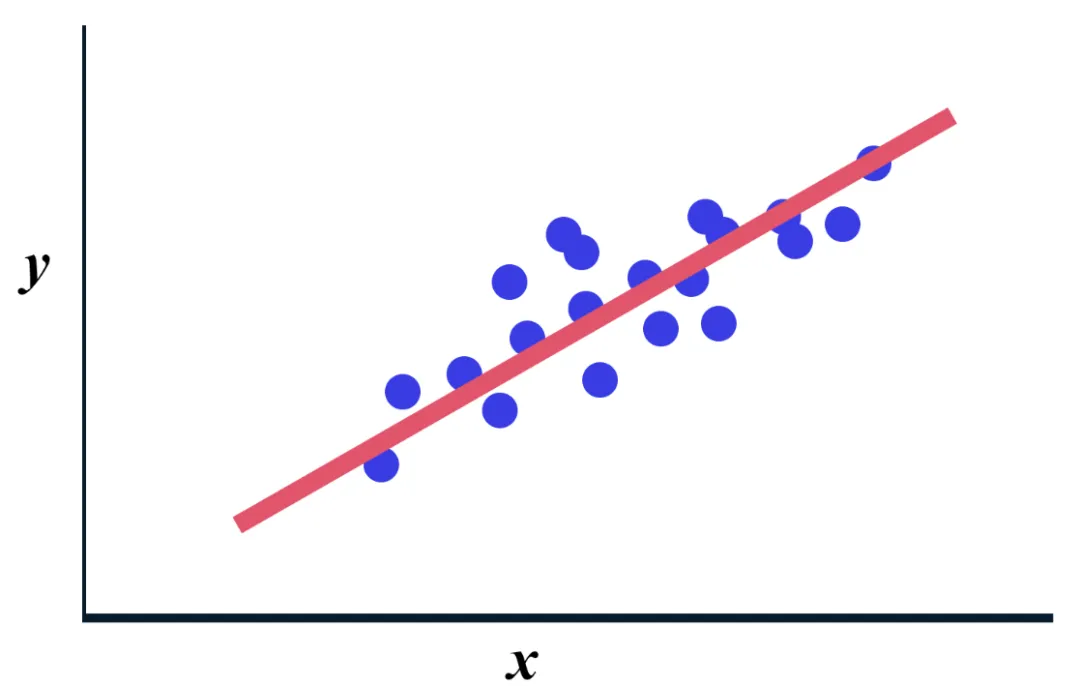
然而,线性回归在处理分类问题时会遇到一些问题。
比如,线性回归的输出是一个连续的数值,而分类问题需要的是一个离散的类别标签(如0或1)。
这就需要一种新的模型来解决分类问题,逻辑回归应运而生。
二、逻辑回归的核心公式
逻辑回归(Logistic Regression)是一种用于二分类问题的统计模型。
其核心公式是 Sigmoid 函数,也称为 Logistic 函数,它将线性回归的输出映射到 [0,1] 区间内,表示为概率。
逻辑回归的公式如下:
P(y=1∣x)=11+e−(β0+β1x1+⋯+βpxp) P(y = 1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_p)}} P(y=1∣x)=1+e−(β0+β1x1+⋯+βpxp)1
其中:
- P(y=1∣x)P(y = 1|x)P(y=1∣x) 是给定特征 xxx 的条件下,目标变量 yyy 等于 1 的概率。
- β0,β1,…,βp\beta_0, \beta_1, \ldots, \beta_pβ0,β1,…,βp 是模型的参数,其中 β0\beta_0β0 是截距项,β1,…,βp\beta_1, \ldots, \beta_pβ1,…,βp 是特征系数。
- x1,x2,…,xpx_1, x_2, \ldots, x_px1,x2,…,xp 是特征变量。
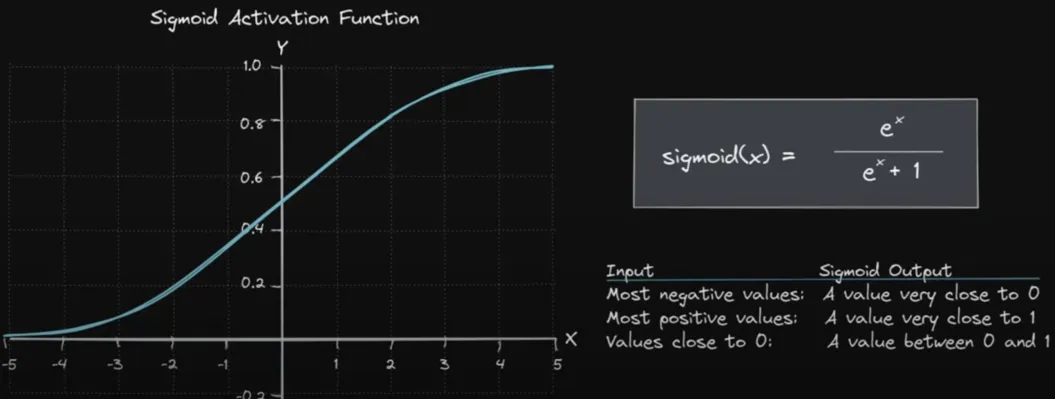
Sigmoid 函数 的图形是一个 S 形曲线,当线性组合 β0+β1x1+⋯+βpxp\beta_0 + \beta_1 x_1 + \cdots + \beta_p x_pβ0+β1x1+⋯+βpxp 趋向于正无穷时,P(y=1∣x)P(y = 1|x)P(y=1∣x) 趋向于 1;当线性组合趋向于负无穷时,P(y=1∣x)P(y = 1|x)P(y=1∣x) 趋向于 0。
逻辑回归的目标是找到参数 β0,β1,…,βp\beta_0, \beta_1, \ldots, \beta_pβ0,β1,…,βp,使得模型的预测概率与实际观测值之间的差异最小。
这通常可以通过极大似然估计(Maximum Likelihood Estimation, MLE)来实现,即最大化似然函数或等价地最小化负对数似然函数(Negative Log-Likelihood, NLL)。
对于一个包含 nnn 个独立样本的数据集 {(xi,yi)}i=1n\{(x_i, y_i)\}_{i=1}^n{(xi,yi)}i=1n,其中 yi∈{0,1}y_i \in \{0, 1\}yi∈{0,1},似然函数为:
L(β)=∏i=1nP(yi∣xi)=∏i=1n[P(yi=1∣xi)]yi[1−P(yi=1∣xi)]1−yi L(\beta) = \prod_{i=1}^{n} P(y_i|x_i) = \prod_{i=1}^{n} \left[P(y_i = 1|x_i)\right]^{y_i} \left[1 - P(y_i = 1|x_i)\right]^{1-y_i} L(β)=i=1∏nP(yi∣xi)=i=1∏n[P(yi=1∣xi)]yi[1−P(yi=1∣xi)]1−yi
负对数似然函数为:
NLL(β)=−∑i=1n[yilogP(yi=1∣xi)+(1−yi)log(1−P(yi=1∣xi))] NLL(\beta) = - \sum_{i=1}^{n} \left[ y_i \log P(y_i = 1|x_i) + (1 - y_i) \log (1 - P(y_i = 1|x_i)) \right] NLL(β)=−i=1∑n[yilogP(yi=1∣xi)+(1−yi)log(1−P(yi=1∣xi))]
通过最小化负对数似然函数,可以得到模型参数的极大似然估计。这通常使用梯度下降或其他优化算法来实现。
综上所述,逻辑回归的核心公式是 Sigmoid 函数,它将线性组合的输出映射到概率值。通过极大似然估计,可以找到最适合数据的模型参数。
三、逻辑回归公式推导
好的!接下来我从零开始,一步步推导逻辑回归的核心公式,特别是利用极大似然估计来求解参数的过程。

这个过程会涉及大量的数学推导,我会尽量详细地解释每一步🤗🤗🤗。
3.1 模型定义
逻辑回归是一种用于二分类问题的模型。假设我们有一组数据点 (xi,yi)(\mathbf{x}_i, y_i)(xi,yi),其中 xi\mathbf{x}_ixi 是特征向量,yi∈{0,1}y_i \in \{0, 1\}yi∈{0,1} 是目标变量。
逻辑回归模型的目标是预测 y=1y = 1y=1 的概率,即:
P(y=1∣x)=σ(βTx) P(y = 1|\mathbf{x}) = \sigma(\beta^T \mathbf{x}) P(y=1∣x)=σ(βTx)
其中,σ(z)\sigma(z)σ(z) 是 Sigmoid 函数:
σ(z)=11+e−z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
而 βTx\beta^T \mathbf{x}βTx 是线性部分:
βTx=β0+β1x1+β2x2+⋯+βnxn \beta^T \mathbf{x} = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n βTx=β0+β1x1+β2x2+⋯+βnxn
3.2 参数求解
逻辑回归通过极大似然估计来求解模型参数。
极大似然估计的基本思想是:找到一组参数,使得观测到的数据出现的概率最大。对于二分类问题,每个样本 iii 的似然函数可以表示为:
P(yi∣xi,β)=σ(βTxi)yi⋅(1−σ(βTxi))1−yi P(y_i|\mathbf{x}_i, \beta) = \sigma(\beta^T \mathbf{x}_i)^{y_i} \cdot (1 - \sigma(\beta^T \mathbf{x}_i))^{1-y_i} P(yi∣xi,β)=σ(βTxi)yi⋅(1−σ(βTxi))1−yi
这个公式的意思是:
- 如果 yi=1y_i = 1yi=1,则似然函数为 σ(βTxi)\sigma(\beta^T \mathbf{x}_i)σ(βTxi)。
- 如果 yi=0y_i = 0yi=0,则似然函数为 1−σ(βTxi)1 - \sigma(\beta^T \mathbf{x}_i)1−σ(βTxi)。
对于整个数据集,似然函数 L(β)L(\beta)L(β) 是所有样本似然函数的乘积:
L(β)=∏i=1nσ(βTxi)yi⋅(1−σ(βTxi))1−yi L(\beta) = \prod_{i=1}^{n} \sigma(\beta^T \mathbf{x}_i)^{y_i} \cdot (1 - \sigma(\beta^T \mathbf{x}_i))^{1-y_i} L(β)=i=1∏nσ(βTxi)yi⋅(1−σ(βTxi))1−yi
为了简化计算,我们通常取对数似然函数 ℓ(β)\ell(\beta)ℓ(β):
ℓ(β)=logL(β)=∑i=1n[yilogσ(βTxi)+(1−yi)log(1−σ(βTxi))] \ell(\beta) = \log L(\beta) = \sum_{i=1}^{n} \left[ y_i \log \sigma(\beta^T \mathbf{x}_i) + (1 - y_i) \log (1 - \sigma(\beta^T \mathbf{x}_i)) \right] ℓ(β)=logL(β)=i=1∑n[yilogσ(βTxi)+(1−yi)log(1−σ(βTxi))]
为了找到最优的参数 β\betaβ,我们需要最大化对数似然函数 ℓ(β)\ell(\beta)ℓ(β)。
3.3 优化方法
由于对数似然函数是一个非线性凸函数,我们通常可以使用数值优化算法,如梯度上升法(或梯度下降法)来求解。
- 梯度计算
我们需要计算对数似然函数 ℓ(β)\ell(\beta)ℓ(β) 对每个参数 βj\beta_jβj 的梯度:
∂ℓ(β)∂βj=∑i=1n[yiσ(βTxi)−1−yi1−σ(βTxi)]⋅∂σ(βTxi)∂βj \frac{\partial \ell(\beta)}{\partial \beta_j} = \sum_{i=1}^{n} \left[ \frac{y_i}{\sigma(\beta^T \mathbf{x}_i)} - \frac{1 - y_i}{1 - \sigma(\beta^T \mathbf{x}_i)} \right] \cdot \frac{\partial \sigma(\beta^T \mathbf{x}_i)}{\partial \beta_j} ∂βj∂ℓ(β)=i=1∑n[σ(βTxi)yi−1−σ(βTxi)1−yi]⋅∂βj∂σ(βTxi)
根据 Sigmoid 函数的导数:
∂σ(βTxi)∂βj=σ(βTxi)(1−σ(βTxi))⋅xij \frac{\partial \sigma(\beta^T \mathbf{x}_i)}{\partial \beta_j} = \sigma(\beta^T \mathbf{x}_i)(1 - \sigma(\beta^T \mathbf{x}_i)) \cdot x_{ij} ∂βj∂σ(βTxi)=σ(βTxi)(1−σ(βTxi))⋅xij
因此
∂ℓ(β)∂βj=∑i=1n[yi−σ(βTxi)]⋅xij \frac{\partial \ell(\beta)}{\partial \beta_j} = \sum_{i=1}^{n} \left[ y_i - \sigma(\beta^T \mathbf{x}_i) \right] \cdot x_{ij} ∂βj∂ℓ(β)=i=1∑n[yi−σ(βTxi)]⋅xij
- 梯度上升更新公式
根据梯度上升算法,参数的更新公式为:
βj=βj+α∂ℓ(β)∂βj \beta_j = \beta_j + \alpha \frac{\partial \ell(\beta)}{\partial \beta_j} βj=βj+α∂βj∂ℓ(β)
代入梯度:
βj=βj+α∑i=1n[yi−σ(βTxi)]⋅xij \beta_j = \beta_j + \alpha \sum_{i=1}^{n} \left[ y_i - \sigma(\beta^T \mathbf{x}_i) \right] \cdot x_{ij} βj=βj+αi=1∑n[yi−σ(βTxi)]⋅xij
其中,α\alphaα 是学习率,控制每次更新的步长。
通过上述步骤,我们可以找到最优的模型参数 β\betaβ,使得对数似然函数最大。最终的逻辑回归模型为:
P(y=1∣x)=σ(βTx) P(y = 1|\mathbf{x}) = \sigma(\beta^T \mathbf{x}) P(y=1∣x)=σ(βTx)
今天,我们从零开始,一步步推导了逻辑回归模型的核心公式。我们了解了逻辑回归的基本概念、核心公式、Sigmoid函数,以及极大似然估计。
但逻辑回归也有它的局限性,比如它只能处理线性可分问题,对于复杂的非线性关系就无能为力了。不过别担心,还有其他更强大的模型等着我们去探索,比如支持向量机、决策树等。
最后,希望你能动手实践一下逻辑回归模型,用真实的数据去感受它的魅力。
注:本文中未声明的图片均来源于互联网
