南京大学 LLM开发基础（一）前向反向传播搭建

主要围绕深度学习中 前向反向传播的搭建原理。

目录

1. 大语言模型导言

编码 +  Attention + 基本组件

Decoder-only 架构

2. 前向传播

3. 反向传播

Autograd -> 计算图 DAG

hw0：手搓一个线性层 Manual_Linear 并手动计算梯度

---

1. 大语言模型导言

https://njudeepengine.github.io/llm-course-lecture/2025/lecture1.html#1

硬件 -> 编程基础+深度学习框架 ->  神经网络架构 -> 模型的开发部署 -> 实际应用场景

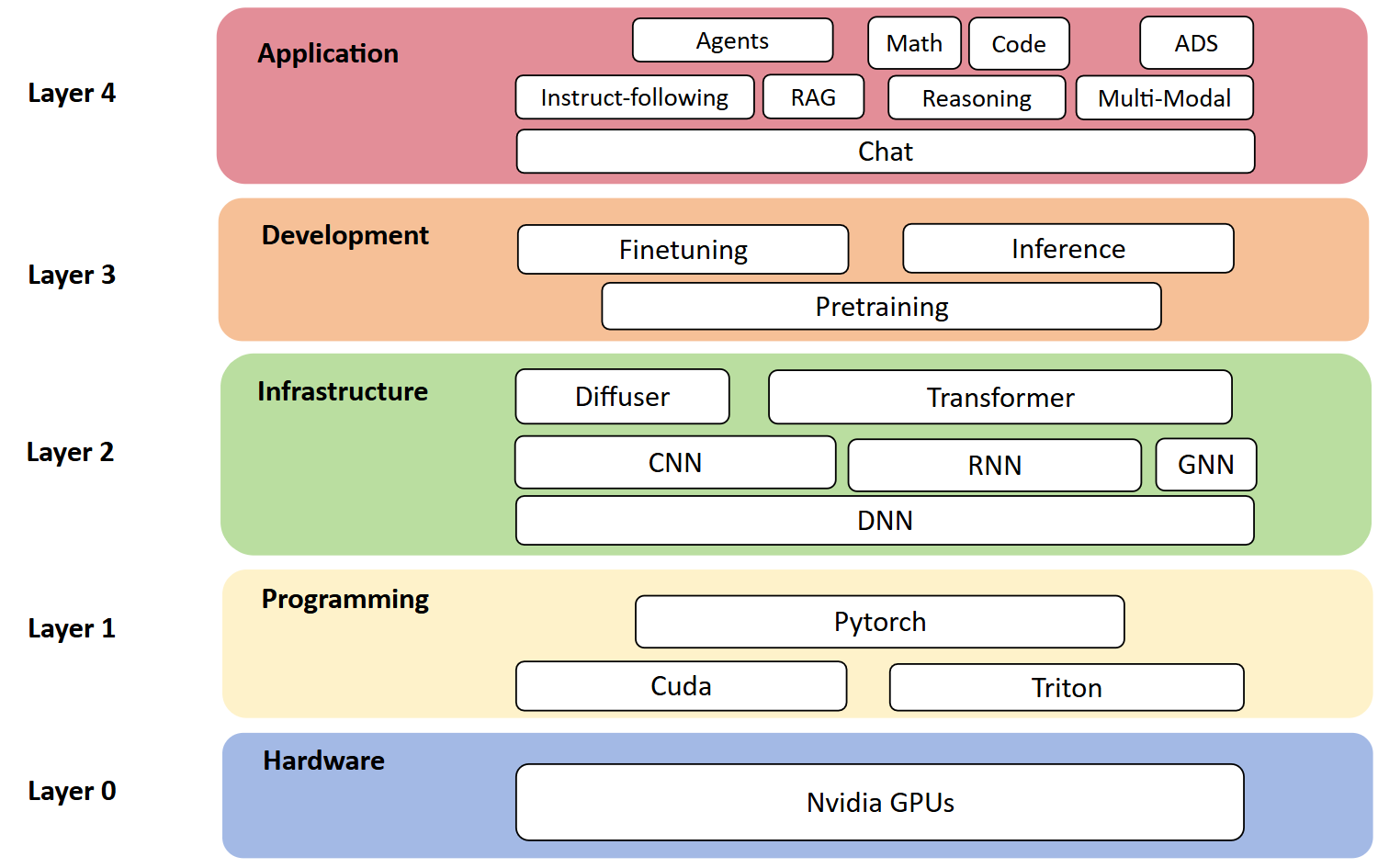
编码 +  Attention + 基本组件

语言模型，源于如何建模自然语言？比如如何解释“什么是南京大学”。

把“南京大学”输入模型，就需要一个编码器encoder去转换这四个字。

如何认识单词？编码：one-hot编码, word2vec（上下文完形填空训练）, tokenization

经典向量投射例子 king - man = queen - woman

如何理解语言？多次 Attention 算两两之间字词的意思关系。

基础组件（积木）：残差(residual), layernorm, attention, softmax, positional embedding

大规模训练 多卡多机：需要分布式运行

Decoder-only 架构

在BERT时代 虽然上下文完形填空和生成过程有些矛盾，但当时有一些训练效果（比只预测下文好训练 decoder-only每个位置所能接触的信息比其他架构少，要预测下一个token难度更高，但上限更高）。

后来模型参数量提高后 显卡和数据比较多后 GPT能力大大增强。

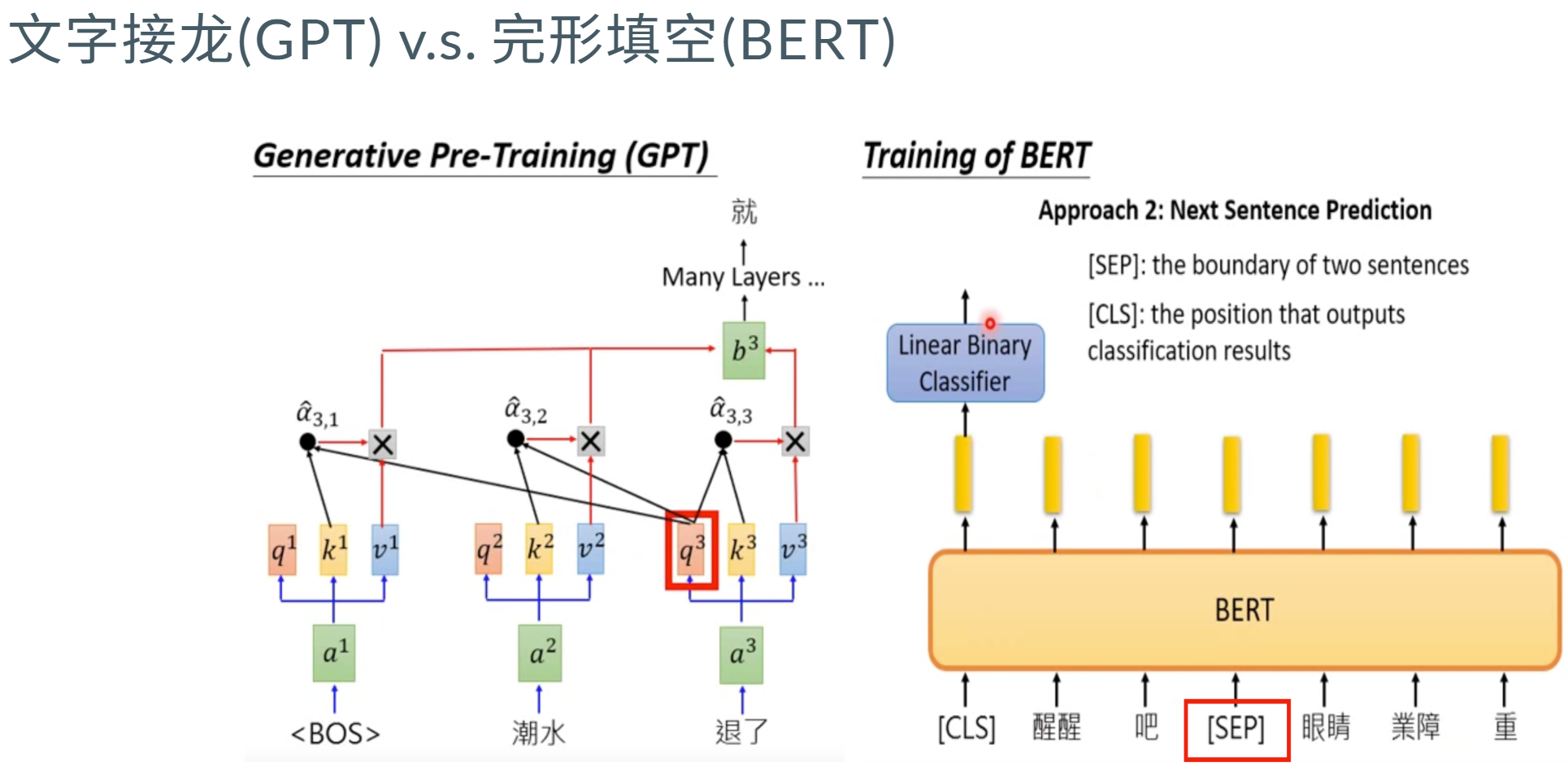
目前生成能力 还是以 GPT 为代表的Decoder-only架构为主。

下游任务 zero/few-shot 泛化性能好。

Encoder的双向注意力会存在低秩问题，这可能会削弱模型表达能力，就生成任务而言，引入双向注意力并无实质好处。而Encoder-Decoder架构之所以能够在某些场景下表现更好，大概只是因为它多了一倍参数。所以，在同等参数量、同等推理成本下，Decoder-only架构就是最优选择了。

2. 前向传播

前向传播：从输入到输出，计算预测结果

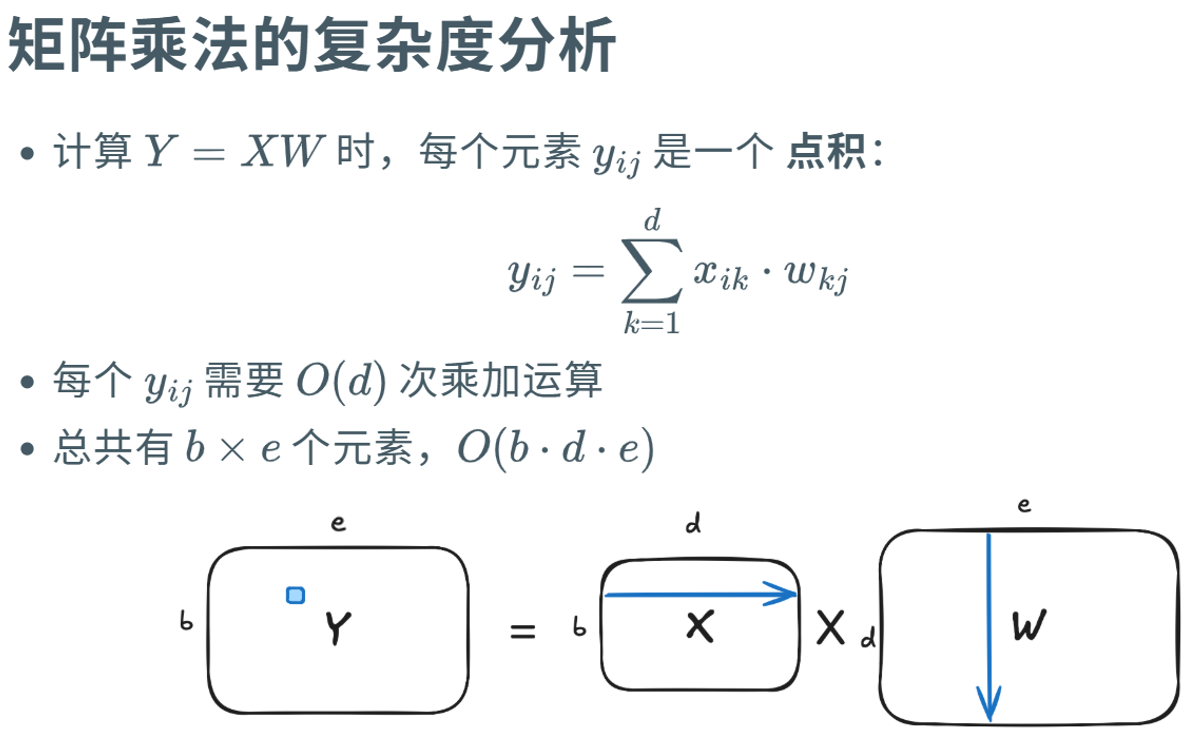
矩阵乘法 与 元素乘法

# 矩阵乘法
y = x@w
y = x.matmul(w)
y = torch.matmul(x, w)# 元素乘法
y = x*w
y = x.mul(w)
y = torch.mul(x, w)

层的堆叠  x是128个样本 每个样本20维度；m1 20->30    m2 30->40.

m1 = nn.Linear(20, 30)
m2 = nn.Linear(30, 40)
x = torch.randn(128, 20)
y1 = m1(x)
y2 = m2(y1)

3. 反向传播

https://njudeepengine.github.io/llm-course-lecture/2025/lecture3.html#1

反向传播：从输出到输入，计算梯度，更新参数

核心思想：通过链式法则计算复合函数的导数

• 目标：找到使损失函数最小的参数  Y=XW 找那个W
• 方法：梯度下降，需要计算损失函数对每个参数的梯度
• 挑战：深度学习模型是复合函数，直接计算梯度困难
• 解决：反向传播算法，针对优化目标 J(θ) 按层“回退”，一层一层求偏导

很多层进行 复合函数

Autograd -> 计算图 DAG

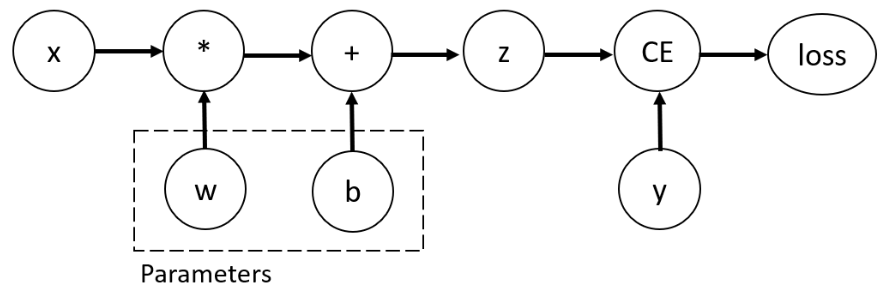
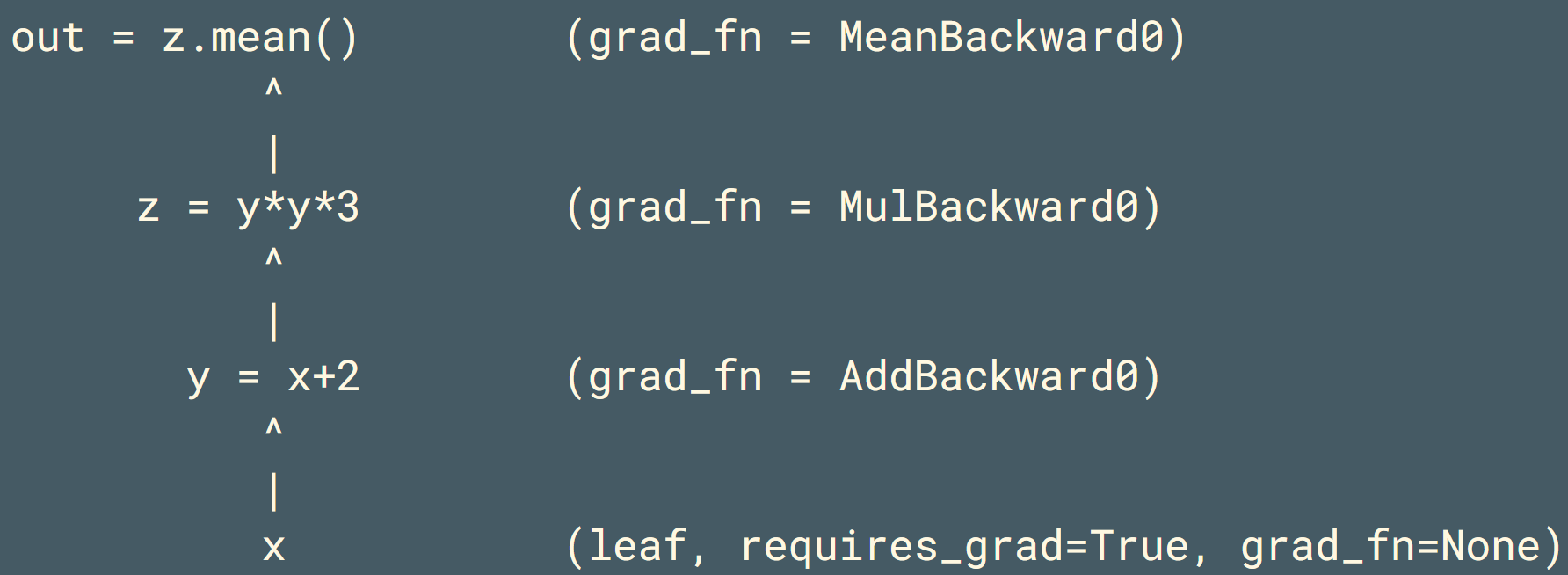
非叶子节点 记录 grad_fn 描述生成该tensor的运算方式，即描述反向传播时如何计算梯度。

print tensor 时既包含张量值 也包含grad_fn。

import torchx = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()print(x.grad_fn)  # None，因为x是叶子张量
print(y.grad_fn)  # <AddBackward0>，表示加法操作
print(z.grad_fn)  # <MulBackward0>，表示乘法操作
print(out.grad_fn) # <MeanBackward0>，表示 mean 操作

Autograd的无感知使用

backward() 启动反向传播计算；之前清空梯度；之后更新梯度

optimizer = torch.optim.SGD(net.parameters(), lr=0.01)for epoch in range(100):# 前向传播y = net(x)loss = criterion(y, target)# 反向传播optimizer.zero_grad()  # 清零梯度loss.backward()        # 计算梯度optimizer.step()       # 更新参数

with torch.no_grad(): 上下文内不记录计算图，不分配 grad_fn/中间量，因此这些计算不参与 loss.backward()。

用途： 纯推理/验证（配合 model.eval()）。

比如用于模型蒸馏 小模型学大模型的输出。两者都要前向操作 然后更新小模型需要grad 大模型不需要grad

hw0：手搓一个线性层 Manual_Linear 并手动计算梯度

A0 Onboarding | LLM-Assignment-Doc

我们进一步定义一个标量损失函数 loss = (Y ** 2).sum()

首先初始化 权重矩阵W（也要同步给测试的输入） W_grad 梯度初始化为零矩阵。

class ManualLinear:def __init__(self, in_dim, out_dim, device=None, dtype=torch.float32):# 初始化权重矩阵 W，随机值，形状为 [输入维度, 输出维度]# requires_grad=False 是关键！因为我们手动计算梯度，不需要autograd帮忙self.W = torch.randn(in_dim, out_dim, device=device, dtype=dtype, requires_grad=False)# 初始化一个全0的张量，用来存储我们手动计算出的权重梯度 dL/dWself.W_grad = torch.zeros_like(self.W)

进一步，完整的 forward 过程即：

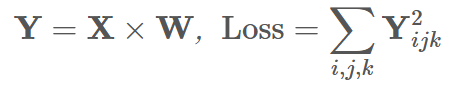
使用 Y = X @ w     @进行矩阵乘法

def forward(self, x):# 保存输入x，反向传播计算 dL/dW = X^T @ (dL/dY) 时会用到！self.input = xreturn x @ self.W

backward 的计算过程：

首先关于梯度/偏导 需要满足矩阵shape一致性：

分母布局求导（主流深度学习框架默认） 每行为每个分母对应梯度

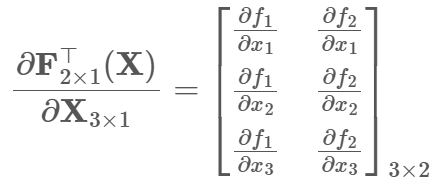
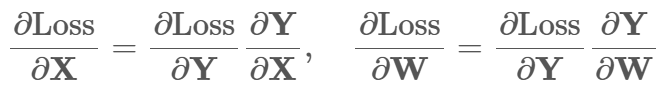
此外 由于乘法求导等于转置 可进一步化为

        

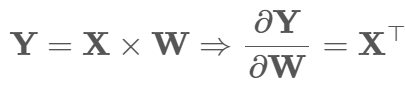
在实现的过程中 由于输入x 是三维的；第一个维度为批量大小b，所以需要合并前两维（展平）

def backward(self, grad_output):# grad_output 就是从后面一层传回来的梯度 dL/dY, 形状是 [b, h, e]# 获取输入X的维度，以便后续reshape操作b, h, d = self.input.shape# 我们需要把 batch 和 h 维度合并，看作一个大的“样本”维度。# 将输入X从 [b, h, d] 重塑为 [b*h, d]# 这相当于把多个样本在批次维度上拼接起来x_flat = self.input.reshape(-1, d)# 同样，将上游梯度 grad_output 从 [b, h, e] 重塑为 [b*h, e]grad_out_flat = grad_output.reshape(-1, self.W.shape[1])# 现在执行矩阵乘法： [d, b*h] @ [b*h, e] -> [d, e]# x_flat.T 的形状是 [d, b*h]# grad_out_flat 的形状是 [b*h, e]# 它们相乘的结果正好是 [d, e]，和权重W的形状一致！# 这个操作在数学上等价于：对batch中的每一个样本计算 x_i^T @ (dL/dY_i)，然后把所有结果加起来。self.W_grad = x_flat.T @ grad_out_flatgrad_input = grad_output @ self.W.Treturn grad_input # 将梯度返回，用于前一层的反向传播

step 根据学习率 梯度下降更新；减去学习率lr * 梯度W

# 梯度下降更新
def step(self, lr=1e-2):self.W -= lr * self.W_grad

Manual_Linear调用 Y**2 对 Y 偏导就是 2Y；作为上一层的grad_output 送给backward

manual_linear = ManualLinear(d, e, device=device, dtype=dtype)
y_manual = manual_linear.forward(x)
loss_manual = y_manual.pow(2).sum()
grad_output = 2 * y_manual
grad_input_manual = manual_linear.backward(grad_output)

使用pytest 比较与 PyTorch AutogradLinear 自动求导机制与手动计算的一致性。

手动计算时 randn生成的W权重复制过来

.requires_grad 梯度跟踪的X 和 Y 随后才能用 .grad

计算平方和损失      .backward()自动计算梯度； 得到对X和W的梯度

三个assert断言 前向传播结果，对X和W的梯度

# 创建一个使用PyTorch自动求导的线性层实例
autograd_linear = AutogradLinear(d, e, device=device, dtype=dtype)# 关键步骤：确保两个模型的初始权重完全一致，才能进行公平比较
with torch.no_grad():# 将手动线性层的权重数值复制到自动求导线性层的权重中autograd_linear.W.copy_(manual_linear.W)# 准备用于自动求导的输入数据
# .requires_grad_()：要求对这个新张量进行梯度跟踪，这样autograd才能计算关于它的梯度x_autograd = x.clone().detach().requires_grad_()y_autograd = autograd_linear(x_autograd)  # x->yloss_autograd = y_autograd.pow(2).sum()  # 平方和损失loss_autograd.backward() # 反向传播 自动计算梯度grad_input_autograd = x_autograd.grad # X梯度grad_weight_autograd = autograd_linear.W.grad # W梯度# ========== 验证阶段：对比手动实现 vs 自动求导 ==========# 断言1：验证前向传播结果是否一致
torch.testing.assert_close(y_manual, y_autograd, rtol=1e-4, atol=1e-4)# 断言2：验证输入梯度是否一致
# 检验手动实现的 dL/dx = grad_output @ W^T 公式是否正确
torch.testing.assert_close(grad_input_manual, grad_input_autograd, rtol=1e-4, atol=1e-4)# 断言3：验证权重梯度是否一致
# 检验手动实现的 dL/dW = x^T @ grad_output 公式是否正确
torch.testing.assert_close(manual_linear.W_grad, grad_weight_autograd, rtol=1e-4, atol=1e-4)