当前位置：首页 > news >正文

有趣的数学贝塞尔曲线和毕加索

news 2025/9/10 13:04:04

毕加索的狗

巴勃罗·毕加索的一些作品就是一些简单的线条画。

比较多的是关于动物的作品：猫头鹰、骆驼、蝴蝶等。还有下面这件名为“狗”的作品。

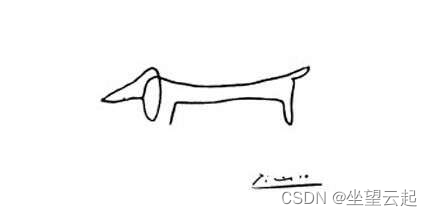
这些画非常简单，有很多人喜欢，但是也有很多人是一点都不喜欢，我也是但是的一部分。但是毕加索风格的线条画视看起来很像贝塞尔曲线。

这些画作极其简洁，却又给人一种深刻的印象。它们给人的印象是设计和绘制起来非常简单。一笔一画，一个潦草的签名，但却是一幅"杰作"！

我是很难理解，这是什么杰作？

事实上，艺术圈的人都说毕加索的创作过程非常深刻（其实我一直都很阴暗的思考这种事，每个圈子的人都会努力的抬高自己的圈子的地位或者说品味）。

例如，在1945年至1946年间，毕加索创作了一系列十一幅素描（实际上是石版画），展现了他对公牛的演绎过程。前几幅画或多或少栩栩如生，但随着系列的进展，看到公牛被提炼出它的本质，最终的画作仅用了十行线条。沿途我们看到的公牛素描与毕加索的其他一些作品很相似。

有一种显而易见的方法可以将毕加索风格的线条画视为数学对象，而这本质上就是贝塞尔曲线。让我们来研究一下贝塞尔曲线背后的理论，所涉及的数学知识不需要任何背景知识，只需要一些基本的代数和多项式知识，我们可以使用一个非常简单的贝塞尔曲线绘制算法，并用 JavaScript 实现它，并将毕加索的一幅线条画重新创建为一系列贝塞尔曲线。

贝塞尔曲线和参数化

打个比方，曲线板（French curve）是手工素描时用的一种实物模板，用来辅助手绘出平滑的曲线。沿着这些曲线的任意部分边缘去画，通常得到的不是函数图像那样的东西。显然，我们得稍微拓展下对曲线的概念理解。问题是，很多数学领域对曲线的定义都不一样。我们要研究的曲线叫贝塞尔曲线，它是单参数多项式平面曲线里的一种特殊类型。这听起来有点绕，但意思是整条曲线能用两个多项式来确定数值：一个算 x 值，一个算 y 值。这两个多项式共用同一个变量，我们把这个变量叫做 t，而且 t 是实数。

举个例子就好理解了。我们选两个简单的多项式，比如 x (t) = t²，y (t) = t³。要是想找这条曲线上的点，我们可以选 t 的值，再把它代入这两个方程里。比如，代入 t = 2，就得到曲线上的点 (4, 8)。把所有这样算出的值画出来会得到一条曲线，但它肯定不是函数的图形。

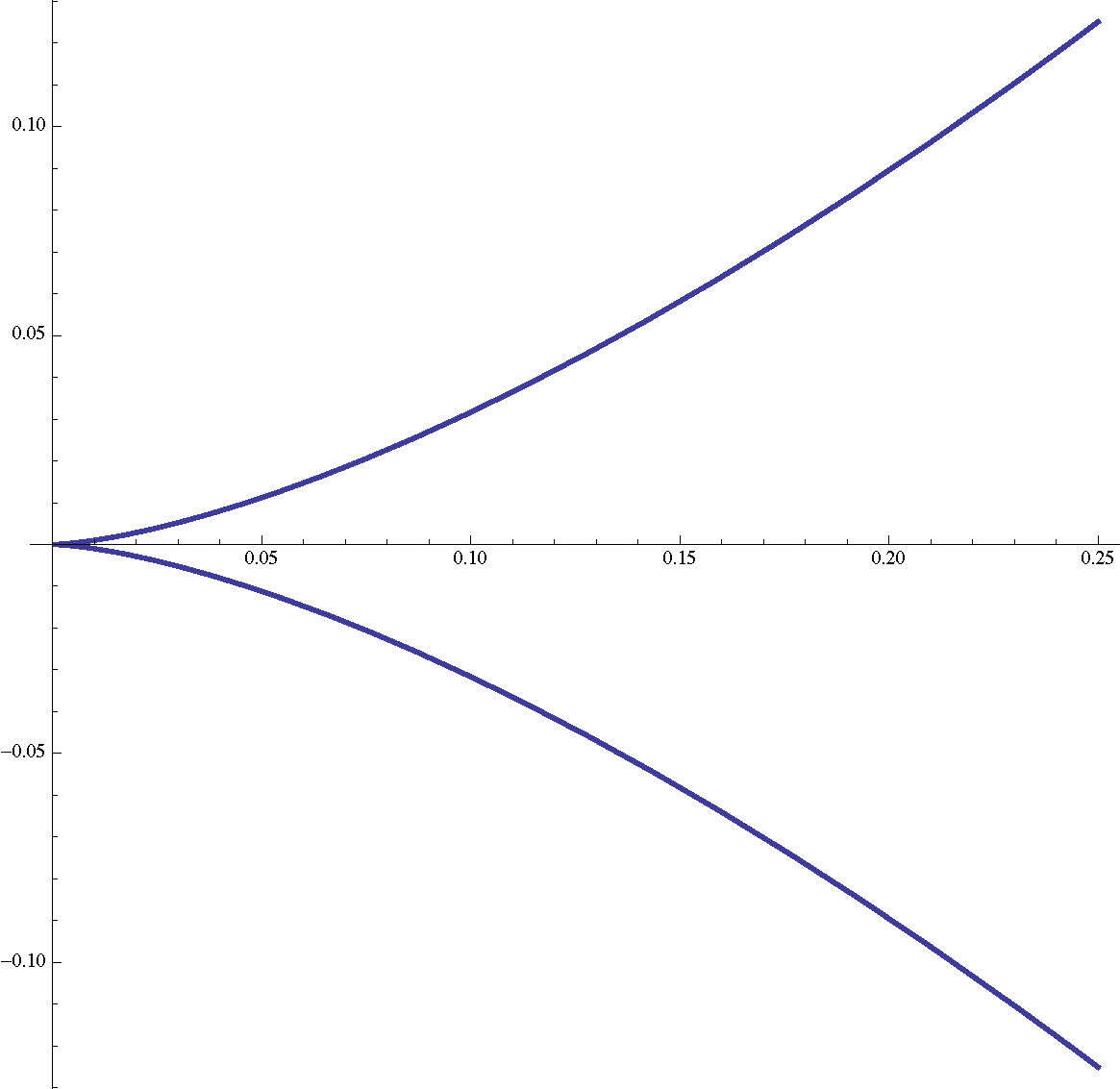
但很明显，任何单变量函数 $f(x)$ 都能写成这种参数形式：只要选 $x(t) = t$ ，再选 $y(t) = f(t)$ 就行。所以，这些实际上是比常规函数更通用的东西（不过咱们在这篇文章里只讨论多项式）。

快速复习一下，单参数多项式平面曲线的定义是：一对关于同一个变量t的多项式 $x(t)$ 和 $y(t)$ 。有时候，如果我们想把整个 “小工具” 当成一个整体来表示，我们可以把t拿过来，把它们写成向量的x和y分量。就用前面x(t) = t²、y(t) = t³的例子，我们可以把它重新写成：

${f}(t) = (0, 1)t³ + (1, 0)t²$

这里的系数是平面上的点（和向量是一回事），我们用粗体字母f来表示这个函数，就是为了强调它的输出是一个点。学线性代数的人可能会发现，这样的多项式对构成了一个向量空间，还能进一步把它们组合成(0, t³) + (t², 0) = (t², t³)。但对我们来说，把点当成单个多项式的系数其实更方便。

我们还把注意力限定在单参数多项式平面曲线上，这里变量t允许的取值范围是从 0 到 1。这看起来像是个挺别扭的限制，但实际上，每一条有限的单参数多项式平面曲线都能这么写（具体怎么实现的细节我们就不展开多讨论了）。为了简洁，接下来我们把 “单参数多项式平面曲线（变量t取值范围从 0 到 1）” 就简单称为 “曲线”。

现在我们能用曲线做些很酷的事。比如说，给定平面上任意两个点 $P = (p_1, p_2)$ 、 $Q = (q_1, q_2)$ ，我们可以把它们之间的直线描述成这样的曲线： ${L}(t) = (1 - t)P + tQ$ 。确实，当t = 0时， ${L}(t)$ 就是点P；当t = 1时，就是点Q，而且这个方程里的变量就是t。

另外（不用过多涉及微积分的细节）， ${L}(t)$ 是以 “单位速度” 从P到Q的。换句话说，我们可以认为 ${L}(t)$ 描述的是粒子从P运动到Q的过程，随着时间推移，当时间过了1/4，粒子就走了四分之一的路程；时间过了1/2，粒子就到中间位置了，诸如此类。（没有单位速度的直线例子，比如 $(1 - t²)P + t²Q$ 。

更一般地说，我们再添加第三个点R，就可以描述一条从P到R、中间由Q“引导” 的曲线。“引导” 点这个概念有点抽象，但计算起来并不难。我们不是想以恒定速度从一个点移到另一个点，而是想以恒定速度从一条线移到另一条线。也就是说，先分别描述从 $P \to Q$ 的 ${L}_1$ 和从 $Q \to R$ 的 ${L}_2$ 。然后，由Q“引导” 的曲线可以写成： ${F}(t) = (1 - t)\mathbf{L}_1(t) + t\mathbf{L}_2(t)$ 把这些都展开计算，就能得到公式： ${F}(t) = (1 - t)^2 P + 2t(1 - t)Q + t^2 R$

可以用粒子运动的情况来理解。在曲线刚开始的地方，t的值很小，所以此时我们非常靠近 ${L}_1$ 这条线。随着时间慢慢推移， ${F}(t)$ 会沿着 ${L}_1(t)$ 和 ${L}_2(t)$ 之间的连线移动，而 ${L}_1(t)$ 和 ${L}_2(t)$ 本身也在移动。这样的运动过程就描绘出了一条曲线，大致就是这样的情形。

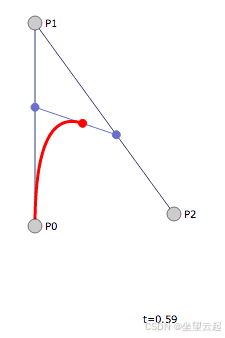
查看演示，它完美地表达了数学思想，你可以拖动三个点来观察最终曲线的变化。

贝塞尔曲线的整个概念是对这个原理的概括：给定平面上的一个点列( $P_0, \dots, P_n$ )，我们想要描述一条从第一个点到最后一个点的曲线，并且在这中间由剩下的点 “引导”。贝塞尔曲线就是这种曲线（单参数多项式平面曲线）的一种实现，它是我们上面所描述内容的归纳延续：我们以单位速度，从由第一个点定义的贝塞尔曲线，经过点列中第n - 1个点所定义的曲线，最终到第n - 1个点。基准情况是直线段（或者，如果你愿意，也可以是单个点）。正式来说，

定义：给定平面上的点列 $P_0, \dots, P_n$ ，我们递归地定义 $n - 1$ 次贝塞尔曲线为 \ $\begin{aligned} \mathbf{B}_{P_0}(t) &= P_0 \\\ \mathbf{B}_{P_0 P_1 \dots P_n}(t) &= (1-t)\mathbf{B}_{P_0 P_1 \dots P_{n-1}} + t \mathbf{B}_{P_1P_2 \dots P_n}(t) \end{aligned}$ 我们把 $P_0, \dots, P_n$ 称为控制点。

虽然在两条低次贝塞尔曲线之间以单位速度行进的概念才是问题的核心（并且能让我们获得真正的计算洞察力），但我们可以把所有这些（通过二项式系数公式）相乘，从而得到一个明确的公式。这个公式是：

$\displaystyle \mathbf{B}_{P_0 \dots P_n} = \sum_{k=0}^n \binom{n}{k}(1-t)^{nk}t^k P_k$

例如，带有控制点 $P_0, P_1, P_2, P_3$ 的三次贝塞尔曲线，会有这样的方程： $\displaystyle (1-t)^3 P_0 + 3(1-t)^2t P_1 + 3(1-t)t^2 P_2 + t^3 P_3$

高次贝塞尔曲线的几何描绘可能相当复杂。例如，下图是一条五次贝塞尔曲线（有六个控制点）。

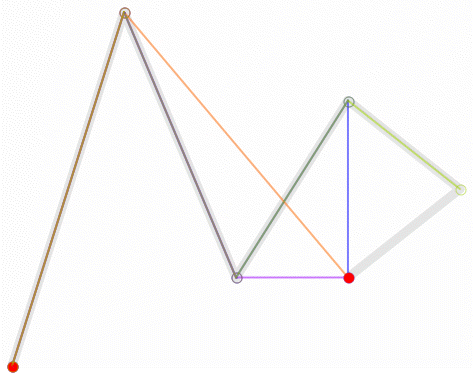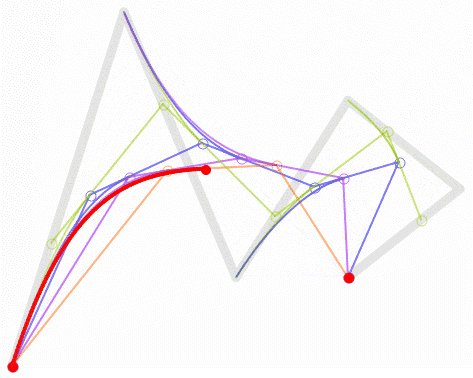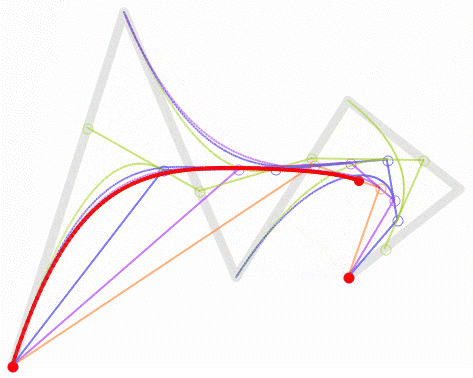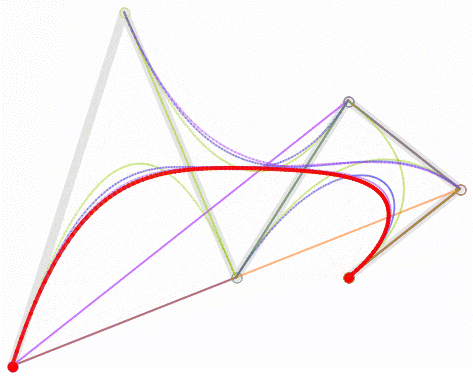
额外画出来的线段体现了曲线的递归特点。最基础的是绿点，它们在各个控制点之间移动。接着，蓝点沿着绿点之间的线段移动，粉点沿着蓝点之间的线段移动，橙点沿着粉点之间的线段移动，最后，红点沿着橙点之间的线段移动。

要是看不到这种递归的结构（只看曲线本身），我们很难想到该怎么用这些来实际计算。不过，就像我们接下来会看到的，画贝塞尔曲线的算法是很自然、容易理解的。

咱们要搞清楚怎么只靠画直线的本事，把贝塞尔曲线画到屏幕上。为了简单些，就先聚焦在三阶（三次）贝塞尔曲线。实际上，每条贝塞尔曲线都能通过递归的方式，写成三次曲线的组合。而且在实际应用里，三次曲线在计算效率和表达能力之间做得比较平衡。这里的所有代码都是用 JavaScript 写的。

三次贝塞尔曲线在程序里可以用四个点的列表来表示。比如说，像这样 var curve = [[1,2], [5,5], [4,0], [9,3]]; 。

大多数图形库（包括 HTML5 Canvas 标准）都有一个绘图的基本功能，能根据给定的四个点的列表，输出贝塞尔曲线。但假设我们没有这样的函数，假设我们只能画直线，那该怎么绘制出近似的贝塞尔曲线呢？要是有这样的算法（确实是有的，咱们马上就能看到），那我们就能让近似的曲线特别精细，精细到在视觉上和真正的贝塞尔曲线几乎分不出来。

贝塞尔曲线有个关键的特性，能让我们想出这样的算法，具体是这样的：任意一条三次贝塞尔曲线 B 都能分成两部分，这两部分首尾相连，合起来描绘的就是同一条曲线 B。

咱们来看看具体咋操作。B(t) 是有着控制点 $P_0, P_1, P_2, P_3$ 的三次贝塞尔曲线，假设我们想把它分成两半。咱们留意到，当代入 1/2时，也就是：

$\displaystyle \mathbf{B}(1/2) = \frac{1}{2^3}(P_0 + 3P_1 + 3P_2 + P_3)$

另外，咱们的递归定义给出了一种用次数更低的曲线来计算点的方法。不过当这些曲线用 \1/2 来计算时，它们的公式也很容易写出来。用图展示如下：

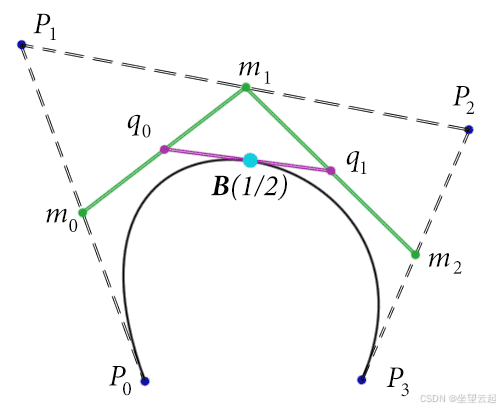
绿点代表一次曲线，粉点代表二次曲线，蓝点代表三次曲线。我们发现，因为每条曲线的求值点是 t = 1/2，所以这些点里的每一个都能说成是我们已经知道的点的中点。所以 $m_0 = (P_0 + P_1) / 2, q_0 = (m_0 + m_1)/2$ ，以此类推。

实际上，我们想要的两条曲线的分叉点就是由这些点确定的。也就是说，曲线的 “左” 半部分是由曲线 $\mathbf{L}(t)$ 来表示的，它的控制点是 $P_0, m_0, q_0, \mathbf{B}(1/2)$ ；而 “右” 半部分 $\mathbf{R}(t)$ 的控制点是 $\mathbf{B}(1/2), q_1, m_2, P_3$ 。

我们怎么能完全确定这些是相同的贝塞尔曲线呢？我们可以通过一些复杂的代数运算来比较它们是否相等。但要注意，因为 $\mathbf{L}(t)$ 只走了 $\mathbf{B}(t)$ 一半的路程，所以检查它们是否相同就相当于比较 $\mathbf{L}(t)$ 和 $\mathbf{B}(t/2)$ ，因为 t 的范围是从 0 到 1， $t/2$ 的范围就是从 0 到 1/2。同样地，我们可以比较 $\mathbf{B}((t+1)/2)$ 和 $\mathbf{R}(t)$ 。

代数运算挺复杂的，但能做到。

不管那些了，反正我们现在有了一个算法，可以将三次贝塞尔曲线（或任何贝塞尔曲线）分割成两部分。


function midpoints(pointList) {var midpoint = function(p, q) {return [(p[0] + q[0]) / 2.0, (p[1] + q[1]) / 2.0];};var midpointList = new Array(pointList.length - 1);for (var i = 0; i < midpointList.length; i++) {midpointList[i] = midpoint(pointList[i], pointList[i+1]);}return midpointList;
}function subdivide(curve) {var firstMidpoints = midpoints(curve);var secondMidpoints = midpoints(firstMidpoints);var thirdMidpoints = midpoints(secondMidpoints);return [[curve[0], firstMidpoints[0], secondMidpoints[0], thirdMidpoints[0]],[thirdMidpoints[0], secondMidpoints[1], firstMidpoints[2], curve[3]]];
}function drawSegments(curve, context) {context.beginPath();context.moveTo(curve[0][0], curve[0][1]);for (var i = 1; i < curve.length; i++) {context.lineTo(curve[i][0], curve[i][1]);}context.lineCap = "round";context.stroke();
}function isFlat(curve) {// var tol = 100000; // this is the max tol// var tol = 100; // barely wobblyvar tol = 10;var ax = 3.0*curve[1][0] - 2.0*curve[0][0] - curve[3][0]; ax *= ax;var ay = 3.0*curve[1][1] - 2.0*curve[0][1] - curve[3][1]; ay *= ay;var bx = 3.0*curve[2][0] - curve[0][0] - 2.0*curve[3][0]; bx *= bx;var by = 3.0*curve[2][1] - curve[0][1] - 2.0*curve[3][1]; by *= by;return (Math.max(ax, bx) + Math.max(ay, by) <= tol);
}function drawCurve(curve, context) {if (isFlat(curve)) {drawSegments(curve, context);} else {var pieces = subdivide(curve);drawCurve(pieces[0], context);drawCurve(pieces[1], context);}
}function paintDrawing(drawing) {for (var i = 0; i < drawing.curves.length; i++) {drawCurve(drawing.curves[i], drawing.context);}
}

我们准备好


function initContextAttrs(context) {context.strokeStyle = "#000000";context.lineWidth = 3;
}function init() {var context = document.getElementById("canvas").getContext("2d");initContextAttrs(context);curve = new Object();curve.context = context;curve.numCurves = 8;curve.curves = [[[180,280], [183,268], [186,256], [189,244]], // front leg[[191,244], [290,244], [300,230], [339,245]], // tummy[[340,246], [350,290], [360,300], [355,210]], // back leg[[353,210], [370,207], [380,196], [375,193]], // tail[[375,193], [310,220], [190,220], [164,205]], // back[[164,205], [135,194], [135,265], [153,275]], // ear start[[153,275], [168,275], [170,180], [150,190]], // ear end + head[[149,190], [122,214], [142,204], [85,240]],  // nose bridge[[86,240], [100,247], [125,233], [140,238]]   // mouth];paintDrawing(curve);var tangle = new Tangle(document, {initialize: function () { var front = curve.curves[0];var tummy = curve.curves[1];var backleg = curve.curves[2];var tail = curve.curves[3];var back = curve.curves[4];var earstart = curve.curves[5];var earfinish = curve.curves[6];var nose = curve.curves[7];var mouth = curve.curves[8];this.front0x = front[0][0]; this.front0y = front[0][1]; this.front1x =
front[1][0]; this.front1y = front[1][1]; this.front2x = front[2][0];
this.front2y = front[2][1]; this.front3x = front[3][0]; this.front3y =
front[3][1]; this.tummy0x = tummy[0][0]; this.tummy0y = tummy[0][1];
this.tummy1x = tummy[1][0]; this.tummy1y = tummy[1][1]; this.tummy2x =
tummy[2][0]; this.tummy2y = tummy[2][1]; this.tummy3x = tummy[3][0];
this.tummy3y = tummy[3][1]; this.backleg0x = backleg[0][0]; this.backleg0y =
backleg[0][1]; this.backleg1x = backleg[1][0]; this.backleg1y = backleg[1][1];
this.backleg2x = backleg[2][0]; this.backleg2y = backleg[2][1]; this.backleg3x
= backleg[3][0]; this.backleg3y = backleg[3][1]; this.tail0x = tail[0][0];
this.tail0y = tail[0][1]; this.tail1x = tail[1][0]; this.tail1y = tail[1][1];
this.tail2x = tail[2][0]; this.tail2y = tail[2][1]; this.tail3x = tail[3][0];
this.tail3y = tail[3][1]; this.back0x = back[0][0]; this.back0y = back[0][1];
this.back1x = back[1][0]; this.back1y = back[1][1]; this.back2x = back[2][0];
this.back2y = back[2][1]; this.back3x = back[3][0]; this.back3y = back[3][1];
this.earstart0x = earstart[0][0]; this.earstart0y = earstart[0][1];
this.earstart1x = earstart[1][0]; this.earstart1y = earstart[1][1];
this.earstart2x = earstart[2][0]; this.earstart2y = earstart[2][1];
this.earstart3x = earstart[3][0]; this.earstart3y = earstart[3][1];
this.earfinish0x = earfinish[0][0]; this.earfinish0y = earfinish[0][1];
this.earfinish1x = earfinish[1][0]; this.earfinish1y = earfinish[1][1];
this.earfinish2x = earfinish[2][0]; this.earfinish2y = earfinish[2][1];
this.earfinish3x = earfinish[3][0]; this.earfinish3y = earfinish[3][1];
this.nose0x = nose[0][0]; this.nose0y = nose[0][1]; this.nose1x = nose[1][0];
this.nose1y = nose[1][1]; this.nose2x = nose[2][0]; this.nose2y = nose[2][1];
this.nose3x = nose[3][0]; this.nose3y = nose[3][1]; this.mouth0x = mouth[0][0];
this.mouth0y = mouth[0][1]; this.mouth1x = mouth[1][0]; this.mouth1y =
mouth[1][1]; this.mouth2x = mouth[2][0]; this.mouth2y = mouth[2][1];
this.mouth3x = mouth[3][0]; this.mouth3y = mouth[3][1]; },update:     function () { var front = curve.curves[0];var tummy = curve.curves[1];var backleg = curve.curves[2];var tail = curve.curves[3];var back = curve.curves[4];var earstart = curve.curves[5];var earfinish = curve.curves[6];var nose = curve.curves[7];var mouth = curve.curves[8];front[0][0] = this.front0x ; front[0][1] =  this.front0y ; front[1][0] =
this.front1x ; front[1][1] =  this.front1y ; front[2][0] =  this.front2x ;
front[2][1] =  this.front2y ; front[3][0] =  this.front3x ; front[3][1] =
this.front3y ; tummy[0][0] =  this.tummy0x ; tummy[0][1] =  this.tummy0y ;
tummy[1][0] =  this.tummy1x ; tummy[1][1] =  this.tummy1y ; tummy[2][0] =
this.tummy2x ; tummy[2][1] =  this.tummy2y ; tummy[3][0] =  this.tummy3x ;
tummy[3][1] =  this.tummy3y ; backleg[0][0] =  this.backleg0x ; backleg[0][1] =
this.backleg0y ; backleg[1][0] =  this.backleg1x ; backleg[1][1] =
this.backleg1y ; backleg[2][0] =  this.backleg2x ; backleg[2][1] =
this.backleg2y ; backleg[3][0] =  this.backleg3x ; backleg[3][1] =
this.backleg3y ; tail[0][0] =  this.tail0x ; tail[0][1] =  this.tail0y ;
tail[1][0] =  this.tail1x ; tail[1][1] =  this.tail1y ; tail[2][0] =
this.tail2x ; tail[2][1] =  this.tail2y ; tail[3][0] =  this.tail3x ;
tail[3][1] =  this.tail3y ; back[0][0] =  this.back0x ; back[0][1] =
this.back0y ; back[1][0] =  this.back1x ; back[1][1] =  this.back1y ;
back[2][0] =  this.back2x ; back[2][1] =  this.back2y ; back[3][0] =
this.back3x ; back[3][1] =  this.back3y ; earstart[0][0] =  this.earstart0x ;
earstart[0][1] =  this.earstart0y ; earstart[1][0] =  this.earstart1x ;
earstart[1][1] =  this.earstart1y ; earstart[2][0] =  this.earstart2x ;
earstart[2][1] =  this.earstart2y ; earstart[3][0] =  this.earstart3x ;
earstart[3][1] =  this.earstart3y ; earfinish[0][0] =  this.earfinish0x ;
earfinish[0][1] =  this.earfinish0y ; earfinish[1][0] =  this.earfinish1x ;
earfinish[1][1] =  this.earfinish1y ; earfinish[2][0] =  this.earfinish2x ;
earfinish[2][1] =  this.earfinish2y ; earfinish[3][0] =  this.earfinish3x ;
earfinish[3][1] =  this.earfinish3y ; nose[0][0] =  this.nose0x ; nose[0][1] =
this.nose0y ; nose[1][0] =  this.nose1x ; nose[1][1] =  this.nose1y ;
nose[2][0] =  this.nose2x ; nose[2][1] =  this.nose2y ; nose[3][0] =
this.nose3x ; nose[3][1] =  this.nose3y ; mouth[0][0] =  this.mouth0x ;
mouth[0][1] =  this.mouth0y ; mouth[1][0] =  this.mouth1x ; mouth[1][1] =
this.mouth1y ; mouth[2][0] =  this.mouth2x ; mouth[2][1] =  this.mouth2y ;
mouth[3][0] =  this.mouth3x ; mouth[3][1] =  this.mouth3y ;context.clearRect(0,0, context.canvas.width, context.canvas.height);paintDrawing(curve);}});}

就这样，我们完成了。根据毕加索的《狗》画作，用九条贝塞尔曲线序列绘制，是不是很相似？