pytorch基本运算-分离计算

【1】引言

前序学习进程中，已经对pytor求导有了基本认识，知道requires_grad_(True)和backward()是求导必备的声明。
但有一种特殊情况，如果变量$z=f(xy)$，但同时$y=f(x)$，也就是变量$y$是变量$x$的函数，变量$z$同时是变量$y$和变量$x$的函数，此时可以有表达式：
$$z=f(xy)=f(x(f(x)))$$如果我们就是想获得$y$计算出来后，$z$关于$x$的导数，，此时就要考虑如何将$y$单独分流出来，不要让梯度经过$y$追溯到$x$。
这就是本次要学习的重点：分离计算。

【2】detach()函数

分离计算要使用detach()函数，用一个自定义的新变量名比如$t$来获取原变量$y$的值，此时把$z$的表达式改写成：
$$z=f(xy)=f(xt))$$
此时计算$\frac{dz}{dc}$就不会通过$t$传递到$x$，$t$只是一个和$y$相等的常数。
为此找一个例子做测试。

# 引入模块
import torch
from torch.autograd import backward# 定义初始张量
x=torch.arange(5.0)
# 声明要对x求导
z=x.requires_grad_(True)
print('z=',z)
# 乘积定义
y=x*x
z=y*x
# 梯度计算
z.sum().backward()
print('z=',z)
# 此时没有单独提取y
g1=x.grad
print('g1=',g1)
# 梯度清零
x.grad.zero_()
# 使用t分离y
t=y.detach()
# 重新定义函数
z=t*x
# 计算梯度
z.sum().backward()
print('z=',z)
# g2是用t分离y后获得的梯度
g2=x.grad
print('g2=',g2)
# 理论上，根据z=t*x，如果t是一个常数，梯度结果就是t
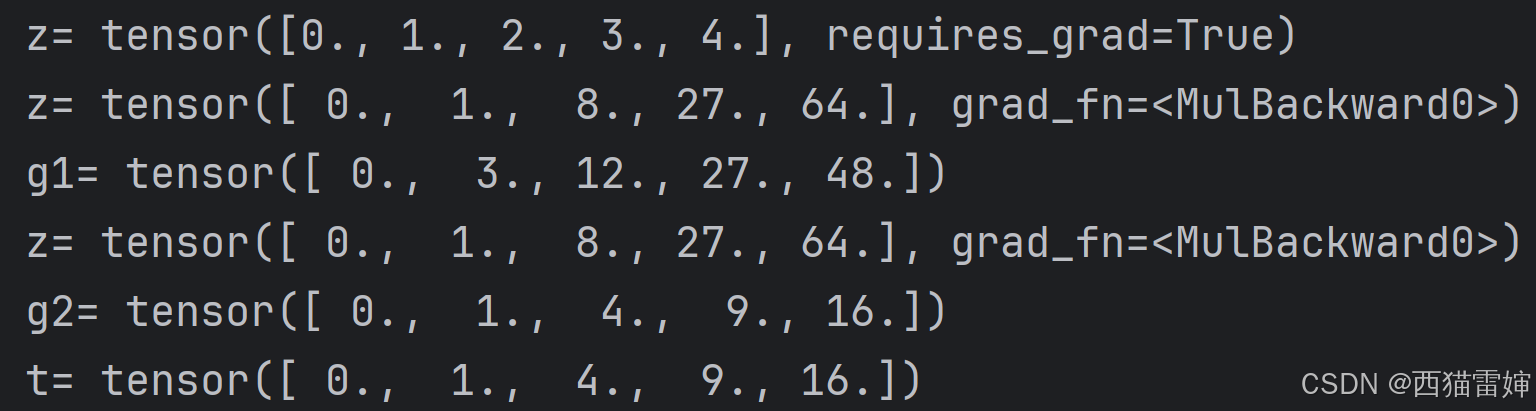
print('t=',t)

这个代码块先计算了不分离$y$的梯度$g1$，然后计算了分离$y$的梯度$g2$，证明了分离后确实梯度计算不会再由$t$追溯到$x$，实现了保持$y$为常数的运算目标。
计算结果为：

【3】总结

学习了pytorch分离计算导数的基本概念。