数组常见算法

一、查找算法

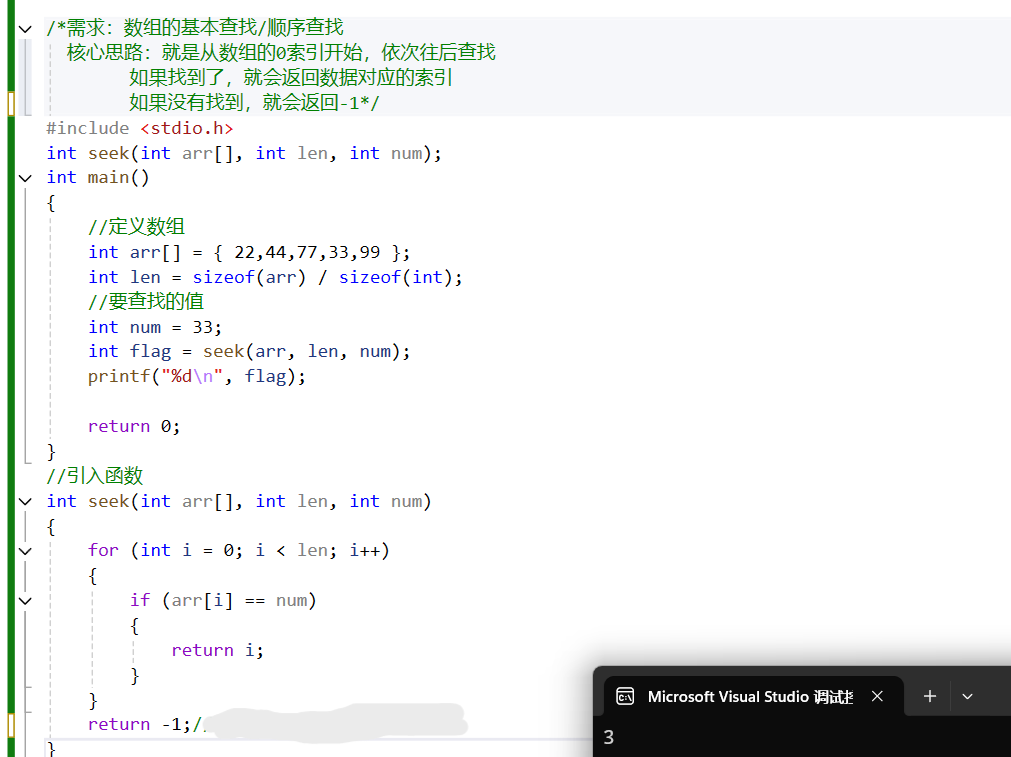
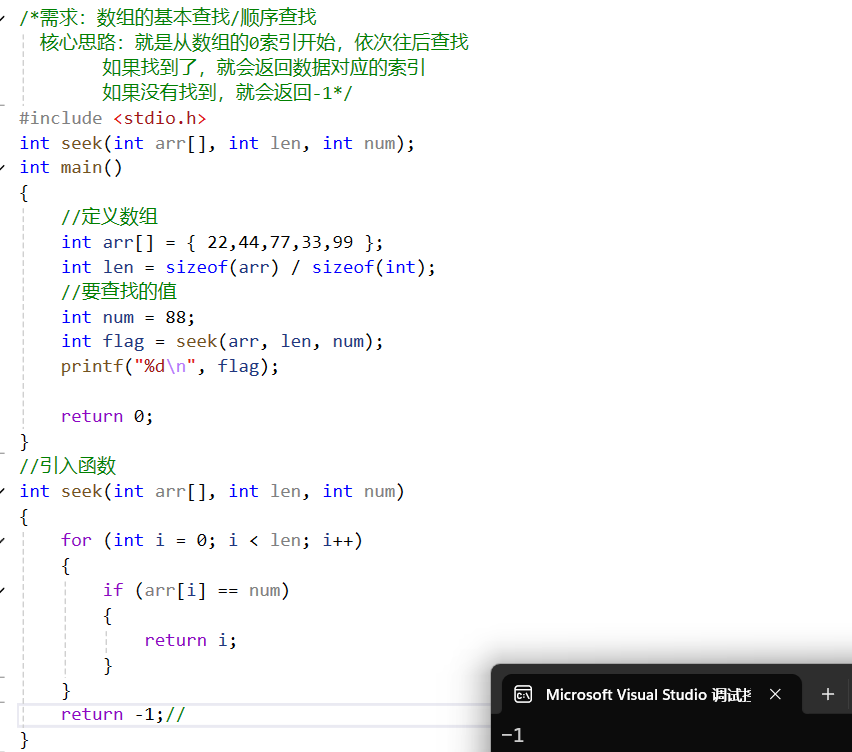
1.基本查找（/顺序查找）

对数据没有任何要求，从头到尾遍历数组即可

2.二分查找

• 前提条件：数组中的数据必须是有序的，不论是从大到小还是从小到大
• 核心逻辑：每次排除一半的查找范围
• 实质：缩小查找范围

1. min和max表示当前要查找的范围
2. mid是在min和max中间的
3. 如果要查找的元素在mid左边，缩小范围时，min不变，max等于mid减1
4. 如果要查找的元素在mid右边，缩小范围时，max不变，min等于mid加1

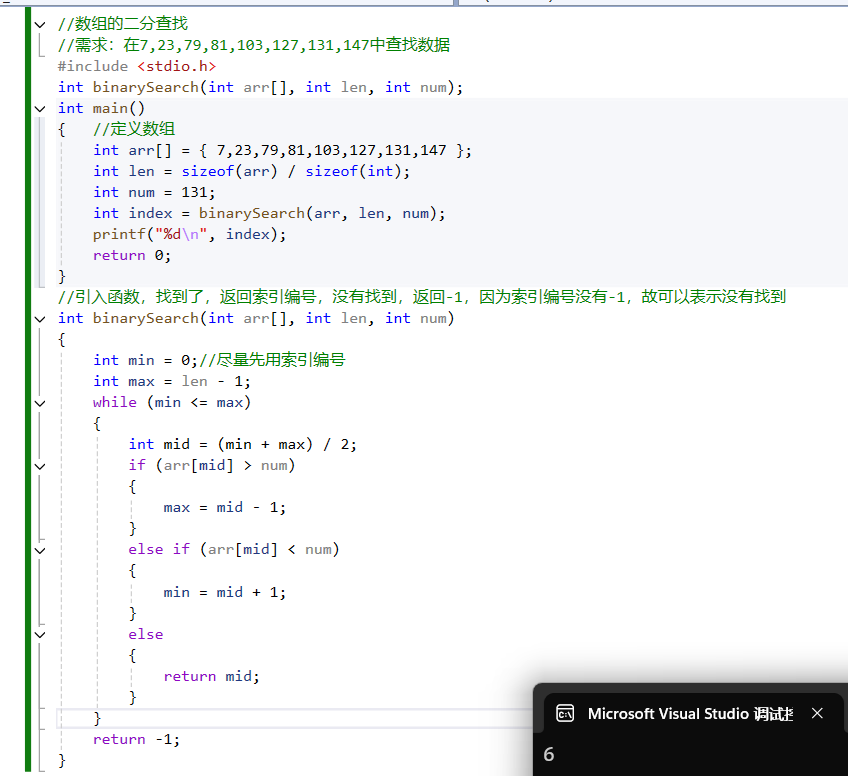
此处mid定义要写在while里面，这样每次开始时mid值才会发生改变, 因为mid的值是在max和min改变之后进行除2的

ps：如果数据是乱的，先排序在进行二分查找得到的索引没有实际意义，只能确定当前数字在数组中是否存在，因为排序之后数字的位置就可能发生变化了，那么得到的索引就不是原来乱序的索引了，就没有意义

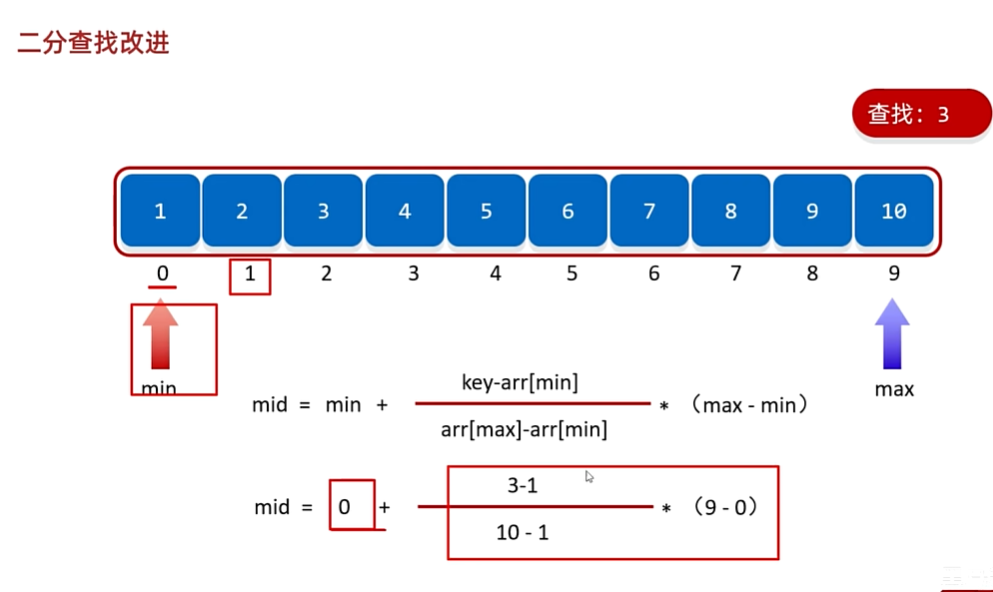
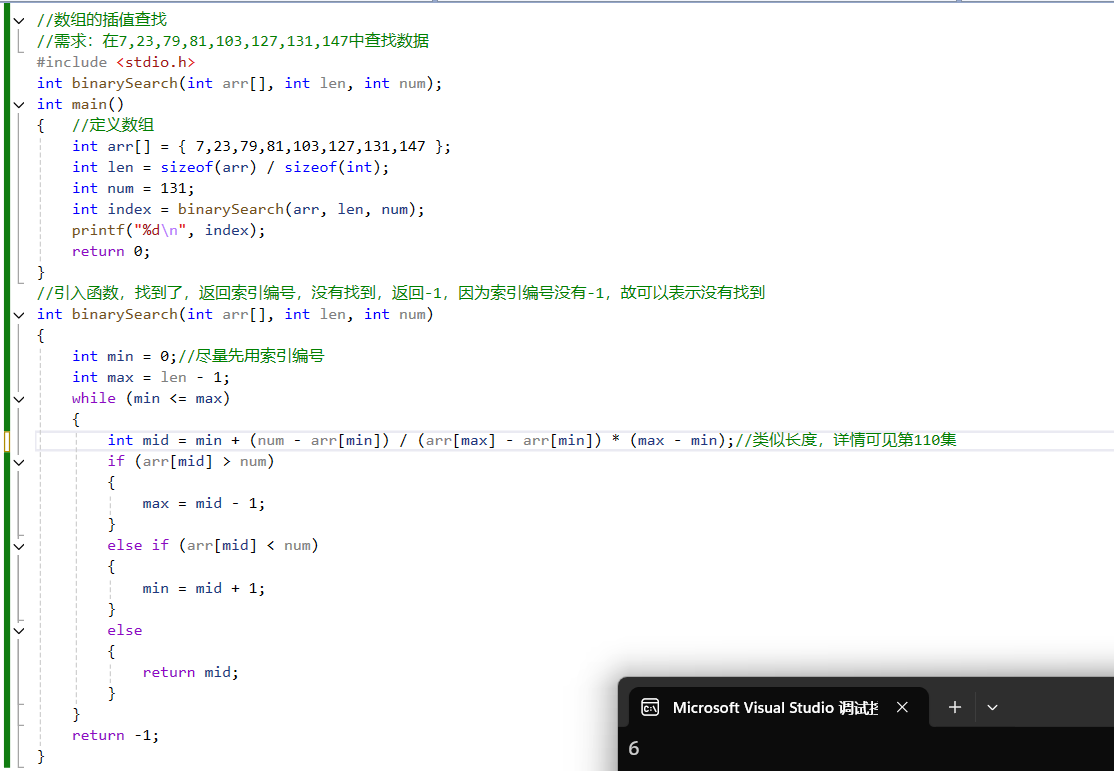
3.插值查找

减少二分查找的次数

• 要求：数据要有序，且数据分布尽可能的均匀一点，mid尽可能的靠近要查找的数据
• 优势：数据分布均匀，效率比二分查找快，否则反而会更慢

实际上只要修改mid值就可以了（详细可见第110集）

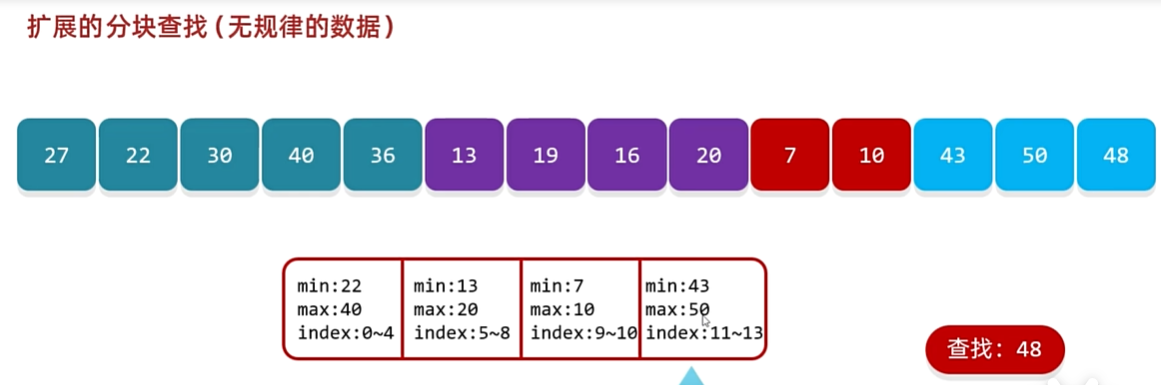
4.分块查找

• 核心思路：先确定要查找的元素在哪一块，然后在块内挨个查找
• 分块的原则1：前一块中的最大数据，小于后一块中所有的数据（块内无序，块间有序）
• 分块的原则2：块数数量一般等于数字的个数开根号。比如：16个数字一般分为4块左右，但如果数据分块不能和想要的一样，可以合理分块，例如：

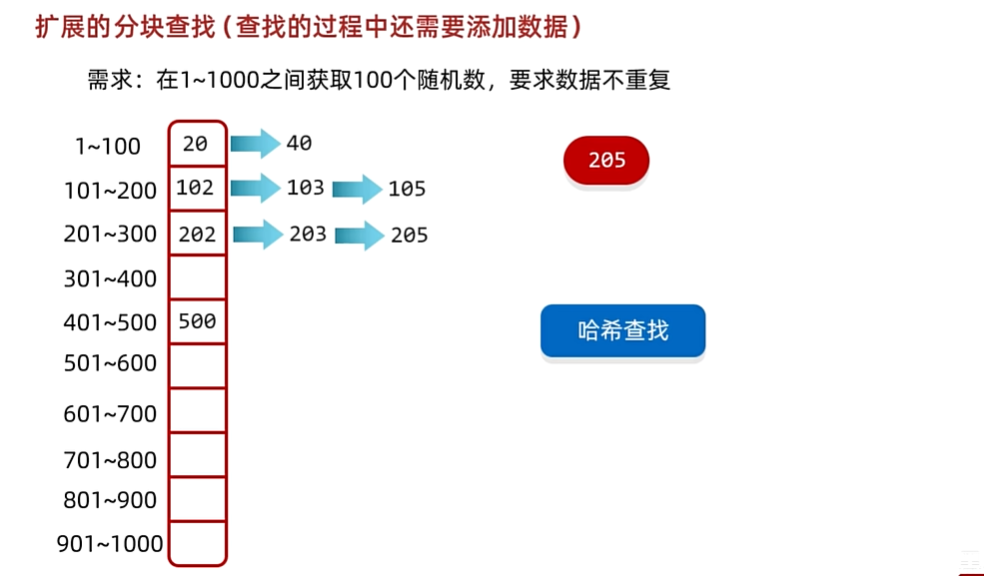
5.哈希查找

实质上就是在查找的过程中还要添加数据，是分块查找的扩展

在查找数据没有重复后再添加数据到数组中，但如果没有重复，可以先挂在这个范围内

6.树表查找

7.斐波那契查找

二、排序算法

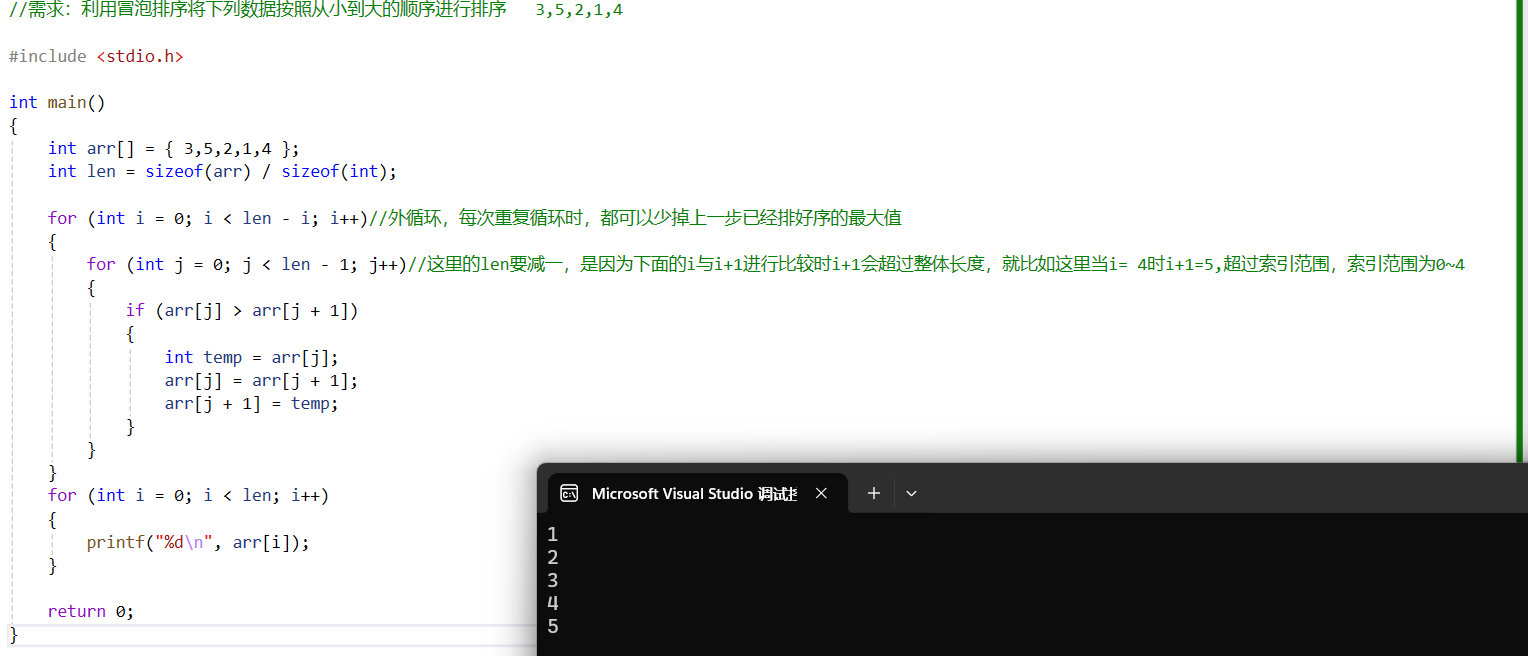
1.冒泡排序

• 核心思想：相邻的数据两两比较，小的放在前面，大的放在后面
• 第一轮循环结束，最大值已经找到，在数组的最右边，第二轮循环只要在剩下的元素找最大值就可以了，第二轮循环结束，次大值已经确定，第三轮就继续在剩下的数据中循环，以此类推，直到数据正常排序，在比较完第一轮去比较第二轮时，不用像第一轮一样从头比到尾，可以只比到倒数第二个，少比较一个，提高效率，后面以此类推
• 如果数组中有n个数据，总共我们只要执行n-1轮的代码就可以

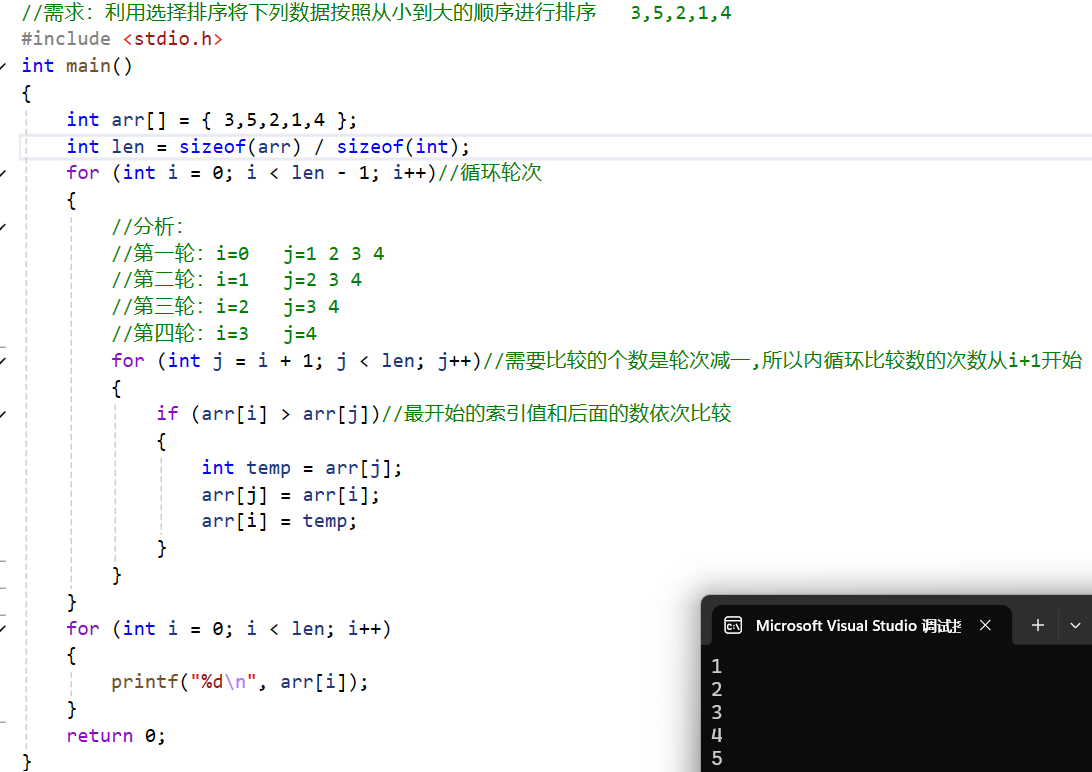
2.选择排序

• 核心思想：从0索引开始，拿着每一个索引上的元素跟后面的元素依次比较，小的放前面，大的放后面，以此类推，图例：

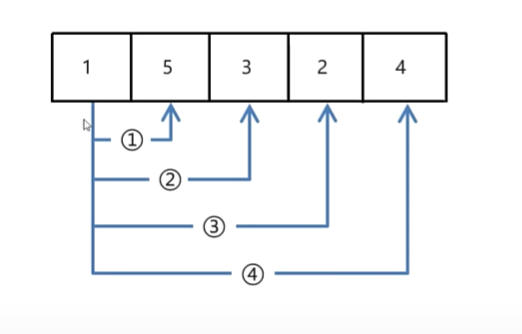
• 第一轮循环结束后，最小的数据已经确定，第二轮循环从1索引开始，以此类推