插入排序与希尔排序

笔者把源码放在github上了：Fundamentals-of-Data-Struct/Sort at main · z-yi-han/Fundamentals-of-Data-Struct

本文笔者带领读者进行排序的学习，今天我们学习插入排序与希尔排序。

首先，我们先介绍插入排序。读者可能不知道什么是插入排序，笔者给大家举个例子：打扑克牌的时候整理牌，其实这就是一种插入排序，所以我们不难理解插入排序：给定一个数组，取一个元素，在这个元素与其前面的元素一一对比，碰到大于他的就交换位置（这里是升序，降序就是小于)，依次从第一个元素开始每个都和前面比较即可，对应的下标是【0，n-1】。对于排序问题，不管是什么排序，我们都要先把一趟的代码写出来再总循环一次，下面我们就开始写插入排序一趟的代码：

首先，我们考虑范围，数组要用下标为参考，假设需要插入的元素下标是end+1，前面就是【0，end】，因此我们只需要一个一个对比，再判断即可：

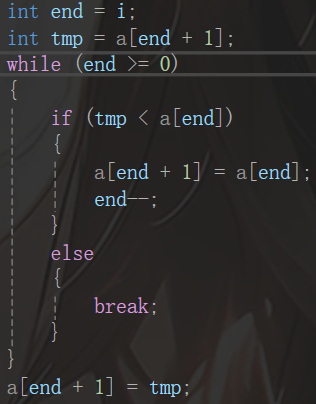
观察上面的代码，首先定义了end,i其实是方便整体循环，然后笔者把a[end+1]存起来了，这是因为这样这个位置对应的值可能改变，然后直接开始比即可，从后往前比，如果满足条件，那就把end往前动一个单位，如果不符合直接跳出，最后，这个最开始存的再让他回去就行，不过需要注意的是，这一步需要推出while循环在进行，这是为了方便，然后在套在循环里：

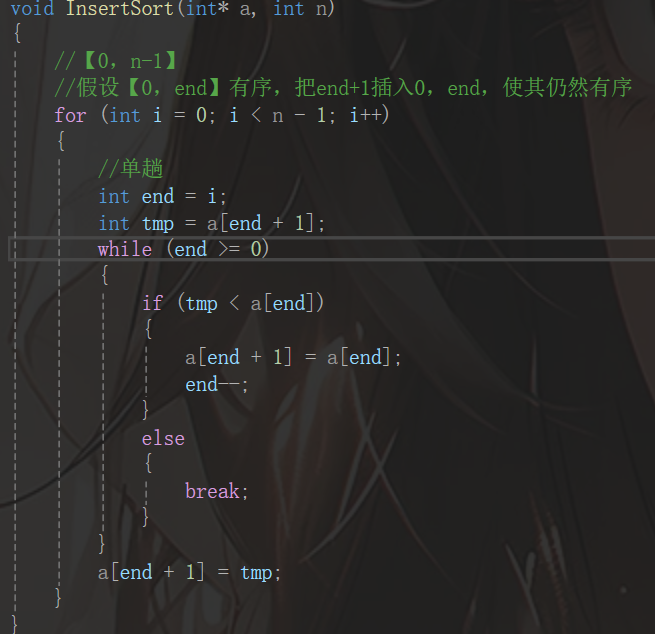
最后我们可以做个测试：

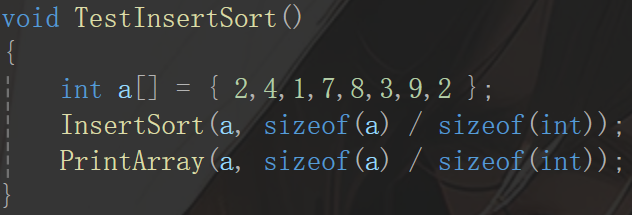
然后我们可以分析一下插入排序的时间复杂度：首先考虑最坏情况，假如说全部都是逆序，也就是说从最后一个就全部遍历，也就构成了一个等差数列，时间复杂度就是O(N^2),如果是最好情况，那么也就是O(N),因此这种排序的时间复杂度是O（N^2)。

下面，笔者介绍一种比较抽象的排序——希尔排序：

希尔排序其实也是插入排序，但是时间复杂度得到了很大的优化，这是由于希尔排序的特点——预排序+插入排序。首先，笔者先带领读者一步一步分析一下希尔排序：希尔排序法又称缩小增量法，预处理是为了让其更接近有序，也就是说在接近有序的基础上再进行排序会让插入排序的效率优化很多，因此我们先思考什么是预处理：其实就是先分组，选一个值gap,然后从第一个值开始分组，每间隔gap的元素为一个组，然后对这个组里的元素进行插入排序，需要注意的是，这里gap的选择理论上是都可行的，但是经过计算，gap取3是最合适的，当然gap取1的时候就是正常的快速排序，gap越大，跳的越快，越无序。下面给定一个数组：9 1 2 5 7 4 8 6  3 5

假如gap是3，那么一组就是9 5 8 5，笔者写一段代码对这段进行排序：

其实就是一个快速排序，但是这里笔者没有把i的范围写上，笔者希望读者和笔者一同思考这个范围是什么，我们都知道数组不能进行越界访问，因为i的范围就是为了防止越界访问，一共有n个元素，但是这组中两两间隔为gap，所以i必须<n-gap，因为如果i等于它，end+gap就会是n,造成越界，故代码如下图：

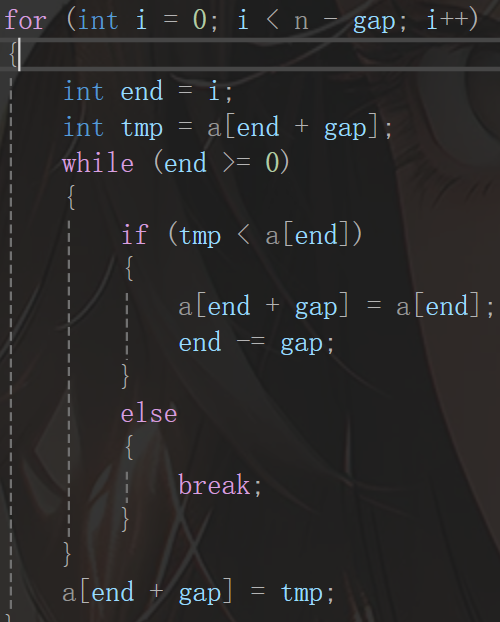
这是其中一组的，这组进行之后，排序还没结束，应该继续进行，所以这里需要一个while循环，不过这里需要注意的是gap的控制，gap取3会比较合适，这里用了一下Knuth 序列：gap = gap / 3 + 1：

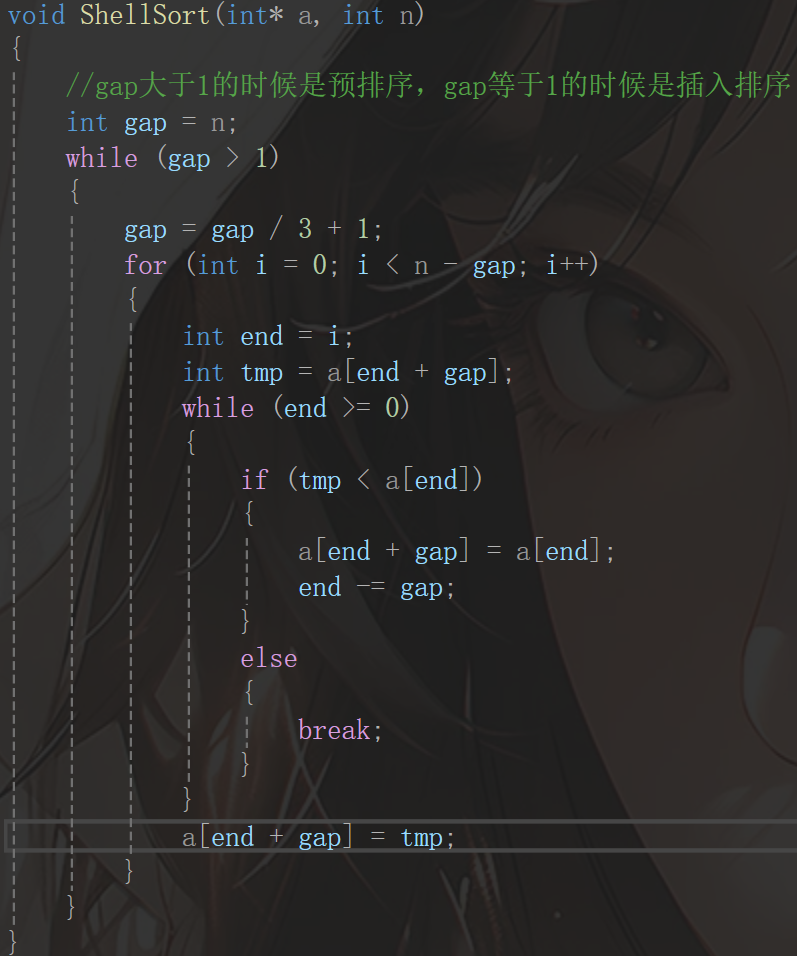
然后这种排序的时间复杂度比较麻烦，读者记住即可：O（N^1,3）,感兴趣的读者可自行查阅。

最后进行一个小测试：

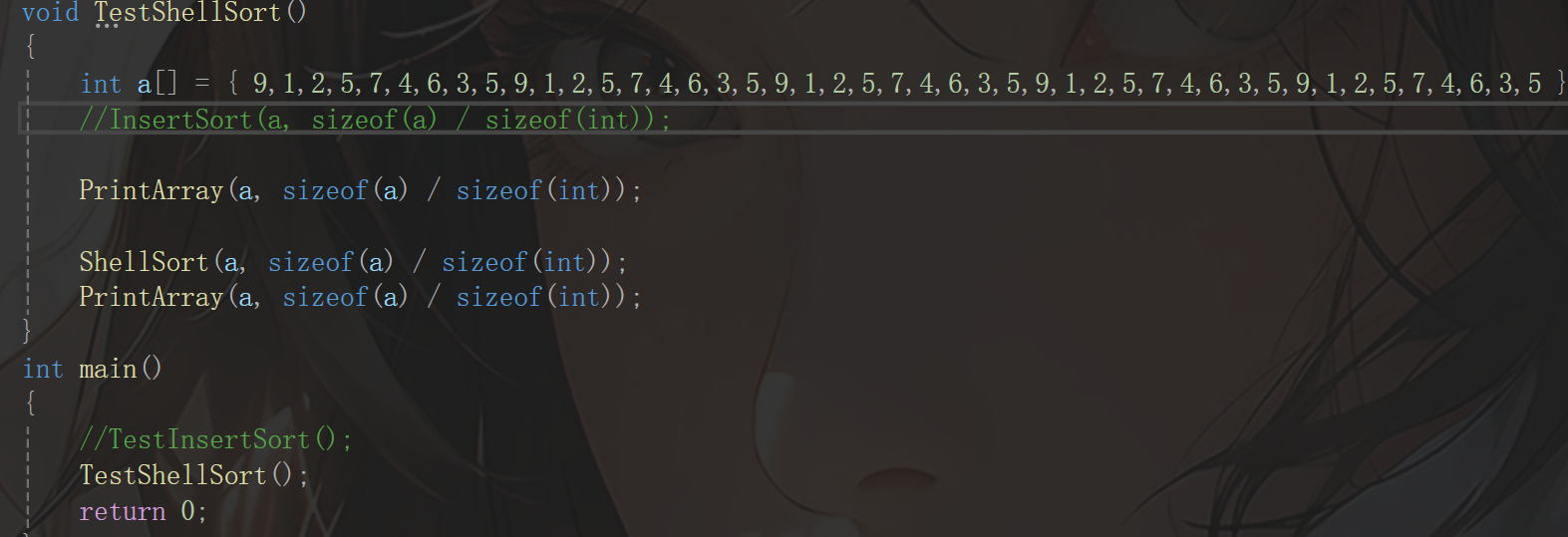
希望读者能给笔者点个赞。