状压 dp --- 数据范围小
hello,大家好,我们又见面了!今天是2025年9月6日,我们继续开启 状压 dp 的学习。
一:简介
状压 dp 常用于解决的第三种问题就是当数据范围很小但是暴搜的话会超时。
这类问题相对于前两类问题比较灵活,但是也是有明显的特征:属于 n 很小,但是暴搜的话即使加上优化和剪枝也会超时,因此,我们可以往状压 dp 的方向去思考。
接下来的两大题目都会讲到之前没有了解过的新东西,既然大家点进来了,就不要跳过了,我相信大家看完后一定会有所收获。
二:经典题目
题目一:糖果
题目链接:糖果
在这道题目中,会讲述一种之前我们很少用到的推导状态转移方程的方式,希望大家一定不要跳过
【题目描述】
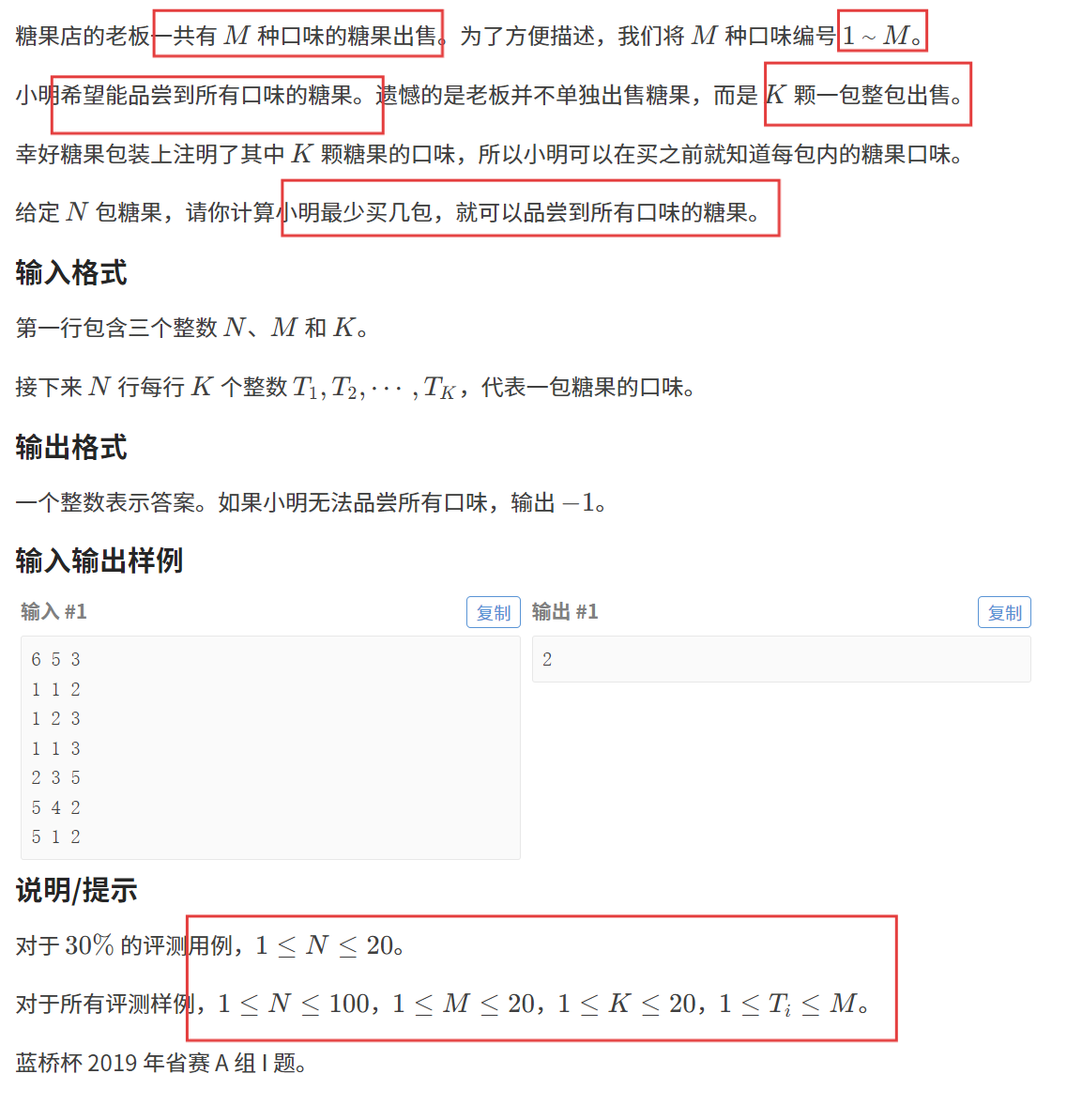
【算法原理】
解法一:状态压缩 + 最短路 + BFS(最优解)(这个解法前面已经讲过了,就不再赘述了)
解法二:状压 dp
对于这类数据范围很小的问题,我们首先应该想到的解法就是暴力搜索。但是这道题目暴搜策略不好想而且时间复杂度会非常高,因此我们考虑使用状压 dp 来解决这道问题。
1.状态表示:(经验 + 题目要求)
f[x]表示:凑成糖果的口味状态为 x 时,最少需要多少包糖果。

2.最终结果:
如果这样定义状态表示的话,根据题目要求,最终结果显然是 f[2 ^ m - 1];
3.状态转移方程:(考虑最近的一步来分析问题)
我们考虑最近的一步,看一看有哪些状态可以通过再购买一包糖果后更新到 x 上。
这样更新状态的话要保证 x 之前的状态全部已经计算出来了。但是我们发现,前面的状态并不好确定。对于一包糖果而言,可以找到很多前驱状态。
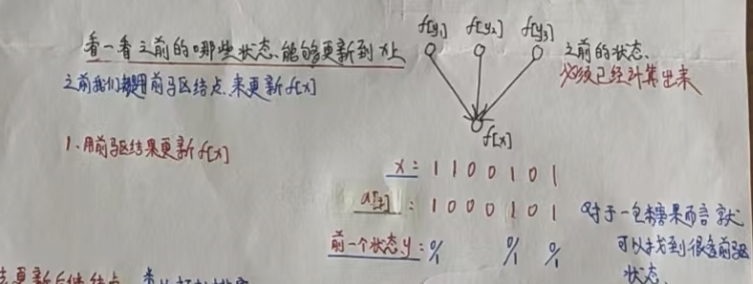
因此,我们换一种思维方式,使用 f[x] 去更新后继节点(类似于拓扑排序),这样的话,状态转移方程就很好推导了,直接将某一包的糖果状态按位或进去就行了。
f[x | a[i]] = min(f[x | a[i]],f[x] + 1);

4.初始化:
所有格子初始化为正无穷,f[0] = 0 即可。(最初的状态 0 去更新后面的状态)
5.填表顺序:
保证 f[x] 更新完毕之后然后才能去更新后继结点,因此我们只需保证从大到小枚举状态即可。
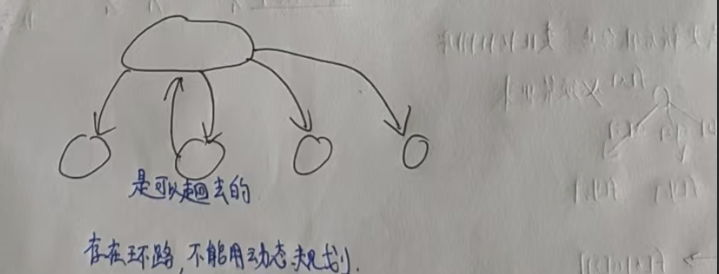
最后解释一个问题:为什么这道题可以使用状压 dp 而《关灯问题II》这道题目却不能使用呢?
因为本题状态是不会回退的,《关灯问题II》这道题目状态有可能回退,图中会出现环路,存在环路时不能使用动态规划的!!!
【代码实现】
#include <iostream>
#include <cstring>using namespace std;const int N = 110, M = 21;int n, m, k;
int a[N];int f[1 << M];int main()
{cin >> n >> m >> k;for(int i = 0; i < n; i++)for(int j = 0; j < k; j++){int x; cin >> x; x--;a[i] |= (1 << x);}memset(f, 0x3f, sizeof f);f[0] = 0;// s 一定要从 0 开始,因为我们要用 0 去更新后面的值 for(int s = 0; s < (1 << m); s++)for(int i = 0; i < n; i++)f[s | a[i]] = min(f[s | a[i]], f[s] + 1);if(f[(1 << m) - 1] == 0x3f3f3f3f) cout << -1 << endl;else cout << f[(1 << m) - 1] << endl; return 0;
}题目二:PRZ
题目链接:PRZ
【题目描述】
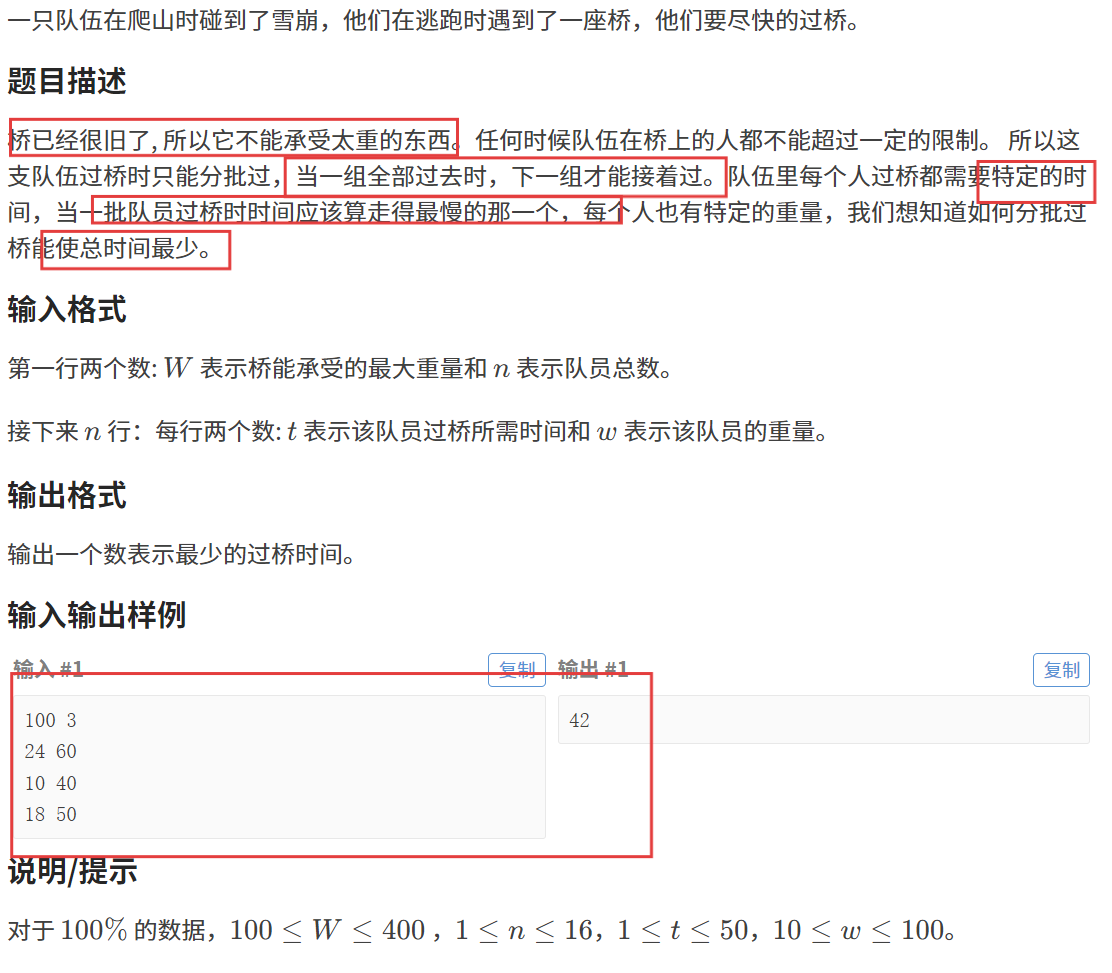
解释:一号和二号为一组,过桥时间为 24,三号自己一组,过桥时间为 18,所有人过桥的总时间最优为 24 + 18 = 42。
【前置知识】(很重要)
如何枚举一个状态的子状态:
类比我们之前学过的枚举子集:
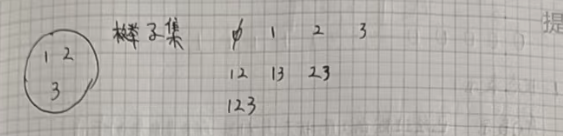
枚举一个状态的子状态:
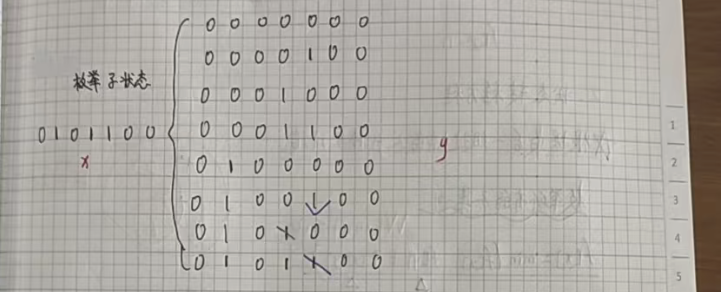
枚举方式:
for(int x = 0; x < (1 << n); x++)for(int y = x; ; y = x & (y - 1)){// y 就是 x 这个状态的一个子状态if(!y) break;}解释:



【算法原理】
本题数据范围很小,但是暴搜的话很难找到一种剪枝策略,因为这道题要考虑的因素比较多。
我们尝试使用 状压 dp 的方式来解决一下这道问题:
1.状态表示(经验 + 题目要求):
f[x] 表示:已经过桥人的状态为 x 时,所花费的最少时间。
2.最终结果:
根据状态表示以及题目要求,显然最终结果为 f[(1 << n) - 1]。
3.状态转移方程(根据最近的一步分情况讨论):
假设当前过桥状态 x 为 1,2,4,6,7 已过桥:
根据最后一组过桥的人分情况讨论:
我们枚举他们这些人中所有的子集 y:
当W[x ^ y] <= w 时(保证剩下的那些人能一次过桥),f[x] = min(f[x],f[y] + T[x ^ y]);

4.初始化:
因为我们要求的是最小值,因此所有格子的值先初始化为正无穷,f[0] = 0;
5.填表顺序:
枚举子集就可以了~~~。
【代码实现】
#include <iostream>
#include <cstring>using namespace std;const int N = 18;int m, n;
int t[N], w[N];int T[1 << N], W[1 << N], f[1 << N];int main()
{cin >> m >> n;for(int i = 0; i < n; i++) cin >> t[i] >> w[i];// 预处理出每一个状态的最大时间和总重for(int s = 0; s < (1 << n); s++)for(int i = 0; i < n; i++){if((s >> i) & 1){T[s] = max(T[s], t[i]);W[s] += w[i];}} memset(f, 0x3f, sizeof f);f[0] = 0;for(int x = 0; x < (1 << n); x++)for(int y = x; ; y = x & (y - 1)){if(W[x ^ y] <= m) f[x] = min(f[x], f[y] + T[x ^ y]);if(!y) break;}cout << f[(1 << n) - 1] << endl;return 0;
}好的,今天的分享就先到这里了,大家再见。
