线代：排列与逆序

1. 排列

n级排列：由1，2，3，...，n组成的一个有序数组

1，2，3，...，n的排列一共有n！个排列（n！为n的阶乘）

123...n按顺序排列，我们称为n级标准（自然）排列

如：123，321，312是3级排列，

12346则不是排列，因为其不是一个有序数组

2. 逆序

12453，这是一个5级排列，其中4,3和5,3为两个逆序，我们称这组排列中逆序数是2

逆序数的定义就是逆序的总数，记作N（i1i2,...,in）

        练习：

1.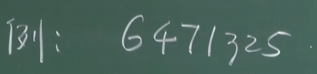有几个逆序数

解：

第一步：这个数本身减1

第二步：观察这个数前面有几个比它小的数，再减去比他小的数字的个数

第一位是6，那么6-1=5，前面没有比6小的数，5-0=5

第二位是4，那么4-1=3，前面没有比4小的数，3-0=3

第三位是7，那么7-1=6，前面有6、4两个数比7小，6-2=4

以此类推

得到结果：N(6471325)=13

2.有几个逆序数

解：

该排列为标准排列，故：

0个

3.有几个逆序数

解：

由该等差数列可知，其逆序数为(n-1)+(n-2)+...+2+1

根据等差数列求和公式【（首项+末项）*项数/2】得到 [(n-1)+1] * (n-1) / 2 = n(n-1)/2

n(n-1)/2个

3. 奇排列与偶排列

当排列中逆序数为奇数的时候，该排列被称为奇排列

当排序中逆序数为偶数的时候，该排列被成为偶排列

那么，

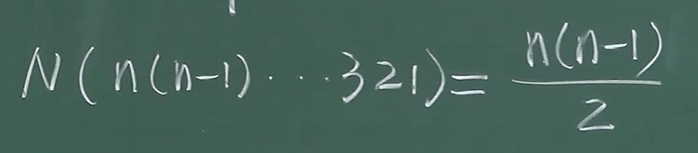
什么时候为奇排列，什么时候是偶排列呢？

我们不妨把从1到8带入n中，并计算每个排列的逆序数，计算后我们发现：

从结果我们不难发现，把每四个数字分成一组(4k)，

n= (4k+1)【第一项】和 (4k)【最后一项】是偶排列，

n= (4k+2)【第二项】和 (4k+3)【第三项】是奇排列

4. 对换

我们将一个排列中的两个数字对换，会发现其的逆序数发生了改变

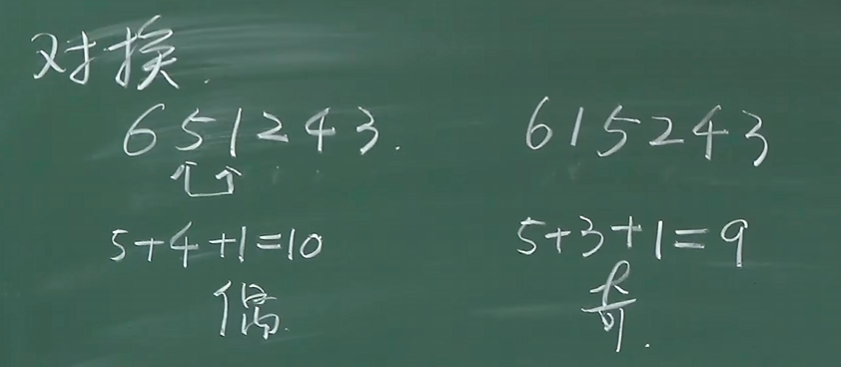
由此我们可知，对一个排列进行一次对换，其奇偶性会发生改变

那么如何证明呢？

假设一个数列a1-an,其中有两个任意数ai和ai+1,将其对换位置

由于此时我们不知道谁大谁小，我们就需要假设两种情况:

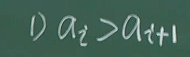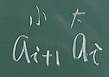，，我们会发现ai+1的逆序数没有变，但ai到ai+1的逆序由于对换了位置而没有了，此时整个排列的逆序数少了1，发生了奇偶性的变化。

同理，此时整个排列的逆序数多了1，发生了奇偶性的变化。

我们现在回到n阶排列，n阶排列共有n!个，那么在n!个中，有多少个奇排列，多少个偶排列呢？

首先，我们需要排除n=1的情况，因为{1}的逆序数是0，所以是偶排列，但排列极少会出现只有一个数的情况，所以我们排除这个极端情况。

那么，在n>=2的情况下，我们假设有p个奇排列，q个偶排列，如果我们对p中的一个奇排列进行对换，那么这个奇排列就会变成偶排列。那么，我们对p个奇排列全部都做对换，那么每一个奇排列都会一一对应一个偶排列，此时偶排列的个数就是q=(q+p)，所以q>=p。

同理q做对换，我们会得到p=(p+q)，所以p>=q。

因为此时需要同时满足条件p>=q和q>=p，所以p=q。

由此，我们得到：当 n≥2 时，偶排列和奇排列的数量严格相等，个数分别为 n!/2。