数据结构与算法1 第一章 绪论
课程视频来源:【《数据结构C语言版》3小时期末速成/数据结构与算法/各版本都可以用/严蔚敏版可用】 https://www.bilibili.com/video/BV1yEPLeDEZS/?share_source=copy_web&vd_source=2c56c6a2645587b49d62e5b12b253dca
入门视频一定是及格线包过,如果要高分,需要在章节前加上408搜索进阶课程,比如408线性表。
如果是代码实战视频,请关注我高中的信竞老师,她讲得很好:ilmnouvwx的个人空间-ilmnouvwx个人主页-哔哩哔哩视频
1 数据结构的基本术语
1.1 数据结构的基本术语
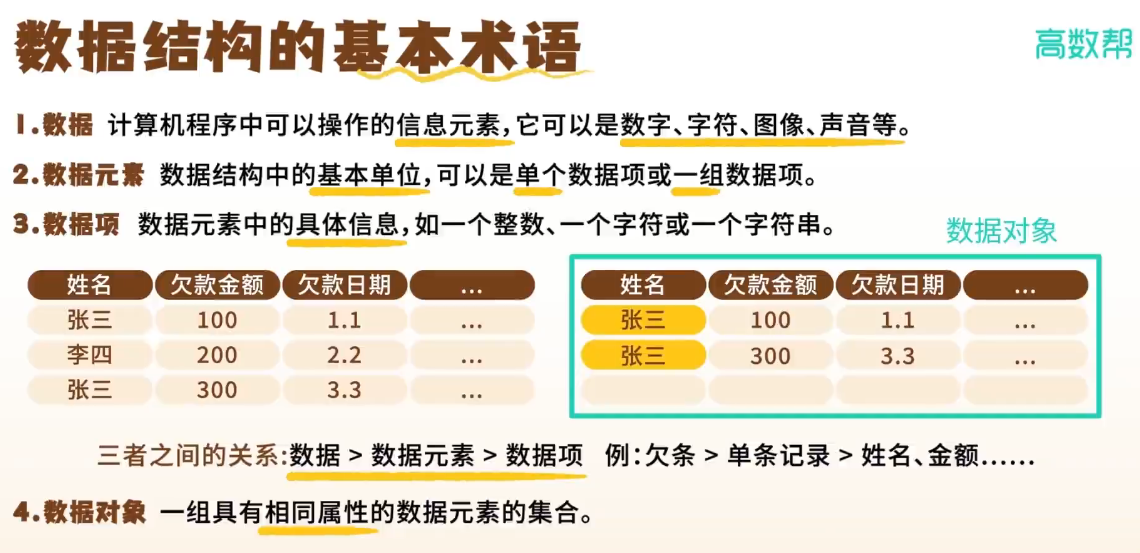
整个表格就是数据,每一行就是数据元素,每一格就是数据项。
将具有相同属性的数据元素放在一起就构成数据对象。
1.2 数据结构的分类
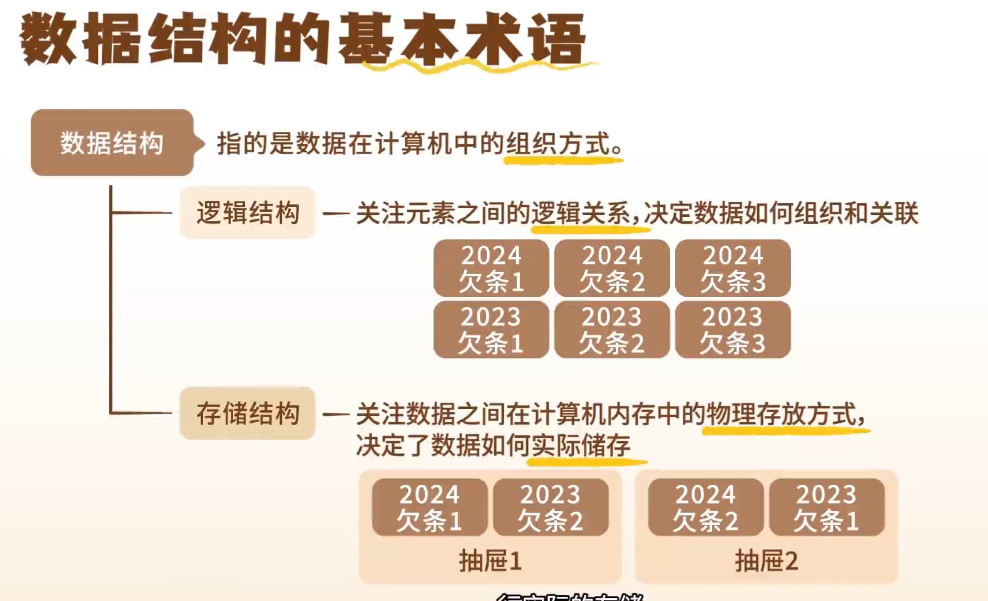
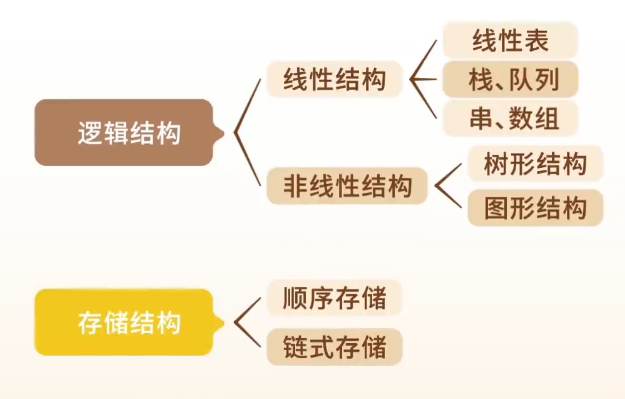
逻辑结构——关注元素之间的关系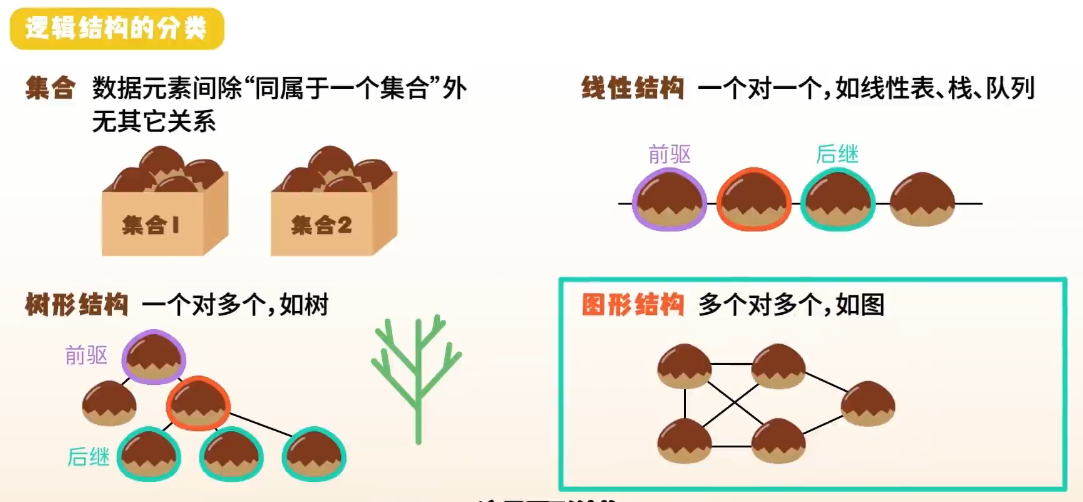
存储结构——如何存储,存哪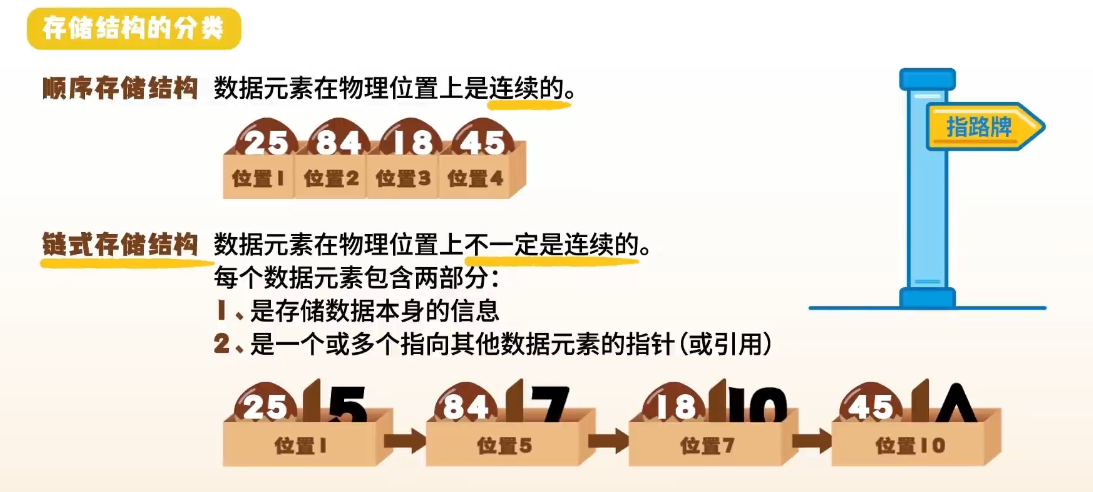
2 算法
2.1 算法五个特征

2.2 算法的评价

主要从高效性来评价:包括时间代价和空间代价
3 时间复杂度计算
【两种套路搞定所有时间复杂度408真题】 https://www.bilibili.com/video/BV1M1421R7nX/?share_source=copy_web&vd_source=2c56c6a2645587b49d62e5b12b253dca
思路:
遇到while考虑设t法
遇到递归考虑设t法
遇到非++--for考虑设t法
遇到for嵌套考虑①找关键语句 ②求和 ③计算(一般枚举后用数列求和解)
原理:探求t次和条件变量之间的关系什么时候满足,解出t
技巧:一般出现x=x*2这种语句都含有log2n的复杂度。(设t法检验)
邪修:特值代入/逼近排除法
Q:遇到while考虑设t法

Q:遇到for嵌套考虑①找关键语句 ②求和 ③计算(一般枚举后用数列求和解)

Q:遇到while考虑设t法

Q:遇到非++--for考虑设t法

Q:遇到递归考虑设t法

Q:内外不关联,乘起来就好

Q:遇到while考虑设t法 探求t次和条件变量(sum)之间的关系什么时候满足,解出t


到第t次跳出,此时x=t,满足跳出条件是(x+1)^2>n,满足时t=x,得到(t+1)^2>n,解出t
Q:内外侧关联,邪修逼近排除法

4 空间复杂度的计算
注意:数组传入时,大小是指针大小,在64位系统(寄存器最大处理数)下是8B

一般只有递归/创建线性表才会开辟新的辅助空间,只有参数的情况下无论for几次都没有开空间,因此大小都是O(1)。
考虑一个有趣的问题:如果每层递归都会创建一个n大小的数组是不是空间复杂度是n^2?
假设你有一个递归函数,递归深度为 n,每层都创建一个大小为 n 的数组:
def recursive_with_array(n):if n <= 0:returnarr = [0] * n # 每层都创建一个长度为 n 的数组print(f"Layer {n}, array size {len(arr)}")recursive_with_array(n - 1) # 递归调用📌 递归过程(以 n=3 为例):
recursive_with_array(3)
→ 创建arr3(大小 3)
→ 调用recursive_with_array(2)recursive_with_array(2)
→ 创建arr2(大小 2)
→ 调用recursive_with_array(1)recursive_with_array(1)
→ 创建arr1(大小 1)
→ 调用recursive_with_array(0)recursive_with_array(0)
→ 返回- 回到
recursive_with_array(1),函数结束,arr1被释放 - 回到
recursive_with_array(2),函数结束,arr2被释放 - 回到
recursive_with_array(3),函数结束,arr3被释放
⚠️ 关键点:这些数组是逐层创建、逐层释放的,不会同时存在。
- 在任意时刻,最多只有一层的数组在内存中(加上当前调用栈的其他局部变量)。
- 所以同时存在的最大额外空间是某一层的
O(n)数组 + 递归栈深度O(n)。 - 但
O(n)+O(n)=O(n),不是O(n²)!

