2、数学与经济管理

最小生成树
解法
目标:将n个节点联通,但是不能产生环路,保证成本最少
解法:依次用最小的成本连线,最后保证链接所有节点,并且没有回路。
1、视频
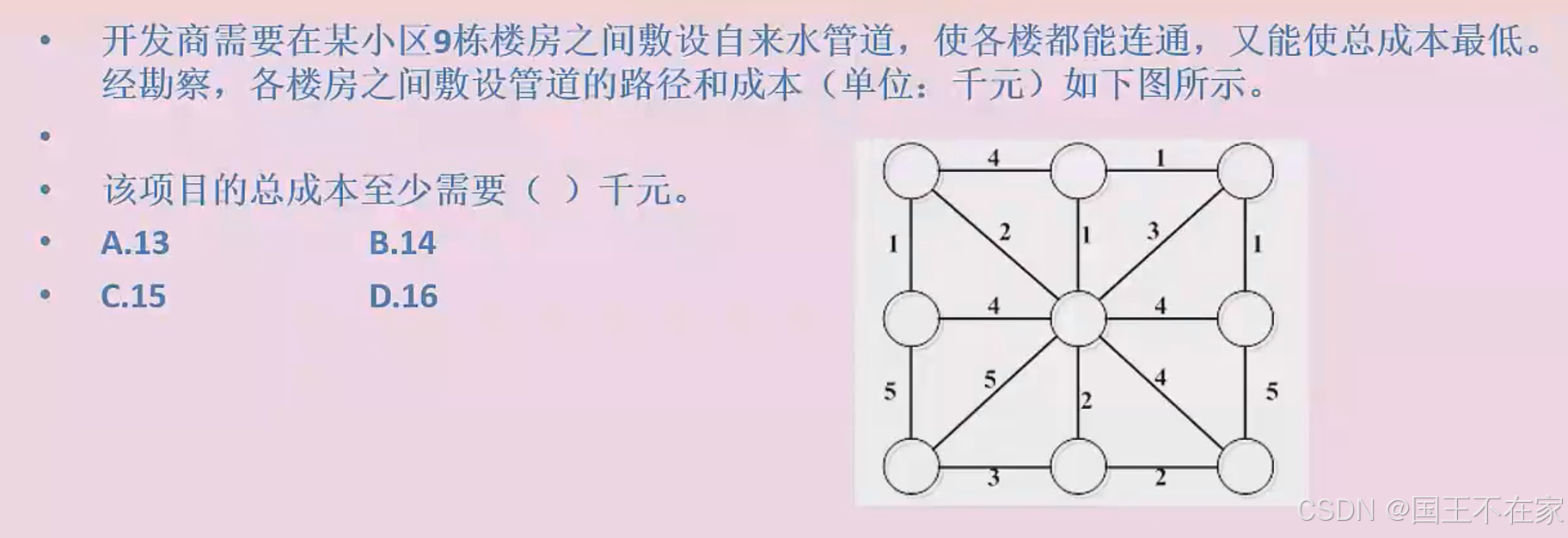
答案:A 13 = 4*1 +2*3 +3
2、视频
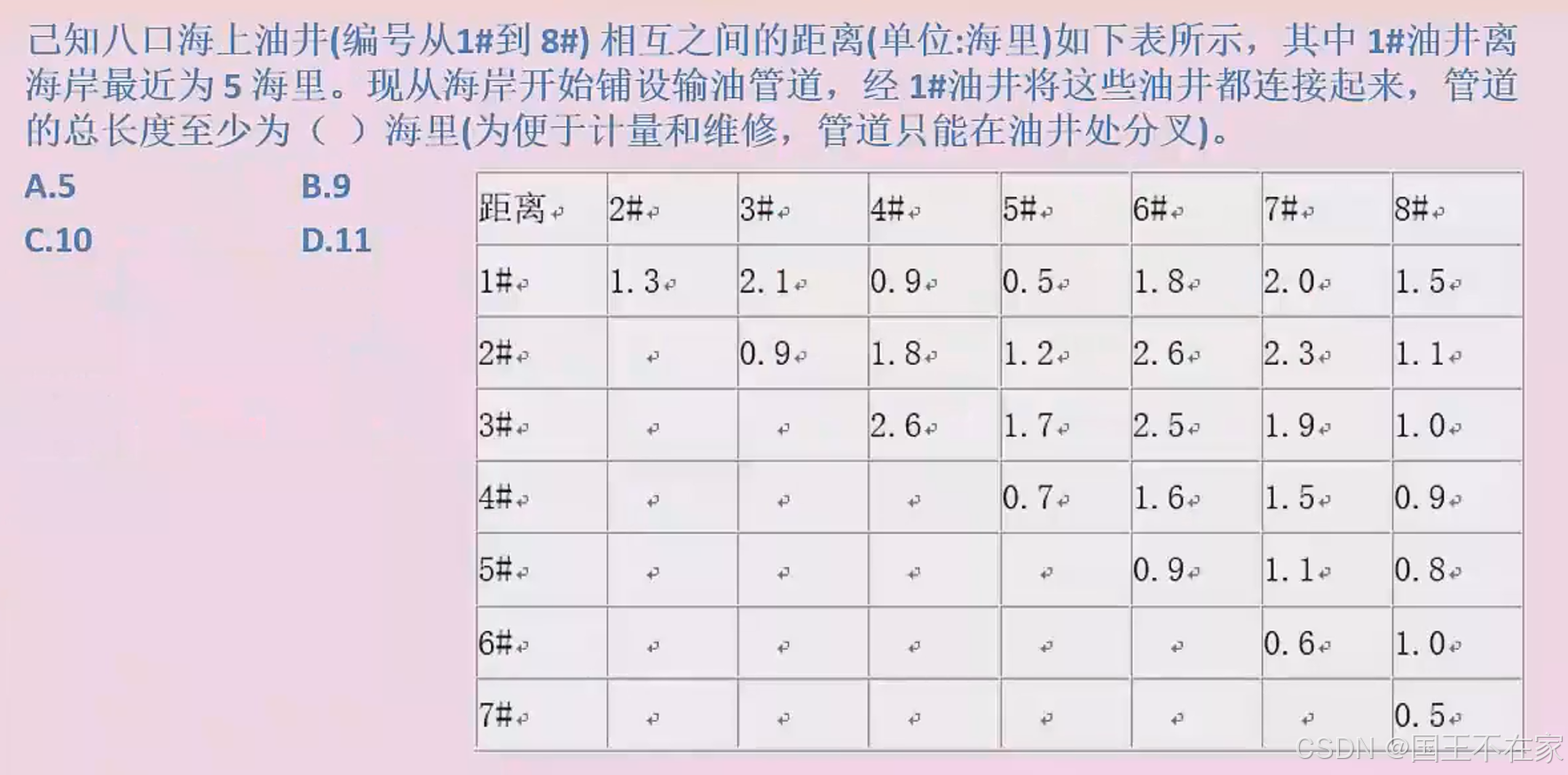
答案:C 10 不要忘记油井离陆地还有5海里。
最短路径
解法
最短路径是求起点到终点的最短路径。
关键路径是求起点到终点的最长路径,因为是求工期么,所以考虑最长的。
把每一步的距离求出来,到时候取最小的。
1、视频
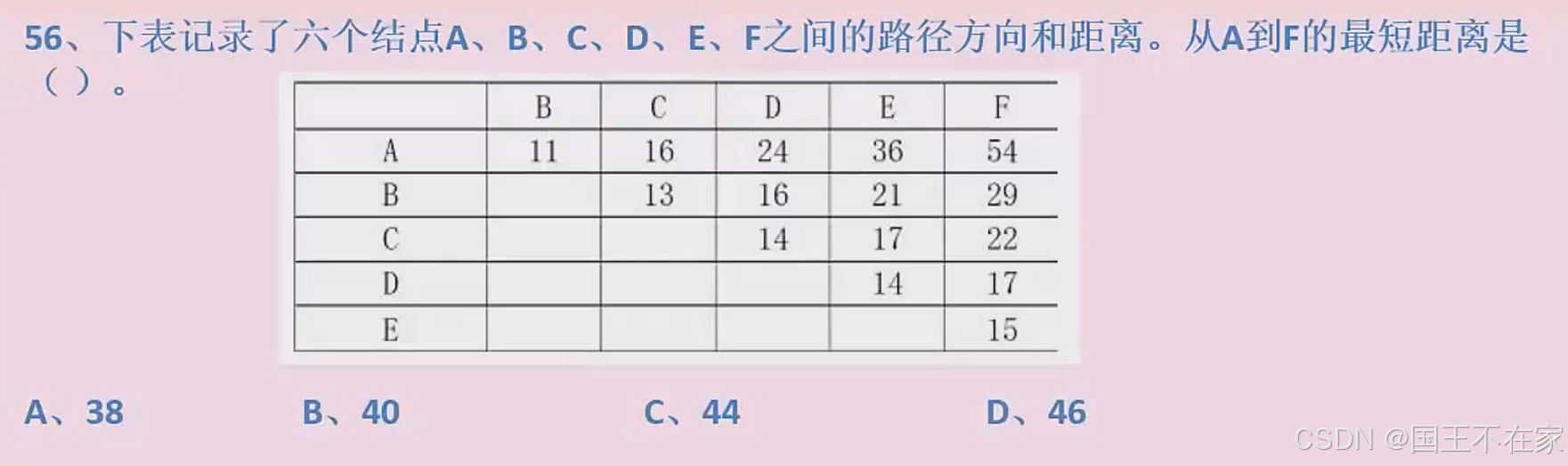
网络与最大流量
由路径的短板决定,从起点开始不断减少起点的输出。
1、视频
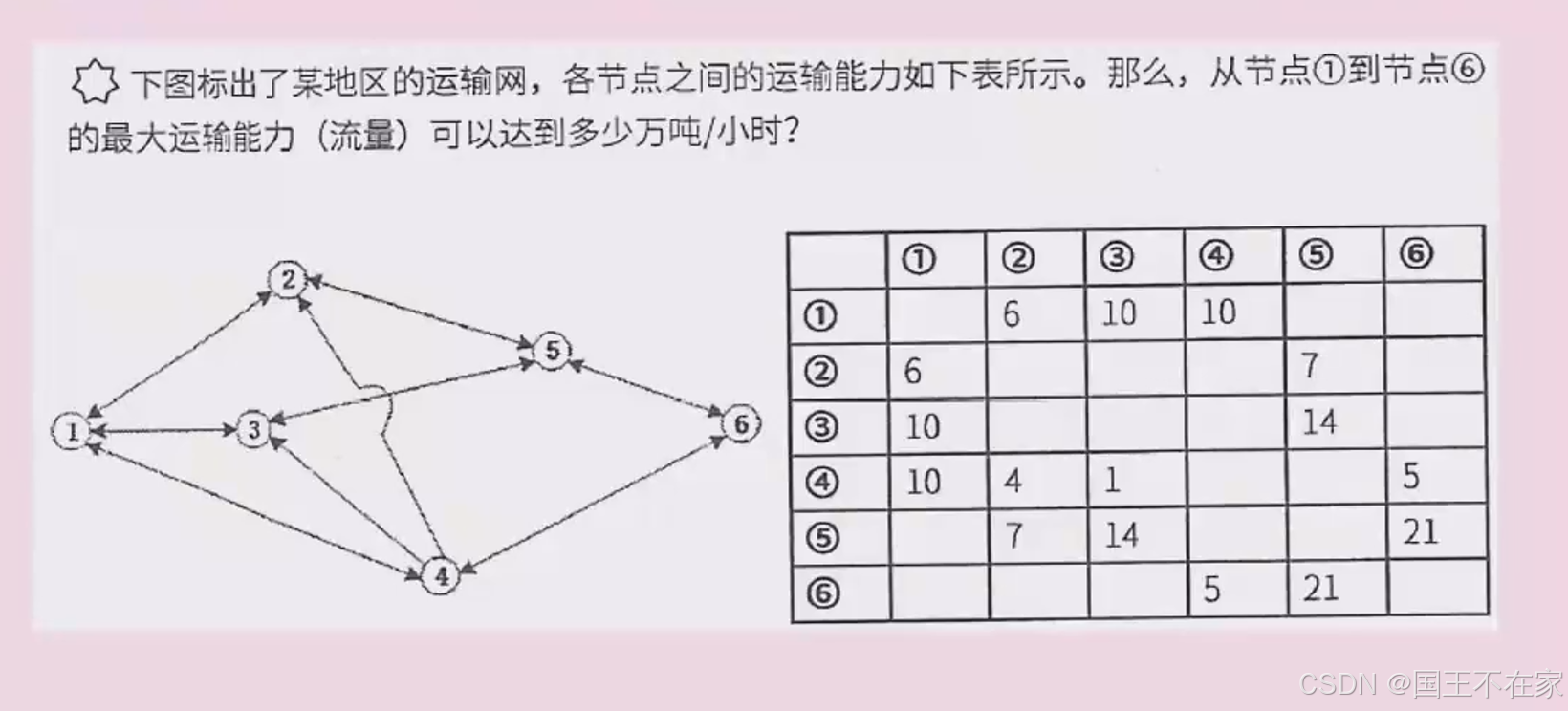
答案:23
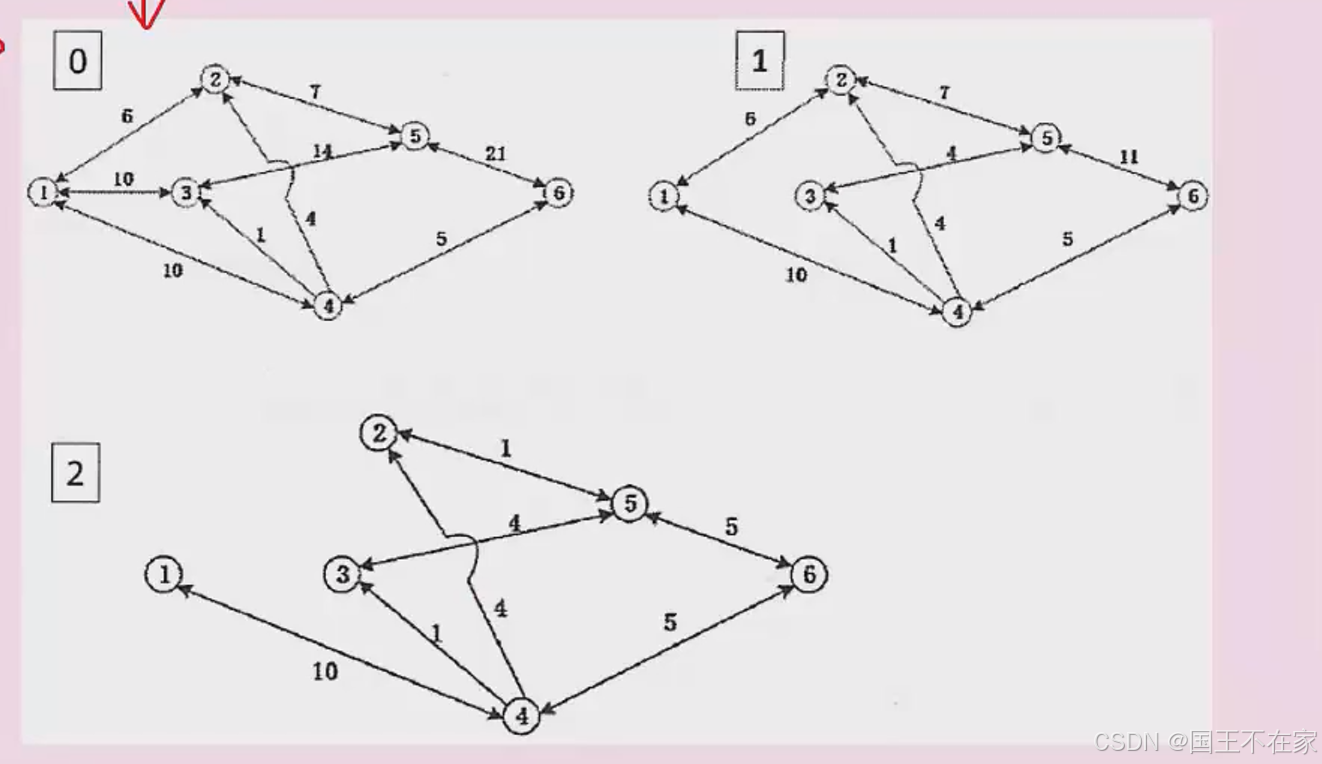
2、视频
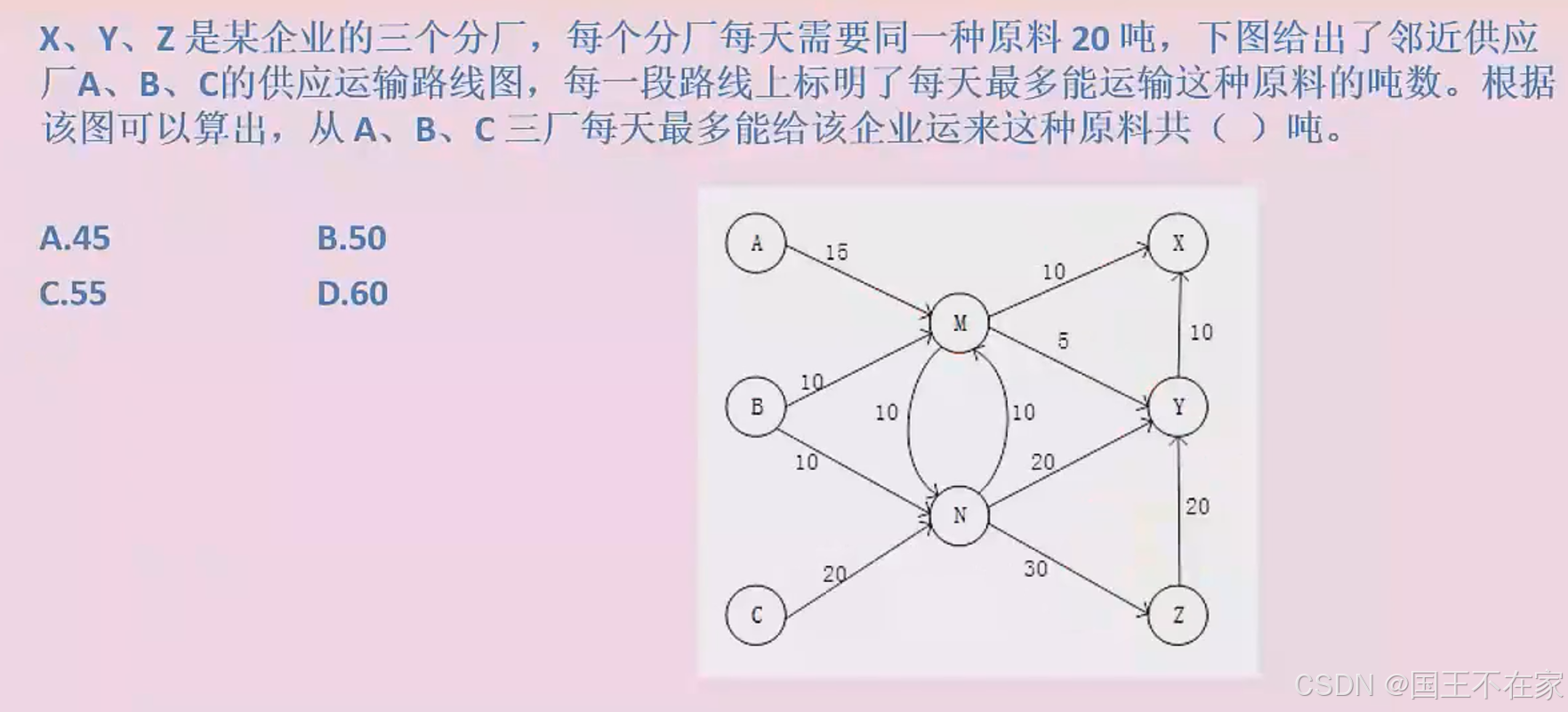
答案:55
线性规划
下面的文字也可能考察。
- 在一组约束条件下来寻找目标函数的极值(极大值和极小值)问题。
- 线性规划问题的数学模型通常由线性目标函数、线性约束条件、变量非负条件组成(实际问题中的变量一般都是非负的)。
- 线性规划问题就是面向实际应用,求解一组非负变量,使其满足给定的一组线性约束条件,并使某个线性目标函数达到极值。满足这些约束条件的非负变量组的集合称为可行解域。
- 可行解域中使目标函数达到极值的解称为最优解。
- 线性规划问题的最优解要么是0个(没有),要么是唯一的(1个),要么有无穷个(只要有2个,就会有无穷个)。
- 在实际应用中,可以直接求约束条件方程组的解,即是交叉点,将这些解代入到目标函数中判断是否极值即可。

连立2元1次方程组,两两求解,满足所有不等式
1、视频
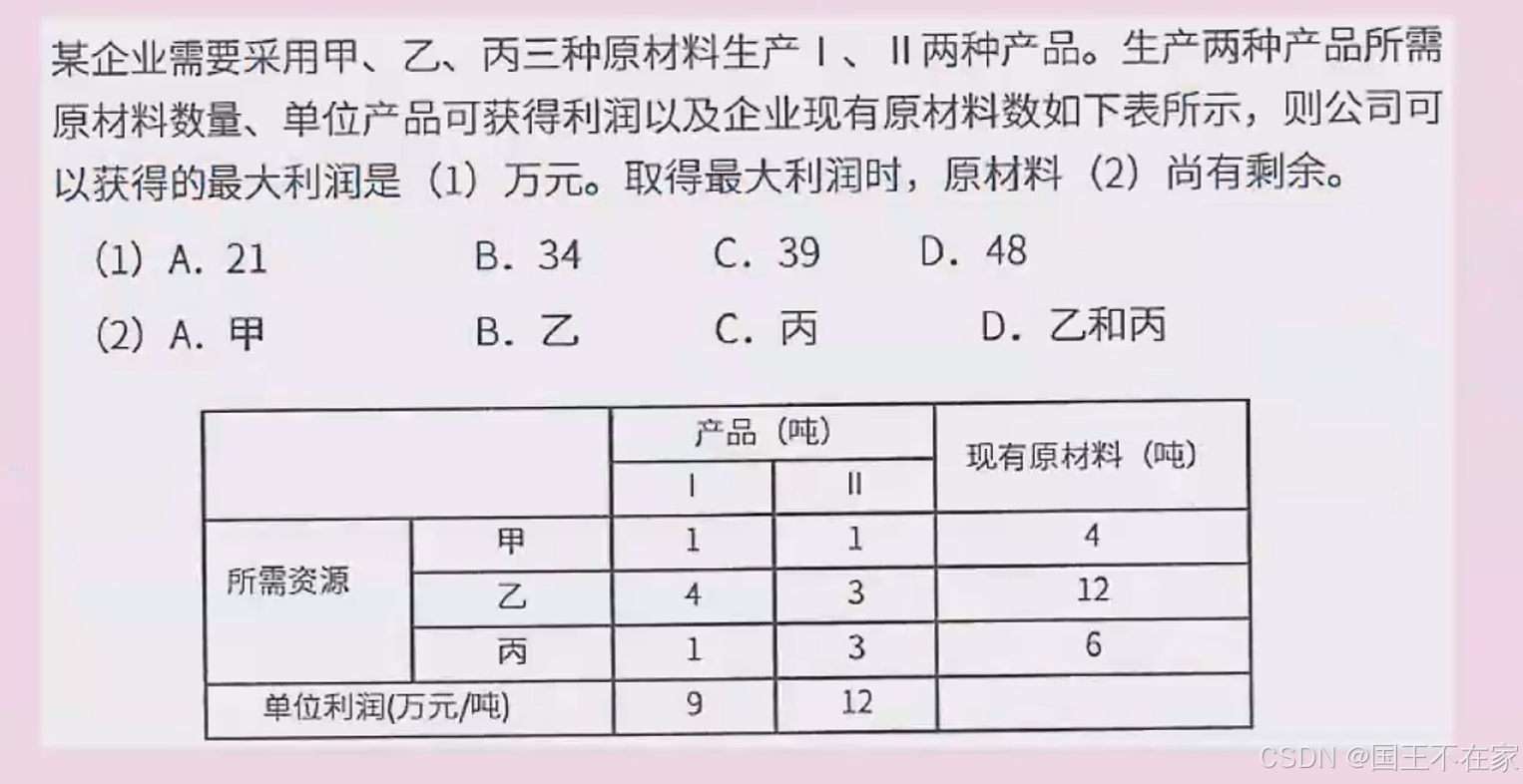

动态规划
直接穷举
1、视频
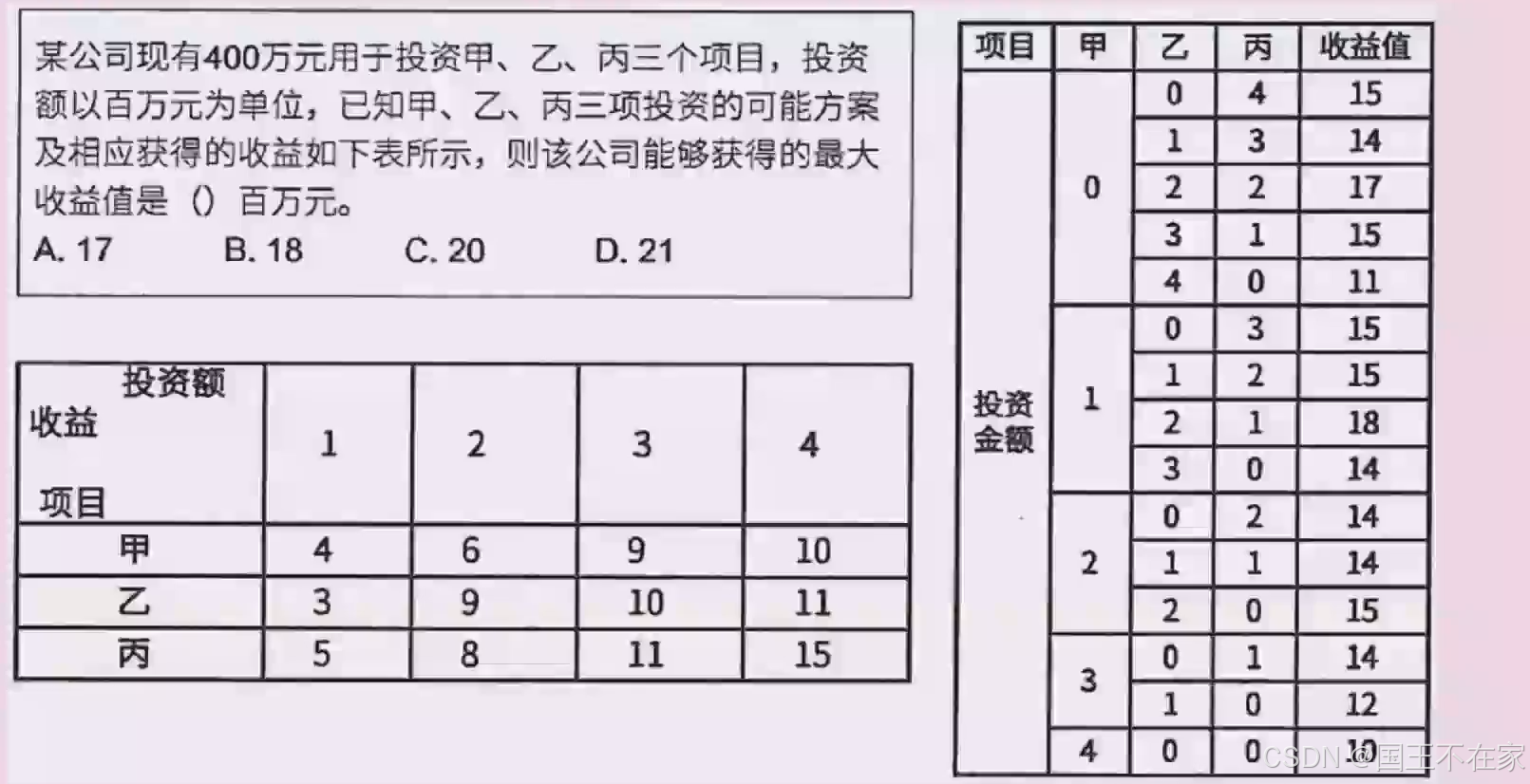
答案:18
2、视频

B
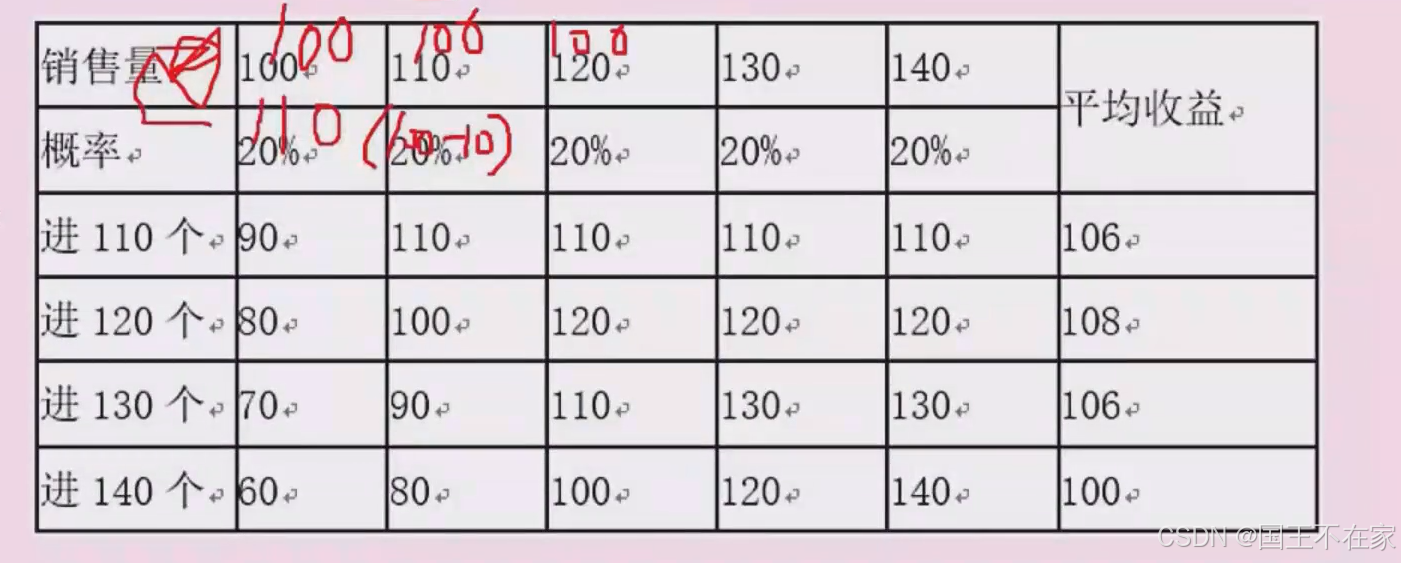
计算进110个、、、140个时,每天能卖出个数时赚的钱,最后再求一下平均。
3、视频-伏格尔
优先选用的最多还最小的。
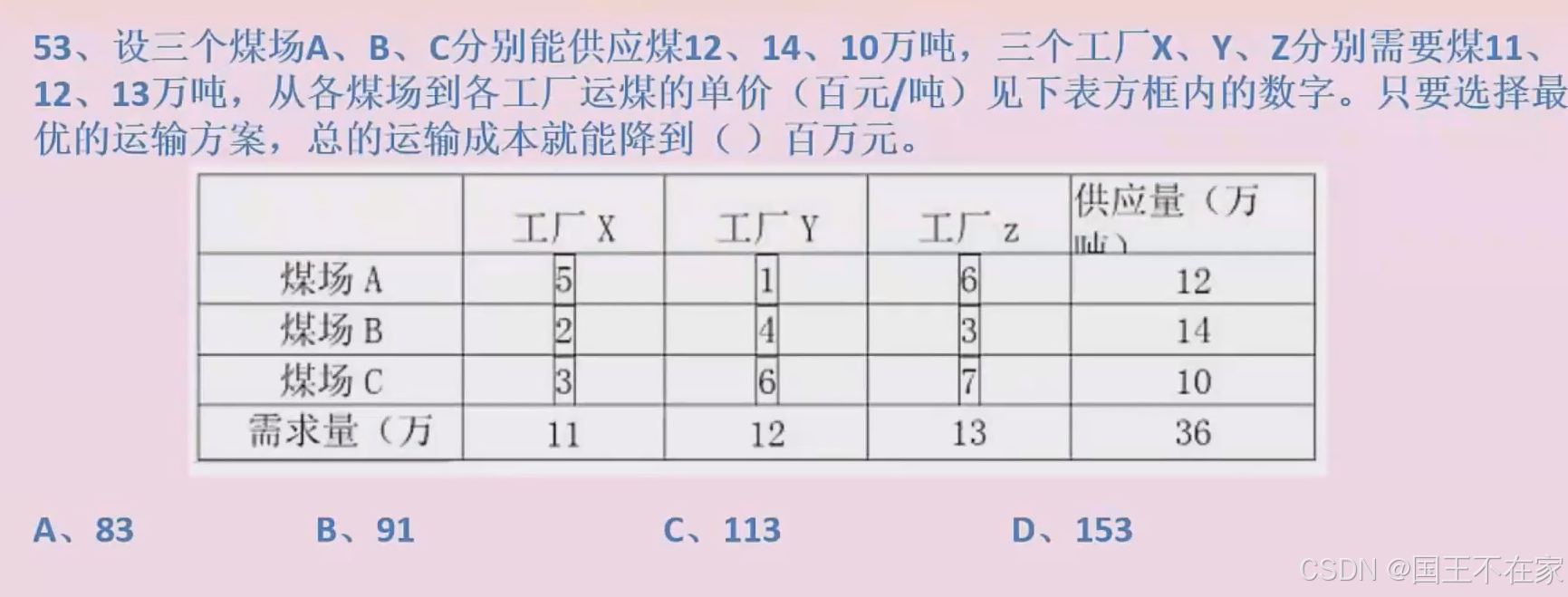
答案:A
博弈论
1、视频
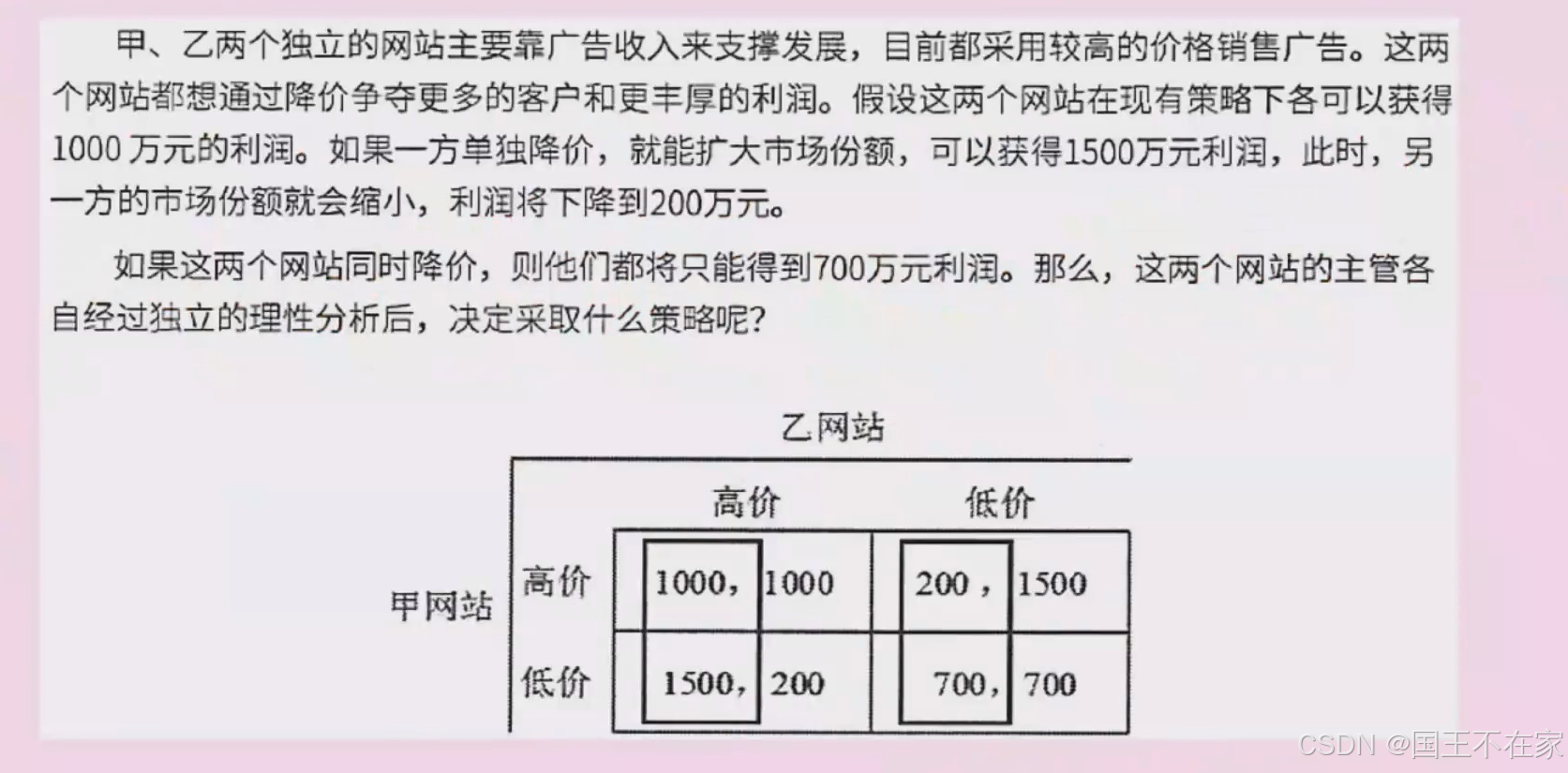
他们会同时降价。
状态转移矩阵
1、视频

A第一个月:0.5*0.8+0.5*0.4=0.6 ,B第一个月就是0.4
A第二个月:0.6*0.8+0.4*0.4 = 0.64
所以选C
排队
1、视频

答案:C
由题目可得三元一次方程组,还能得出20分钟的方程式,通过化解无关因子能得出16.

决策论

决策论的5种方案

1、视频
悲观是计算每个方案的最小收益,然后取这些收益的最大值。
乐观是计算每个方案的最大收益,再取这些收益的最大值。
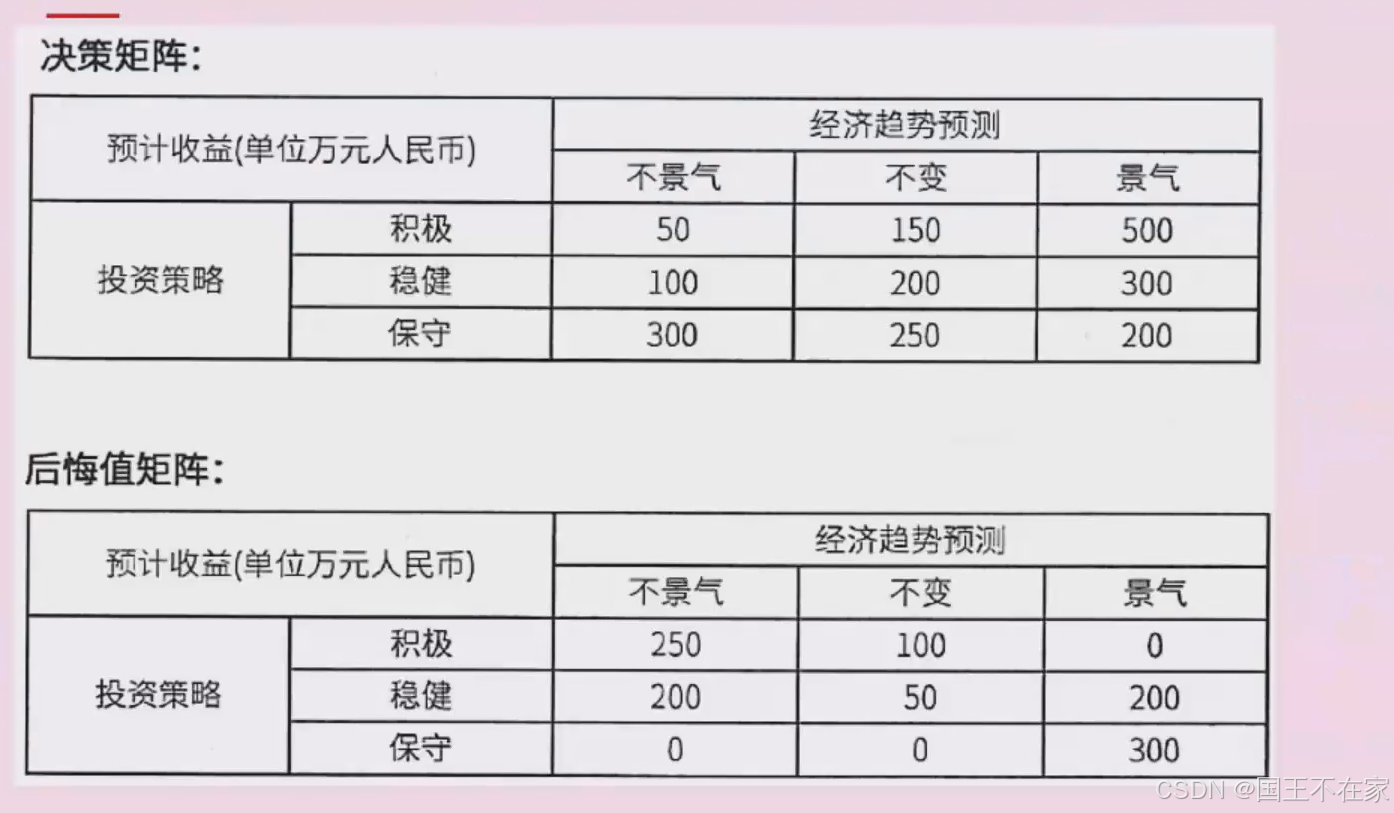
后悔值矩阵式先计算出后悔值:最大收益 减 最小收益,然后在后悔值中选出最小的就好了。
2、视频-决策树

数学建模
很早之前考的。


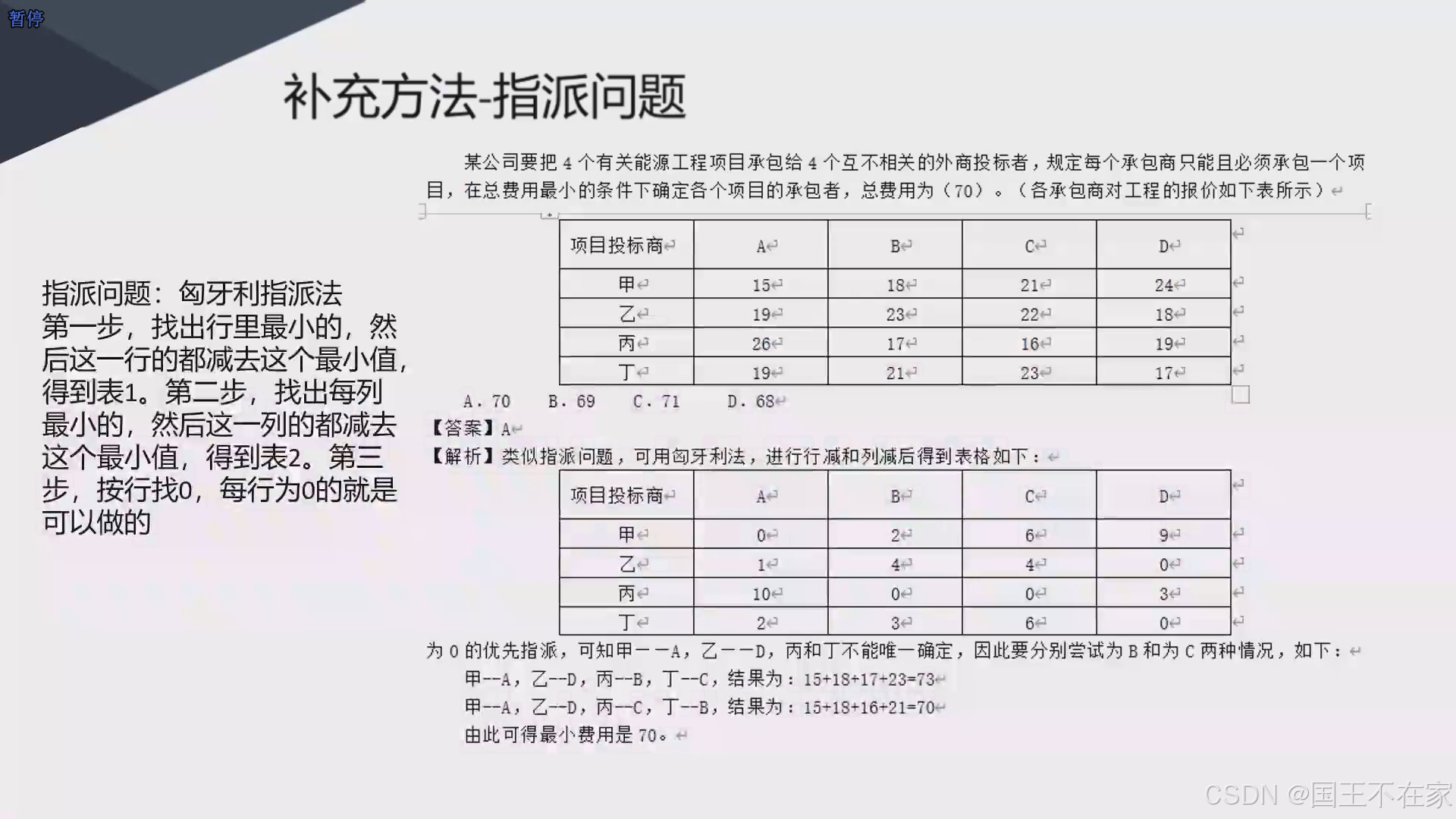
匈牙利指派
先每行减去最小,再每列减去最小的,然后优先使用每行只有一个0的数据。
可以用来解决动态规划的问题。