机器学习高级-day01-曲线拟合
从以下2个方面对曲线拟合进行介绍
1.曲线拟合算法理论讲解
2.编程实例与步骤
上面这2方面的内容,让大家,掌握并理解曲线拟合算法。
曲线拟合流程:
散点输入→前向计算→Sigmoid函数引入→参数初始化→损失函数→开始迭代→反向传播→显示频率设置→梯度下降显示
1 曲线拟合理论讲解
案例引入
1.1 散点输入
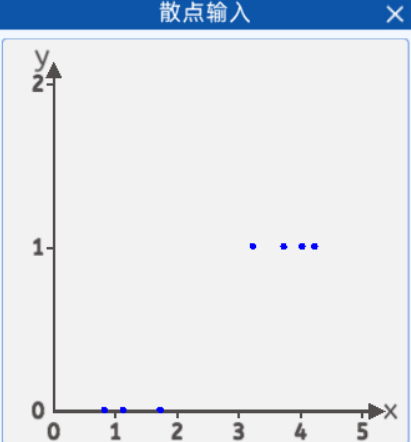
本实验中,采集了天数与是否觅食的的关系数据,x轴表示天数,y轴表示是否觅食,0表示不需要觅食,1表示需要觅食,从图上看有3只蝌蚪是不需要觅食的,3天以下的不需要觅食。有4只需要觅食,大于3天的需要觅食。并且将它们绘制在一个二维坐标中,其分布如下图所示:
坐标分别为[0.8, 0],[1.1, 0] ,[1.7, 0] ,[3.2, 1] ,[3.7, 1] ,[4.0, 1] ,[4.2, 1]。
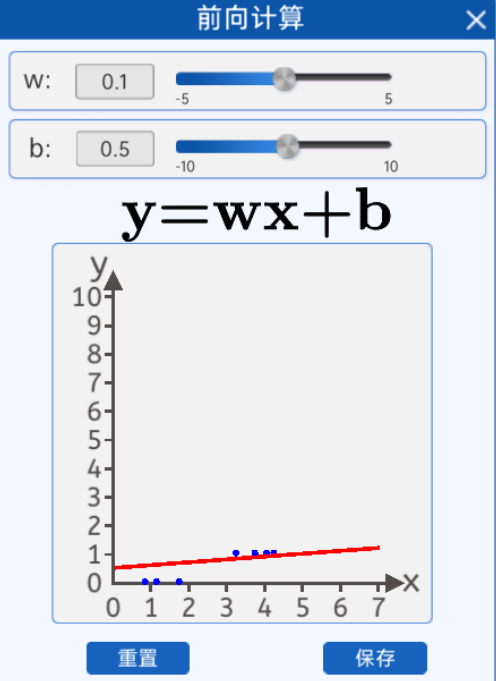
1.2 前向计算
我们的目的是拟合这些散点,通过前向计算,我们通过修改w和b只能部分点落在线上,从实验看直线无法拟合这些点。
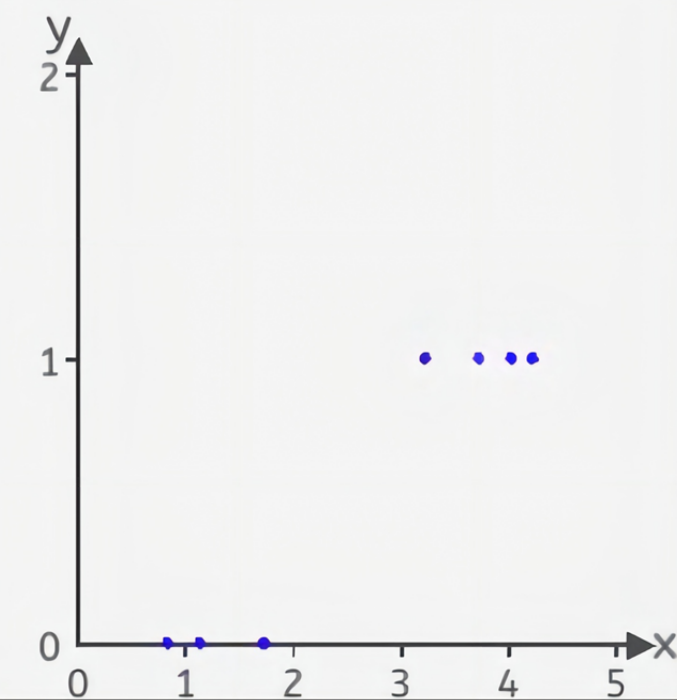
直线无法拟合那应该怎么办呢?
对于直线无法拟合这些点,是不是需要将直线变成曲线来拟合这些散点,在没有引入直线变曲线之前,使用直线是无法拟合这些点的。
 看到这个图,我们想着可以使用分段函数
看到这个图,我们想着可以使用分段函数
这个σ是一个激活函数。如果σ是阶跃函数,
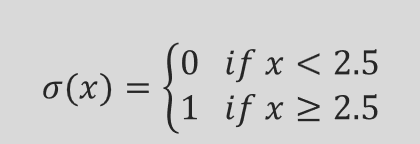
阶跃函数存在的问题?
不连续性:在x=2.5处不连续;
不可导性:在x=2.5处不存在导数;
怎么解决阶跃函数存在的问题呢?
我们是不是得找一个函数它要处处可微,是连续的,在各个地方都可导的,是不是就能很好的拟合当前曲线了。
阶跃函数可以作为激活函数吗?
阶跃函数(Step Function)可以作为激活函数,但在实际应用中并不常用。它的特点是:
定义:阶跃函数在某个阈值以下输出 0,在阈值以上输出 1。例如:
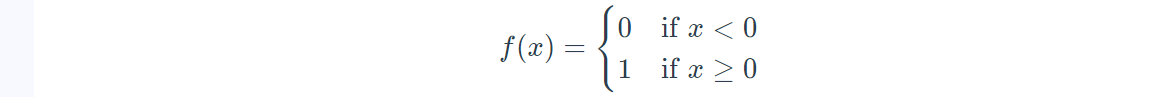
非连续性:阶跃函数是一个不连续的函数,这导致其在训练过程中无法计算梯度,因此不适合使用基于梯度的优化算法(如反向传播)。
局限性:由于其输出只有两种可能值,阶跃函数无法捕捉复杂的非线性关系,因此在深度学习中,通常选择如 ReLU、sigmoid 或 tanh 等激活函数,它们能够提供更平滑的梯度并支持更复杂的模型。
综上所述,尽管阶跃函数可以作为激活函数,但其缺乏梯度信息和灵活性使其在实际深度学习模型中不太适用。
1.3 Sigmoid函数引入
sigmoid拟合数据点效果图
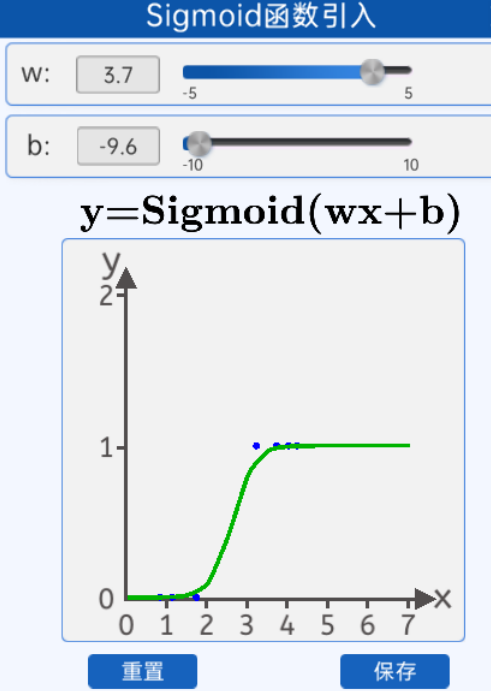
下面引入Sigmoid函数,当然是是前人慢慢发现的这个函数
Sigmoid的函数,其函数公式为:![]()
其函数图像如下所示:
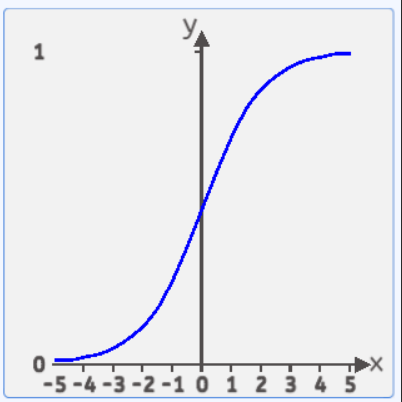
σ(x)的值域处于(0,1)之间,两边无限接近于0和1,但永远不等于0和1。定义域是负无穷到正无穷。
在线性回归中,直线的方程是![]() ,带入Sigmoid激活函数中,得到:
,带入Sigmoid激活函数中,得到:
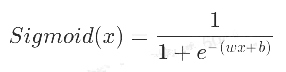
1.4 激活函数的引入
在该实验中,将直线转换成曲线,可以在直线 y=wx+b 加入一个新的函数 σ(wx+b) ,这个 σ 是一个激活函数,在上面实验中使用的激活函数是Sigmoid函数,当前还有其他激活函数,后面会讲。
激活函数是神经网络中一种重要的非线性函数,其作用在于引入非线性特性,使得神经网络能够学习和表示更加复杂的数据模式和关系。激活函数通常在每个神经元的输出上应用,将输入信号转换为输出信号。
以下是激活函数的主要作用:
-
引入非线性特性:如果在神经网络中只使用线性变换,例如线性加权和求和,那么整个网络的组合效果将仍然是线性的。激活函数的非线性特性能够在每个神经元上引入非线性转换,从而让神经网络能够学习和表示更加复杂的函数和数据模式。
-
提高模型的表达能力:激活函数的引入增加了神经网络的表达能力,使得网络可以逼近任何复杂的函数,这种特性称为“普遍逼近定理”(Universal Approximation Theorem)。
-
稀疏性和稳定性:一些激活函数(如Relu)具有稀疏性和稳定性的特点,可以缓解梯度消失和梯度爆炸的问题,从而有助于训练更深的神经网络。
梯度消失简单解释:w新=w旧-学习率*梯度 (梯度为0,w新一直等于w旧,引起w不更新就是梯度消失)
梯度爆炸简单解释:w新=w旧-学习率*梯度 (梯度非常大 ,只要大于1,因为模型会有很多层,链式求导法则需要连乘,就会导致梯度爆炸。)
综上所述,激活函数在神经网络中扮演着非常重要的角色,它们的引入使得神经网络具备非线性表达能力,从而能够处理和解决更加复杂的任务。
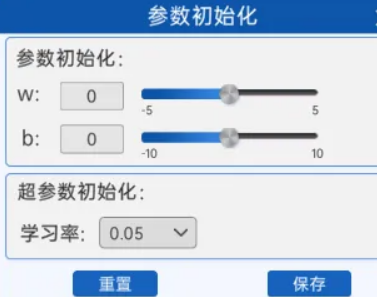
1.6 参数初始化
在之前的前向计算中,可以通过改变自己修改w和b来拟合这条曲线,但是在很多实际场景中,并没办法做到直接求出最优的w,b值,所以需要先随机定一个w和b,然后让梯度下降去拟合这些点。
在“参数初始化”组件中,可以初始化w和b的值以及学习率的值。
1.7 损失函数
根据公式: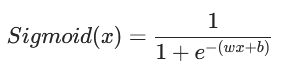
引入均方差损失函数中,于是损失函数就成了: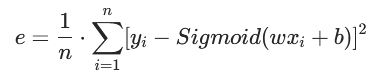

1.8 开始迭代
定义好损失函数后,选择好迭代次数,然后就可以进行反向传播了。
1.9 反向传播
在上面得到了损失函数的表达式,本实验中使用梯度下降的方式去降低损失函数值,于是需要对损失函数进行求导:![]()
将其拆分成复合函数,得到: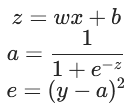
对复合函数求导,可得:
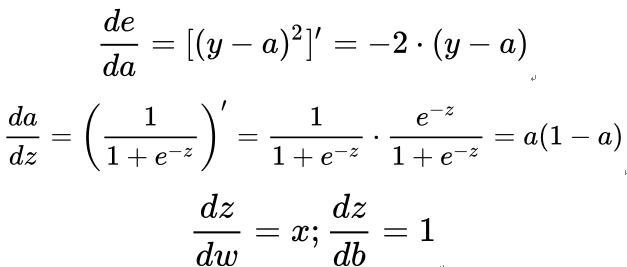

1.9 显示频率
通过设置显示频率,可以实时反馈当前的参数值和损失值。
1.10 梯度下降显示
通过可视化显示梯度下降
代码演示
# 1. 导入必要的库
import numpy as np # Python中用于科学计算的核心库,提供高效的数组操作和数学函数
import matplotlib.pyplot as plt # Python中常用的绘图库,用于数据可视化# 2. 准备数据
# 散点输入
data = np.array([[0.8, 0],[1.1, 0],[1.7, 0],[3.2, 1],[3.7, 1],[4.0, 1],[4.2, 1]])
"""
创建一个NumPy数组,包含7个数据点
每行表示一个数据点,第一列是特征值(x坐标),第二列是标签(0或1)
"""# 提取 x_data 和 y_data
x_data = data[:, 0] # 提取所有行的第一列作为特征
y_data = data[:, 1] # 提取所有行的第二列作为标签# 使用数组切片操作分离特征和标签# 前向计算 (当前步骤先写这里)
# 3. 定义Sigmoid激活函数
def sigmoid(x):"""Sigmoid激活函数的计算:param x::return: Sigmoid激活后的值"""return 1 / (1 + np.exp(-x))"""
Sigmoid函数将任意实数映射到(0,1)区间
在逻辑回归中,它用于将线性输出转换为概率值
数学公式:σ(x) = 1 / (1 + e^(-x))
"""# 4.参数初始化
w = 0 # 权重初始化为0
b = 0 # 偏置初始化为0
# 超参数初始化
learning_rate = 0.05 # 学习率设置为0.05
"""learning_rate控制每次参数更新的步长,是超参数需要手动设置"""# 开始迭代
# 5. 设置可视化画布
fig, (ax1, ax2) = plt.subplots(2, 1)
"""
创建一个2行1列的子图
ax1用于显示数据和决策边界
ax2用
于显示损失曲线
"""
# 6. 训练过程
# 需要用列表将迭代次数和损失保存起来。
epoch_list = [] # 存储训练轮次
loss_list = [] # 存储每轮的损失值
epochs = 5000 # 总训练轮数for epoch in range(1, epochs + 1):# 前向传播z = w * x_data + b # 计算线性部分a = sigmoid(z) # 应用Sigmoid激活函数得到预测概率# 计算损失(均方误差)loss = np.mean((y_data - a) ** 2)# 计算梯度(反向传播)deda = -2 * (y_data - a) # 损失对预测值的导数dadz = a * (1 - a) # Sigmoid函数的导数dzdw = x_data # 线性部分对w的导数dzdb = 1 # 线性部分对b的导数# 链式法则计算最终梯度gradient_w = np.mean(deda * dadz * dzdw)gradient_b = np.mean(deda * dadz * dzdb)# 更新参数 w新=w旧-lr(学习率)*G(梯度)w = float(w - learning_rate * gradient_w)b = float(b - learning_rate * gradient_b)# 记录训练过程,需要将epoch 和loss 存入到epoch_list 和loss_list中epoch_list.append(epoch)loss_list.append(loss)# 7.显示频率的设置(可视化部分)if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 显示图像# 画拟合的线# 获得x_data的最小值和x_data的最大值, 生成决策边界曲线x_min = x_data.min()x_max = x_data.max()# 按照等间隔获得从x_min到x_max之间的数据点# int((x_max - x_min) * 10) 想当于按照刻度来并取整x_values = np.linspace(x_min, x_max, int((x_max - x_min) * 10))# x_values有了,求y是不是通过下面的公式# np.round保留几位y_values = np.round(sigmoid(w * x_values + b), 3)# 画第一个图# 第1步 先清空ax1ax1.clear()# 第2步 画散点x_data 和y_dataax1.scatter(x_data, y_data)# 第3步 画线ax1.plot(x_values, y_values, c="r")ax1.set_title(f"Curve Regression: w={round(w, 3)}, b={round(b, 3)}")# 画第2个图# 第1步 先清空ax2ax2.clear()# 第2步 画loss曲线 epoch_list loss_listax2.plot(epoch_list, loss_list, color='r')ax2.set_xlabel("Epoch")ax2.set_ylabel("Loss")ax2.set_title(f"Loss Curve")# 显示图形plt.pause(0.1) # 暂停0.1秒,在此期间更新图形显示"""暂停程序执行:使程序暂停指定的时间(这里是0.1秒)更新图形显示:在暂停期间,Matplotlib 会处理所有待处理的图形事件,包括重绘图形实现动画效果:通过循环中的暂停,可以创建动态更新的可视化效果"""
plt.show()
# 显示图形。在循环结束后,保持图形窗口打开,以便查看最终结果。曲线拟合动态图_哔哩哔哩_bilibili
梯度计算过程(反向传播)
这段代码使用链式法则计算梯度:
deda = -2 * (y_data - a)
损失函数L = (y - a)²对预测值a的导数
这是均方误差的导数
dadz = a * (1 - a)
Sigmoid函数σ(z)对其输入z的导数
数学性质:σ'(z) = σ(z)(1 - σ(z))
dzdw = x_data 和 dzdb = 1
线性部分z = w*x + b对w和b的导数
最终梯度通过链式法则计算:
∂L/∂w = (∂L/∂a) × (∂a/∂z) × (∂z/∂w)
∂L/∂b = (∂L/∂a) × (∂a/∂z) × (∂z/∂b)
梯度下降更新规则
参数更新公式:参数 = 参数 - 学习率 × 梯度
学习率控制更新步长
太小的学习率会导致训练缓慢
太大的学习率可能导致无法收敛或震荡
可视化部分详解:
决策边界可视化
生成一组x值,覆盖数据范围
使用当前模型参数计算对应的y值(概率)
绘制这条曲线作为决策边界
损失曲线可视化
记录每个epoch的损失值
绘制损失随epoch变化的曲线
观察损失是否随着训练而下降
2 激活函数
从以下3个方面对激活函数及其导数进行介绍
1.激活函数及其导数算法理论讲解
2.编程实例与步骤
3.实验现象
通过上面这3方面的内容,掌握并理解激活函数及其导数算法。
2.1 激活函数及其导数算法理论讲解
2.1.1 激活函数的作用
激活函数的作用就是在神经网络中经过线性计算后,进行的非线性化。
下面讲解Sigmoid,tanh、Relu,Leaky Relu、Prelu、Softmax、ELU七种激活函数。
2.1.2 激活函数的概念
激活函数给神经元引入了非线性因素,让神经网络可以任意逼近任何非线性函数,通俗理解为把线性函数转换为非线性函数.
2.2 各激活函数及代码
2.2.1 Sigmoid
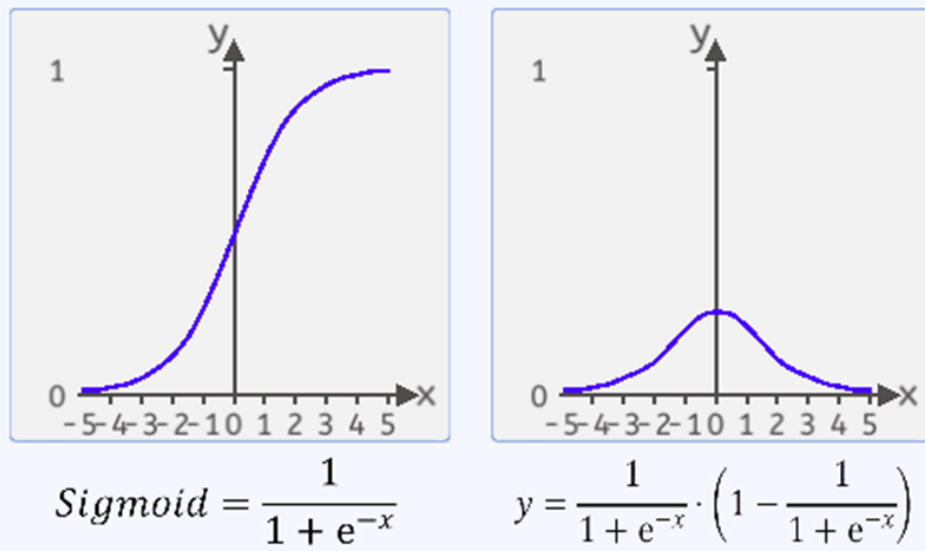
Sigmoid的函数公式为:![]()
函数图像如下图所示: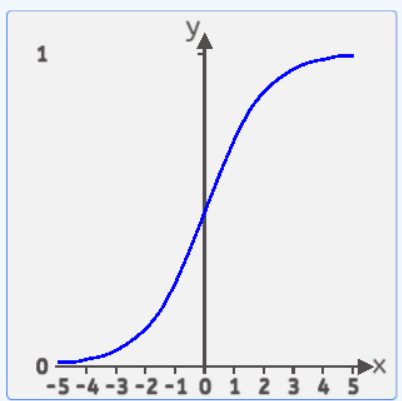
该函数处于(0,1)之间,两边无限接近于0和1,但永远不等于0和1。
sigmoid函数的导数公式为:![]()
导数图像为: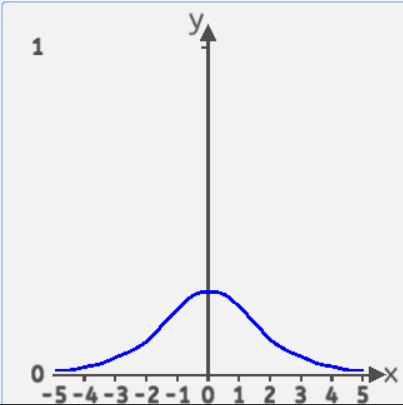
Sigmoid特点总结:
Sigmoid 函数的输出范围被限制在 0 到 1 之间,这使得它适用于需要将输出解释为概率或者介于 0 和 1 之间的任何其他值的场景。
Sigmoid 函数的两端,导数的值非常接近于零,这会导致在反向传播过程中梯度消失的问题,特别是在深层神经网络中。
Sigmoid激活函数有着如下几种缺点:
梯度消失:Sigmoid函数趋近0和1的时候变化率会变得平坦,从导数图像可以看出,当x值趋向两侧时,其导数趋近于0,在反向传播时,使得神经网络在更新参数时几乎无法学习到低层的特征,从而导致训练变得困难。
不以零为中心:Sigmoid函数的输出范围是0到1之间,它的输出不是以零为中心的,会导致其参数只能同时向同一个方向更新,当有两个参数需要朝相反的方向更新时,该激活函数会使模型的收敛速度大大的降低.
计算成本高:Sigmoid激活函数引入了exp()函数,导致其计算成本相对较高,尤其在大规模的深度神经网络中,可能会导致训练速度变慢。
不是稀疏激活:Sigmoid函数的输出范围是连续的,并且不会将输入变为稀疏的激活状态。在某些情况下,稀疏激活可以提高模型的泛化能力和学习效率。
Sigmoid代码
# 1. 导入必要的库
import numpy as np # Python中用于科学计算的核心库,提供高效的数组操作和数学函数
import matplotlib.pyplot as plt # Python中常用的绘图库,用于数据可视化# 2. 准备数据
# 散点输入
data = np.array([[0.8, 0],[1.1, 0],[1.7, 0],[3.2, 1],[3.7, 1],[4.0, 1],[4.2, 1]])
"""
创建一个NumPy数组,包含7个数据点
每行表示一个数据点,第一列是特征值(x坐标),第二列是标签(0或1)
"""# 提取 x_data 和 y_data
x_data = data[:, 0] # 提取所有行的第一列作为特征
y_data = data[:, 1] # 提取所有行的第二列作为标签# 使用数组切片操作分离特征和标签# 前向计算 (当前步骤先写这里)
# 3. 定义Sigmoid激活函数
def sigmoid(x):"""Sigmoid激活函数的计算:param x::return: Sigmoid激活后的值"""return 1 / (1 + np.exp(-x))"""
Sigmoid函数将任意实数映射到(0,1)区间
在逻辑回归中,它用于将线性输出转换为概率值
数学公式:σ(x) = 1 / (1 + e^(-x))
"""# 4.参数初始化
w = 0 # 权重初始化为0
b = 0 # 偏置初始化为0
# 超参数初始化
learning_rate = 0.05 # 学习率设置为0.05
"""learning_rate控制每次参数更新的步长,是超参数需要手动设置"""# 开始迭代
# 5. 设置可视化画布
fig, (ax1, ax2) = plt.subplots(2, 1)
"""
创建一个2行1列的子图
ax1用于显示数据和决策边界
ax2用
于显示损失曲线
"""
# 6. 训练过程
# 需要用列表将迭代次数和损失保存起来。
epoch_list = [] # 存储训练轮次
loss_list = [] # 存储每轮的损失值
epochs = 5000 # 总训练轮数for epoch in range(1, epochs + 1):# 前向传播z = w * x_data + b # 计算线性部分a = sigmoid(z) # 应用Sigmoid激活函数得到预测概率# 计算损失(均方误差)loss = np.mean((y_data - a) ** 2)# 计算梯度(反向传播)deda = -2 * (y_data - a) # 损失对预测值的导数dadz = a * (1 - a) # Sigmoid函数的导数dzdw = x_data # 线性部分对w的导数dzdb = 1 # 线性部分对b的导数# 链式法则计算最终梯度gradient_w = np.mean(deda * dadz * dzdw)gradient_b = np.mean(deda * dadz * dzdb)# 更新参数 w新=w旧-lr(学习率)*G(梯度)w = float(w - learning_rate * gradient_w)b = float(b - learning_rate * gradient_b)# 记录训练过程,需要将epoch 和loss 存入到epoch_list 和loss_list中epoch_list.append(epoch)loss_list.append(loss)# 7.显示频率的设置(可视化部分)if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 显示图像# 画拟合的线# 获得x_data的最小值和x_data的最大值, 生成决策边界曲线x_min = x_data.min()x_max = x_data.max()# 按照等间隔获得从x_min到x_max之间的数据点# int((x_max - x_min) * 10) 想当于按照刻度来并取整x_values = np.linspace(x_min, x_max, int((x_max - x_min) * 10))# x_values有了,求y是不是通过下面的公式# np.round保留几位y_values = np.round(sigmoid(w * x_values + b), 3)# 画第一个图# 第1步 先清空ax1ax1.clear()# 第2步 画散点x_data 和y_dataax1.scatter(x_data, y_data)# 第3步 画线ax1.plot(x_values, y_values, c="r")ax1.set_title(f"Curve Regression: w={round(w, 3)}, b={round(b, 3)}")# 画第2个图# 第1步 先清空ax2ax2.clear()# 第2步 画loss曲线 epoch_list loss_listax2.plot(epoch_list, loss_list, color='r')ax2.set_xlabel("Epoch")ax2.set_ylabel("Loss")ax2.set_title(f"Loss Curve")# 显示图形plt.pause(0.1) # 暂停0.1秒,在此期间更新图形显示"""暂停程序执行:使程序暂停指定的时间(这里是0.1秒)更新图形显示:在暂停期间,Matplotlib 会处理所有待处理的图形事件,包括重绘图形实现动画效果:通过循环中的暂停,可以创建动态更新的可视化效果"""
plt.show()
# 显示图形。在循环结束后,保持图形窗口打开,以便查看最终结果。代码运行结果:Sigmoid.png
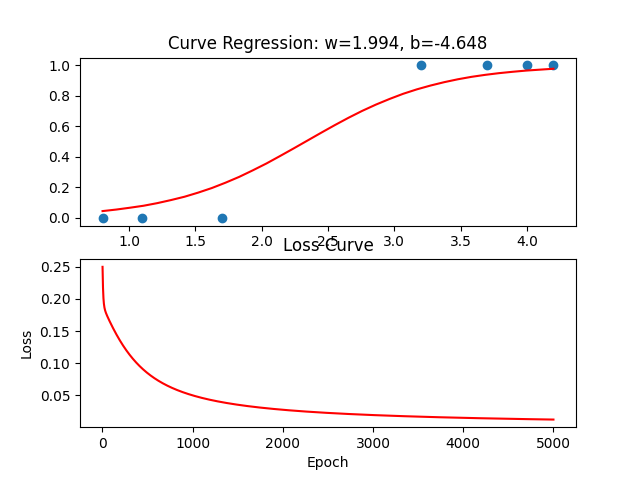
2.2.2 tanh
tanh:双曲正切的激活函数。
tanh激活函数的数学公式为: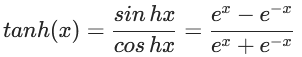
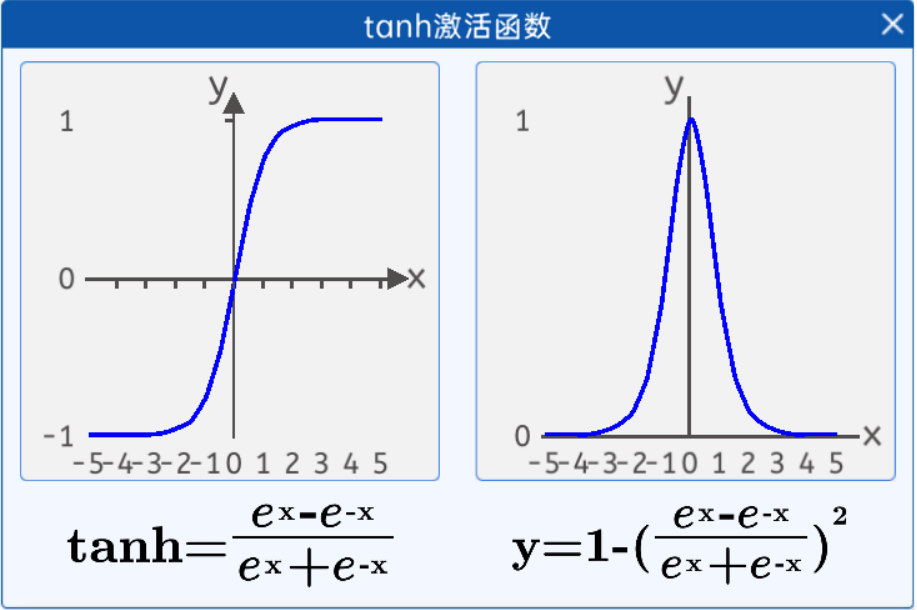
该函数解决了Sigmoid函数不以零为中心的问题,它的取值范围是(-1,1),无限接近1和-1,但永不等于1或者-1,它是关于0中心对称,以零为中心。
tanh导数公式为: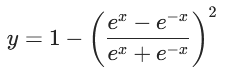
tanh特点总结:
输出范围:tanh 函数的输出范围被限制在 -1 到 1 之间,因此它可以使神经网络的输出更接近于零中心,有助于减少梯度消失问题。
零中心性:tanh 函数的输出以零为中心,即在输入为 0 时函数值为 0,这有助于减少梯度消失问题,并使得神经网络更容易学习。
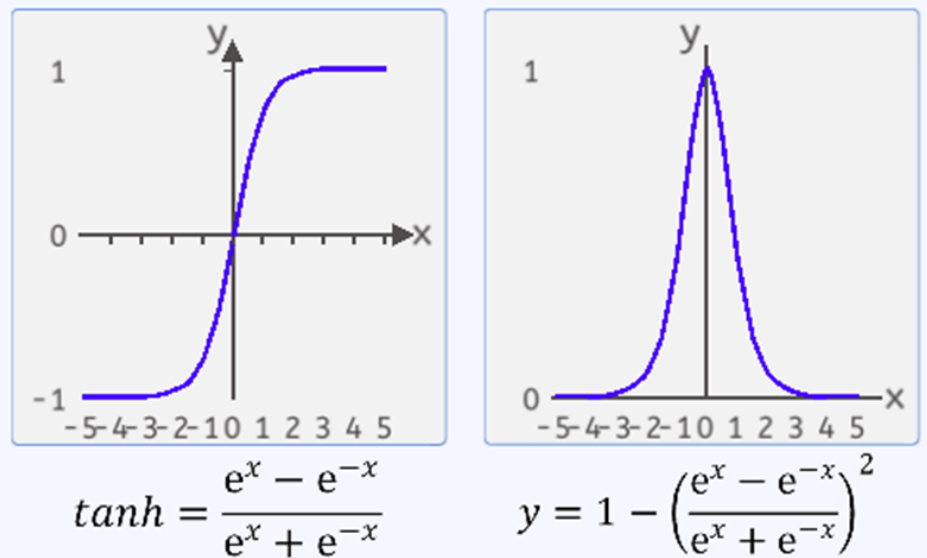
相对于Sigmoid函数,优势显而易见:
输出以零为中心:tanh函数的输出范围是-1到1之间,其均值为零,因此它是零中心的激活函数。相比于Sigmoid函数,tanh函数能够更好地处理数据的中心化和对称性,有助于提高网络的学习效率。
饱和区域更大:在输入绝对值较大时,tanh函数的斜率较大,这使得它在非线性变换上比Sigmoid函数更加陡峭,有助于提供更强的非线性特性,从而提高了网络的表达能力。
良好的输出范围:tanh函数的输出范围在-1到1之间,相比于Sigmoid函数的0到1之间,输出范围更广,有助于减少数据在网络中传播时的数值不稳定性。
但是缺点也同样明显:
容易出现梯度消失问题:虽然相比于Sigmoid函数,tanh函数在非饱和区域的斜率较大,但在输入绝对值较大时,其导数仍然会接近于零,可能导致梯度消失问题。
计算难度同样大。
# 1.导入必要的库
import numpy as np
import matplotlib.pyplot as plt# 2.定义tanh函数
def tanh(x):# 使用numpy自带的tanh函数return np.tanh(x)"""定义了一个tanh函数,它直接调用NumPy库中的tanh函数tanh(双曲正切)函数将输入值映射到(-1, 1)区间公式为:tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
"""# 3.计算tanh函数的导数
def tanh_derivative(x):return 1 - np.tanh(x) ** 2"""tanh函数的导数为1 - tanh²(x)这是通过链式法则推导得到的
"""# 4.创建输入数据
x = np.linspace(-10, 10, 100)
"""
使用linspace函数创建一个从10到10的等间距数组,包含100个点
这些点将作为我们绘制函数图像的x坐标
"""# 5.计算每个x点对应的tanh函数值
y_tanh = tanh(x) # 结果存储在y_tanh数组中
# 计算每个x点对应的tanh导数函数值
y_derivative = tanh_derivative(x) # 结果存储在y_derivative数组中# 6.绘制tanh函数图像
plt.figure(figsize=(8, 6)) # 创建一个新的图形窗口,设置大小为8×6英寸
plt.plot(x, y_tanh, label="tanh")
"""绘制tanh函数曲线,x为横坐标,y_tanh为纵坐标label参数设置图例中显示的标签
"""
plt.plot(x, y_derivative, label="tanh_derivative") # 绘制tanh导数函数曲线
plt.title("tanh and tanh_derivative") # 设置图形的标题
plt.legend() # 显示图例,标识每条曲线代表什么函数
plt.grid(True) # 添加网格线,使图表更易读
plt.savefig('tanh.png')
plt.show() # 显示图形窗口"""
梯度是一个向量,表示函数在某一点处变化率最大的方向和大小。
对于单变量函数,梯度就是导数;
对于多变量函数,梯度是各个偏导数组成的向量。梯度的意义方向:梯度指向函数值增长最快的方向大小:梯度的模表示函数在该方向上的变化率
"""代码运行结果:tanh.png
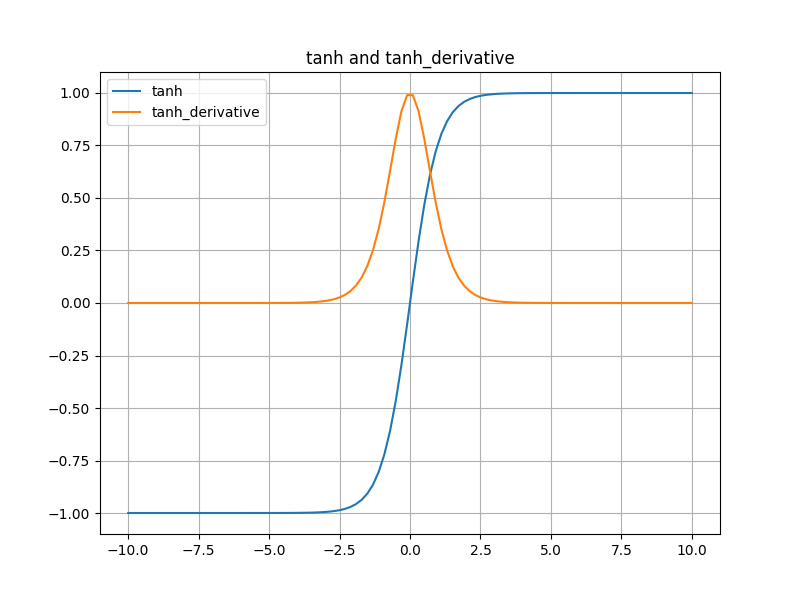
2.2.3 ReLU
2012年Alexnet提出的激活函数ReLU
ReLU激活函数的数学公式为:![]()
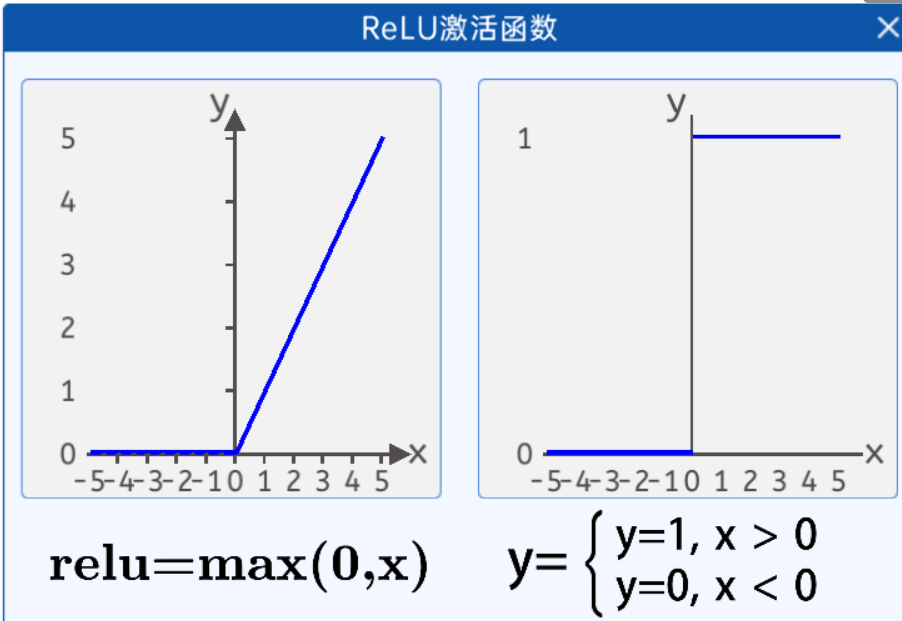
ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变。
ReLU函数的导数公式为: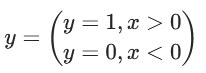
ReLU特点:
稀疏性:ReLU 函数的导数在输入为负数时为零,这意味着在反向传播过程中,只有激活的神经元会传递梯度,从而促进了稀疏激活的现象,有助于减少过拟合。
计算高效:ReLU 函数的计算非常简单,并且在实践中被证明是非常高效的。
解决梯度消失问题: ReLU函数在输入大于零时输出其本身值,这使得在反向传播时梯度保持为常数1,避免了梯度消失问题。ReLU函数在深度网络中更容易训练。
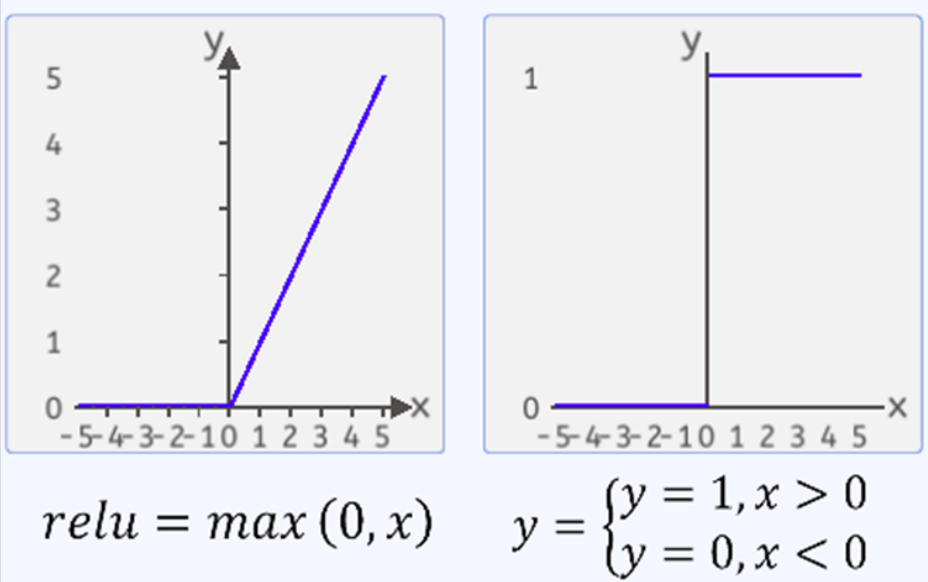
ReLU函数的优势:
解决梯度消失问题: ReLU函数在输入大于零时输出输入值,这使得在反向传播时梯度保持为常数1,避免了梯度消失问题。相比于Sigmoid和tanh函数,ReLU函数在深度网络中更容易训练,使得网络能够更有效地学习复杂的特征。
计算速度快: ReLU函数的计算非常简单,只需进行一次阈值判断和取最大值操作。这使得在大规模深度神经网络中,ReLU函数的计算速度远快于Sigmoid和tanh函数,加快了模型训练的速度。
稀疏激活性: 在输入小于零的情况下,ReLU函数的输出是零,这表现为稀疏激活性。这意味着在激活后,一部分神经元将被激活,而其他神经元则保持不活跃。这有助于减少神经网络中的冗余计算和参数数量,提高了网络的泛化能力。
它的劣势:
死亡ReLU问题(Dying ReLU): 在训练过程中,某些神经元可能会遇到“死亡ReLU”问题,即永远不会被激活。如果某个神经元在训练过程中的权重更新导致在其上的输入始终为负值,那么它的输出将永远为零。这意味着该神经元不会再学习或参与后续训练,导致该神经元“死亡”,从而减少了网络的表达能力。
死亡relu问题理解
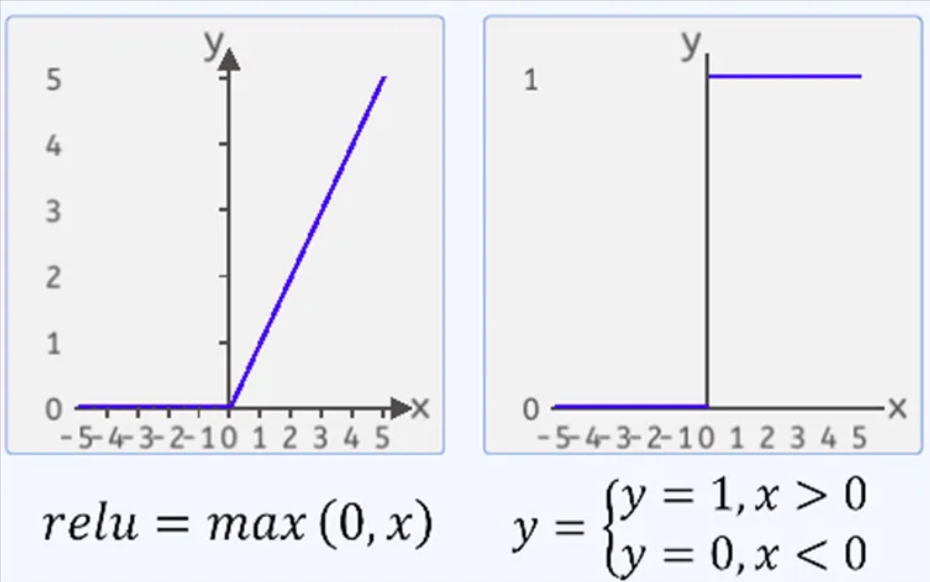
ReLU函数梯度只可以取两个值,当输入小于0时,梯度为0;当输入大于0时,梯度为1,在反向传播过程中,
(w新=w旧-学习率*梯度),如果学习率比较大,一个很大的梯度更新后,经过Relu激活函数,可能会导致ReLU神经元更新后的梯度是负数,进而导致下一轮正向传播过程中ReLU神经元的输入是负数,输出是0,由于ReLU神经元的输出为0,在后续迭代的反向过程中,该处的梯度一直为0,相关参数不再变化,从而导致ReLU神经元的输入始终是负数,输出始终为0。即为“死亡ReLU问题”。
输出不是以零为中心: ReLU函数的输出范围是从零开始,因此输出不是以零为中心的。这可能会导致训练过程中的参数更新存在偏差,降低了网络的优化能力。
不适合所有问题: 尽管ReLU函数在大多数情况下表现良好,但并不是适合所有问题。对于一些问题,特别是在处理一些包含负值的数据时,ReLU函数可能不够理想,可能会产生不良的结果。
针对ReLU函数的劣势,研究人员也提出了一些改进的激活函数,如Leaky ReLU、Parametric ReLU和Exponential Linear Units(ELU)等,这些函数在一定程度上缓解了ReLU函数的问题,并在特定情况下表现更好。因此,在实际使用中,根据具体问题和实验结果选择合适的激活函数是很重要的。
# 1.导入必要的库
import numpy as np
import matplotlib.pyplot as plt# 2.定义ReLU激活函数
def relu(x):# np.maximun逐位比较array1和array2,并输入两者的最大值return np.maximum(0, x) # 返回x和0之间的较大值# 3.定义ReLU函数的导数
def relu_derivative(x):# np.where根据条件选择返回值# 当x>0时返回1,否则返回0return np.where(x > 0, 1, 0)# 4.定义x的范围:从-10到10之间均匀生成100个点
x = np.linspace(-10, 10, 100)# 5.# 计算ReLU函数和ReLU导数在这些点上的值
y_relu = relu(x)
y_derivative = relu_derivative(x)# 6.创建ReLU函数图像
plt.figure(figsize=(8, 6)) # 创建图形,设置图形大小为8×6英寸
plt.plot(x, y_relu, label='relu') # 绘制ReLU函数曲线,并添加标签
plt.plot(x, y_derivative, label='relu_derivative') # 绘制ReLU导数曲线,并添加标签
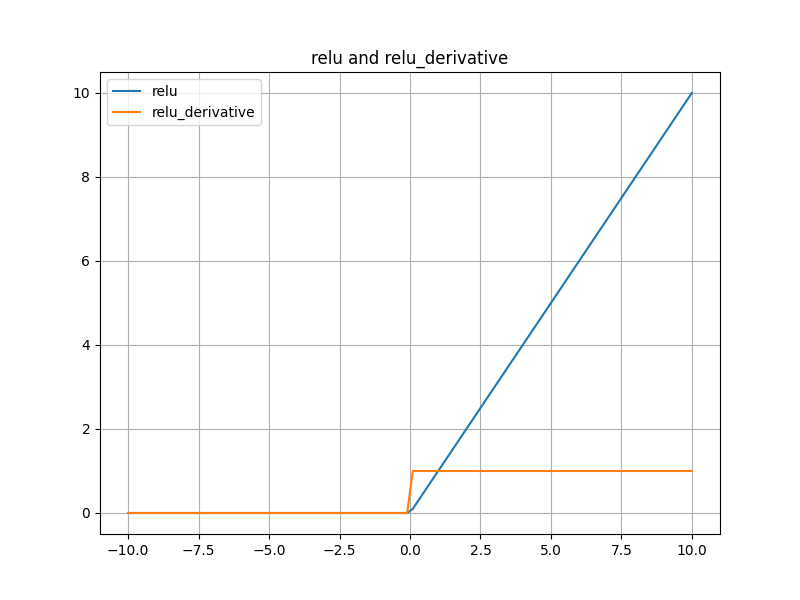
plt.title('relu and relu_derivative') # 设置图表标题
plt.legend() # 显示图例
plt.grid(True) # 显示网格线
plt.savefig('ReLU.png')
plt.show() # 显示图形代码运行结果:ReLU.png
2.2.4 Leaky Relu
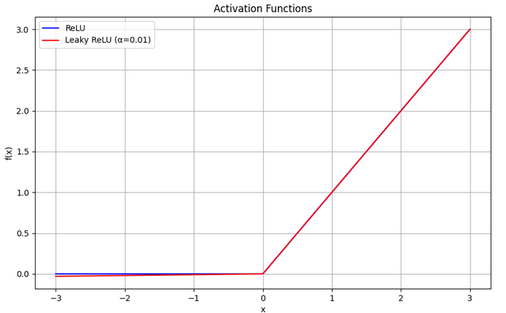
公式:f(x)=max(αx, x),其中 α 是一个小常数(例如0.01)
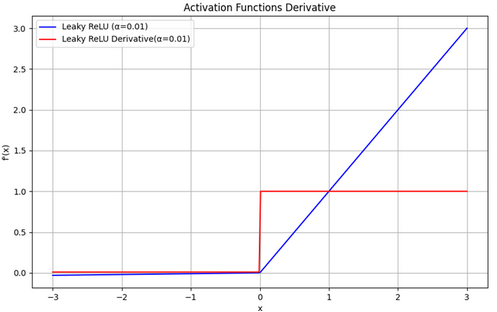
导数:
f’(x)=1,当x>0时。
f’(x)=α,当x<=0时。
Leaky ReLU 通过在负数区域引入小的正斜率 α 来避免ReLU的“死亡”问题,允许负数区域的梯度不为零。
# 1.导入必要的库
import numpy as np
import matplotlib.pyplot as plt# 2.定义ReLU激活函数
def relu(x):return np.maximum(0, x)"""
np.maximum(0,x):逐元素比较0和x中的值,返回较大的值
当x>0时返回x,否则返回0
"""# 3.定义Leaky ReLU激活函数
def leaky_relu(x, alpha=0.01):return np.where(x > 0, x, x * alpha)"""
np.where(condition, x, y):根据条件选择返回值,条件为真时返回x,否则返回y
当x>0时返回x,否则返回x*alpha(alpha是一个小的正数,默认0.01)
"""# 4.定义Leaky ReLU的导数函数
def leak_relu_derivative(x, alpha=0.01):return np.where(x > 0, 1, alpha) # 当x>0时返回1,否则返回alpha# 5.创建输入数据
x = np.linspace(-3, 3, 100) # 创建一个从-3到3的等间距数组,包含100个点# # 6.绘制第一个图形窗口,绘制ReLU和Leaky ReLU函数的图像
# plt.figure(figsize=(8, 6)) # 创建一个新的图形窗口,设置大小为8×6
# plt.plot(x, relu(x), label="relu") # 绘制 ReLU函数的曲线
# """
# x: 横坐标值(输入值)
# leaky_relu(x): 纵坐标值(函数输出值)
# label: 设置图例中显示的标签文本
# """
#
# plt.plot(x, leaky_relu(x), label="leaky_relu alpha=0.01") # 绘制Leaky ReLU的曲线
# """
# 使用相同的横坐标x
# leak_relu_derivative(x): 纵坐标值(导数输出值)
# """
#
# plt.title("relu and leaky_relu alpha=0.01") # 设置图形的标题
# plt.legend() # 显示图例,位置自动选择最佳位置,图例内容来自上面两个plot语句的label参数
# plt.grid(True) # 在图形上显示网格线,便于观察和读取数值
# plt.show() # 显示图形窗口
#
# # 7.创建第二个图形窗口,绘制Leaky ReLU函数及其导数的图像
# plt.figure(figsize=(8, 6)) # 创建一个新的图形窗口,设置大小为8×6
# plt.plot(x, leaky_relu(x), label='leaky_relu alpha=0.01') # 绘制Leaky ReLU函数图像
# plt.plot(x, leak_relu_derivative(x), label='leak_relu_derivative alpha=0.01') # 绘制Leaky ReLU函数导数图像
# plt.title("leak_relu_derivative and leaky_relu alpha=0.01") # 设置图形的标题
# plt.legend()
# plt.grid(True)
# plt.show()# 6.创建一个包含两个子图的图形窗口
plt.figure(figsize=(15, 8))# 第一个子图:绘制ReLU和Leaky ReLU函数的图像
plt.subplot(1, 2, 1) # (行数, 列数, 位置索引):1行2列的第1个子图
plt.plot(x, relu(x), label="relu") # 绘制 ReLU函数的曲线
plt.plot(x, leaky_relu(x), label="leaky_relu alpha=0.01") # 绘制Leaky ReLU的曲线
plt.title("relu and leaky_relu alpha=0.01") # 设置图形的标题
plt.xlabel("Input Value") # 设置x轴标签:输入值
plt.legend() # 显示图例,位置自动选择最佳位置,图例内容来自上面两个plot语句的label参数
plt.grid(True) # 在图形上显示网格线,便于观察和读取数值# 第二个子图:绘制Leaky ReLU函数及其导数的图像
plt.subplot(1, 2, 2) # 1行2列的第2个子图
plt.plot(x, leaky_relu(x), label='leaky_relu alpha=0.01') # 绘制Leaky ReLU函数图像
plt.plot(x, leak_relu_derivative(x), label='leak_relu_derivative alpha=0.01') # 绘制Leaky ReLU函数导数图像
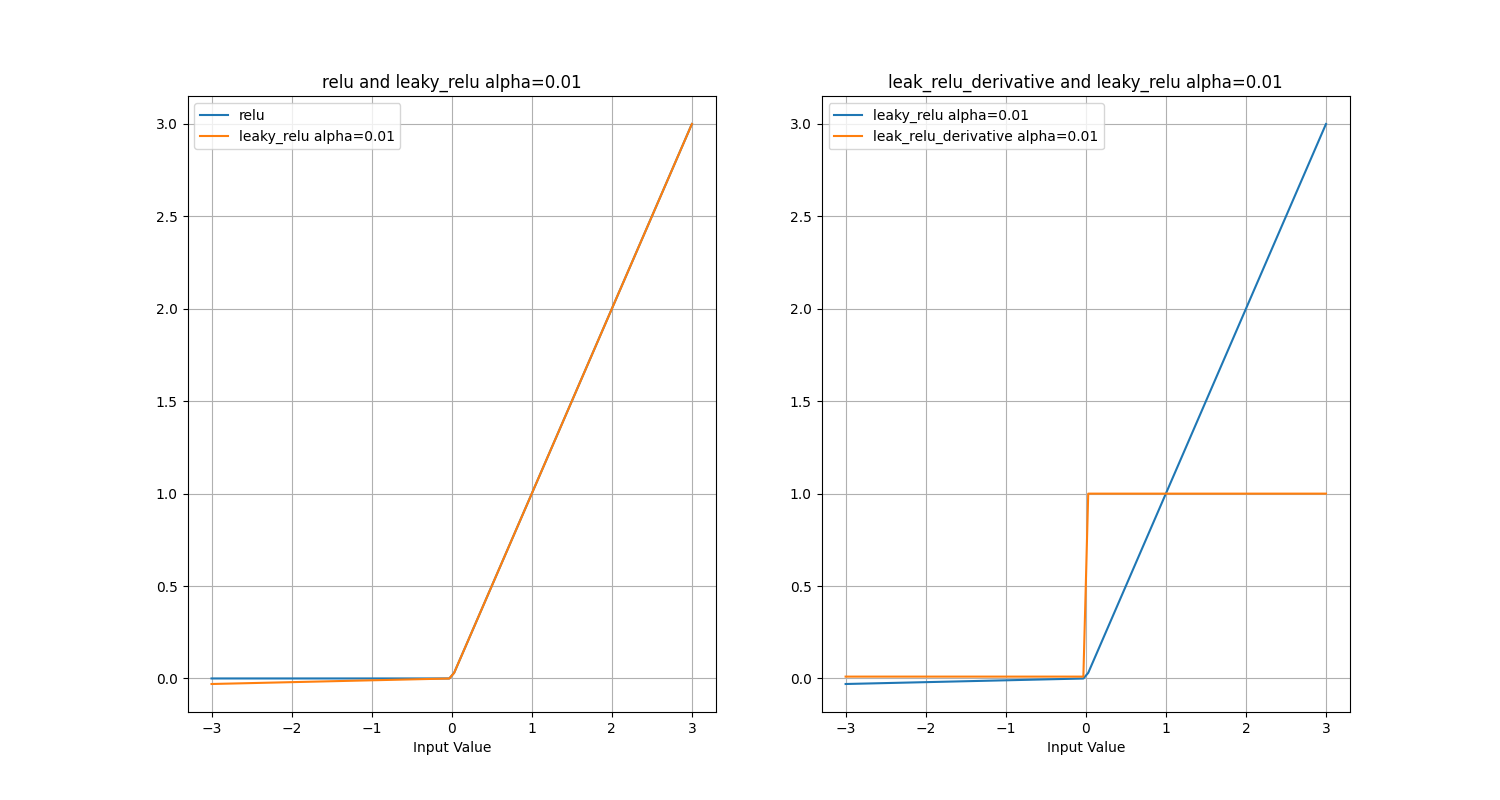
plt.title("leak_relu_derivative and leaky_relu alpha=0.01") # 设置图形的标题
plt.xlabel("Input Value") # 设置x轴标签:输入值
plt.legend()
plt.grid(True)
plt.savefig('Leaky ReLU.png')
plt.show()代码运行结果:Leak_ReLU.png
2.2.5 Prelu
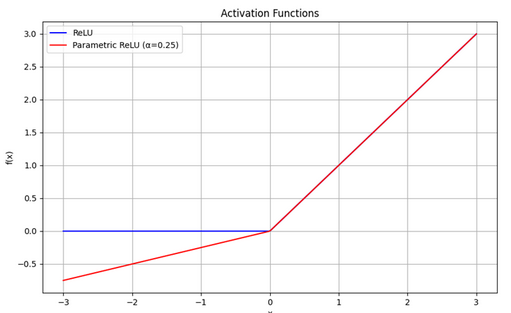
Prelu 和 Leaky Relu相比,Prelu的α是可学习的。
公式:f(x)=max(αx, x),其中 α 是一个可学习的参数。
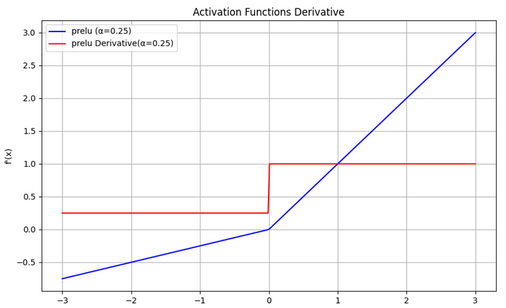
导数:
f’(x)=1,当x>0时。
f’(x)=α,当x<=0时。
PReLU是Leaky ReLu的一个变种,其中a是通过学习得到的,这使得模型可以适应性地改变其行为
# 1.导入必要的库
import numpy as np # 用于数值计算的库,提供了数组和矩阵操作等功能
import matplotlib.pyplot as plt # 用于绘图的库,可以绘制各种图表# 2.定义Parametric ReLU(PreLU)激活函数
def P_relu(x, alpha=0.25):return np.where(x > 0, x, x * alpha)"""
np.where(condition, x, y):当条件为真时返回x,否则返回y
当输入x>0时,返回x本身;否则返回x乘以alpha(默认0.25)
"""# 3.定义PReLU函数的导数
def P_relu_derivative(x, alpha=0.25):return np.where(x > 0, 1, alpha)"""
np.where(condition, x, y):当条件为真时返回x,否则返回y
代入代码中即是:当x>0时,导数为1;否则导数为alpha
"""# 4.创建输入数据
x = np.linspace(-3, 3, 100)
"""
创建从-3到3的等间距100个点的数组,作为函数的输入值
linspace(start, stop, num):生成指定范围内的等间隔数字
"""# 5.创建可视化图形
plt.figure(figsize=(8, 6)) # 创建一个8×6英寸的图形窗口
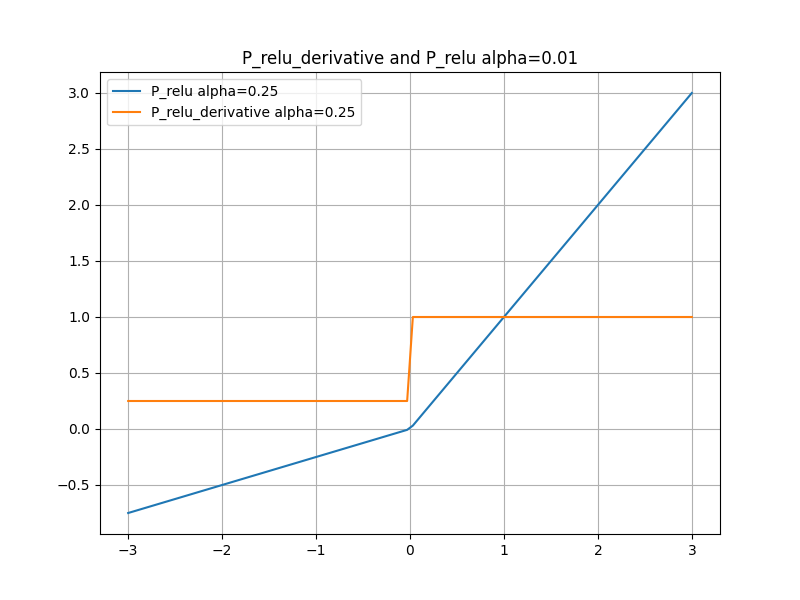
plt.plot(x, P_relu(x), label='P_relu alpha=0.25') # 绘制PReLU函数
plt.plot(x, P_relu_derivative(x), label="P_relu_derivative alpha=0.25") # 绘制PReLU函数的导数
plt.title("P_relu_derivative and P_relu alpha=0.01") # 设置标题
plt.legend() # 显示图例
plt.grid(True) # 添加网格线
plt.savefig('Prelu.png') # 保存图像
plt.show() # 显示图形代码运行结果:Prelu.png
2.2.6 ELU
ELU(Expoentital Linear Unit)激活函数是深度学习中用于增强网络学习能力的又一种激活函数,ELU通过在负值输入时提供负值输出,旨在结合Relu的优点和解决其潜在的一些问题,如ReLU的不活跃神经元问题。
数序定义
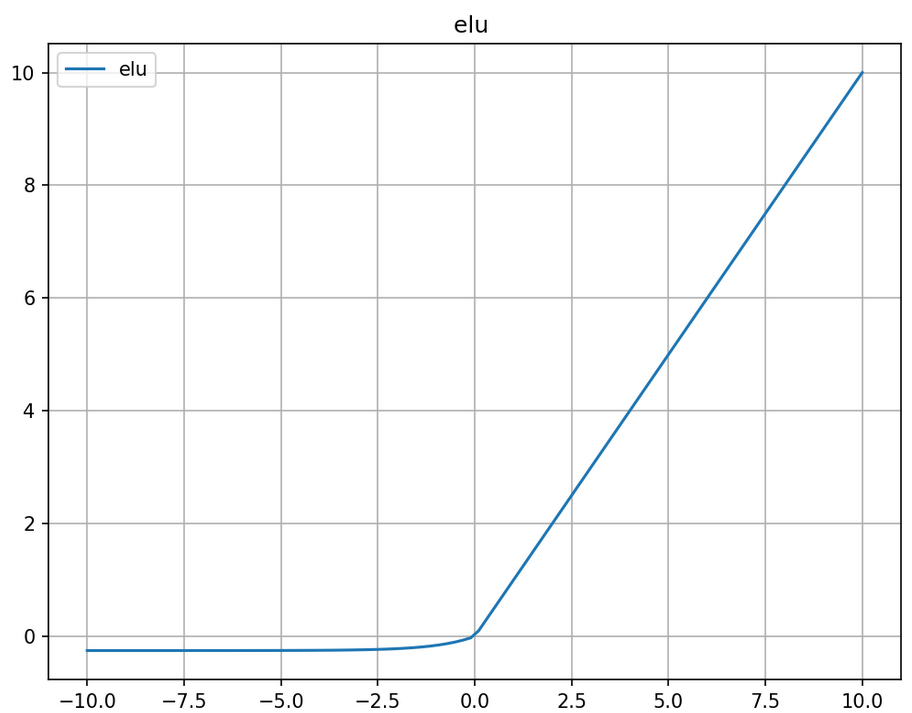
ELU函数的数学表达式定义为:
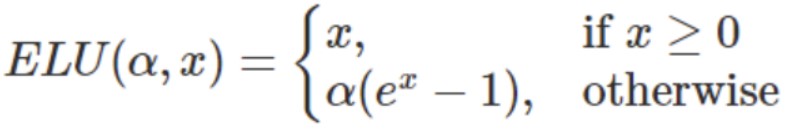
x是函数的输入,α是一个预定义的超参数,用于控制x为负值时输出的饱和度。
图像如下:
函数特性:
非线性:ELU是非线性的,可以帮助神经网络学习复杂的数据表示。
连续可导:ELU在整个定义域内连续可导,这有助于提高梯度下降优化算法的稳定性。
解决梯度消失问题:对于负值输入,ELU提供了负值输出,这有助于减轻梯度消失问题,尤其是在深度网络中。
输出均值接近0:ELU函数能够产生负值输出,这意味着其激活输出的均值更接近0,有助于数据的中心化,减少训练过程中的偏置偏移。
导数
ELU函数的导数: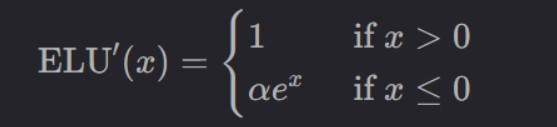
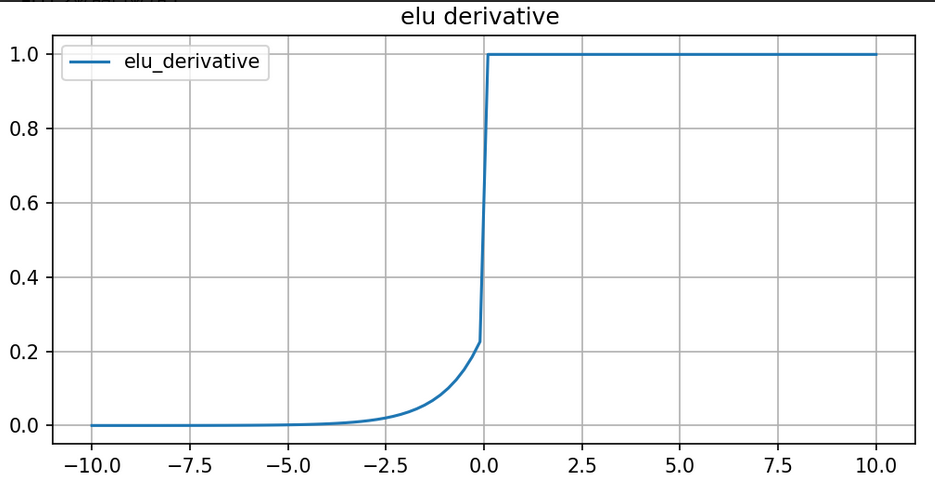
图像如下:
这意味着在正数区域,梯度为1,而在负数区域,梯度取决于α和x的指数值,这有助于保持负输入值的梯度更新。
ELU优势:
ELU通过在负数区域引入指数衰减,能够减少ReLU的“死亡”问题,同时保持负值的输出,有助于保持平均激活接近零,这有助于加快学习。
ELU劣势:
计算成本:由于ELU在负值时涉及指数运算,其计算成本高于Relu及其直接变体,尤其是在前向传播时。
# 1.导入必要的库
import numpy as np
import matplotlib.pyplot as plt# 2.定义ELU(Exponential Linear Unit)激活函数
def elu(x, alpha=0.25):return np.where(x > 0, x, alpha * (np.exp(x) - 1))"""当x > 0时,返回x本身当x ≤ 0时,返回α*(e^x - 1)
alpha参数控制负值区域的饱和点,默认为0.25
"""# 3.定义ELU函数的导数
def elu_derivative(x, alpha=0.25):return np.where(x > 0, 1, alpha * np.exp(x))"""
当x > 0时,导数为1
当x ≤ 0时,导数为α*e^x
"""# 4.创建输入数据
x = np.linspace(-10, 10, 100)
"""
创建一个包含100个点的数组,范围从-10到10
这些点将作为我们绘制函数的x坐标
"""# 5.计算每个x点对应的ELU函数值和导数值
y_elu = elu(x)
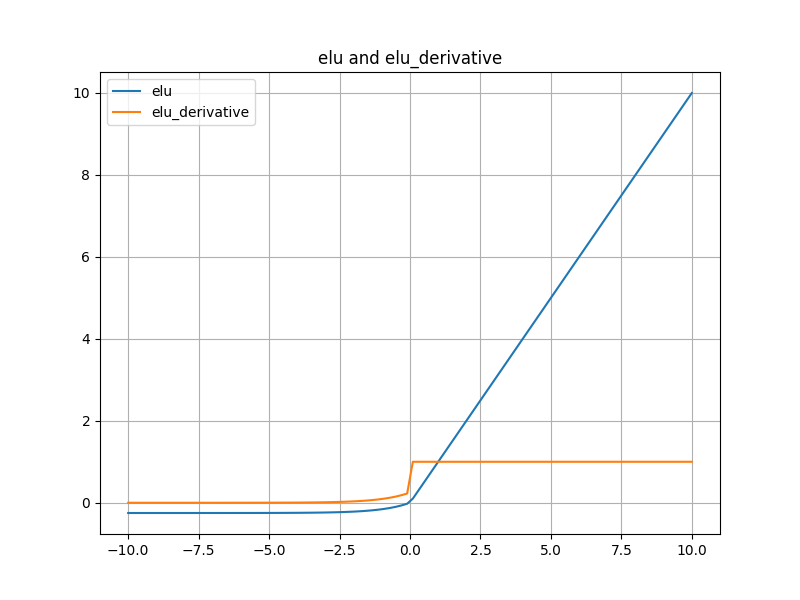
y_derivative = elu_derivative(x)# 6.绘制ELU函数图像
plt.figure(figsize=(8, 6)) # 创建一个新的图形窗口,设置大小为8×6英寸
plt.plot(x, y_elu, label='elu') # 创建ELU函数图像,
plt.plot(x, y_derivative, label='elu_derivative') # 创建ELU导数图像
"""label参数为图例提供标签文本"""
plt.title('elu and elu_derivative') # 设置图表标题
plt.legend() # 显示图例,标识每条曲线代表的函数
plt.grid(True) # 显示网格线,便于读取坐标值
plt.savefig('ELU.png')
plt.show() # 显示图形窗口代码运行结果:ELU.png
2.2.7 Softmax
softmax激活函数,但是很多地方,不会把softmax称为激活函数,但是呢没有一个合理的叫法,它就叫softmax函数,但是呢,它的性质上无论和我们的sigmoid或者tanh 或者relu等其实是类似的,我们可以把它称为激活函数。
softmax激活函数为什么不把它称为激活函数,是因为和它的位置是有关系的。为什么呢?
softmax这个函数和我们的sigmoid函数也好。relu函数也好,不一样的点在哪里?sigmoid函数一般位于算法的最后一层,softmax函数它一般只用于最后一次的激活,也就是输出之前的一次激活,前面不用softmax。 softmax一般不用于回归算法中,一般是用于分类中,我们前面计算的都是在算拟合和回归,softmax它做的是分类。
eg:猫和狗,当我们的输出不是一个值而是一个向量的时候,比如要分成三类(猫,狗 ,老虎)三类,根据输出的向量数值,按照下面的公式进行计算。
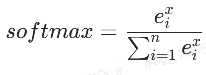
然后再计算后然后再计算损失函数。
Softmax函数,可以将神经网络计算出来的数值通过公式变成概率,经过softmax后得到的结果相加和为1。
另一个优势就是不论向量输出的结果是正值还是负值都能转化为正值。
这个在后续的深度学习中用的非常多。
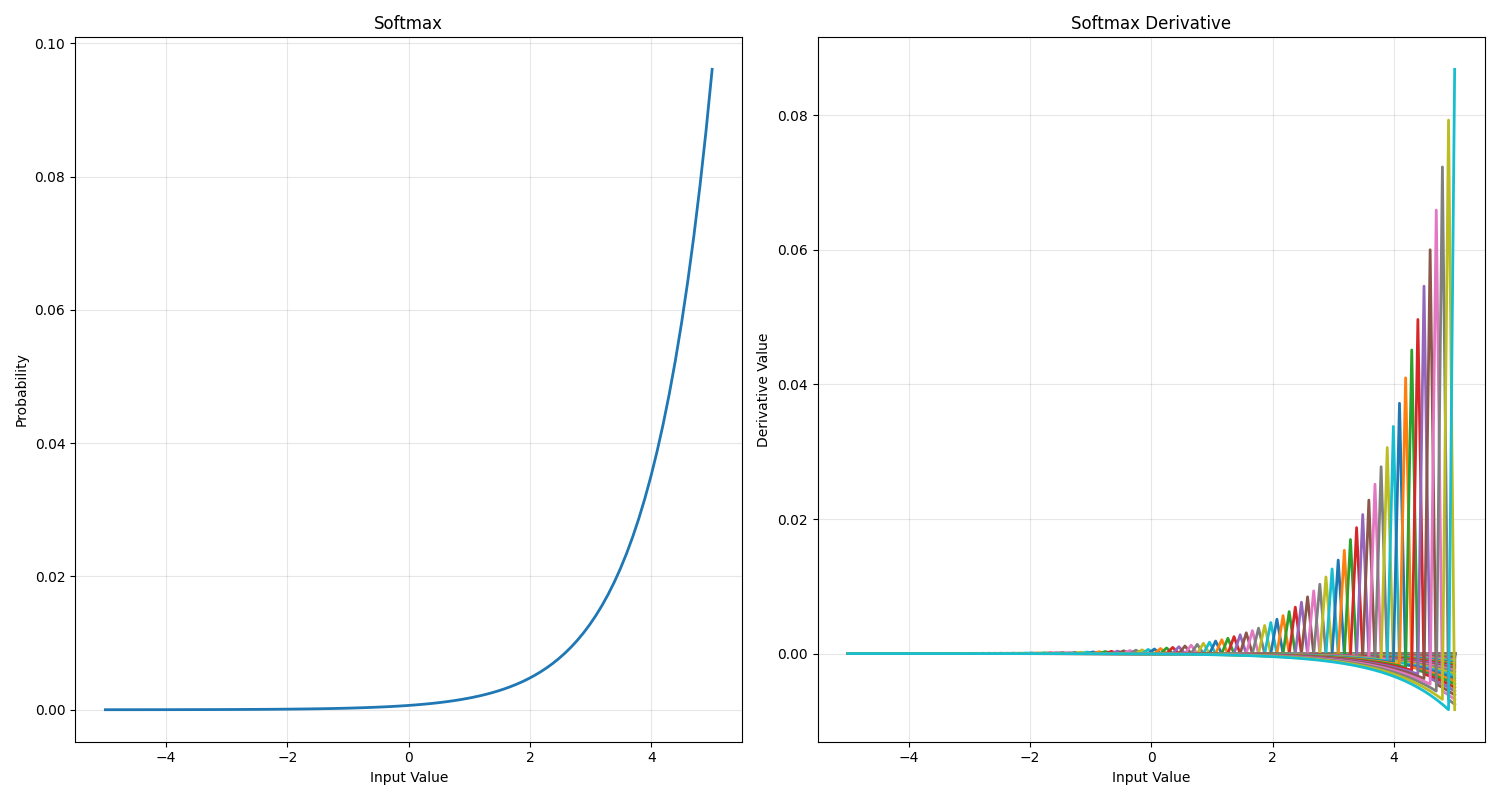
当n=100时,即有100类时,其图像如下图所示:
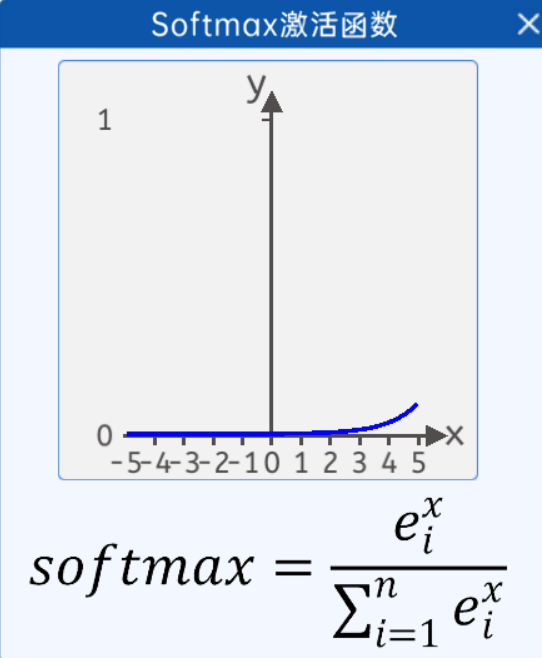
softmax 特点总结:
概率分布:Softmax函数将输入转换为概率分布,因此在多分类问题中常用于将模型的原始输出转换为概率值。
连续可导:Softmax函数是连续可导的,这使得它可以与梯度下降等优化算法一起使用进行训练。
指数增长:Softmax函数中的指数运算可能会导致数值稳定性问题,特别是当输入较大时。为了解决这个问题,可以通过减去输入向量总的最大值来进行数值稳定的计算。
梯度计算简单:Softmax函数的导数计算相对简单,可以通过对Softmax函数的定义进行微分得到。
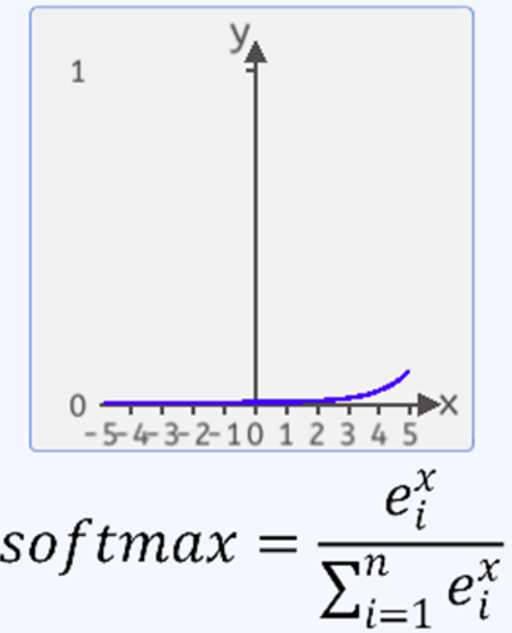
求导:



# 1.导入必要的库
import numpy as np # 用于数值计算的库,提供了数组和矩阵操作等功能
import matplotlib.pyplot as plt # 用于绘图的库,可以绘制各种图表# 2.定义softmax函数
def softmax(x):vals = np.exp(x)return vals / np.sum(vals)"""np.exp(x)计算输入数组x中每个元素的指数函数值(e^x)np.sum(vals)计算所有指数值的总和最后将每个指数值除以总和,得到概率分布(所有输出值之和为1)Softmax函数常用于多分类问题的输出层,将任意实数值转换为概率分布
"""# 3.计算softmax函数的导数
def softmax_derivative(x):s = softmax(x)return np.diagflat(s) - np.outer(s, s)"""首先计算输入x的softmax值snp.diagflat(s)创建一个对角矩阵,对角线元素为s的值np.outer(s, s)计算向量s的外积(s·s^T)softmax的导数公式为:∂s_i/∂x_j = s_i(δ_ij - s_j),其中δ_ij是Kronecker delta函数(i=j时为1,否则为0)这个公式可以表示为矩阵形式:diag(s) - s·s^T
"""# 4.创建输入数据
x = np.linspace(-5, 5, 100)
"""np.linspace(-5, 5, 100)在-5到5之间生成100个等间距的点这些点将作为softmax函数及其导数的输入
"""# 5.计算每个x点对应的softmax函数值和导数值
y_softmax = softmax(x) # 存储softmax函数在x各点处的值
y_derivative = softmax_derivative(x) # 存储softmax函数在x各点处的导数值# # 6.绘制softmax函数图像
# plt.figure(figsize=(10, 6)) # 创建一个10×6英寸的图形窗口
# plt.plot(x, y_softmax) # 绘制x和y_softmax的曲线
# plt.title("softmax") # 设置图形标题
#
# # 7.绘制softmax导数图像并显示
# plt.figure(figsize=(10, 6))
# plt.plot(x, y_derivative) # 绘制softmax导数图像
# plt.title("softmax derivative")# 6.创建一个包含两个子图的图形窗口
plt.figure(figsize=(15, 8)) # 创建一个宽度能容纳两个子图的窗口# 第一个子图:Softmax函数
plt.subplot(1, 2, 1) # (行数, 列数, 位置索引):1行2列的第1个子图
plt.plot(x, y_softmax, linewidth=2)
"""x: x轴数据(输入值)y_softmax: y轴数据(Softmax输出值)linewidth=2: 线条宽度为2像素
"""
plt.title("Softmax") # 设置子图标题
plt.xlabel("Input Value") # 设置x轴标签:输入值
plt.ylabel("Probability") # 设置y轴标签:概率
plt.grid(True, alpha=0.3) # 添加网格线
"""alpha=0.3: 设置网格线透明度为30%"""# 第二个子图:Softmax导数
plt.subplot(1, 2, 2) # 1行2列的第2个子图
plt.plot(x, y_derivative, linewidth=2)
plt.title("Softmax Derivative") # 设置子图标题
plt.xlabel("Input Value") # 设置x轴标签:输入值
plt.ylabel("Derivative Value") # 设置y轴标签:导数值
plt.grid(True, alpha=0.3)# 调整子图间距
plt.tight_layout() # 自动调整子图参数,使它们不会重叠# 保存图像
plt.savefig('softmax_and_derivative.png')plt.show() # 显示所有图形"""
梯度在机器学习中的应用优化算法:梯度下降法使用负梯度方向来更新参数,以最小化损失函数反向传播:在神经网络中,梯度用于计算损失函数对网络参数的偏导数特征重要性:梯度大小可以指示输入特征对输出的影响程度
"""代码运行结果:softmax_and_derivative.png