当前位置：首页 > news >正文

永磁同步电机 FOC 控制中 d、q 轴杂谈与角度偏移影响

news 2025/9/7 7:08:00

一、基本公式概念

1.1 Clark 和 Park 变换公式

1.1.1 Clark 变换公式

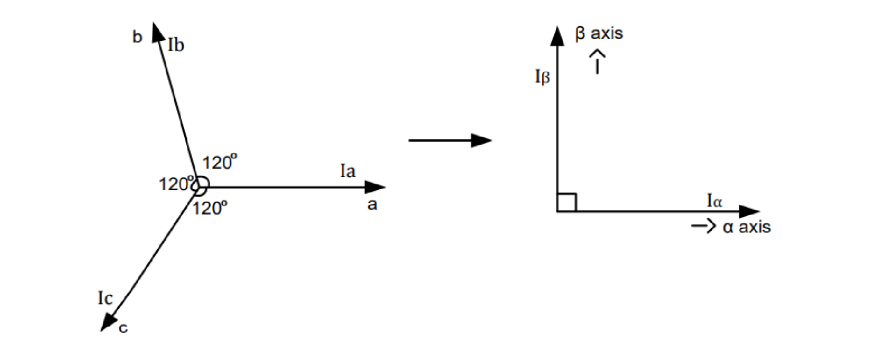
Clark 变化就是把三项电压矢量 (a、b、c) 的 120° 的电流分量，转化为两轴 (α、β) 90° 的电流分量。

这种变换的物理意义是：用两个正交分布的虚拟线圈（α 轴和 β 轴）模拟三相电机中 120° 分布的三个实际线圈的磁场效果。数学上，这种等效性保证了磁场合成的效果一致。

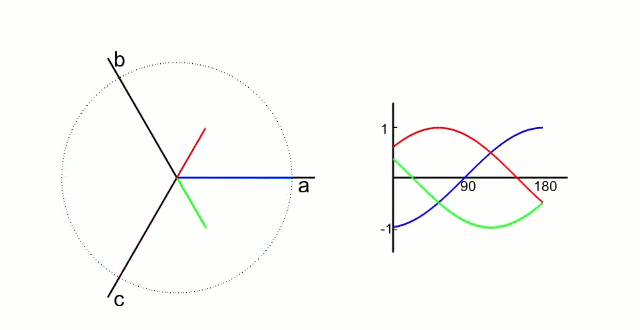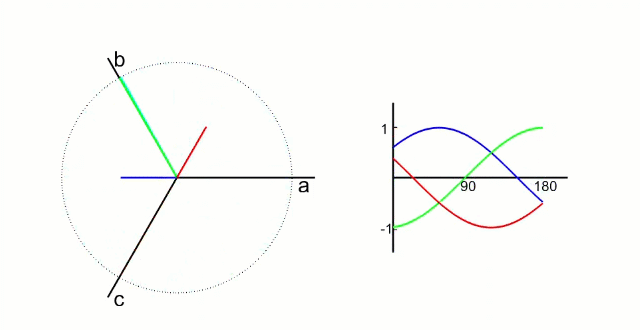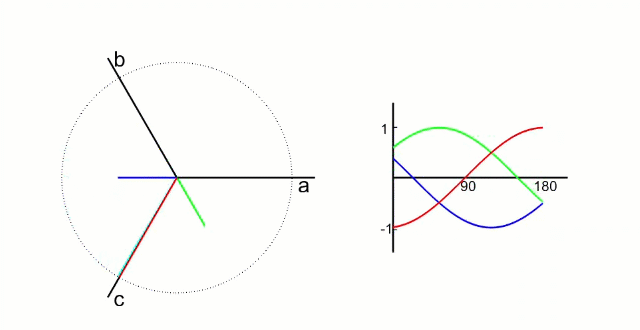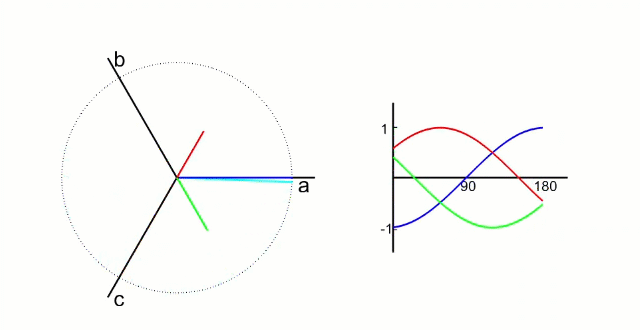
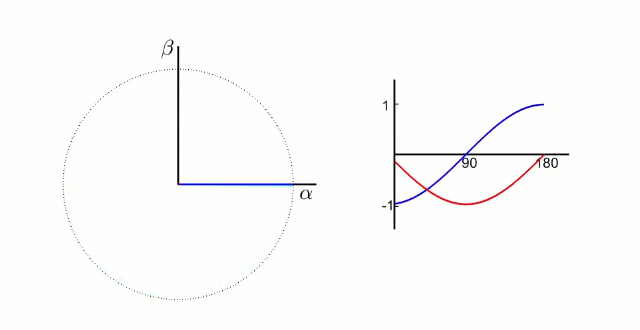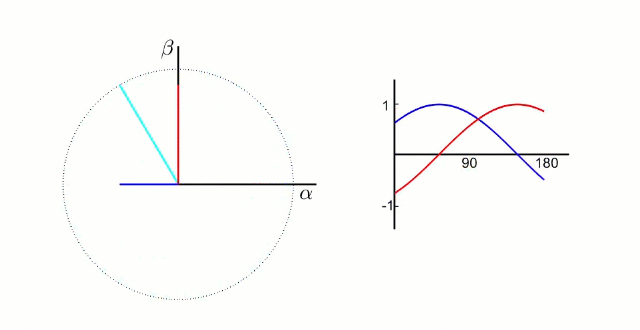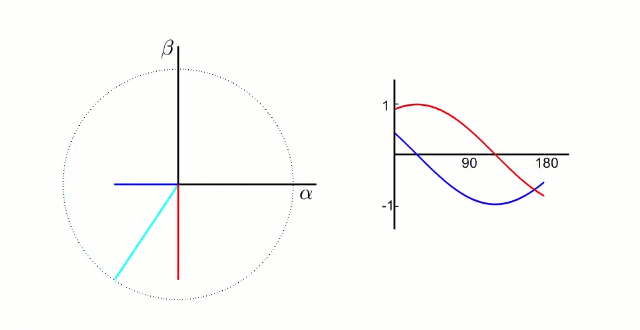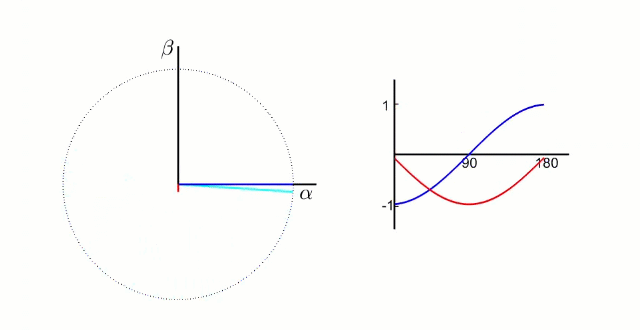
1.1.2 Park 变换

Clark 变化得到的 α、β 包括当前转子角度信息 θ。Park 变换后将 α、β 中的角度信息剔除即可得到 q、d 轴的值。

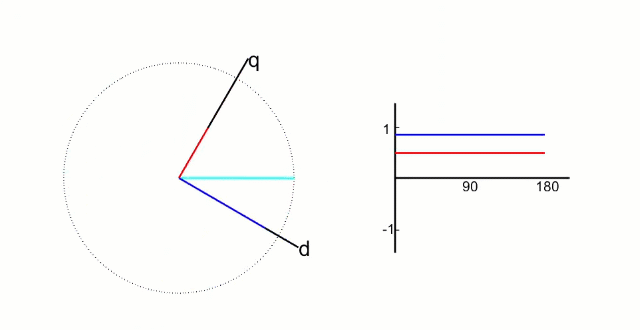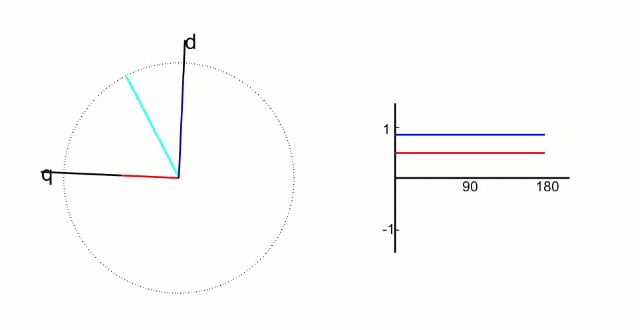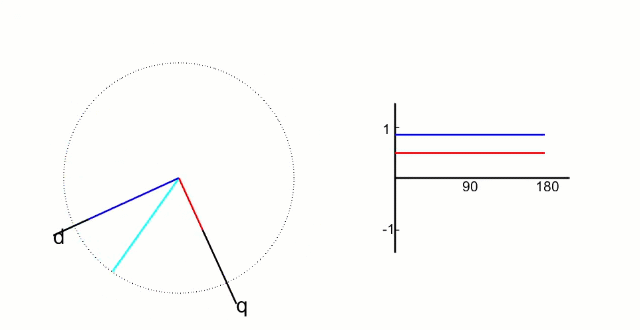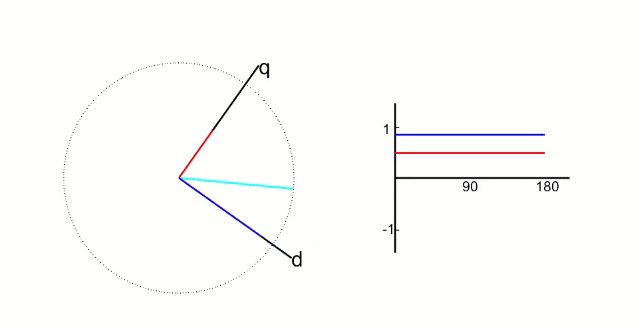
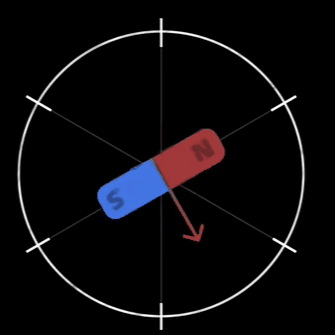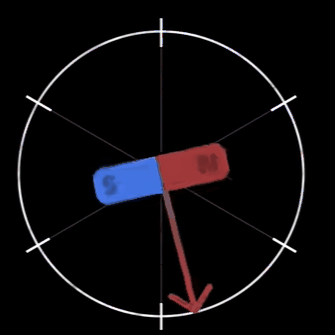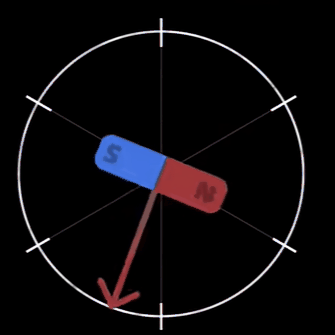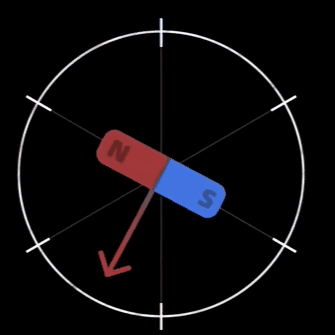
d 轴：(direct-axis) 与转子磁场方向重合，即沿转子磁极的中心线方向 (从 S 极指向 N 极) 。在永磁同步电机中，d 轴通常用于控制磁场的励磁分量。
q 轴：垂直于转子磁场方向，即位于相邻磁极的垂直平分线上。其名称来源于 “quadrature” (正交)，表示与 d 轴的电角度相差 90°。

简单来说，d 轴和转子 N 极磁铁方向重合，代表磁通分量；而 q 轴正交于 d 轴，和磁通无关只控制力矩。

1.2 id、iq 磁链公式

1.2.1 磁链

磁链（Magnetic Flux Linkage）表示穿过导电线圈的总磁通量，在电路中，磁链与电流（I）通过电感（L）关联：

$\psi =L\cdot I$

$L$ = 电感值
$I$ = 电流值

1.2.2 三项磁链方程

$\psi _{a}$ 、 $\psi _{b}$ 、 $\psi _{c}$ = 转子永磁体磁链常数
$L_{aa}$ 、 $L_{bb}$ 、 $L_{aa}$ = 各自绕组的自感
$M_{ab}$ 、 $M_{ac}$ 、 $M_{bc}$ = 相间互感，对称系统中 $M_{bc} = M_{ba}$
$i_{a}$ 、 $i_{b}$ 、 $i_{c}$ = 三项定子电流
$\psi _{f}$ = 永磁体磁链幅值 (常数)
$\theta _{e}$ = 转子 d 轴与 A 相绕组的电角度

对于 B、C 相的反电动势和角度的关系正好是相差 120°，所以上述公式需要减去和加上 $\frac{2\pi }{3}$ 。

1.2.3 d、q 轴下的磁链方程

三项磁链方程太过于复杂，我们不考虑自感和互感等因素，并且将这个公式转化为 d、q 轴下的方程。因为 d、q 轴剔除了角度参数，所以 d、q 的下的磁链方程很简单。

$\begin{cases} \psi_d = L_d i_d + \psi_f \\ \psi_q = L_q i_q \end{cases}$

$L_{dq}$ = d、q 轴电感
$i_{dq}$ = d、q 轴电感
$\psi _{f}$ = 永磁体磁链幅值 (常数)

2.1 转矩方程

电机的转矩方程如下：

$T_{e}=\frac{3}{2}p_{n}i_{q}[i_{d}(L_{d}-L_{q})+\psi _{f}]$

$L_{d}$ = d 轴电感
$L_{q}$ = q 轴电感
$\psi_{f}$ = 磁链常数
$P_{n}$ = 极对数
$T_{e}$ = 电机转矩

对于表贴式电机 (SPMSM)，因为它的 d、q 轴电感几乎相等，所以转矩公式被简化成了这样：

$T_e = \frac{3}{2} p_{n} \psi_f i_q$

$\psi_{f}$ = 磁链常数
$P_{n}$ = 极对数
$T_{e}$ = 电机转矩

二、为什么 id 代表磁链，而 iq 代表力矩

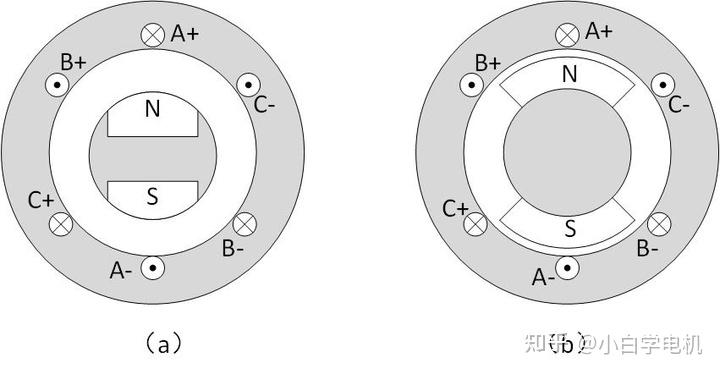
永磁体磁导率相当于空气，而铁的导磁率约为 200~400 Ur 。对于表贴式电机来说，它的 d 轴方向和 q 轴方向用铁量一样多，所以 d 轴和 q 轴的电感相等。

为了简化这个 id 和 iq 分量的问题，下文仅使 d、q 轴电感相等的表贴式电机分析。

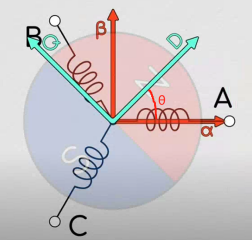
d 轴是与转子磁场对齐的轴（d轴和转子磁铁正极方向相同），它代表了电机中的磁链的主要方向。在电机中，尤其是同步电机（如永磁同步电机、异步电机等），磁链的大小和方向决定了电机的磁耦合程度。

q 轴与 d 轴垂直，它代表了与转矩产生相关的部分。在 d-q 轴坐标系中，q 轴电流与电机的转矩密切相关。转矩是由定子电流与转子磁场的相对运动产生的，q 轴电流与转矩的产生有直接关系。

那么，我们在讨论磁链公式时，q 轴同样拥有单独的磁链值，这是怎么回事呢？

$\begin{cases} \psi_d = L_d i_d + \psi_f \\ \psi_q = L_q i_q \end{cases}$

$L_{dq}$ = d、q 轴电感
$i_{dq}$ = d、q 轴电感
$\psi _{f}$ = 永磁体磁链幅值 (常数)

对于 id、iq，他们相差 90°，所谓 q、d 轴磁链就是在这两个角度下对转子的磁力强度。如果我们将磁通完美的施加到 d 轴上，这样转子是不会旋转的。只有施加到 q 轴上才能像胡萝卜一样牵引转子旋转，这也是因为表贴式电机保持 id=0 的控制的原因。

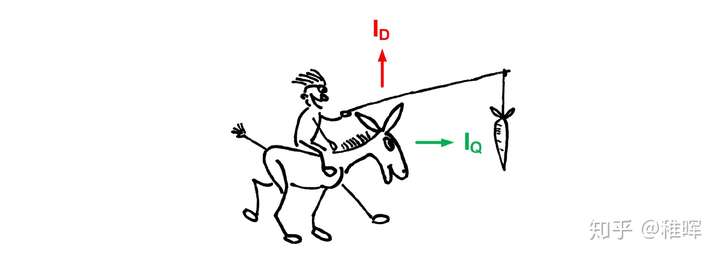
而我们根据表贴式电机 (Ld≈Lq) 力矩公式可得：

$T_e = \frac{3}{2} p_{n} \psi_f i_q$

$\psi_{f}$ = 磁链常数
$P_{n}$ = 极对数
$T_{e}$ = 电机转矩

因此，转矩仅由交轴电流 iq 决定，与直轴电流 id 无关。

表贴式PMSM通常采用 id = 0 控制策略，以最大化单位电流下的转矩输出。

三、弱磁控制原理

3.1 弱磁概述

电机的转速上限，往往受直流母线电压限制。

在中低速时，电机产生的反电动势 (Back EMF) 还小，控制器能轻松加电流、加电压来驱动电机。但是当转速高了以后，电机定子绕组产生的反电动势会增大，接近甚至超过母线电压：

$E=\omega \cdot \psi _{f}$

$E$ = 反电动势
$\omega$ = 电机角速度
$\psi _{f}$ = 转子永磁体的磁链

弱磁的核心思想就是人为减小电机的等效磁链 $\psi$ ，从而降低反电动势 $E$ ，让电机还能继续加速。

在 $d$ 轴上注入一个负的 $i_{d}$ 电流，这样在公式上就反应为：

$\psi_d = L_d i_d+ \psi_f$

$L_{d}$ = d、q 轴电感
$i_{d}$ = d、q 轴电感
$\psi _{f}$ = 永磁体磁链幅值 (常数)

根据此公式当 $i_{d}<0$ 时， $\psi_d$ 变小，进而产生：

有效磁链减小 ⇒ 反电动势减小 ⇒ 需要的电压减小 ⇒ 电机还能继续提升转速。

3.2 弱磁的代价

根据电机力矩公式

$T_e = \frac{3}{2} p_{n} \psi_f i_q$

$\psi_{f}$ = 磁链常数
$P_{n}$ = 极对数
$T_{e}$ = 电机转矩

削弱了磁链常数后，磁链变小，转矩能力变小，为了维持转矩，就需要更大的 $i_{q}$ 。

高速弱磁区，电机效率一般比低速恒功率区低。

如下图所示，如果我们的 $i_{d}$ 弱磁后在 C 点，那么 $i_{q}$ 只能在 A 点才能保持较大的效率。

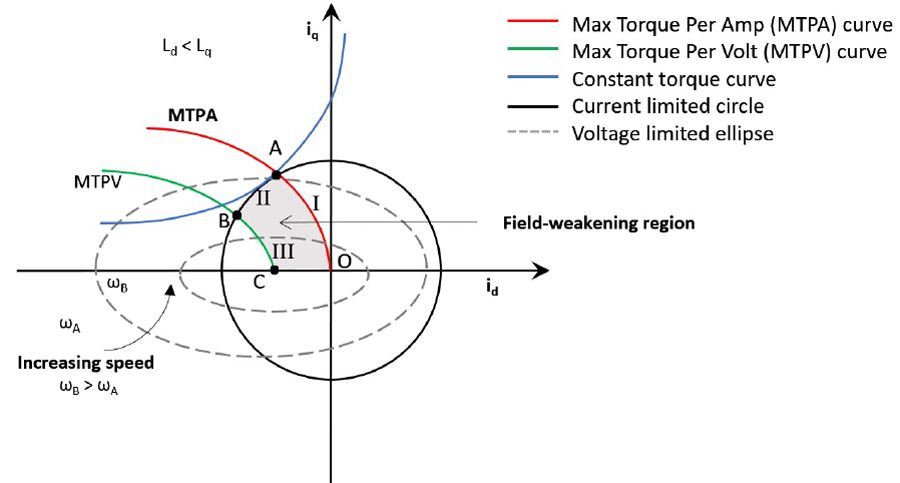
弱磁控制就是通过在 d 轴注入负电流抵消部分磁链，降低反电动势，从而突破电压限制，让电机在额定转速以上还能继续高速运行，但转矩会下降。

四、控制角度偏移对 id、iq 的影响

请注意，FOC 控制中的角度指的是 d 轴的角度，q 轴角度要比 d 轴小 90°。

4.1 电流环开环情况

我们将 d、q 轴电流用 RTT 打印出来后就赋值成 0，这样对于 FOC 框架来说，d、q 轴就一直是 0，相当于是电流环在开环跑。

FOC 框架会将 d 轴 0 输出 (因为我们是 id = 0 目标控制，当前反馈被强制设为 0，所以自然就是 0 输出了)，q 轴的 pi 调节因为反馈一直是 0，但是目标值却不是 0，所以 q 轴输出会最大。

Rttstru.data0 = t_Park_CurRegS.s32_Qs;
Rttstru.data1 = t_Park_CurRegS.s32_Ds;
SEGGER_RTT_Write(1, &Rttstru, 8);t_Park_CurRegS.s32_Qs = 0;
t_Park_CurRegS.s32_Ds = 0;

在在下图中：

rtt_channel1.data0	q 轴电流 (红色)
rtt_channel1.data1	d 轴电流 (绿色)
bus_cur	母线电流 (单位 A)
speed.SpeedRpm	转速 (单位Rpm)
theta_offset	角度偏移 (可调节值)

4.1.1 不偏移角度情况

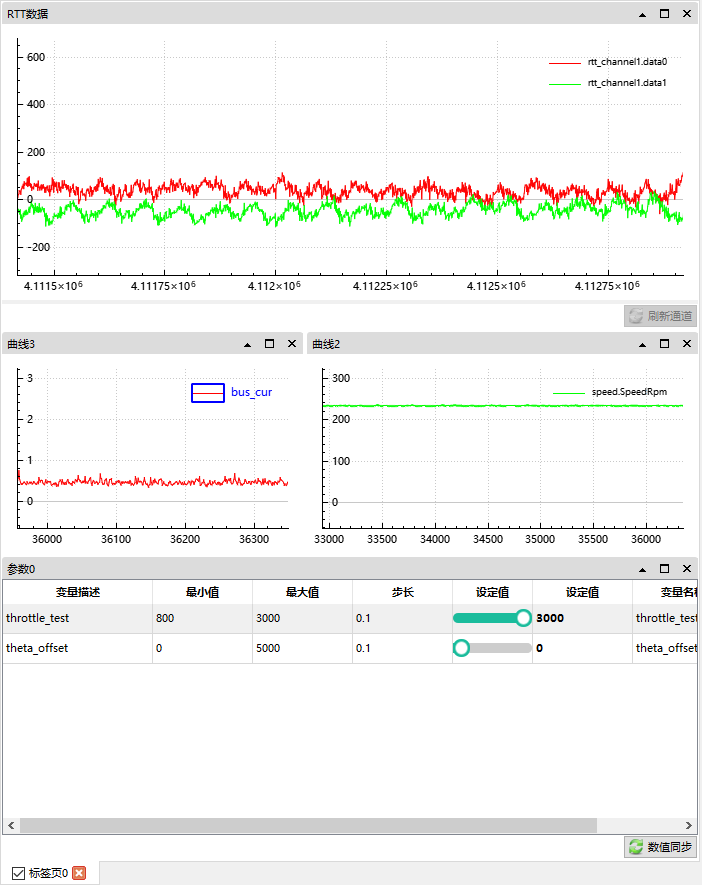
根据图片可观察到：

此时电机空转无负载。
我们可以观察到当前 q 轴电流略高于 d 轴；
母线电流 0.5A；
电机转速在 230 Rpm；
角度偏移为 0；

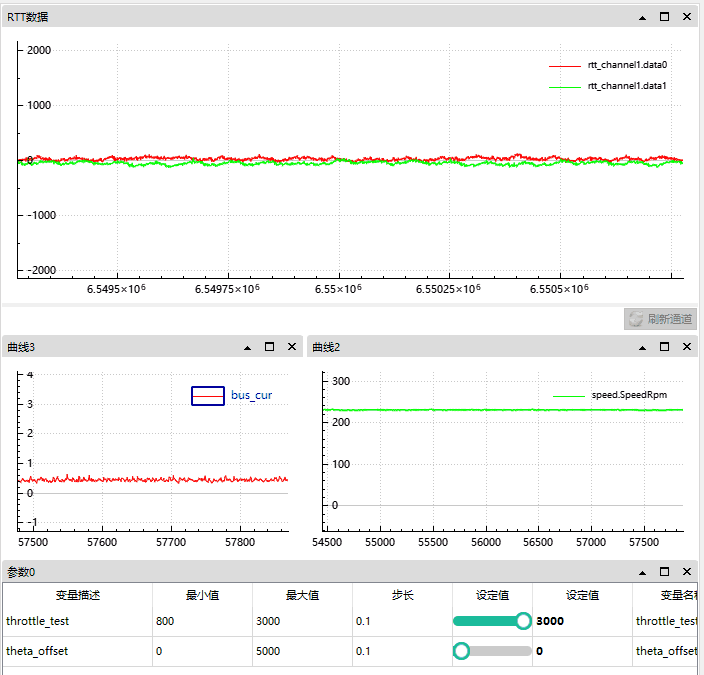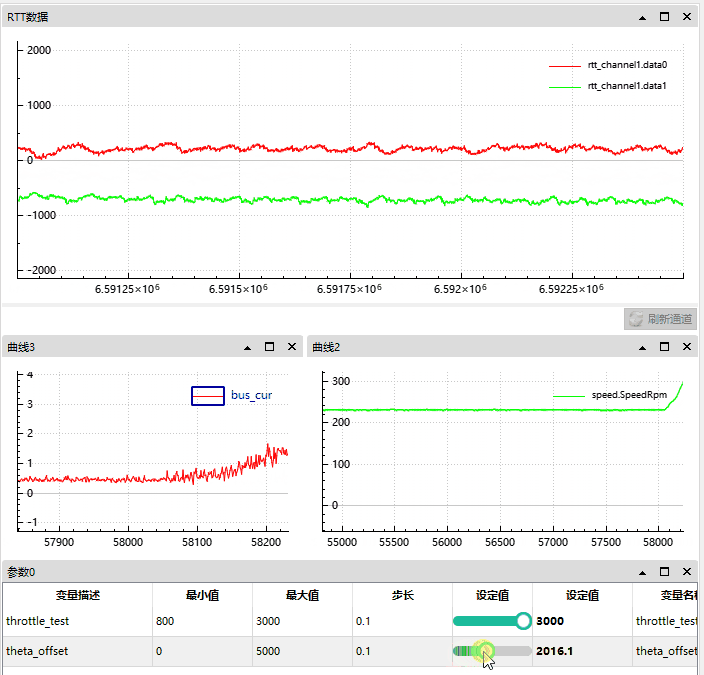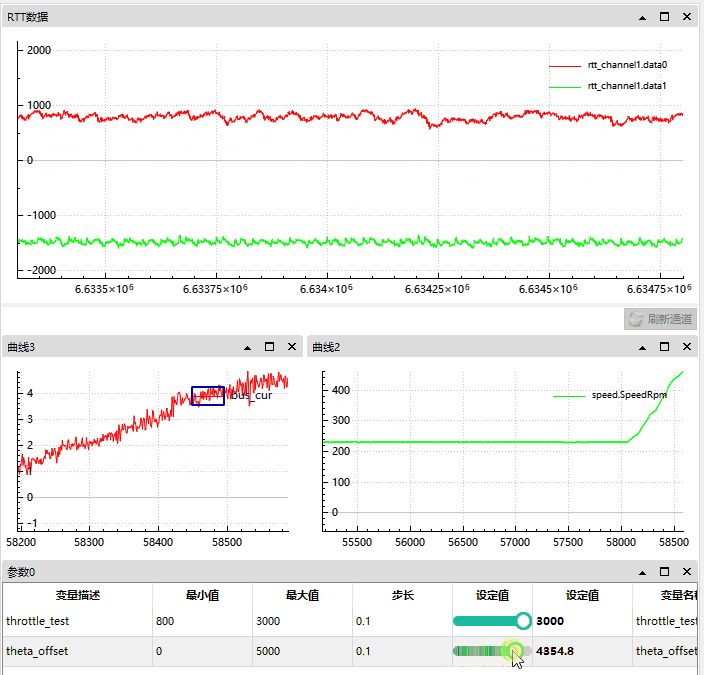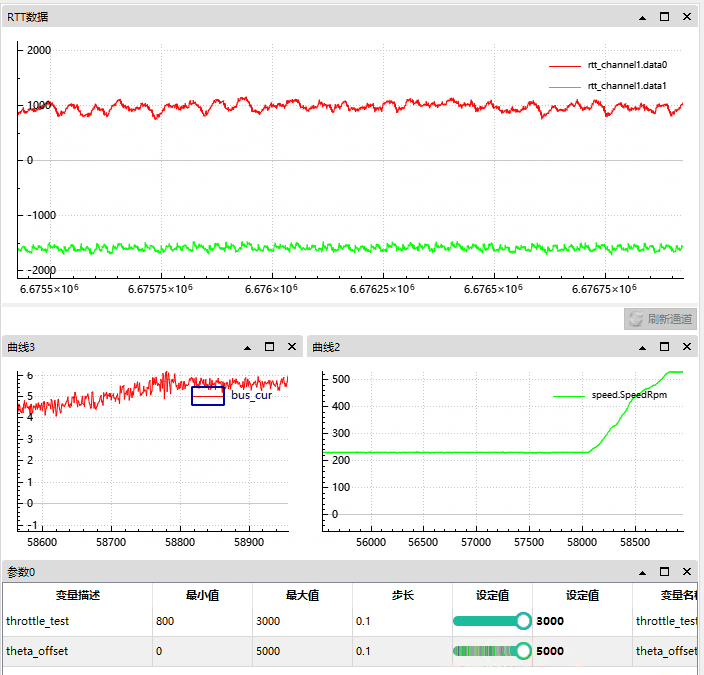
4.1.2 角度正向偏移情况

我们将角度从 0 偏移增至 5000 时，d 轴被自然削弱 (因为此时 q 轴产生了向 d 轴的偏差，d 和 q的偏差将小于 90°)。

根据 gif 图可知：

正向偏差角度越大， d 轴反馈越小；
母线电流从 0.5A 升到了 5A，
速度从 230 Rpm 升到了 500；

我们可以近似的看作当时电机通过偏移角度实现了弱磁。

4.1.3 角度反向偏移情况

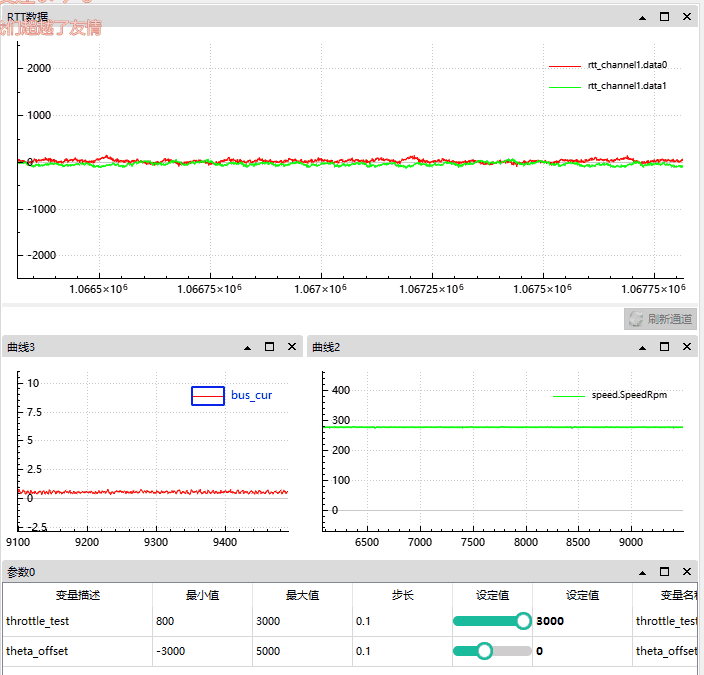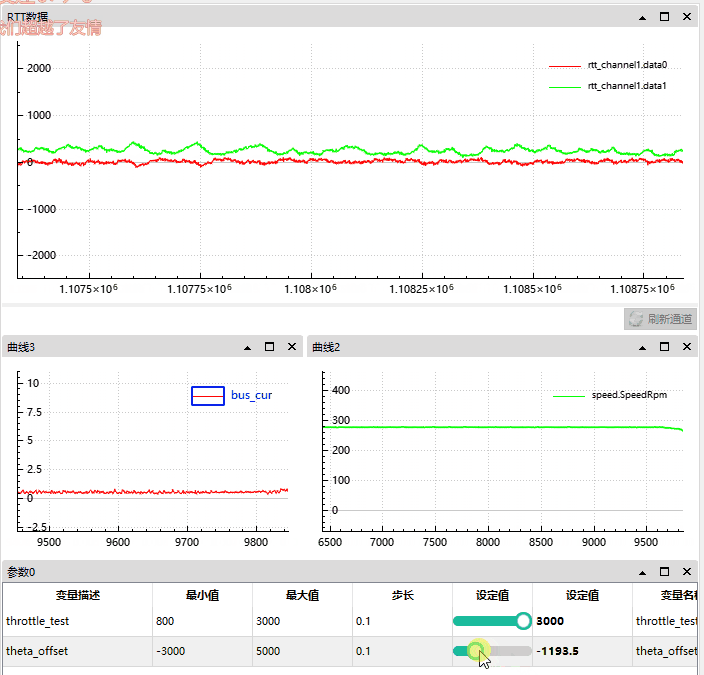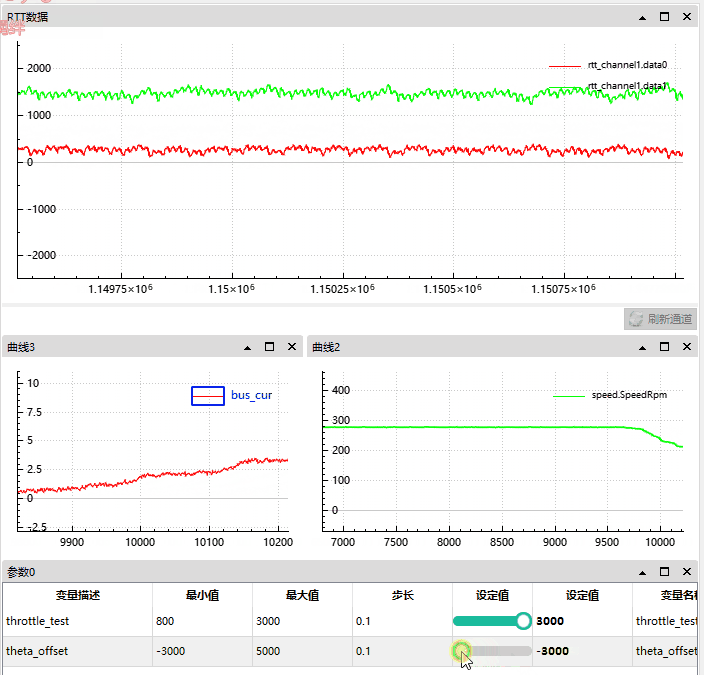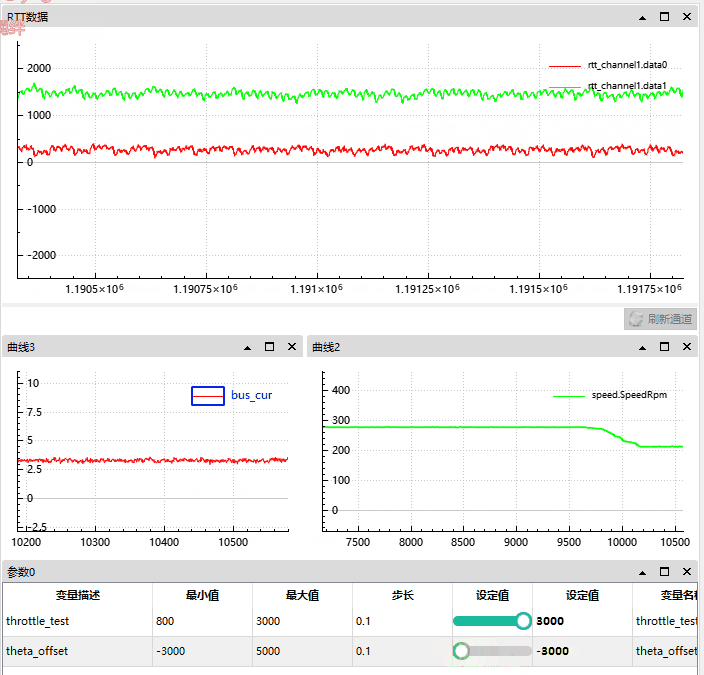
我们将角度从 0 偏移增至 -3000 时，d 轴被自然增大 (因为此时 q 轴产生了向 d 轴的偏差，d 和 q的偏差将小于 90°)。

根据 gif 图可知：

反向偏差角度越大， d 轴反馈越大；
母线电流从 0.5A 升到了 3A；
速度从 230 Rpm 降低到了 200；

我们可以近似的看作当时电机通过偏移角度实现了增磁，这样可以增加电机的力矩。

4.2 电流环闭环情况

在下面的实例中加入了电流闭环，此时就是正常的电机控制流程了。

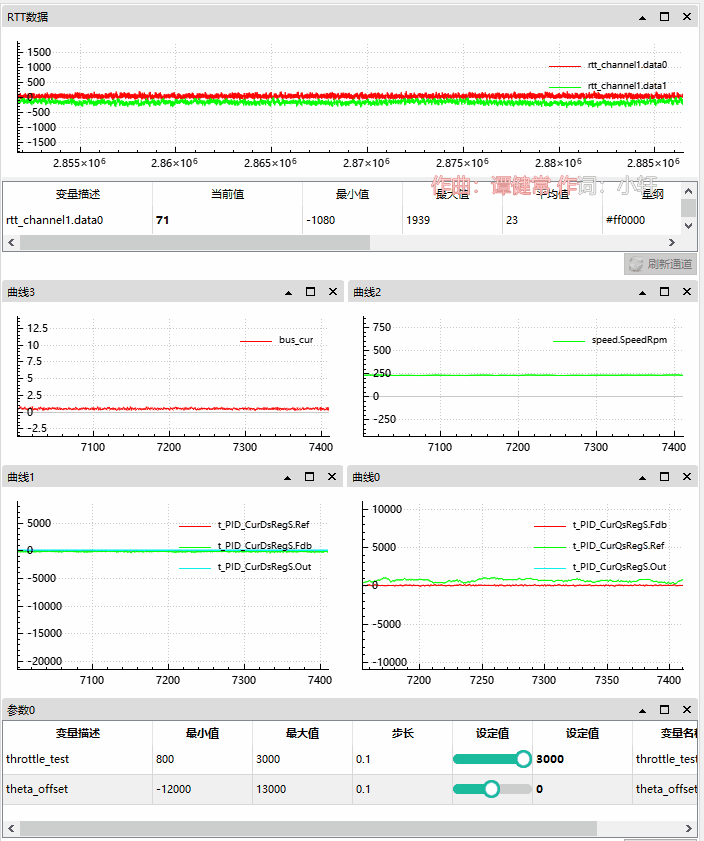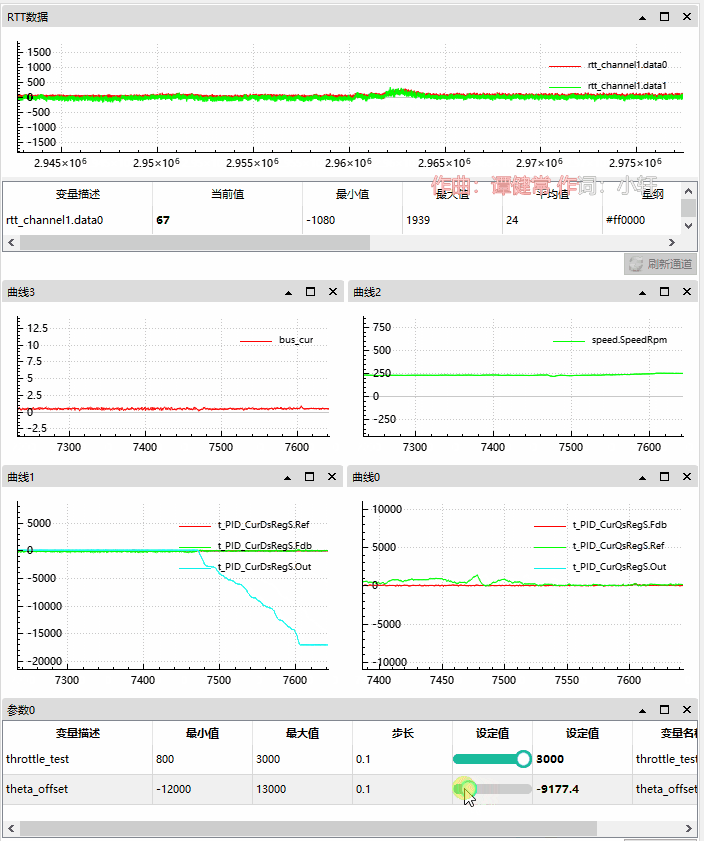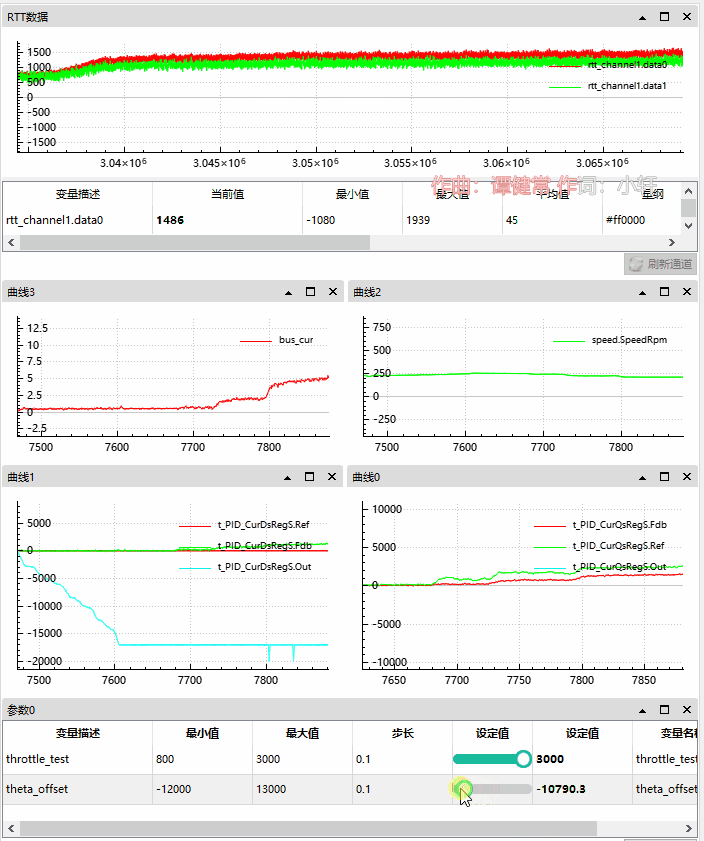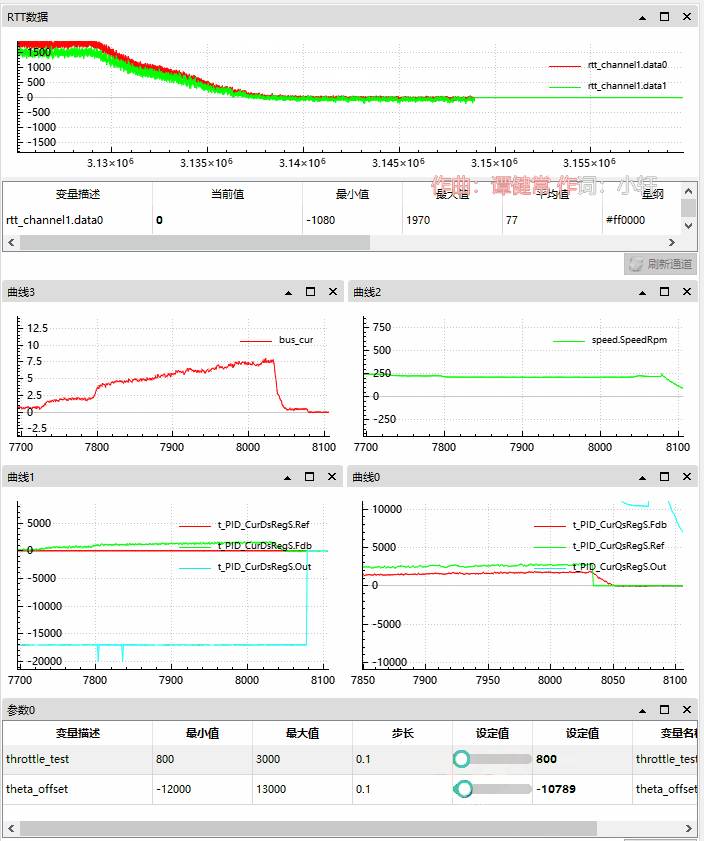
4.2.1 不偏移角度情况

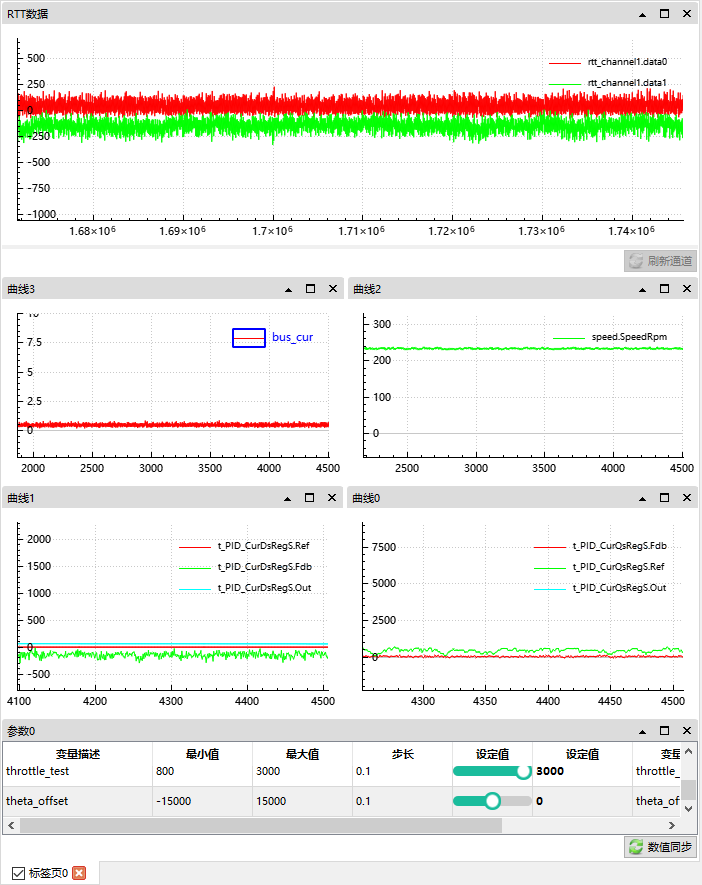
按这个案例中我们比之前的调试加入了 d 轴和 q 轴的 PI 反馈、目标和输出。

此时电机空转无负载。
我们可以观察到当前 q 轴电流略高于 d 轴；
母线电流 0.5A；
电机转速在 230 Rpm；
角度偏移为 0；
d 轴目标为 0，反馈为负 -200 左右，输出为 50；
q 轴目标为 500 左右，反馈为 50左右，输出为 20000；

4.2.2 角度正向偏移情况

此时电机空转无负载。
我们可以观察到正向偏移越大，q 轴偏移越大，d 轴少量的缩小。
母线电流从 0.5A 升至 4A；
电机转速在 230 Rpm 后轻微上升；
角度偏移从 0 至 13000；
d 轴目标为 0，反馈为负 -200 左右至 -1000 左右，输出逐渐增大，直到 10000 最大值；
q 轴目标为 2000 左右，反馈为 1000 左右有减小趋势，输出开始最大 20000，后逐渐减小；

由以上观察可以得到结论，如果在电流闭环的情况下，输入角度与实际值有偏差会导致 d 轴产生偏差，但是我们仍以 id = 0 调节，这样 FOC 就会浪费多余的能量去纠正 d 轴，进而导致电机效率的降低。

我们根据这个实验仍可以看到，FOC 即使是在角度产生较大偏移的情况，q、d 轴的 PI 调节仍然将电机转速稳定到目标值，但是其代价电流升至 4A。

4.2.3 角度反向偏移情况

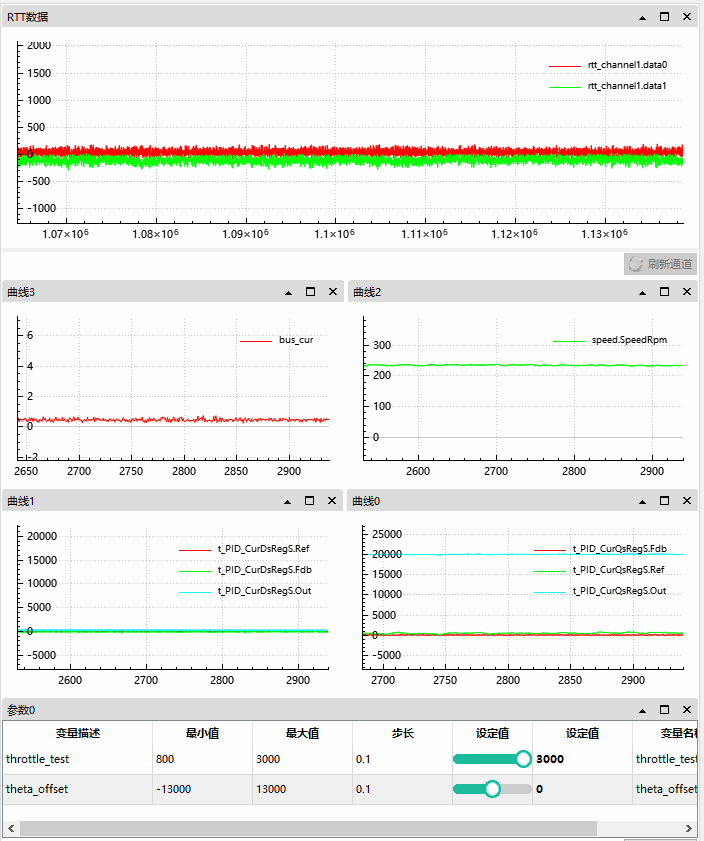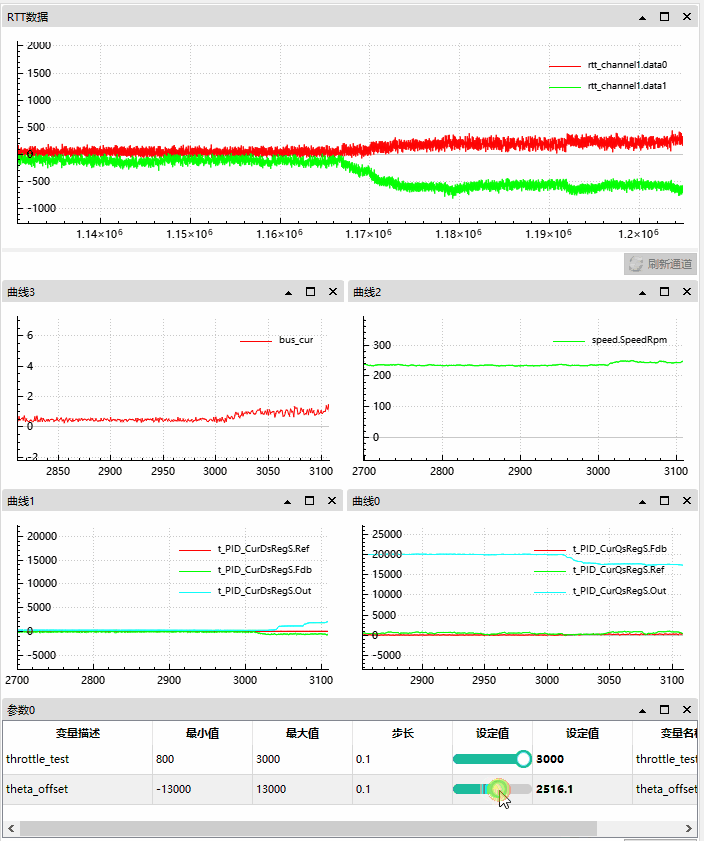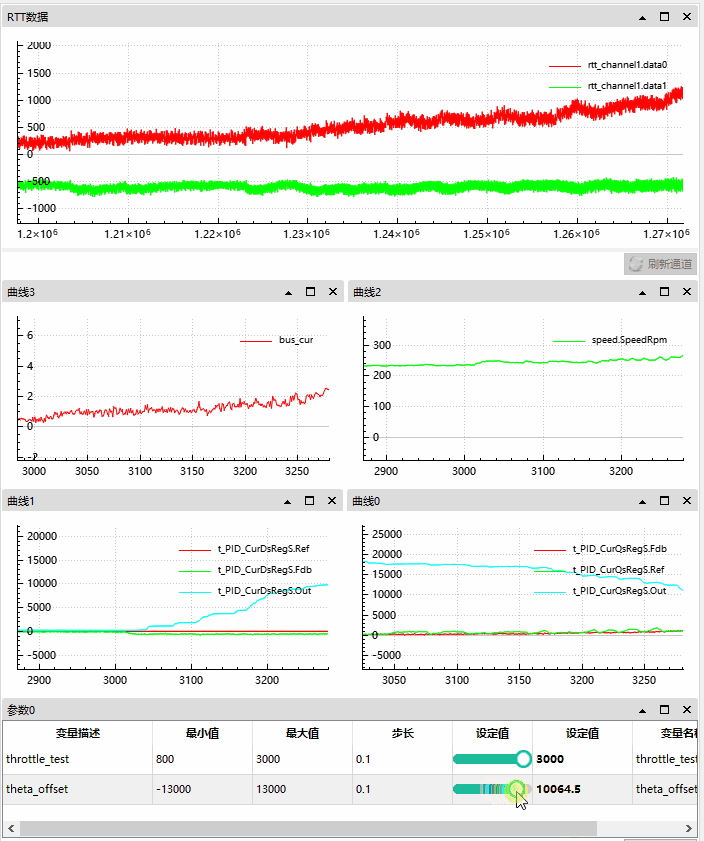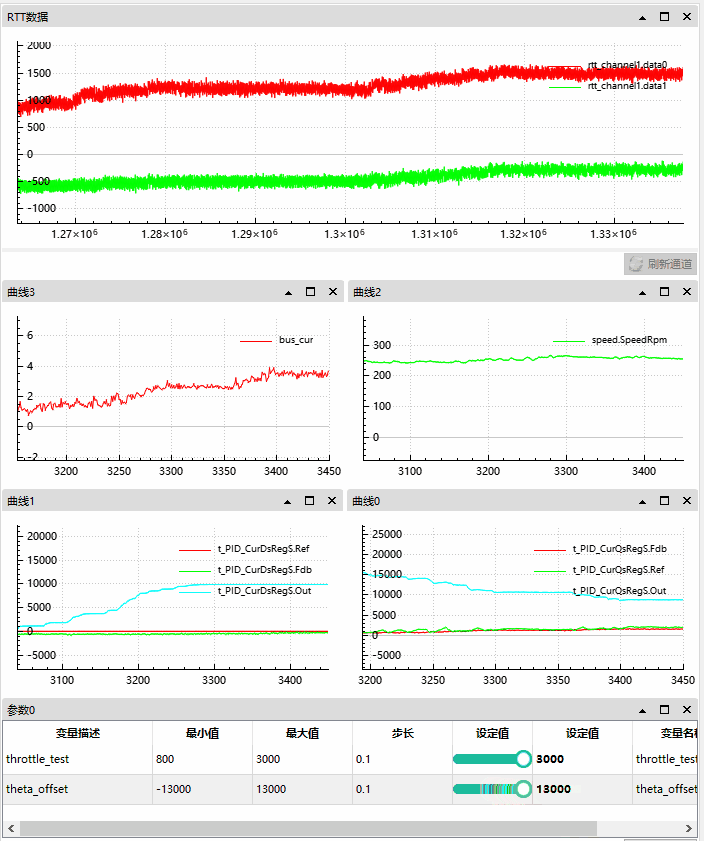
此时电机空转无负载。
我们可以观察到反向偏移越大，q 轴偏移越大，d 轴也是。
母线电流从 0.5A 升至 6A；
电机转速在 230 Rpm 后轻微下降；
角度偏移从 0 至 -12000；
d 轴目标为 0，反馈为负 -200 左右升至 2000 左右，输出逐渐减小，直到 -15000 最小值；
q 轴目标和反馈一起升高，输出最大 20000；

和角度正向偏移情况完全相反，比较有意思的地方是 d 轴输出到了我们人为设定最小值 -15000 之后，q、d 轴和母线电流急剧升高，说明 FOC框架的 PI 调节已经无法纠正这样的错误了。