当前位置：首页 > news >正文

【LeetCode热题100道笔记】二叉树展开为链表

news 2025/9/7 5:31:43

题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。

示例 1：
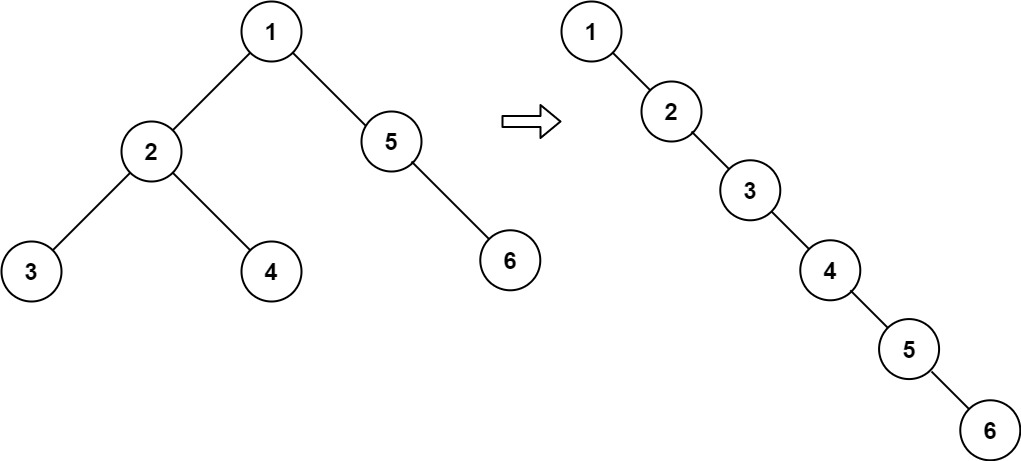
在这里插入图片描述
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [0]
输出：[0]

提示：
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

思考：前序遍历+左子树链表化

核心是递归处理左右子树：先将左、右子树分别展开为链表，再将左子树链表接到根节点的右指针，最后将原右子树链表接到左子树链表的尾部，实现“根→左子树链表→右子树链表”的前序顺序。

算法过程

递归终止条件：若当前节点为null（空树/叶子节点的子树），返回null（无需处理）。
递归展开子树：
- 递归展开左子树，得到左子树链表的头节点left；
- 递归展开右子树，得到右子树链表的头节点right。
重组当前节点的指针：
- 将当前节点的右指针指向左子树链表（root.right = left），左指针置为null（root.left = null）；
- 遍历左子树链表至尾部（找到最后一个节点），将其右指针指向右子树链表（current.right = right）。
返回当前节点：作为上层节点的左/右子树链表头，完成递归回溯。

时空复杂度

时间复杂度：O(n)，n为二叉树节点总数。
原因：每个节点仅被访问1次（递归处理），遍历左子树链表尾部的操作总次数为O(n)（每个节点最多被遍历1次），总时间与节点数线性相关。
空间复杂度：O(h)，h为二叉树高度。
原因：递归调用栈深度取决于树高，平衡树h=O(log n)，链状树h=O(n)；额外空间仅为递归栈，无其他存储开销。

代码（前序遍历版）

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {void} Do not return anything, modify root in-place instead.*/
var flatten = function(root) {preOrder(root);
};// 辅助函数：将以root为根的树展开为链表，返回展开后的头节点
function preOrder(root) {if (!root) return null; // 空节点直接返回// 递归展开左、右子树let left = preOrder(root.left);let right = preOrder(root.right);// 1. 将左子树链表接到根节点的右指针，左指针置空root.right = left;root.left = null;// 2. 找到左子树链表的尾部，将右子树链表接在其后let current = root;while (current.right) { // 遍历至左子树链表的最后一个节点current = current.right;}current.right = right;return root; // 返回当前节点作为上层的子树链表头
}

关键逻辑解析

为何用前序遍历？
题目要求展开后的链表顺序与前序遍历一致（根→左→右），前序遍历的递归顺序天然匹配这一需求：先处理根节点，再处理左子树，最后处理右子树，确保重组后的指针顺序正确。
左指针为何必须置空？
展开后的链表要求所有节点的左指针为null，仅保留右指针指向后续节点。若不置空左指针，会导致链表中残留左子树引用，破坏“链表”的结构定义。
如何高效找到左子树链表的尾部？
代码中通过while (current.right)循环遍历左子树链表至尾部，这是最直观的实现。对于极端情况（左子树为链状），该操作时间复杂度为O(k)（k为左子树节点数），但整棵树的总遍历次数仍为O(n)（每个节点最多被遍历1次），不影响整体时间复杂度。
是否可以优化空间复杂度？
上述递归实现的空间复杂度为O(h)，若需进一步优化至O(1)，可采用Morris遍历（线索化遍历），通过修改空指针临时指向前驱/后继节点，避免递归栈开销，但代码逻辑会更复杂。