状压 dp --- 棋盘覆盖问题

hello，大家好，今天是 2025 年 9 月 5 日，我们继续开启状压 dp 的学习。

今天我要来给大家介绍的是状压 dp 中的一类经典问题 --- 棋盘覆盖问题

和 TSP 问题一样，棋盘覆盖问题也很好识别，解决方式也相对固定。

一：棋盘覆盖问题简介

在这类问题中，一般针对的是一个二维棋盘：

需要在一些限定条件下，用棋子覆盖棋盘，最终求得所有合法方案的数目；

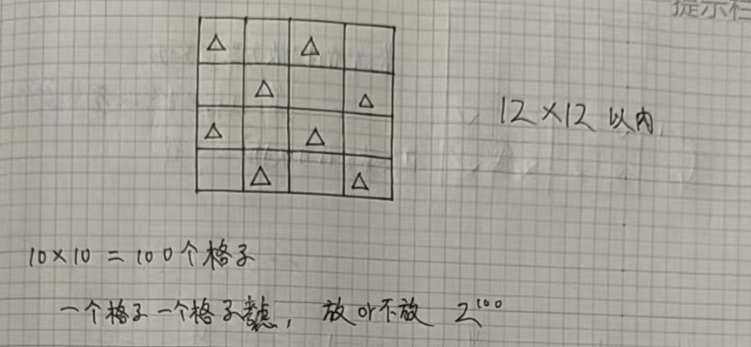
棋盘一般比较小，在 12 * 12 以内；（棋盘覆盖问题很好识别）

但是，暴搜的话一般会超时，因为总的方案数一般很大，通过暴搜枚举所有的方案会超时。

如果是 10 * 10 的棋盘，一个格子一个格子的考虑，针对每一个格子放或者不放，就有2^100种      情况。

二：棋盘覆盖问题模板题

题目一：互不侵犯

题目链接：互不侵犯

【题目描述】

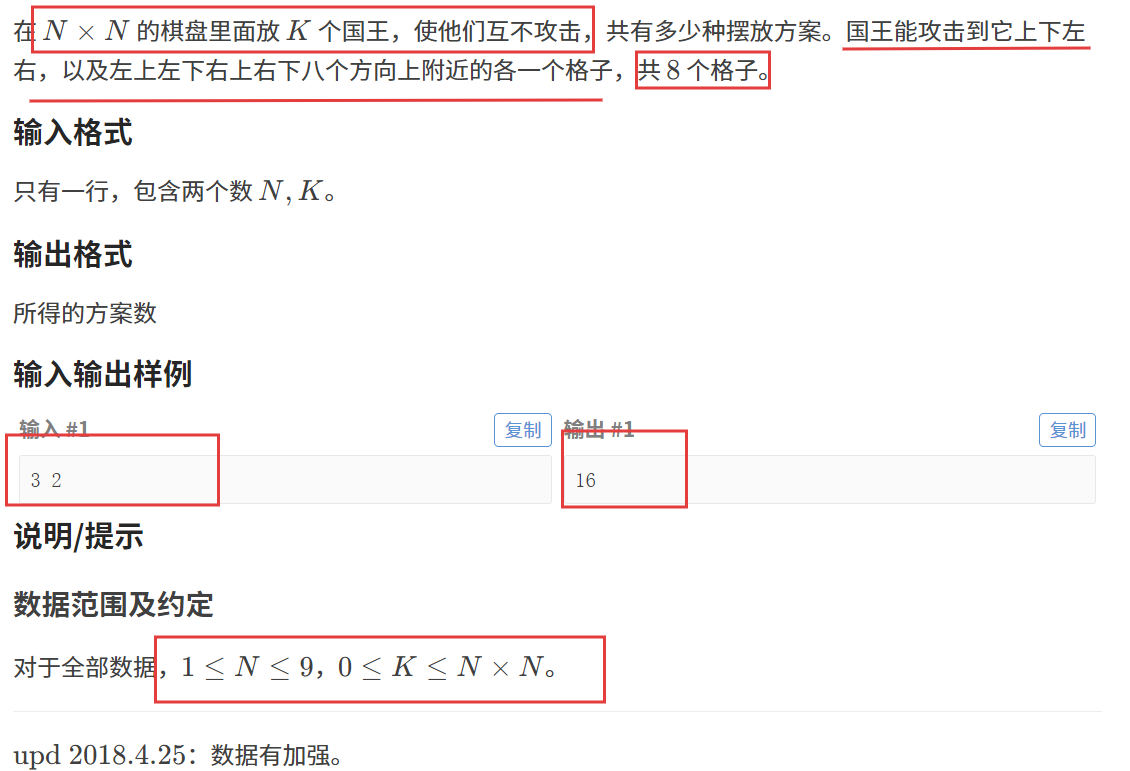
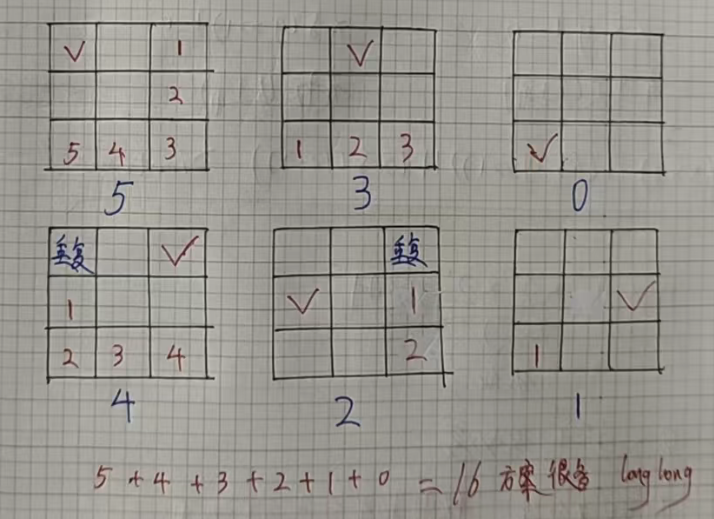
【算法原理】

通过模拟测试用例，我们发现，3 * 3 的棋盘放 2 个国王就会出现 16 种情况，因此，棋盘覆盖问题的结果可能会很大，我们要记得开 longlong。

我们不难发现一个性质：如果从上往下填写的是第 i 行，那么只会有第 i - 1 行会影响第 i 行的填写，因此，只要我们确定了第 i - 1 行的填写方式，就能得出第 i 行的填写方式。

我们考虑一下使用动态规划来解决这个问题：

状态压缩：我们把某一行的摆放方案用整数的二进制表示。

1.状态表示：

f[i][j][x]：表示：当前摆到了第 i 行，一共摆放了 j 个棋子，第 i 行的摆放方案为 x 时，所有的合法方案数。

2.状态转移方程：

我们根据最近的一步来划分问题：

假设第 i - 1 行的摆放方式为 y，c[x] 表示 x 的二进制表示中，一共有多少个 1。

状态转移方程成立的前提是，x 和 y 这两个状态不能冲突。那么如何保证这两行的摆放方式不会冲突呢？

我们结合位运算的知识就可以轻松搞定：

推到完状态转移方程之后，我们思考一下时间复杂度：

一共要遍历 n 行，最多要防止 n * n 个棋子，本行的放置方案有 2 ^ n 种，上一行的放置方案也有 2 ^ n 种，因此如果不做任何优化的话，时间复杂度为 O(n * n * n * 2 ^ n * 2 * n)，肯定是会超时的。

我们考虑一下优化，我们可以提前将每一行所有的合法方案全部预处理出来，这样的话最后就可以只枚举所有的合法方案了。

每一行的合法方案只需要保证和其余的国王左右互不相邻就可以了。

我们还是使用位运算的知识来预处理：

3.初始化：

由于本体是求方案数的模型，因此 f[0][0][0] = 1 即可。

4.填表顺序：

仅需保证 i 从小到大即可。

5.最终结果：

根据状态表示，以及题目要求，我们的最终结果为：第 n 行时所有 f 表中 j == k 的值相加。

【代码实现】

#include <iostream>
#include <vector>using namespace std;typedef long long LL;
const int N = 11;int n, k;
vector<int> st; // 存行的合法摆放方案
int c[1 << N]; // c[i] 表示：i 这个数的二进制表示中，1 的个数 
LL f[N][N * N][1 << N];int main()
{cin >> n >> k;// 预处理所有的合法方案，以及合法方案中 1 的个数for(int s = 0; s < (1 << n); s++){if(s & (s >> 1)) continue;st.push_back(s);for(int i = 0; i < n; i++)if((s >> i) & 1)c[s]++;} f[0][0][0] = 1;for(int i = 1; i <= n + 1; i++) // 枚举行 for(int j = 0; j <= k; j++) // 枚举棋子数目for(auto x : st) // 最后一行的方案for(auto y : st) // 上一行的方案{if((j < c[x]) || (x & y) || (x & (y >> 1)) || (x & (y << 1))) continue;f[i][j][x] += f[i - 1][j - c[x]][y];} //	LL ret = 0;
//	for(auto s : st) ret += f[n][k][s];
//	cout << ret << endl;cout << f[n + 1][k][0] << endl;return 0;
}

题目二：Corn Fields G

题目链接：Corn Fields G

本题是一道二倍经验的题目，算法原理和上一题基本类似。希望大家能够自己尝试解决之后，再去看下面的内容。

【题目描述】

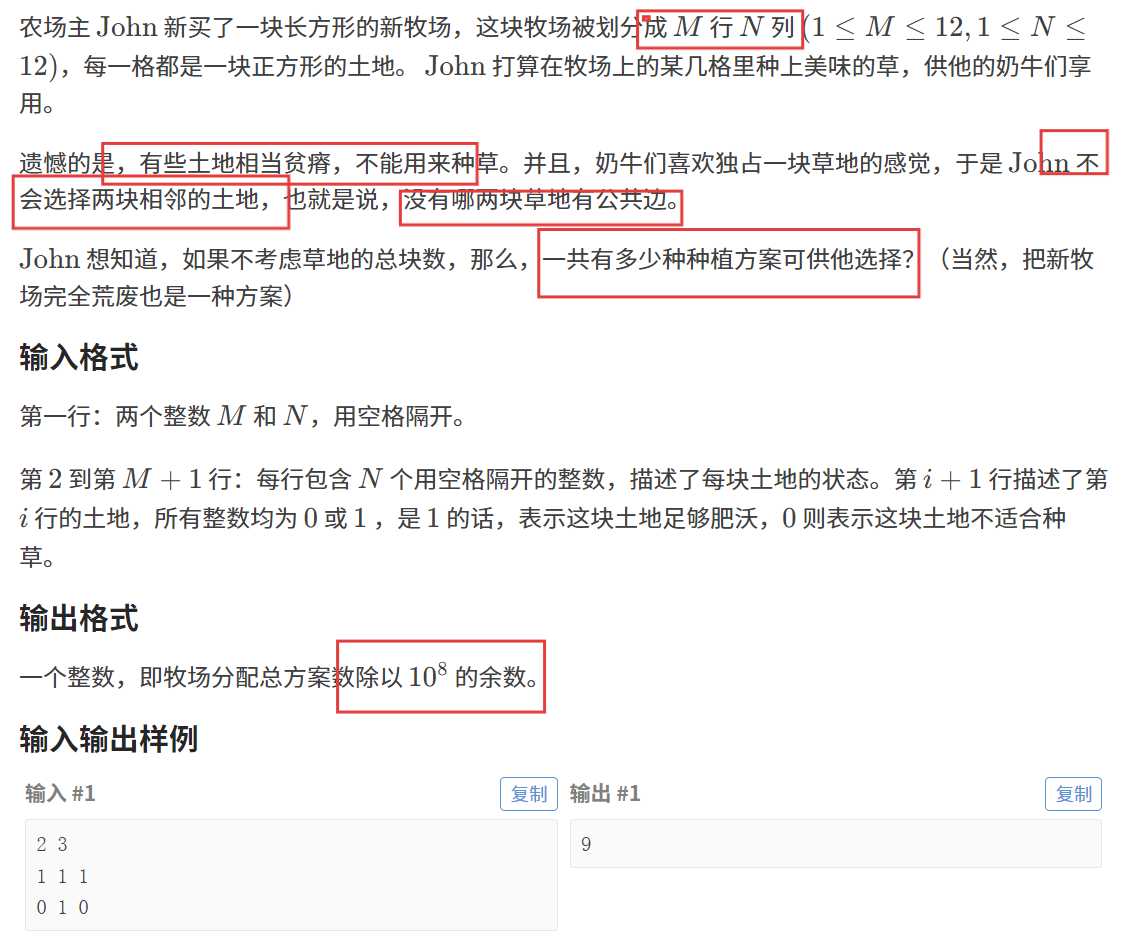
【算法原理】

解法：状压 dp

1.状态表示：

f[i][x]表示：第 i 行的摆放方案为 x 时，所有合法方案的总数。

2.状态转移方程：

假设第 i - 1 行的摆放方式为 y，当 x 和 y 不冲突时：

f[i][x] += f[i - 1][y]；

如何判断 x 和 y 是否冲突？？？

如果 x 和 y 执行按位与运算，最终结果等于 0，说明不冲突。最终结果不等于 0，说明会有冲突。

优化：我们可以提前预处理处每一行的合法方案：（考虑土地贫瘠情况）

接下来的三步和题目一类似，这里就不再多说了~~~

3. 初始化 f[0][0] = 1；

4. 填表顺序：保证 i 从大到小枚举即可。

5. 最终结果：根据状态表示，以及题目要求，最终结果为 f[n + 1][0]。

【代码实现】

#include <iostream>
#include <vector>using namespace std;typedef long long LL;
const int N = 14, mod = 1e8;int m, n;
vector<int> st[N];
int a[N];LL f[N][1 << N];int main()
{cin >> m >> n;for(int i = 1; i <= m; i++){for(int j = 0; j < n; j++){int x; cin >> x;if(x) a[i] |= (1 << j);}// 预处理当前这一行所有的合法状态for(int s = 0; s < (1 << n); s++){if((s & (s >> 1)) || ((s & a[i]) != s)) continue;st[i].push_back(s);} }f[0][0] = 1; st[0].push_back(0); st[m + 1].push_back(0);for(int i = 1; i <= m + 1; i++)for(int x : st[i])for(int y : st[i - 1]){if(x & y) continue;f[i][x] = (f[i][x] + f[i - 1][y]) % mod; }cout << f[m + 1][0] << endl;return 0;
}

好的，今天的分享就先到这里了，大家晚安！！！